SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Kun je die niet splitsen in de kansdichtheidsfunctie van X^2 en -X^2 voor resp. X >= 0 en X < 0?quote:Op maandag 8 december 2014 22:24 schreef thabit het volgende:
[..]
Dat is op zich waar, maar we zijn op zoek naar de kansdichtheidsfunctie van X|X|.


Een willekeurige functie. Convolutie met G staat overigens gelijk aan de Hilberttransformatie (dat is misschien ook wel handig om te vermelden).quote:


Je vergeet de factor 9.quote:Op dinsdag 9 december 2014 13:53 schreef PieterJanDeVakman het volgende:
[ afbeelding ]
Wat doe ik verkeerd 😡?
Volgens mijn GR is de uitkomst onjuist.
En je notatie is sloppy:


Lijkt me niet handig. Je wilt P(X|X|<=z) weten.quote:Op maandag 8 december 2014 22:26 schreef Amoeba het volgende:
[..]
Kun je die niet splitsen in de kansdichtheidsfunctie van X^2 en -X^2 voor resp. X >= 0 en X < 0?


Willekeurig? Dus geen voorwaarden op het domein, het codomein, continuďteit, etc?quote:Op maandag 8 december 2014 22:29 schreef defineaz het volgende:
[..]
Een willekeurige functie. Convolutie met G staat overigens gelijk aan de Hilberttransformatie (dat is misschien ook wel handig om te vermelden).


Stel je hebt twee marginale opbrengsten functies (per bedrijf 1, dus je hebt twee bedrijven):
MR1 = 30 - 2Q
en
MR2 = 12
Wat is dan de totale MR-functie? Ofwel de opgetelde MR-functie?
MR1 = 30 - 2Q
en
MR2 = 12
Wat is dan de totale MR-functie? Ofwel de opgetelde MR-functie?


42 - 2Q.
[spoiler]Eindelijk een vraag in dit topic waar ik 't antwoord op weet [/spoiler]
[/spoiler]
[ Bericht 33% gewijzigd door #ANONIEM op 09-12-2014 22:06:27 ]
[spoiler]Eindelijk een vraag in dit topic waar ik 't antwoord op weet
[ Bericht 33% gewijzigd door #ANONIEM op 09-12-2014 22:06:27 ]


quote:Op dinsdag 9 december 2014 21:08 schreef 2thmx het volgende:
42 - 2Q.Weet je dat zeker?SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.


quote:Op dinsdag 9 december 2014 21:08 schreef 2thmx het volgende:
42 - 2Q.In een plaatje in mijn boek heeft de lijn van de opgetelde MR curve in een bepaald punt een knik...SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.


Nee, eigenlijk nietquote:
Dus voor: MR = 12 --> TR =12Q --> P = 12.
Voor MR = 30 - 2Q --> TR = 30Q - Q^2 --> P = 30-Q
Dan heb je dus twee vraagfuncties:
P = 12 en P = 30 - Q
Die mag je horizontaal optellen, zie: https://www.khanacademy.o(...)adding-demand-curves
Dan krijg je voor 0<Q<18 de vraagcurve P = 30 - Q en voor Q > 18 de vraagcurve P = 12
De totale MR is dus MR = 30 - 2Q voor 0<Q<18 en MR = 12 voor Q > 18.
Vandaar dus de 'knik' in de totale MR-curve.
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
[ Bericht 1% gewijzigd door #ANONIEM op 09-12-2014 22:04:21 ]


Ik was inderdaad een beetje slordig: f is een Schwartz functie (hoewel dat in de opgave niet expliciet stond, en ik dat in eerste instantie ook niet door had, was het inderdaad een van de dingen waar je juist op moet letten bij dat vak: ik blijf het erg lastig vinden omdat het boek wat we gebruiken juist alleen hele losse schetsen van bewijzen geeft).quote:Op dinsdag 9 december 2014 21:00 schreef thabit het volgende:
[..]
Willekeurig? Dus geen voorwaarden op het domein, het codomein, continuďteit, etc?
Ik ben er trouwens (grotendeels) uitgekomen. Als je interesse hebt kan ik je wel de precieze opgave laten zien.


Bekijk:quote:Op woensdag 10 december 2014 20:22 schreef Goldenrush het volgende:
Waarom is 2log (x) = ln (x) / ln (2)
Het is een rekenregel, maar waarom?
We weten dat:
Dus:
Dit is van de vorm
Dus:
Nemen we nu aan beide kanten de natuurlijke logaritme:
Als we deze laatste gelijkheid omschrijven komen we uit op het resultaat:
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.


Je hebt een rekenregel voor het omzetten van een logaritme van een getal a met een basis ofwel grondtal b naar een logaritme met een basis ofwel grondtal g:quote:Op woensdag 10 december 2014 20:22 schreef Goldenrush het volgende:
Waarom is 2log (x) = ln (x) / ln (2)
Het is een rekenregel, maar waarom?
Deze regel kun je het gemakkelijkst onthouden in de zogeheten kettingvorm. Als je beide leden van deze identiteit met glog b vermenigvuldigt dan krijgen we:
en omgekeerd volgt de eerste identiteit uiteraard weer uit de tweede door beide leden te delen door glog b. Merk op dat glog b hier ongelijk is aan 0 aangezien b hier tevens het grondtal is van een logaritme en b dus een positief reëel getal is ongelijk aan 1 zodat glog b ≠ 0.
Het bewijs van deze regel is heel eenvoudig, dit volgt namelijk direct uit de definitie van de logaritme. Per definitie is glog b de exponent waartoe we g moeten verheffen om b te krijgen en is blog a de exponent waartoe we b moeten verheffen om a te krijgen. Stellen we dus
en
dan is
en
Maar omdat b = gx kunnen we voor dit laatste schrijven
en dus hebben we
Maar als het zo is dat we g tot de macht xy moeten verheffen om a te verkrijgen dan is dus, wederom volgens de definitie van de logaritme,
en omdat x = glog b en y = blog a hebben we dus inderdaad
QED
Als het grondtal g van een logaritme gelijk is aan het bijzondere getal e, dan spreken we van de natuurlijke logaritme (logarithmus naturalis) en schrijven we gewoonlijk ln x voor elog x. Bovenstaande identiteit
wordt dan


Helder, heel erg bedankt!quote:Op woensdag 10 december 2014 21:50 schreef Riparius het volgende:
[..]
Je hebt een rekenregel voor het omzetten van een logaritme van een getal a met een basis ofwel grondtal b naar een logaritme met een basis ofwel grondtal g:
Deze regel kun je het gemakkelijkst onthouden in de zogeheten kettingvorm. Als je beide leden van deze identiteit met glog b vermenigvuldigt dan krijgen we:
en omgekeerd volgt de eerste identiteit uiteraard weer uit de tweede door beide leden te delen door glog b. Merk op dat glog b hier ongelijk is aan 0 aangezien b hier tevens het grondtal is van een logaritme en b dus een positief reëel getal is ongelijk aan 1 zodat glog b ≠ 0.
Het bewijs van deze regel is heel eenvoudig, dit volgt namelijk direct uit de definitie van de logaritme. Per definitie is glog b de exponent waartoe we g moeten verheffen om b te krijgen en is blog a de exponent waartoe we b moeten verheffen om a te krijgen. Stellen we dus
en
dan is
en
Maar omdat b = gx kunnen we voor dit laatste schrijven
en dus hebben we
Maar als het zo is dat we g tot de macht xy moeten verheffen om a te verkrijgen dan is dus, wederom volgens de definitie van de logaritme,
en omdat x = glog b en y = blog a hebben we dus inderdaad
QED
Als het grondtal g van een logaritme gelijk is aan het bijzondere getal e, dan spreken we van de natuurlijke logaritme (logarithmus naturalis) en schrijven we gewoonlijk ln x voor elog x. Bovenstaande identiteit
wordt dan


Wordt het nog geen tijd voor een [Economie] Huiswerk- en vragentopic?
Opinion is the medium between knowledge and ignorance (Plato)


In principe is dit ook wiskunde toch..?quote:Op donderdag 11 december 2014 17:38 schreef Janneke141 het volgende:
Wordt het nog geen tijd voor een [Economie] Huiswerk- en vragentopic?


Het is niet direct mijn insteek om een definitiediscussie te starten, maar volgens mij is een aantal vragen die jij en nog wat andere users posten niet te beantwoorden zonder de benodigde kennis van een aantal economische termen, zoals in dit geval nutsfuncties en perfecte substituten.quote:Op donderdag 11 december 2014 17:39 schreef RustCohle het volgende:
[..]
In principe is dit ook wiskunde toch..?
[ Bericht 0% gewijzigd door Janneke141 op 11-12-2014 17:53:32 ]
Opinion is the medium between knowledge and ignorance (Plato)


Ik zal eens een poging wagen om een economie topic te openen.quote:Op donderdag 11 december 2014 17:42 schreef Janneke141 het volgende:
[..]
Het is niet direct mijn insteek om een definitiediscussie te starten, maar volgens mij zijn een aantal vragen die jij en nog wat andere users posten niet te beantwoorden zonder de benodigde kennis van een aantal economische termen, zoals in dit geval nutsfuncties en perfecte substituten.


Als jij de vraag wiskundig kan formuleren, kunnem we hem misschien beantwoorden.quote:Op donderdag 11 december 2014 17:36 schreef RustCohle het volgende:
[ afbeelding ]
Hoe kan ik erachter komen of A en B perfecte substituten van elkaar zijn?


Goedenavond,
Kan iemand mij helpen met het oplossen van de volgende functie voor x?:
Px X + [ a/(1-a) ] Px X = M
Px is iets anders dan X...
Volledige opgave:
En dan oplossen voor X..
Kan iemand mij helpen met het oplossen van de volgende functie voor x?:
Px X + [ a/(1-a) ] Px X = M
Px is iets anders dan X...
Volledige opgave:
En dan oplossen voor X..


Een functie kan je niet oplossen.quote:Op donderdag 11 december 2014 20:21 schreef Super-B het volgende:
Kan iemand mij helpen met het oplossen van de volgende functie voor x?:
Bovendien zie je twee vergelijkingen met een stuk of vijf onbekenden, dus 'oplossen' zou ook in het geval van de correcte formulering (geef een oplossing voor dit stelsel van vergelijkingen) niet lukken.
Wat is de bedoeling van de opgave, dat je een uitdrukking geeft van de vorm X = ...? En zo ja, uitgedrukt in wat? Y, M, ..?
Opinion is the medium between knowledge and ignorance (Plato)


Laat ze lekker het voorgeschreven boek doorlezen, daar staat het allemaal (beknopt) uitgelegd. Maar nee, gasten willen een voorgekauwd antwoord, ja daar heb je wat aan.quote:Op donderdag 11 december 2014 17:42 schreef Janneke141 het volgende:
[..]
Het is niet direct mijn insteek om een definitiediscussie te starten, maar volgens mij is een aantal vragen die jij en nog wat andere users posten niet te beantwoorden zonder de benodigde kennis van een aantal economische termen, zoals in dit geval nutsfuncties en perfecte substituten.
Onoverwinnelijk/Rotterdam/Zeerover
https://www.playgwent.com/en/ - Official beta of Gwent: The Witcher Gard Game
https://www.playgwent.com/en/ - Official beta of Gwent: The Witcher Gard Game


Ik snap de essentie van alles, maar er staat in twee termen een Px en dat brengt mij in de war.quote:Op donderdag 11 december 2014 20:33 schreef CapnIzzy het volgende:
[..]
Laat ze lekker het voorgeschreven boek doorlezen, daar staat het allemaal (beknopt) uitgelegd. Maar nee, gasten willen een voorgekauwd antwoord, ja daar heb je wat aan.


Uitgedrukt van de vorm X = ... inderdaad. Dat maakt niet uit, zolang het maar van de vorm X = ... is.quote:Op donderdag 11 december 2014 20:29 schreef Janneke141 het volgende:
[..]
Een functie kan je niet oplossen.
Bovendien zie je twee vergelijkingen met een stuk of vijf onbekenden, dus 'oplossen' zou ook in het geval van de correcte formulering (geef een oplossing voor dit stelsel van vergelijkingen) niet lukken.
Wat is de bedoeling van de opgave, dat je een uitdrukking geeft van de vorm X = ...? En zo ja, uitgedrukt in wat? Y, M, ..?


Nou, dan zou ik gaan voor X = (M-Y)/pX. Lange halen, snel thuis.quote:Op donderdag 11 december 2014 20:45 schreef Super-B het volgende:
[..]
Uitgedrukt van de vorm X = ... inderdaad. Dat maakt niet uit, zolang het maar van de vorm X = ... is.
Opinion is the medium between knowledge and ignorance (Plato)


Het moet zijn..quote:Op donderdag 11 december 2014 20:47 schreef Janneke141 het volgende:
[..]
Nou, dan zou ik gaan voor X = (M-Y)/pX. Lange halen, snel thuis.
Ik had het volgende:
Px X + [ a/(1-a) ] Px X = m
Px X ( 1 + [ a/(1-a) ] ) = m
X = M / ( 1 + [ a/(1-a) ] * Px)


Misschien anders het standaard advies van Dhr. Spliet opvolgenquote:Op donderdag 11 december 2014 20:44 schreef Super-B het volgende:
[..]
Ik snap de essentie van alles, maar er staat in twee termen een Px en dat brengt mij in de war.
Onoverwinnelijk/Rotterdam/Zeerover
https://www.playgwent.com/en/ - Official beta of Gwent: The Witcher Gard Game
https://www.playgwent.com/en/ - Official beta of Gwent: The Witcher Gard Game


Er een nachtje over slapen uiteraardquote:
Onoverwinnelijk/Rotterdam/Zeerover
https://www.playgwent.com/en/ - Official beta of Gwent: The Witcher Gard Game
https://www.playgwent.com/en/ - Official beta of Gwent: The Witcher Gard Game


Ja, dat kan ook. Maar die van mij kan ook, aangezien het volgens jou niet uitmaakte hoe het eruit zag.quote:
Je bent op weg.quote:Ik had het volgende:
Px X + [ a/(1-a) ] Px X = m
Px X ( 1 + [ a/(1-a) ] ) = m
X = M / ( 1 + [ a/(1-a) ] * Px)
Bedenk dat 1 + a/(1-a) = (1-a)/(1-a) + a/(1-a) = (1-a+a)/(1-a), en dan kom je er wel uit verder.
Opinion is the medium between knowledge and ignorance (Plato)


Die van jou is ook erg handig, met name omdat het zorgt dat de kans dat ik een fout maak kleiner wordt.. Op het moment wanneer het in de vorm van X =... is geschreven is het een kwestie van de Y te vervangen door de variabelen..quote:Op donderdag 11 december 2014 20:52 schreef Janneke141 het volgende:
[..]
Ja, dat kan ook. Maar die van mij kan ook, aangezien het volgens jou niet uitmaakte hoe het eruit zag.
[..]
Je bent op weg.
Bedenk dat 1 + a/(1-a) = (1-a)/(1-a) + a/(1-a) = (1-a+a)/(1-a), en dan kom je er wel uit verder.
Even het vetgedrukte opschrijven...


1 -aquote:Op donderdag 11 december 2014 20:52 schreef Janneke141 het volgende:
[..]
Ja, dat kan ook. Maar die van mij kan ook, aangezien het volgens jou niet uitmaakte hoe het eruit zag.
[..]
Je bent op weg.
Bedenk dat 1 + a/(1-a) = (1-a)/(1-a) + a/(1-a) = (1-a+a)/(1-a), en dan kom je er wel uit verder.
Ben er uit! Top bedankt. Ik ga het even op jouw manier proberen nu... --> Y laten staan zoals het is en het later invullen..quote:Op donderdag 11 december 2014 20:52 schreef Janneke141 het volgende:
[..]
Ja, dat kan ook. Maar die van mij kan ook, aangezien het volgens jou niet uitmaakte hoe het eruit zag.
[..]
Je bent op weg.
Bedenk dat 1 + a/(1-a) = (1-a)/(1-a) + a/(1-a) = (1-a+a)/(1-a), en dan kom je er wel uit verder.


Iemand enig idee wat een cirkel in positieve zin doorlopen precies betekend?
[ afbeelding ]
Ik dacht zelf aan eerst de grote cirkel doorlopen tegen de wijzers van de klok in van x=3 tot x=-3 en dan de kleine cirkel doorlopen van x=-1 tot x=1 met de wijzers van de klok mee, maar hiermee kom ik niet tot het goede antwoord als ik het vectorveld integreer over het ingesloten oppervlak.
[ afbeelding ]
Ik dacht zelf aan eerst de grote cirkel doorlopen tegen de wijzers van de klok in van x=3 tot x=-3 en dan de kleine cirkel doorlopen van x=-1 tot x=1 met de wijzers van de klok mee, maar hiermee kom ik niet tot het goede antwoord als ik het vectorveld integreer over het ingesloten oppervlak.


Positief is inderdaad tegen de klok in en negatief met de klok mee.quote:Op vrijdag 12 december 2014 19:12 schreef spacer730 het volgende:
Iemand enig idee wat een cirkel in positieve zin doorlopen precies betekend?
[ afbeelding ]
Ik dacht zelf aan eerst de grote cirkel doorlopen tegen de wijzers van de klok in van x=3 tot x=-3 en dan de kleine cirkel doorlopen van x=-1 tot x=1 met de wijzers van de klok mee, maar hiermee kom ik niet tot het goede antwoord als ik het vectorveld integreer over het ingesloten oppervlak.
Kan je de berekening eens laten zien?
-edit- Oh wacht ben jij niet halve cirkels aan het doorlopen?


Ja ik was bij mijn vorige berekening halve cirkels aan het doorlopen, omdat ik dacht dat K een enkelvoudig gesloten kromme is. Dit is volgens mij niet de bedoeling, maar wat dan wel? Integreren over het gebied tussen de cirkels met straal 3 en 1?quote:Op vrijdag 12 december 2014 19:19 schreef t4rt4rus het volgende:
[..]
Positief is inderdaad tegen de klok in en negatief met de klok mee.
Kan je de berekening eens laten zien?
-edit- Oh wacht ben jij niet halve cirkels aan het doorlopen?


Wat jij doet is niet de bedoeling. Je moet de complete cirkel met radius 3 doorlopen in tegenwijzerzin en tevens de complete cirkel met radius 1 doorlopen in wijzerzin.quote:Op vrijdag 12 december 2014 19:12 schreef spacer730 het volgende:
Iemand enig idee wat een cirkel in positieve zin doorlopen precies betekent?
[ afbeelding ]
Ik dacht zelf aan eerst de grote cirkel doorlopen tegen de wijzers van de klok in van x=3 tot x=-3 en dan de kleine cirkel doorlopen van x=-1 tot x=1 met de wijzers van de klok mee, maar hiermee kom ik niet tot het goede antwoord als ik het vectorveld integreer over het ingesloten oppervlak.


Gewoon over beide cirkels integreren.quote:Op vrijdag 12 december 2014 19:25 schreef spacer730 het volgende:
[..]
Ja ik was bij mijn vorige berekening halve cirkels aan het doorlopen, omdat ik dacht dat K een enkelvoudig gesloten kromme is. Dit is volgens mij niet de bedoeling, maar wat dan wel? Integreren over het gebied tussen de cirkels met straal 3 en 1?
-edit- oh Riparius had al gereageerd.


quote:Op vrijdag 12 december 2014 19:27 schreef Riparius het volgende:
[..]
Wat jij doet is niet de bedoeling. Je moet de complete cirkel met radius 3 doorlopen in tegenwijzerzin en tevens de complete cirkel met radius 1 doorlopen in wijzerzin.
Bedankt voor de hulp, hij is nu gelukt. Ik besefte niet dat je hier dus eigenlijk 2x de stelling van green moet toepassenquote:Op vrijdag 12 december 2014 19:27 schreef t4rt4rus het volgende:
[..]
Gewoon over beide cirkels integreren.
-edit- oh Riparius had al gereageerd.


Je hoeft dus alleen maar te integreren over de shell.quote:Op vrijdag 12 december 2014 19:45 schreef spacer730 het volgende:
[..]
[..]
Bedankt voor de hulp, hij is nu gelukt. Ik besefte niet dat je hier dus eigenlijk 2x de stelling van green moet toepassen


Kan iemand mij helpen met kansrekenen?
''Stel je bent op zoek naar een lage prijs op een prijsdistributie dat uniform is verdeeld op het interval (1,2). Wat is je acceptabele prijs als de kosten voor het zoeken 0,10 euro zijn?''
Ik had een tekening gemaakt:
Met de volgende berekening:
Kans * (gemiddelde) opbrengst:
[ (p-1) / 2 ] * [ (p-1) / 2 ] = 0,10
(p-1)˛ / 4 = 0,10
(p-1)˛ = 0.4
p - 1 = 0.632
p= 1,632
Het antwoord daarentegen is 1,447
Antwoordenmodel:
''Stel je bent op zoek naar een lage prijs op een prijsdistributie dat uniform is verdeeld op het interval (1,2). Wat is je acceptabele prijs als de kosten voor het zoeken 0,10 euro zijn?''
Ik had een tekening gemaakt:
Met de volgende berekening:
Kans * (gemiddelde) opbrengst:
[ (p-1) / 2 ] * [ (p-1) / 2 ] = 0,10
(p-1)˛ / 4 = 0,10
(p-1)˛ = 0.4
p - 1 = 0.632
p= 1,632
Het antwoord daarentegen is 1,447
Antwoordenmodel:
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.


quote:Op zaterdag 13 december 2014 15:43 schreef Andijvie_ het volgende:
Kan iemand mij helpen met kansrekenen?
''Stel je bent op zoek naar een lage prijs op een prijsdistributie dat uniform is verdeeld op het interval (1,2). Wat is je acceptabele prijs als de kosten voor het zoeken 0,10 euro zijn?''
Ik had een tekening gemaakt:
[ afbeelding ]
Met de volgende berekening:
Kans * (gemiddelde) opbrengst:
[ (p-1) / 2 ] * [ (p-1) / 2 ] = 0,10
(p-1)˛ / 4 = 0,10
(p-1)˛ = 0.4
p - 1 = 0.632
p= 1,632
Het antwoord daarentegen is 1,447
Antwoordenmodel:Zoekmodel staat gewoon duidelijk toegelicht in de slides (paar jaar geleden in ieder geval).SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Onoverwinnelijk/Rotterdam/Zeerover
https://www.playgwent.com/en/ - Official beta of Gwent: The Witcher Gard Game


Nein.quote:Op zaterdag 13 december 2014 20:21 schreef CapnIzzy het volgende:
[..]
Zoekmodel staat gewoon duidelijk toegelicht in de slides (paar jaar geleden in ieder geval).


Ik heb een fout/error van een systeem 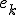 . Ik kan in principe alle momenten berekenen van de error
. Ik kan in principe alle momenten berekenen van de error 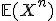 , het eerste moment
, het eerste moment 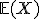 is natuurlijk de verwachte waarde. Ik kan dus ook de centrale momenten berekenen
is natuurlijk de verwachte waarde. Ik kan dus ook de centrale momenten berekenen 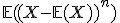 .De tweede centrale moment
.De tweede centrale moment 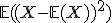 is de variantie.
is de variantie.
Nu zijn 2 performance criteria de moving average (voortschrijdend gemiddelde) en de moving standard deviation (voortschrijdend standaardafwijking) van de error, deze zijn gedefinieerd als volgt.
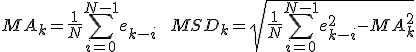
MA, geeft dus niet meer en minder aan dan de gemiddelde fout over een bepaalde lengte N en de MSD geeft de afwijking aan van de echte fout t.o.v. de gemiddelde fout.
Gezien ik de verwachte waarde van de error kan berekenen,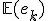 , en de variatie,
, en de variatie, 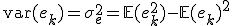 . Kan ik ook de verwachte waarde berekenen van de moving average
. Kan ik ook de verwachte waarde berekenen van de moving average
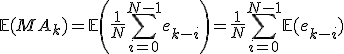
en een band daarom heen m.b.v. de standaard afwijking.
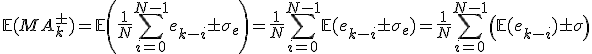
Nu wil ik ook de verwachte waarde van de moving standard deviation en de variatie daarvan berekenen of op zijn minst de standaard afwijking ervan zodat ik net zoals wat ik nu bij de moving average kan doen, de verwachte waarde daarvan berekenen plus/minus een bepaalde band daarom heen.
Is dit mogelijk? (Ik kan dus hogere orde momenten berekenen, weet niet of dat nuttig is maar meld het nog maar even :p)
Want in feite wil ik dus de standaard afwijking van de standaard afwijking weten? M.a.w. de variatie van de variatie? (Weet niet zeker of deze 2 statements correct zijn).
Nu zijn 2 performance criteria de moving average (voortschrijdend gemiddelde) en de moving standard deviation (voortschrijdend standaardafwijking) van de error, deze zijn gedefinieerd als volgt.
MA, geeft dus niet meer en minder aan dan de gemiddelde fout over een bepaalde lengte N en de MSD geeft de afwijking aan van de echte fout t.o.v. de gemiddelde fout.
Gezien ik de verwachte waarde van de error kan berekenen,
en een band daarom heen m.b.v. de standaard afwijking.
Nu wil ik ook de verwachte waarde van de moving standard deviation en de variatie daarvan berekenen of op zijn minst de standaard afwijking ervan zodat ik net zoals wat ik nu bij de moving average kan doen, de verwachte waarde daarvan berekenen plus/minus een bepaalde band daarom heen.
Is dit mogelijk? (Ik kan dus hogere orde momenten berekenen, weet niet of dat nuttig is maar meld het nog maar even :p)
Want in feite wil ik dus de standaard afwijking van de standaard afwijking weten? M.a.w. de variatie van de variatie? (Weet niet zeker of deze 2 statements correct zijn).


Er zijn wel wat ouderejaars econometristen op dit forum, misschien kan je hen even aanspreken. Of een willekeurige prof emailen die veel met tijdreeksen doet.quote:Op zondag 14 december 2014 16:38 schreef Dale. het volgende:
Ik heb een fout/error van een systeem. Ik kan in principe alle momenten berekenen van de error
, het eerste moment
is natuurlijk de verwachte waarde. Ik kan dus ook de centrale momenten berekenen
.De tweede centrale moment
is de variantie.
Nu zijn 2 performance criteria de moving average (voortschrijdend gemiddelde) en de moving standard deviation (voortschrijdend standaardafwijking) van de error, deze zijn gedefinieerd als volgt.
MA, geeft dus niet meer en minder aan dan de gemiddelde fout over een bepaalde lengte N en de MSD geeft de afwijking aan van de echte fout t.o.v. de gemiddelde fout.
Gezien ik de verwachte waarde van de error kan berekenen,, en de variatie,
. Kan ik ook de verwachte waarde berekenen van de moving average
en een band daarom heen m.b.v. de standaard afwijking.
Nu wil ik ook de verwachte waarde van de moving standard deviation en de variatie daarvan berekenen of op zijn minst de standaard afwijking ervan zodat ik net zoals wat ik nu bij de moving average kan doen, de verwachte waarde daarvan berekenen plus/minus een bepaalde band daarom heen.
Is dit mogelijk? (Ik kan dus hogere orde momenten berekenen, weet niet of dat nuttig is maar meld het nog maar even :p)
Want in feite wil ik dus de standaard afwijking van de standaard afwijking weten? M.a.w. de variatie van de variatie? (Weet niet zeker of deze 2 statements correct zijn).
Verder is de variatie van de variatie per definitie 0, dus volgens mij bedoel je wat anders.


Ik zit in de knoop met de volgende opgave:
Beschouw de verzameling V gegeven door de rijen (xn)n≥1
(termen in R) die voldoen aan de differentievergelijking xn+1 = xn + xn−1 voor
n ≥ 2.
1. Schrijf de eerste vijf termen op van de rij beginnend met (0, 1, . . .).
2. Schrijf de eerste vijf termen op van de rij beginnend met (1, 0, . . .).
3. Laat zien dat met de voor de hand liggende optelling en scalaire vermenigvuldiging
V een vectorruimte is van dimensie 2.
4. Stel η = (1 + √5)/2 en η′ = (1 −√5)/2. Laat zien dat de rijen (ηn)n≥1en (η′n)n≥1 voldoen aan de differentievergelijking.
5. Zij (un)n≥1 de oplossing van de differentievergelijking met begintermen 0,1. Dit is de rij van Fibonacci. Geef een formule voor un in termen van ηn en η′n.
Nu gaat het hoofdstuk over vectorruimten. Het hoofdstuk heb ik goed (proberen) door te nemen en te begrijpen, maar begrijp ik vrij weinig van wat ze precies in deze opgaven willen zien. Wat wordt er bedoeld met de 'rij beginnend met..'? Ik zie dit namelijk voor het eerst. Hebben jullie toevallig nog wat sites met info waarmee ik deze opgave zou kunnen oplossen? Het hoofdstuk in mijn boek staat namelijk vol met definities en bewijzen die mij niet bepaald verder helpen
[ Bericht 1% gewijzigd door Knuck-les op 14-12-2014 17:26:17 ]
Beschouw de verzameling V gegeven door de rijen (xn)n≥1
(termen in R) die voldoen aan de differentievergelijking xn+1 = xn + xn−1 voor
n ≥ 2.
1. Schrijf de eerste vijf termen op van de rij beginnend met (0, 1, . . .).
2. Schrijf de eerste vijf termen op van de rij beginnend met (1, 0, . . .).
3. Laat zien dat met de voor de hand liggende optelling en scalaire vermenigvuldiging
V een vectorruimte is van dimensie 2.
4. Stel η = (1 + √5)/2 en η′ = (1 −√5)/2. Laat zien dat de rijen (ηn)n≥1en (η′n)n≥1 voldoen aan de differentievergelijking.
5. Zij (un)n≥1 de oplossing van de differentievergelijking met begintermen 0,1. Dit is de rij van Fibonacci. Geef een formule voor un in termen van ηn en η′n.
Nu gaat het hoofdstuk over vectorruimten. Het hoofdstuk heb ik goed (proberen) door te nemen en te begrijpen, maar begrijp ik vrij weinig van wat ze precies in deze opgaven willen zien. Wat wordt er bedoeld met de 'rij beginnend met..'? Ik zie dit namelijk voor het eerst. Hebben jullie toevallig nog wat sites met info waarmee ik deze opgave zou kunnen oplossen? Het hoofdstuk in mijn boek staat namelijk vol met definities en bewijzen die mij niet bepaald verder helpen
[ Bericht 1% gewijzigd door Knuck-les op 14-12-2014 17:26:17 ]


Rij beginnend met (0,1,...) bedoelen ze mee x1 = 0 en x2 = 1.
Je hebt de eerste twee waardes nodig om de rest uit te kunnen rekenen.
Je hebt de eerste twee waardes nodig om de rest uit te kunnen rekenen.


Wat zie je als x1 en x2? Ik snap volgens mij ook niet echt hoe een differentievergelijking in elkaar zit. Zou je de eerste wellicht (deels) voor kunnen doen?quote:Op zondag 14 december 2014 17:38 schreef Anoonumos het volgende:
Rij beginnend met (0,1,...) bedoelen ze mee x1 = 0 en x2 = 1.
Je hebt de eerste twee waardes nodig om de rest uit te kunnen rekenen.
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |

 Op
Op 




