SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Nog één vraagje hoor:quote:Op dinsdag 21 oktober 2014 12:22 schreef Janneke141 het volgende:
[..]
Zie edit. Ik keek zelf even verkeerd, maar je afleiding klopt.
Volgens mij is de teller van f'xx altijd negatief, evenals de teller van f'yy. Bovendien zijn van beide (tweede ) afgeleide functies de hele breuk altijd positief. Dus hoe kan het zowel concaaf als convex zijn op het domein...? Volgens mij kan het alleen maar convex zijn...
x2y2 - 1 = (xy+1)(xy-1).quote:
[..]
Nog één vraagje hoor:
[ afbeelding ]
[ afbeelding ]
[ afbeelding ]
Volgens mij is de teller van f'xx altijd negatief, evenals de teller van f'yy. Bovendien zijn van beide (tweede ) afgeleide functies de hele breuk altijd positief. Dus hoe kan het zowel concaaf als convex zijn op het domein...? Volgens mij kan het alleen maar convex zijn...
Aangezien (xy+1) altijd positief is, en (xy-1) zowel positief als negatief kan zijn*, kan de teller van de uitdrukking positief of negatief zijn. De noemer is uiteraard altijd positief.
* Uiteraard onder de hier geldende voorwaarde xy>-1.
Opinion is the medium between knowledge and ignorance (Plato)
quote:
[..]
x2y2 - 1 = (xy+1)(xy-1).
Aangezien (xy+1) altijd positief is, en (xy-1) zowel positief als negatief kan zijn*, kan de teller van de uitdrukking positief of negatief zijn. De noemer is uiteraard altijd positief.
* Uiteraard onder de hier geldende voorwaarde xy>-1.
Volgens mij is de teller van f'xx altijd negatief, evenals de teller van f'yy. Bovendien zijn van beide (tweede ) afgeleide functies de hele breuk altijd positief. Dus hoe kan het zowel concaaf als convex zijn op het domein...? Volgens mij kan het alleen maar convex zijn...
En om concaaf te kunnen zijn moet f'xx en f'yy ook <0 zijn, maar het is altijd > 0 in tegenstelling tot f''xx * f''yy - (f''xy)²
Lees nog eens goed wat er staat in het plaatje dat je post:quote:
[..]
[ afbeelding ]
Volgens mij is de teller van f'xx altijd negatief, evenals de teller van f'yy. Bovendien zijn van beide (tweede ) afgeleide functies de hele breuk altijd positief. Dus hoe kan het zowel concaaf als convex zijn op het domein...? Volgens mij kan het alleen maar convex zijn...
En om concaaf te kunnen zijn moet f'xx en f'yy ook <0 zijn, maar het is altijd > 0 in tegenstelling tot f''xx * f''yy - (f''xy)²
We kunnen dus niet concluderen op basis van de voldoende voorwaarden dat de functie convex of concaaf is.
Er wordt dus niet gezegd dat het het een of het ander is, er wordt gezegd dat het beide niet aantoonbaar is. En die bewering klopt.
Opinion is the medium between knowledge and ignorance (Plato)
ohhh ok thanks.quote:
[..]
Lees nog eens goed wat er staat in het plaatje dat je post:
We kunnen dus niet concluderen op basis van de voldoende voorwaarden dat de functie convex of concaaf is.
Er wordt dus niet gezegd dat het het een of het ander is, er wordt gezegd dat het beide niet aantoonbaar is. En die bewering klopt.
Ervaring en inzicht. Je weet bijvoorbeeld dat f(x)=x^3 een zadelpunt heeft op x=0, dus een makkelijk voorbeeld zou f(x,y) = x^3 + y^3 zijn.quote:
Hoe kun je zoiets weten?
[ afbeelding ]
Ik weet dat de voorwaarde voor een zadelpunt het volgende is:
[ afbeelding ]
Hoe kun je het zadelpunt berekenen van een functie met 1 variabele? Daarnaast... Dus x² heeft een minimum, dus een convexe functie zou x² of x² + y² kunnen zijn?quote:
[..]
Ervaring en inzicht. Je weet bijvoorbeeld dat f(x)=x^3 een zadelpunt heeft op x=0, dus een makkelijk voorbeeld zou f(x,y) = x^3 + y^3 zijn.
Heb je enig idee wat een zadelpunt is? En, ik heb het over de derdemacht van x...quote:
[..]
Hoe kun je het zadelpunt berekenen van een functie met 1 variabele? Daarnaast... Dus x² heeft een minimum, dus een convexe functie zou x² of x² + y² kunnen zijn?
Hoe los ik dit op?
Beetje verwarrend door de noemers... Ik had zelf eerst de noemers gelijkgemaakt, maar ja dan kan ik gaan lopen wegstrepen en kom ik weer op hetzelfde uit..
Beetje verwarrend door de noemers... Ik had zelf eerst de noemers gelijkgemaakt, maar ja dan kan ik gaan lopen wegstrepen en kom ik weer op hetzelfde uit..
2/(x+1) naar de rechterkant halen en dan kruislings vermenigvuldigen.quote:
Hoe los ik dit op?
[ afbeelding ]
Beetje verwarrend door de noemers... Ik had zelf eerst de noemers gelijkgemaakt, maar ja dan kan ik gaan lopen wegstrepen en kom ik weer op hetzelfde uit..
Waarom mag je kruislings vermenigvuldigen? Ik hoor dit voor het eerst.quote:
[..]
2/(x+1) naar de rechterkant halen en dan kruislings vermenigvuldigen.
Toch zit daar wel de oplossing.quote:
Hoe los ik dit op?
[ afbeelding ]
Beetje verwarrend door de noemers... Ik had zelf eerst de noemers gelijkgemaakt, maar ja dan kan ik gaan lopen wegstrepen en kom ik weer op hetzelfde uit..
Als je er één breuk van maakt staat er
Die vergelijking kun je oplossen door de teller gelijk aan nul te stellen, en dat is niet zo moeilijk.
Opinion is the medium between knowledge and ignorance (Plato)
Waar heb jij gezeten tijdens de onderbouwquote:
[..]
Waarom mag je kruislings vermenigvuldigen? Ik hoor dit voor het eerst.
Kruislings vermenigvuldigen is iets dat je kan toepassen als je twee breuken aan elkaar gelijkstelt.quote:
[..]
Waarom mag je kruislings vermenigvuldigen? Ik hoor dit voor het eerst.
Bijvoorbeeld
a/b = c/d, dan ad = bc.
Afleiding:
a/b = c/d
vermenigvuldig links en rechts met b
a = bc/d
vermenigvuldig links en rechts met d
ad = bc.
Opinion is the medium between knowledge and ignorance (Plato)
Natuurlijk onder de voorwaarde datquote:
[..]
Kruislings vermenigvuldigen is iets dat je kan toepassen als je twee breuken aan elkaar gelijkstelt.
Bijvoorbeeld
a/b = c/d, dan ad = bc.
Afleiding:
a/b = c/d
vermenigvuldig links en rechts met b
a = bc/d
vermenigvuldig links en rechts met d
ad = bc.
Mag je hier wel gewoon vermenigvuldigen met (x+1)(x+3) (ik heb geleerd van wel)? Feitelijk verander je dan alleen iets aan de linkerkant, en dat brengt me in verwarring.quote:
[..]
Toch zit daar wel de oplossing.
Als je er één breuk van maakt staat er
Die vergelijking kun je oplossen door de teller gelijk aan nul te stellen, en dat is niet zo moeilijk.
Wat krijg je aan de rechterkant als je met (x+1)(x+3) vermenigvuldigt?quote:
[..]
Mag je hier wel gewoon vermenigvuldigen met (x+1)(x+3) (ik heb geleerd van wel)? Feitelijk verander je dan alleen iets aan de linkerkant, en dat brengt me in verwarring.
Nog steeds 0. 0 maal iets is nul.quote:
[..]
Wat krijg je aan de rechterkant als je met (x+1)(x+3) vermenigvuldigt?
Ja ik weet wat een zadelpunt is. Dat heb je meestal bij 3d grafieken.quote:
[..]
Heb je enig idee wat een zadelpunt is? En, ik heb het over de derdemacht van x...
Met andere woorden, je hebt geen flauw idee wat een zadelpunt geometrisch is.quote:
[..]
Ja ik weet wat een zadelpunt is. Dat heb je meestal bij 3d grafieken.
quote:
Ik snap dus die x² > 0 niet... want hoe weet je dat dan? :
Noem mij eens een getal x waarvoor x2 < 0 ?
Opinion is the medium between knowledge and ignorance (Plato)
Precies. Dus als je aan beide kanten met (x+1)(x+3) vermenigvuldigt, krijg je:quote:
x(x+1) -2(x+3) = 0.
Je hebt dan aan beide kanten dezelfde bewerking toegepast. Dit mag dus gewoon. Je moet alleen oppassen als je x=-3 of x=-1 als oplossing krijgt. Deze oplossing zijn namelijk niet toegestaan, omdat dan de noemer 0 wordt.
Een andere manier om hier naar te kijken is door te stellen dat als geldt:
a/b = 0
Dan moet gelden: a=0. Voor a ongelijk aan 0 is er namelijk geen enkele waarde b waarvoor a/b=0
Yep, dat snap ik.quote:
[..]
Precies. Dus als je aan beide kanten met (x+1)(x+3) vermenigvuldigt, krijg je:
x(x+1) -2(x+3) = 0.
Je hebt dan aan beide kanten dezelfde bewerking toegepast. Dit mag dus gewoon. Je moet alleen oppassen als je x=-3 of x=-1 als oplossing krijgt. Deze oplossing zijn namelijk niet toegestaan, omdat dan de noemer 0 wordt.
Een andere manier om hier naar te kijken is door te stellen dat als geldt:
a/b = 0
Dan moet gelden: a=0. Voor a ongelijk aan 0 is er namelijk geen enkele waarde b waarvoor a/b=0
Eigenlijk zijn dus alle bewerkingen toegestaan, zolang je dat maar op beide kanten doet (en niet deelt door nul)?
Ohja...quote:
[..]
Noem mij eens een getal x waarvoor x2 < 0 ?
Inderdaadquote:
[..]
Yep, dat snap ik.
Er zijn wel wat meer uitzonderingen. Het is ook niet zomaar toegestaan om links en rechts te kwadrateren (iets met mintekens) of links en rechts de wortel te trekken (kan ook niet als een van beide kanten wel eens negatief zou kunnen worden).quote:
[..]
Yep, dat snap ik.
Volgens mij is het zo dat het mag zo lang de bewerking die je wil uitvoeren een bijectie R --> R is, maar dat doe ik uit mijn hoofd. Er zijn vast wel mensen hier die dat beter weten.
Opinion is the medium between knowledge and ignorance (Plato)
Ik dacht toch echt dat de teller geen 'infinite'' zou geven, maar niet gedefinieerd, met name omdat er een - teken staat binnen de ln plus dat de limiet nadert naar 0 en ln(0) kan niet.
Stel je hebt de functie gedefinieerd door f(x) = x^3. Dan heb je f'(x)=0 => x=0 met als functiewaarde f(0)=0. Met andere woorden, x=0 is een stationair punt. Zijquote:
[..]
Ja ik weet wat een zadelpunt is. Dat heb je meestal bij 3d grafieken.
Kan je deze logica ook toepassen op f(x,y) = x^3 + y^3?
Wat bedoelen ze meestal met de ε? Een willekeurige letter voor een variabele? Of moet ik er wat achter zoeken?quote:
[..]
Stel je hebt de functie gedefinieerd door f(x) = x^3. Dan heb je f'(x)=0 => x=0 met als functiewaarde f(0)=0. Met andere woorden, x=0 is een stationair punt. Zijgegeven. Dan heb je
en
. Omdat
Kan je deze logica ook toepassen op f(x,y) = x^3 + y^3?
Laat maar, het is een letter voor een variabele met een willekeurig kleine waarde.
[ Bericht 2% gewijzigd door netchip op 21-10-2014 22:33:53 ]
Meestal een afstand. Lastig om uit te leggen, dit kan Riparius waarschijnlijk perfect uitleggen.quote:
[..]
Wat bedoelen ze meestal met de ε? Een willekeurige letter voor een variabele? Of moet ik er wat achter zoeken?
Niet willekeurig klein. Enkel willekeurig. Het ene impliceert het andere, maar de andere niet de ene om het maar super vaag te zeggen.quote:
[..]
Wat bedoelen ze meestal met de ε? Een willekeurige letter voor een variabele? Of moet ik er wat achter zoeken?
Laat maar, het is een letter voor een variabele met een willekeurig kleine waarde.
Wikipedia zei dit er over (http://nl.wikipedia.org/wiki/Epsilon#Wiskunde): "In de wiskunde wordt de epsilon gebruikt om willekeurig kleine getallen aan te geven, bijvoorbeeld bij limieten." Ik geloof je best hoor, alleen ik ging hier op af.quote:
[..]
Niet willekeurig klein. Enkel willekeurig. Het ene impliceert het andere, maar de andere niet de ene om het maar super vaag te zeggen.
Dan heeft Wikipedia (zoals wel vaker) het fout.quote:
[..]
Wikipedia zei dit er over (http://nl.wikipedia.org/wiki/Epsilon#Wiskunde): "In de wiskunde wordt de epsilon gebruikt om willekeurig kleine getallen aan te geven, bijvoorbeeld bij limieten." Ik geloof je best hoor, alleen ik ging hier op af.
Het wordt (bijna) altijd in de context gebruikt van: Zij ε>0 gegeven. Zie jij iets dat willekeurig klein zou moeten aanduiden?
Nope...quote:
[..]
Dan heeft Wikipedia (zoals wel vaker) het fout.
Het wordt (bijna) altijd in de context gebruikt van: Zij ε>0 gegeven. Zie jij iets dat willekeurig klein zou moeten aanduiden?
Bij een limiet is het onbelangrijk wat er gebeurt op het punt zelf. Je moet alleen kijken naar waar het heel dicht nadert.quote:
[ afbeelding ]
[ afbeelding ]
Ik dacht toch echt dat de teller geen 'infinite'' zou geven, maar niet gedefinieerd, met name omdat er een - teken staat binnen de ln plus dat de limiet nadert naar 0 en ln(0) kan niet.
[ afbeelding ]
Wat ik zelf bedenk bij zoiets: x gaat naar 0 vanaf onder. Dus uiteindelijk krijg je iets als -.0000000001 voor x. Wanneer je dat invult voor x krijg je in de teller dus -ln(0.00000001). Wat dus wel gedefinieerd is! Als je dan de grafiek van ln(x) bedenkt moet je je realiseren dat ln(0,000001) dus nadert naar -oneindig, omdat er nu nog een minteken voor de ln staat wordt dat dus een + oneindig. De noemer wordt 2. Dus limiet = oneindig.
Een snelle theorie vraag, conjugatie van een pure quaternion beeldt deze opnieuw af op een pure quaternion, en dit moet een rotatie in R3 simuleren. Maar wat is de groepsoperatie, en wat is dan de bijbehorende inverse? Standaard vermenigvuldiging?
Cuius rei demonstrationem mirabilem sane detexi hanc marginis exiguitas non caparet
Een vraagje:
Bepaal de volgende limiet: limx->0 (ln(1+x))/(ln(1-x))
zonder gebruik te maken van l'hopital.
Bepaal de volgende limiet: limx->0 (ln(1+x))/(ln(1-x))
zonder gebruik te maken van l'hopital.
hallo
Met behulp van taylorseries voor ln(1+x) en ln(1-x) is een manier.quote:
Een vraagje:
Bepaal de volgende limiet: limx->0 (ln(1+x))/(ln(1-x))
zonder gebruik te maken van l'hopital.
Dat deed Wolfram ook. Maar het kwam op een tentamen basiswiskunde (econometrie, 1e jaars vak). Taylor series zijn bij ons nog niet behandeld.quote:Met behulp van taylorseries voor ln(1+x) en ln(1-x) is een manier.
Je moet de volgende standaardlimieten gebruiken:
1) limx->0 ln(1+x) / x = 1
2) limx->1 ln(x) / (x-1) = 1
hallo
Je kunt je limiet opvatten als het quotiënt van de limietenquote:
[..]
Dat deed Wolfram ook. Maar het kwam op een tentamen basiswiskunde (econometrie, 1e jaars vak). Taylor series zijn bij ons nog niet behandeld.
Je moet de volgende standaardlimieten gebruiken:
1) limx->0 ln(1+x) / x = 1
2) limx->1 ln(x) / (x-1) = 1
en
waarbij de eerste volgt uit de definitie van de afgeleide en de tweede volgt uit de eerste door x te vervangen door −x. Zo vind je direct dat
Zéér basic dit maar ik kom er niet uit?
Wortel N = 5-4N
kwadrateren dus want wortel.
Dus krijg je; N =(5-4N)kwadraat
Dan vereenvoudig je, dus
N = 25-16N, toch?
Het antwoordenboekje zegt dat er bij N =(5-4N)kwadraat N= 25-40N + 16N kwadraat moet uitkomen, hoe dan?
Wortel N = 5-4N
kwadrateren dus want wortel.
Dus krijg je; N =(5-4N)kwadraat
Dan vereenvoudig je, dus
N = 25-16N, toch?
Het antwoordenboekje zegt dat er bij N =(5-4N)kwadraat N= 25-40N + 16N kwadraat moet uitkomen, hoe dan?
1 op de 6 mensen heeft 5 anderen om zich heen
-Harry Jekkers
-Harry Jekkers
Wikipedia heeft het niet echt fout, alleen is het citaat dat Netchip aanhaalt afkomstig uit het artikel over de Griekse letter ε en niet over een wiskundig onderwerp en om deze reden informeel geformuleerd. We zeggen datquote:
[..]
Dan heeft Wikipedia (zoals wel vaker) het fout.
Het wordt (bijna) altijd in de context gebruikt van: Zij ε>0 gegeven. Zie jij iets dat willekeurig klein zou moeten aanduiden?
als er voor elke ε > 0 een δ > 0 bestaat zodanig dat
voor elke x zodanig dat
Welnu, als er voor een zekere ε0 > 0 een δ0 bestaat die aan het in de definitie gestelde voldoet, dan zal voor elke willekeurige ε > ε0 dezelfde δ0 eveneens aan het in de definitie gestelde voldoen, aangezien uit | f(x) − L | < ε0 en tevens ε0 < ε volgt dat | f(x) − L | < ε. We zien dus dat 'grote' waarden van ε helemaal niet relevant of interessant zijn voor de definitie van de limiet, maar dat het er de facto om gaat dat er voor elke willekeurige kleine positieve waarde van ε een δ > 0 bestaat die aan het gestelde voldoet. De definitie van de limiet komt er dus op neer dat we de afstand tussen f(x) en L willekeurig klein kunnen maken als we de afstand tussen x en a maar voldoende klein maken. Het gebruik van de letters ε en δ in wat de ε,δ-definitie van de limiet is gaan heten gaat terug op Cauchy, die deze letters kennelijk koos omdat de overeenkomstige Latijnse letters e en d de eerste letters zijn van de Franse woorden erreur en différence. De definitie houdt immers in dat we de afwijking (: erreur) van f(x) met L kleiner kunnen maken dan ε door het verschil (: différence) van x met a kleiner te maken dan δ. De huidige precieze vorm van de definitie van een limiet is overigens pas later gegeven door Weierstraß, die daarvoor ook de absoluutstrepen introduceerde om de definitie compact op te kunnen schrijven.
N = (5-4N)2quote:Op woensdag 22 oktober 2014 16:11 schreef Nelvalhil het volgende:
Zéér basic dit maar ik kom er niet uit?
Wortel N = 5-4N
kwadrateren dus want wortel.
Dus krijg je; N =(5-4N)kwadraat
Dan vereenvoudig je, dus
N = 25-16N, toch?
Het antwoordenboekje zegt dat er bij N =(5-4N)kwadraat N= 25-40N + 16N kwadraat moet uitkomen, hoe dan?
N = (5-4N)(5-4N)
N = 25 - 20N - 20N + 16N2
16N2 - 41N + 25 = 0
(N-1)(16N-25) = 0,
Dus N=1. Ook N = 25/16 zou een oplossing kunnen zijn, ware het niet dat die niet in het domein van de oorspronkelijke wortel zit.
Opinion is the medium between knowledge and ignorance (Plato)
Godverdommequote:
N = (5-4N)2
N = (5-4N)(5-4N)
N = 25 - 20N - 20N + 16N2
16N2 - 41N + 25 = 0
(N-1)(16N-25) = 0,
Dus N=1 of N = 25/16.
tuurlijk.. Dank je wel 
1 op de 6 mensen heeft 5 anderen om zich heen
-Harry Jekkers
-Harry Jekkers
NEE. Shame on you. Leer je merkwaardige producten. Het kwadraat van een verschil van twee grootheden is niet gelijk aan het verschil van de kwadraten van die grootheden.quote:
Zéér basic dit maar ik kom er niet uit?
Wortel N = 5-4N
kwadrateren dus want wortel.
Dus krijg je; N =(5-4N)kwadraat
Dan vereenvoudig je, dus
N = 25-16N, toch?
Volgens mij maak je nog een foutje, want er is maar één oplossing.quote:
N = (5-4N)2
N = (5-4N)(5-4N)
N = 25 - 20N - 20N + 16N2
16N2 - 41N + 25 = 0
(N-1)(16N-25) = 0,
Dus N=1 of N = 25/16.
Goed punt, de wortel van (5-100/16) bestaat natuurlijk niet.quote:
[..]
Volgens mij maak je nog een foutje, want er is maar één oplossing.
Opinion is the medium between knowledge and ignorance (Plato)
Nee. Het klopt, volgens mijquote:
[..]
Volgens mij maak je nog een foutje, want er is maar één oplossing.
1 op de 6 mensen heeft 5 anderen om zich heen
-Harry Jekkers
-Harry Jekkers
Hoezo zou het niet kloppen? N = 1 v N= 1 9/16
1 op de 6 mensen heeft 5 anderen om zich heen
-Harry Jekkers
-Harry Jekkers
Is het daarom niet handiger gelijk na het kwadrateren het domein aan te geven voor die vergelijking?quote:
[..]
Goed punt, de wortel van (5-100/16) bestaat natuurlijk niet.
Op de middelbare school moesten we de oplossing weer terug invullen in de vergelijking om te controleren of hij klopt.
Maar als je gewoon gelijk het domein aangeeft hoef je dat helemaal niet te doen.
Na het kwadraten krijg je twee vergelijkingen de ene voor het domein x =< 5/4 en de andere x > 5/4.quote:
Hoezo zou het niet kloppen? N = 1 v N= 1 9/16
De oplossing van de vergelijking die zij opgelost heeft zit niet in dat domein (19/16 > 5/4). Daarnaast heeft de andere vergelijking geen enkele oplossing in het domein.
Er is dus maar één oplossing.
Nee, maar daar gaat het hier niet om. De beide oplossingen van de vierkantsvergelijking in N zijn positief, dus √N bestaat voor elk van beide waarden van N die je vindt. Alleen is een vierkantswortel niet negatief waardoor de oplossing N = 25/16 komt te vervallen, maar dat is wat anders.quote:
[..]
Goed punt, de wortel van (5-100/16) bestaat natuurlijk niet.
Ik heb mijzelf inderdaad wat slordig verwoord. Excuus.
Want
Want
quote:Is het daarom niet handiger gelijk na het kwadrateren het domein aan te geven voor die vergelijking?
Opinion is the medium between knowledge and ignorance (Plato)
quote:
[..]
Nee, maar daar gaat het hier niet om. De beide oplossingen van de vierkantsvergelijking in N zijn positief, dus √N bestaat voor elk van beide waarden van N die je vindt. Alleen is een vierkantswortel niet negatief waardoor de oplossing N = 25/16 komt te vervallen, maar dat is wat anders.
Dit ja
1 op de 6 mensen heeft 5 anderen om zich heen
-Harry Jekkers
-Harry Jekkers
Differentiëren lukt me nu wel aardig, al heb ik met dit (post van Riparius over de notatie van Leibniz) nog wel moeite, maar ook daar begint het kwartje te vallen.
Ik ben nu dus aan het kijken naar het integreren van een functie. Als je hebt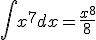
, dan klinkt dat totaal logisch. De afgeleide van x8/8 zou gewoon x7 zijn. Maar nu ben ik dus aan het kijken naar integreren door substitutie, en dat ziet er voor mij een beetje als goochelen uit. Wanneer kan ik deze methode toepassen, en hoe werkt deze? Ik weet dat het het tegenovergestelde van de kettingregel is. Stel 
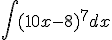, dan doe je de substitutie u = 10x-8. Oké, maar wat gebeurt er met de differentiaal dx? Zou iemand daar uitleg over kunnen geven?
Ik ben nu dus aan het kijken naar het integreren van een functie. Als je hebt
Als je u = 10x-8 hebt, dan heb je du/dx = 10 en "dus" du = 10dx. Dan heb je dus de integraal
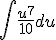
Ik ben vergeten hoe je dit rigoureus opschrijft, maar dit is genoeg om te weten hoe je het kan toepassen.
Ik ben vergeten hoe je dit rigoureus opschrijft, maar dit is genoeg om te weten hoe je het kan toepassen.
En dat wordt du, omdat je gaat integreren naar u? En... Je krijgt daar een deling door 10 omdat dx = du/10 = du * 1/10?quote:
Als je u = 10x-8 hebt, dan heb je du/dx = 10 en "dus" du = 10dx. Dan heb je dus de integraal
Ik ben vergeten hoe je dit rigoureus opschrijft, maar dit is genoeg om te weten hoe je het kan toepassen.
Als je dan
Nee, er volgt direct datquote:
[..]
En dat wordt du, omdat je gaat integreren naar u? En... Je krijgt daar een deling door 10 omdat dx = du/10 = du * 1/10?
Als je danhebt, en je wilt dit weer substitueren met de waardes van u, krijg je dan
? Waarom kan hier de du weer vervangen worden door dx zonder te delen door 10 (want dx = du/10)?
Nu kun je weer substitueren.
Je hebt:quote:
[..]
En dat wordt du, omdat je gaat integreren naar u? En... Je krijgt daar een deling door 10 omdat dx = du/10 = du * 1/10?
Als je dan
Waarom mag je de differentiaal du hier vervangen door de integratieconstante?quote:
[..]
Nee, er volgt direct dat
Nu kun je weer substitueren.
Dat doe ik niet, ik evalueer hier gewoon de integraal. Overigens:quote:
[..]
Waarom mag je de differentiaal du hier vervangen door de integratieconstante?
Je vergeet hier de integratieconstante.
Ik raad je aan je eerst even wat beter te verdiepen in de zogenaamde 'u-substitution', want volgensmij is het nu nog abacadabra voor je. Hier alvast een link.
Even wat anders,
"De top van de grafiek van f(x) = x2+px+3 ligt op de lijn y = x+1."
Wat ik deed is xtop = -b/2a = -p/2, en dan zeggen f(-p/2) = x+1. Dit ging natuurlijk fout omdat ik dan twee variabelen heb, en in het uitwerkingenboek zeggen ze dat je de ytop moet invullen in y = x+1. Dit lijkt me sterk, want waarom vul je de y-coördinaat van een top van een parabool in in een formule voor een y-coödinaat?!
"De top van de grafiek van f(x) = x2+px+3 ligt op de lijn y = x+1."
Wat ik deed is xtop = -b/2a = -p/2, en dan zeggen f(-p/2) = x+1. Dit ging natuurlijk fout omdat ik dan twee variabelen heb, en in het uitwerkingenboek zeggen ze dat je de ytop moet invullen in y = x+1. Dit lijkt me sterk, want waarom vul je de y-coördinaat van een top van een parabool in in een formule voor een y-coödinaat?!
Je geeft al aan dat de substitutieregel bij het integreren (c.q. primitiveren) de tegenhanger is van de kettingregel bij het differentiëren, en daarmee zou je antwoord kunnen geven op je eigen vraag. Als F een primitieve is van een reële functie f van een reële variabele x, dan hebben wequote:
Differentiëren lukt me nu wel aardig, al heb ik met dit (post van Riparius over de notatie van Leibniz) nog wel moeite, maar ook daar begint het kwartje te vallen.
Ik ben nu aan het kijken naar het integreren van een functie. Als je hebt
waarbij C een willekeurige (reële) constante is. Een onbepaalde integraal van een functie is zo niets anders dan een notatie voor de verzameling van alle primitieven van de gegeven functie aangezien elk tweetal primitieven van een functie slechts een constante van elkaar verschilt. Deze notatie moet niet worden verward met de hoofdstelling van de integraalrekening die betrekking heeft op een bepaalde integraal en die zegt dat als f: [a,b] → R een continue functie is en F een primitieve van f, dat dan geldt
Kijk hier voor een eenvoudige uitleg van de hoofdstelling van de integraalrekening en de origine van deze notaties.
Substitueren we nu x = φ(u) waarbij φ een differentieerbare functie is, dan is de afgeleide van F(φ(u)) naar u volgens de kettingregel gelijk aan F'(φ(u))φ'(u) = f(φ(u))φ'(u), zodat omgekeerd F(φ(u)) een primitieve is van f(φ(u))φ'(u) en we dus hebben
en daarmee
Is φ: [α,β] → [a,b] een differentieerbare functie met a = φ(α), b = φ(β) dan is F(b) − F(a) = F(φ(β)) − F(φ(α)) zodat we volgens de hoofdstelling van de integraalrekening ook hebben
De notatie en de symboliek van Leibniz maken het, evenals bij de kettingregel, weer gemakkelijk om de substitutieregel te onthouden en te gebruiken. Substitueren we
dan is
en daarmee (symbolisch)
zodat je gemakkelijk onthoudt dat je dx door φ'(u)du moet vervangen als je x door φ(u) vervangt, zie ook hier.
In de praktijk gebruik je bovenstaande substitutieregel ook vaak van rechts naar links, en dan heb je als we de rollen van x en u verwisselen
Hier substitueren we
zodat
en daarmee
zodat we weer gemakkelijk zien dat we φ'(x)dx moeten vervangen door du als we φ(x) vervangen door u. Is φ: [α,β] → [a,b] een differentieerbare functie met φ(α) = a, φ(β) = b, dan is F(φ(β)) − F(φ(α)) = F(b) − F(a) en hebben we dus volgens de hoofdstelling van de integraalrekening ook
Tot slot, aangezien we ook kunnen schrijven
en daarmee
kunnen we ook schrijven
hetgeen neerkomt op een impliciete substitutie. Immers, substitueren we u = φ(x) in
dan staat er niets anders dan
Hebben we nu bijvoorbeeld
dan kunnen we bedenken dat
en daarmee
oftewel
zodat
[ Bericht 0% gewijzigd door Riparius op 27-10-2014 12:42:18 ]
Je begrijpt de opgave duidelijk niet. De top van de grafiek van f(x) = x2 + px + 3 moet op de lijn met vergelijking y = x + 1 liggen, dus als de top van de grafiek van f de coördinaten (xtop; ytop) heeft, dan moeten deze coördinaten voldoen aan de betrekkingquote:
Even wat anders,
"De top van de grafiek van f(x) = x2+px+3 ligt op de lijn y = x+1."
Wat ik deed is xtop = -b/2a = -p/2, en dan zeggen f(-p/2) = x+1. Dit ging natuurlijk fout omdat ik dan twee variabelen heb, en in het uitwerkingenboek zeggen ze dat je de ytop moet invullen in y = x+1. Dit lijkt me sterk, want waarom vul je de y-coördinaat van een top van een parabool in in een formule voor een y-coördinaat?!
ytop = xtop + 1
Je bent er dus niet door alleen xtop uit te drukken in p, maar je moet ook ytop uitdrukken in p en dan beide uitdrukkingen invullen in deze betrekking, zodat je een vergelijking in p krijgt die je vervolgens op kunt lossen.
Ik ging er van uit dat de waarde van ytop gelijk moest zijn aan x+1, omdat de lijn x+1 en de top elkaar moesten snijden. Ik snap nog steeds niet waarom ik de x- en y-coördinaten moet invullen, maar ik zal er nog even over nadenken.quote:
[..]
Je begrijpt de opgave duidelijk niet. De top van de grafiek van f(x) = x2 + px + 3 moet op de lijn met vergelijking y = x + 1 liggen, dus als de top van de grafiek van f de coördinaten (xtop; ytop) heeft, dan moeten deze coördinaten voldoen aan de betrekking
ytop = xtop + 1
Je bent er dus niet door alleen xtop uit te drukken in p, maar je moet ook ytop uitdrukken in p en dan beide uitdrukkingen invullen in deze betrekking, zodat je een vergelijking in p krijgt die je vervolgens op kunt lossen.
Dit is niet nauwkeurig genoeg, en dat is precies je probleem. Bedenk eens wat je hier bedoelt met x. En er is niet zoiets als een lijn x + 1. Je hebt een lijn met als vergelijking y = x + 1.quote:
[..]
Ik ging er van uit dat de waarde van ytop gelijk moest zijn aan x+1, omdat de lijn x+1 en de top elkaar moesten snijden.
De top van de parabool die de grafiek is van je kwadratische functie heeft de coördinaten (xtop; ytop) en gevraagd wordt nu p zo te bepalen dat deze top op de rechte met vergelijking y = x + 1 ligt, zodat geldtquote:Ik snap nog steeds niet waarom ik de x- en y-coördinaten moet invullen, maar ik zal er nog even over nadenken.
ytop = xtop + 1
Nu had je al bedacht dat
xtop = −p/2
zodat je dus hebt
(1) ytop = −p/2 + 1
Maar je hebt ook
(2) ytop = f(xtop)
en uit (1) en (2) volgt
(3) f(xtop) = −p/2 + 1
oftewel
(4) f(−p/2) = −p/2 + 1
Wat denk je hiervan?
Ah, je hebt twee vergelijkingen voor lijnen, f(x) en y = x + 1. In beide moet je de xtop invullen, en dan gelijk stellen aan elkaar, omdat de waarde van f(xtop) gelijk moet zijn aan de waarde van xtop + 1. Dank je!quote:
[..]
Dit is niet nauwkeurig genoeg, en dat is precies je probleem. Bedenk eens wat je hier bedoelt met x. En er is niet zoiets als een lijn x + 1. Je hebt een lijn met als vergelijking y = x + 1.
[..]
De top van de parabool die de grafiek is van je kwadratische functie heeft de coördinaten (xtop; ytop) en gevraagd wordt nu p zo te bepalen dat deze top op de rechte met vergelijking y = x + 1 ligt, zodat geldt
ytop = xtop + 1
Nu had je al bedacht dat
xtop = −p/2
zodat je dus hebt
(1) ytop = −p/2 + 1
Maar je hebt ook
(2) ytop = f(xtop)
en uit (1) en (2) volgt
(3) f(xtop) = −p/2 + 1
oftewel
(4) f(−p/2) = −p/2 + 1
Wat denk je hiervan?
Wellicht is mijn vraag iets te simpel voor dit topic, maar goed
Ik heb moeite met het bewijzen van verzamelingen en het venndiagram die hierbij hoort.
Ik loop bijvoorbeeld vast als ik het venndiagram moet maken voor A ∩ ( B ∪ A ). Wat moet worden gearceerd, waar kruist A en B met elkaar
En het bewijzen van A ∩ ( B ∪ A ) = A
Voor mijzelf is bovenstaande logisch, het bewijzen hiervan blijkt echter lastiger dan gedacht
Poging tot bewijzen:
x ∈ A
x ∈ B ∪ A
Als x ∈ B ∪ A en x ∈ A dan is A ⊂ (B ∪ A)
Hier loop ik vast. Hoe werk ik dit verder uit?
Ik heb moeite met het bewijzen van verzamelingen en het venndiagram die hierbij hoort.
Ik loop bijvoorbeeld vast als ik het venndiagram moet maken voor A ∩ ( B ∪ A ). Wat moet worden gearceerd, waar kruist A en B met elkaar
En het bewijzen van A ∩ ( B ∪ A ) = A
Voor mijzelf is bovenstaande logisch, het bewijzen hiervan blijkt echter lastiger dan gedacht
Poging tot bewijzen:
x ∈ A
x ∈ B ∪ A
Als x ∈ B ∪ A en x ∈ A dan is A ⊂ (B ∪ A)
Hier loop ik vast. Hoe werk ik dit verder uit?
Teken twee cirkels die elkaar kruisen, de ene is A en de andere is B.quote:
Wellicht is mijn vraag iets te simpel voor dit topic, maar goed
Ik heb moeite met het bewijzen van verzamelingen en het venndiagram die hierbij hoort.
Ik loop bijvoorbeeld vast als ik het venndiagram moet maken voor A ∩ ( B ∪ A ). Wat moet worden gearceerd, waar kruist A en B met elkaar
Wat is dan B ∪ A ?
quote:
[..]
Teken twee cirkels die elkaar kruisen, de ene is A en de andere is B.
Wat is dan B ∪ A ?
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.kloep kloep
quote:
[..]
Teken twee cirkels die elkaar kruisen, de ene is A en de andere is B.
Wat is dan B ∪ A ?
Aangezien A wordt verenigd met B, is het resultaat een venndiagram die alle elementen bevat van zowel A als B. Vandaar dezelfde kleur
Oké, noemen we die set C, wat is dan A ∩ C?quote:
[..]
[ afbeelding ]
Aangezien A wordt verenigd met B, is het resultaat een venndiagram die alle elementen bevat van zowel A als B. Vandaar dezelfde kleur
quote:
[..]
Oké, noemen we die set C, wat is dan A ∩ C?
quote:
Het kwartje begint enigszins te vallen
(denk ik)Wat ik hier overigens niet helemaal begrijp: waarom wordt een deel van B ook meegenomen in A ∩ C
[ Bericht 3% gewijzigd door Stickers op 23-10-2014 12:43:00 ]
wow nvm foutjequote:
[..]
[ afbeelding ]
Het kwartje begint enigszins te vallen
Wat ik hier overigens niet helemaal begrijp: waarom wordt een deel van B ook meegenomen in A ∩ C
C = A v B, dus A ^ C = A ^ ( A v B)
[ Bericht 2% gewijzigd door #ANONIEM op 23-10-2014 12:58:59 ]
Gewoon definities van doorsnee en vereniging uitschrijven.quote:
Wellicht is mijn vraag iets te simpel voor dit topic, maar goed
Ik heb moeite met het bewijzen van verzamelingen en het venndiagram die hierbij hoort.
Ik loop bijvoorbeeld vast als ik het venndiagram moet maken voor A ∩ ( B ∪ A ). Wat moet worden gearceerd, waar kruist A en B met elkaar
En het bewijzen van A ∩ ( B ∪ A ) = A
Voor mijzelf is bovenstaande logisch, het bewijzen hiervan blijkt echter lastiger dan gedacht
Poging tot bewijzen:
x ∈ A
x ∈ B ∪ A
Als x ∈ B ∪ A en x ∈ A dan is A ⊂ (B ∪ A)
Hier loop ik vast. Hoe werk ik dit verder uit?
Een willekeurig element x uit A^(BvA) zit in A en in (BvA).
(BvA) kun je dan weer schrijven als x zit in B of x zit in A.
Nu is het jou beurt.
Volgens mij moet je de productregel gebruiken.quote:
Weet iemand wat de afgeleide is van
f(x)= xyx-1
?
Echt doe nou even moeite.quote:
Weet iemand wat de afgeleide is van
f(x)= xyx-1
?
Dit probleem zou je nu wel moeten kunnen oplossen.
Welke regels ken je allemaal? Welke kan je toepassen, waar loop je vast?
Ik kan je wel een antwoord geven, maar dan kan je net zo goed Wolfram Alpha/Mathematica gebruiken.
Ik kom er niet uit..quote:
[..]
Echt doe nou even moeite.
Dit probleem zou je nu wel moeten kunnen oplossen.
Welke regels ken je allemaal? Welke kan je toepassen, waar loop je vast?
Ik kan je wel een antwoord geven, maar dan kan je net zo goed Wolfram Alpha/Mathematica gebruiken.
Een uitwerking zou super zijn.
Oriëntatie behoudende rotaties van R3 worden gegeven door SO(3). Je hebt zoals je weet een conjugatie norm op de quaternionen. En daarmee kun je laten zien dat de quaternionen met norm 1 onder de standaard vermenigvuldiging van de quaternionen een groep vormen en isomorf zijn aan SU(2) als groep. Iets soort gelijk kun je ook doen met de pure quaternionen en SO(3). Hint, laat zien dat de generende elementen van beide groepen hetzelfde gedragen onder hun eigen operatie.quote:Op woensdag 22 oktober 2014 00:03 schreef Diacetylmorfine het volgende:
Een snelle theorie vraag, conjugatie van een pure quaternion beeldt deze opnieuw af op een pure quaternion, en dit moet een rotatie in R3 simuleren. Maar wat is de groepsoperatie, en wat is dan de bijbehorende inverse? Standaard vermenigvuldiging?
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Je weet dat je (voor a > 0) hebtquote:
[..]
Ik kom er niet uit..
Een uitwerking zou super zijn.
en zo hebben we dus (voor y > 0) ook
Nu is verder
en daarmee ook
Nu heb je verder volgens de productregel
De rest kun je nu zelf wel bedenken.
Daar kom ik dus niet uit. Het bewijzen van dergelijke stellingen. Hoe bewijs ik A ∩ ( B ∪ A ) = A ?quote:
[..]
Gewoon definities van doorsnee en vereniging uitschrijven.
Een willekeurig element x uit A^(BvA) zit in A en in (BvA).
(BvA) kun je dan weer schrijven als x zit in B of x zit in A.
Nu is het jou beurt.
Bijv.: neem een willekeurige x uit A^(BvA) <=> x∈ A en x∈ (BvA) <=> x∈ A en x ∈ (B of A) <=> x ∈ (A en B) of x∈ (A en A) <=> x ∈ A.quote:
[..]
Daar kom ik dus niet uit. Het bewijzen van dergelijke stellingen. Hoe bewijs ik A ∩ ( B ∪ A ) = A ?
Gewoon veel oefenen dan lukt het wel. Daarnaast kun je ook een Venn-diagram tekenen om het voor jezelf helder te hebben.
Je moet bewijzen dat A ∩ (B ∪ A) ⊆ A en dat A ⊆ A ∩ (B ∪ A).quote:
[..]
Daar kom ik dus niet uit. Het bewijzen van dergelijke stellingen. Hoe bewijs ik A ∩ ( B ∪ A ) = A ?
Eerst maar eens bewijzen dat A ⊆ A ∩ (B ∪ A).
Laat x ∈ A. Nu volgt (uit de definitie voor vereniging/union) x ∈ (B ∪ A).
Dan hebben we x ∈ A en x ∈ (B ∪ A), dus (wederom volgens definitie) x ∈ A ∩ (B ∪ A).
Kan jij nu bewijzen dat A ∩ (B ∪ A) ⊆ A?
[ Bericht 1% gewijzigd door zerak op 24-10-2014 00:08:16 ]
quote:
[..]
Bijv.: neem een willekeurige x uit A^(BvA) <=> x∈ A en x∈ (BvA) <=> x∈ A en x ∈ (B of A) <=> x ∈ (A en B) of x∈ (A en A) <=> x ∈ A.
Gewoon veel oefenen dan lukt het wel. Daarnaast kun je ook een Venn-diagram tekenen om het voor jezelf helder te hebben.
Edit, maar verwijderde blijkbaar alles...quote:
[..]
Je moet bewijzen dat A ∩ (B ∪ A) ⊆ A en dat A ⊆ A ∩ (B ∪ A).
Eerst maar eens bewijzen dat A ⊆ A ∩ (B ∪ A).
Laat x ∈ A. Nu volgt (uit de definitie voor vereniging/union) x ∈ (B ∪ A).
Dan hebben we x ∈ A en x ∈ (B ∪ A), dus (wederom volgens definitie) x ∈ A ∩ (B ∪ A).
Kan jij nu bewijzen dat A ∩ (B ∪ A) ⊆ A?
Het bewijzen van A ⊂ A ∩ (B ∪ A) is geen probleem. Het omgekeerde A ∩ (B ∪ A) ⊂ A bewijzen lukt mij juist niet
[ Bericht 100% gewijzigd door Stickers op 23-10-2014 22:28:45 ]
Je moet twee dingen laten zien: de eerste is bevat in de tweede en dat de twee bevat is in de eerste. Dat doe je door een element te pakken bijvoorbeeld in de tweede en dan te laten zien dat het ook in de eerste zit.quote:
[..]
Daar kom ik dus niet uit. Het bewijzen van dergelijke stellingen. Hoe bewijs ik A ∩ ( B ∪ A ) = A ?
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
LAAT DAN ZIEN WAAR JE VAST ZIT!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!quote:
[..]
Ik kom er niet uit..
Een uitwerking zou super zijn.
echt...
Maar nu heeft Riparius je al weer het antwoord gegeven en kijk je niet meer naar de vraag om.
Hoog tijd voor een "geen uitwerkingen"-regel. Ik heb iets te vaak het idee dat ik andermans huiswerk aan het maken ben.quote:
[..]
LAAT DAN ZIEN WAAR JE VAST ZIT!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
echt...
Maar nu heeft Riparius je al weer het antwoord gegeven en kijk je niet meer naar de vraag om.
Een paar berichten terug lezen.quote:
Hoi,
Iemand bekend met wat ik hier moet doen om deze vergelijking op te lossen?:
[ afbeelding ]
Of is dit een déjà vu?
Nee, dinsdag is precies dezelfde vraag langs gekomen.
Maar wat dacht je van vermenigvuldigen met (x+1)(x+3)?
A ∩ (B ∪ A) ⊆ A.quote:
[..]
[..]
Edit, maar verwijderde blijkbaar alles...
Het bewijzen van A ⊂ A ∩ (B ∪ A) is geen probleem. Het omgekeerde A ∩ (B ∪ A) ⊂ A bewijzen lukt mij juist niet
Laat x ∈ A ∩ (B ∪ A).
Nu hebben we (volgens definities) twee gevallen;
(1) x ∈ A en x ∈ B.
(2) x ∈ A (en x ∈ A).
En zo zien we dat in beide gevallen x ∈ A.
Misschien begint er een belletje te rinkelen als je het eens schrijft alsquote:
Hoi,
Iemand bekend met wat ik hier moet doen om deze vergelijking op te lossen?:
[ afbeelding ]
Dus je keert het bewijs simpelweg om?quote:
[..]
A ∩ (B ∪ A) ⊆ A.
Laat x ∈ A ∩ (B ∪ A).
Nu hebben we (volgens definities) twee gevallen;
(1) x ∈ A en x ∈ B.
(2) x ∈ A (en x ∈ A).
En zo zien we dat in beide gevallen x ∈ A.
Volledige uitwerking:
Als x ∈ A dan is ook x ∈ A ∪ B
Uit bovenstaande volgt dat x ∈ A ∩ (B ∪ A)
Hiermee is bewezen dat A ⊂ A ∩ (B ∪ A)
Neem x ∈ A ∩ (B ∪ A) ⊂ A
Hieruit volgt:
x ∈ A ∩ (B ∪ A)
x ∈ A ∪ B
x ∈ A
Hier mee is bewezen dat A ∩ (B ∪ A) ⊂ A
Omdat A ∩ (B ∪ A) ⊂ A en A ⊂ A ∩ (B ∪ A) is A ∩ (B ∪ A) = A
Wiskunde tentamen achter de rug! Het was echt heel makkelijk, met name omdat ik enorm goed voorbereid was t.o.v. de rest. Sowieso een voldoende. Ik verwacht een minstens een 6,5/7.0
Dank jullie allen voor de tijd en moeite om mij te helpen!
Waar ik het meest tevreden over ben, is dat ik de stof onder de knie heb!
Dank jullie allen voor de tijd en moeite om mij te helpen!
Waar ik het meest tevreden over ben, is dat ik de stof onder de knie heb!
Uit je postgeschiedenis blijkt iig alles behalve, maar wie weetquote:
Wiskunde tentamen achter de rug! Het was echt heel makkelijk, met name omdat ik enorm goed voorbereid was t.o.v. de rest. Sowieso een voldoende. Ik verwacht een minstens een 6,5/7.0
Dank jullie allen voor de tijd en moeite om mij te helpen!
Waar ik het meest tevreden over ben, is dat ik de stof onder de knie heb!
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |