SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
Als iemand bereid is om mij met een vraagstuk te helpen met betrekking tot het differentiëren ofwel het bepalen van de afgeleide, graag! Ik ben een beetje radeloos geworden met dit vraagstuk:
''Bereken met behulp van de quotiëntregel de afgeleide van:''
e^x / (1 + e^x )
De quotiëntregel is als volgt: ( f(x) / g(x) ) ' = f'(x) g(x) - f(x) g' (x) / (g(x))²
De noemer is simpel, die moet van (1+e^x) veranderen in: (1+e^x)²
De teller daarentegen is mij een raadsel.
Zelf denk ik dat de teller het volgende moet worden (aan de hand van de quotiëntregel):
e^x * ( 1+e^x) - e^x * ( e^x)
Het uitwerken van dit resulteert tot:
e^x + e^x² - e^x²
Vervolgens wordt de teller dit, na het vereenvoudigen:
e^x
De uiteindelijke afgeleide (samen met de noemer, die ik eerder behandeld heb) wordt:
e^x / (1+e^x)²
Zit ik een beetje correct of heb ik de plank compleet misgeslagen?
''Bereken met behulp van de quotiëntregel de afgeleide van:''
e^x / (1 + e^x )
De quotiëntregel is als volgt: ( f(x) / g(x) ) ' = f'(x) g(x) - f(x) g' (x) / (g(x))²
De noemer is simpel, die moet van (1+e^x) veranderen in: (1+e^x)²
De teller daarentegen is mij een raadsel.
Zelf denk ik dat de teller het volgende moet worden (aan de hand van de quotiëntregel):
e^x * ( 1+e^x) - e^x * ( e^x)
Het uitwerken van dit resulteert tot:
e^x + e^x² - e^x²
Vervolgens wordt de teller dit, na het vereenvoudigen:
e^x
De uiteindelijke afgeleide (samen met de noemer, die ik eerder behandeld heb) wordt:
e^x / (1+e^x)²
Zit ik een beetje correct of heb ik de plank compleet misgeslagen?
Ja en als ie hierna ook nog moet integreren...quote:Op zondag 11 mei 2014 22:41 schreef Riparius het volgende:
[..]
Ik ben benieuwd of iemand hier het vol gaat houden dit heerschap tot op de laatste dag voor zijn toets uitleg te blijven geven. Het moet alle respondenten hier nu toch wel duidelijk zijn dat dit gelijk staat aan water naar de zee dragen.
Of het klopt weet ik niet, maar de teller heeft een standaardafgeleide.quote:
Zit ik een beetje correct of heb ik de plank compleet misgeslagen?
Dat klopt. e^x heeft als standaardafgeleide e^x, dus e^x' = e^x.quote:
[..]
Of het klopt weet ik niet, maar de teller heeft een standaardafgeleide.
Nee, hier gaat het fout. Je kent de rekenregels voor het werken met machten niet. Hint:quote:
e^x * ( 1+e^x) - e^x * ( e^x)
Het uitwerken van dit resulteert tot:
e^x + e^x² - e^x²
ap·aq = ap+q
Ja die staat ook in zijn post.quote:
[..]
Of het klopt weet ik niet, maar de teller heeft een standaardafgeleide.
Ziet er goed uit.quote:
Zit ik een beetje correct of heb ik de plank compleet misgeslagen?
-edit- behalve dat foute die Riparius ziet.
Wat je ook had kunnen doe is
e^x / (1 + e^x ) = 1 / (e^{-x} + 1) = (e^{-x} + 1)^-1
Neem je daar de afgeleide van dan krijg je
-(e^{-x} + 1)^-2 * -e^{-x} = e^{-x} (e^{-x} + 1)^-2
Zit niet in de examenstofquote:
[..]
Ja en als ie hierna ook nog moet integreren...
http://www.eur.nl/fileadm(...)au_2_versie_2014.pdf
Ook een handige. Dankjewel!quote:
[..]
Ja die staat ook in zijn post.
[..]
Ziet er goed uit.
Wat je ook had kunnen doe is
e^x / (1 + e^x ) = 1 / (e^{-x} + 1) = (e^{-x} + 1)^-1
Neem je daar de afgeleide van dan krijg je
-(e^{-x} + 1)^-2 * -e^{-x} = e^{-x} (e^{-x} + 1)^-2
Dit was ook zowat de enige vraag waarover ik twijfelde bij de paragraaf differentiëren.
Volgende paragraaf is wel klote lijkt mij, maar het is wel het laatste 'onbekende'' onderwerp voor mij: Differentieerbaarheid.
Kijk nog wel even naar de opmerking van Riparius.quote:
[..]
Ook een handige. Dankjewel!
Dit was ook zowat de enige vraag waarover ik twijfelde bij de paragraaf differentiëren.
Volgende paragraaf is wel klote lijkt mij, maar het is wel het laatste 'onbekende'' onderwerp voor mij: Differentieerbaarheid.
Dank voor de attentie. Heb niet gezien wat ik fout deed. Want ik deed het wel goed toch?quote:
[..]
Kijk nog wel even naar de opmerking van Riparius.
Nee. Kijk nog eens naar Riparius post.quote:
[..]
Dank voor de attentie. Heb niet gezien wat ik fout deed. Want ik deed het wel goed toch?
-weg- Mag niet van thormodoquote:
[..]
Dank voor de attentie. Heb niet gezien wat ik fout deed. Want ik deed het wel goed toch?
Waarom geef je hem het antwoord nu gelijk? Als hij a.d.v. de rekenregels zelf moet uitvogelen wat hij fout doet leert hij daar veel meer van. Daarnaast blijft het dan veel beter hangen.quote:
Het is ook een beetje een notatieprobleem, maar als je e^x² schrijft dan betekent dat e-tot-de-macht-x-kwadraat en niet e-tot-de-macht-x-en-dat-weer-in-het-kwadraat. Dat laatste zou je namelijk moeten noteren als (e^x)^2 als je dan toch per se carets wil gebruiken. Maar, mijn advies: gebruik nu gewoon superscript. En geen smoesjes dat je een mobieltje gebruikt of zo, want daarmee gaat het ook.quote:
[..]
Dank voor de attentie. Heb niet gezien wat ik fout deed. Want ik deed het wel goed toch?
Ik weet niet hoe ik een superscript moet maken.quote:
[..]
Het is ook een beetje een notatieprobleem, maar als je e^x² schrijft dan betekent dat e-tot-de-macht-x-kwadraat en niet e-tot-de-macht-x-en-dat-weer-in-het kwadraat. Dat laatste zou je namelijk moeten noteren als (e^x)^2 als je dan toch per se carets wil gebruiken. Maar, mijn advies: gebruik nu gewoon superscript. En geen smoesjes dat je een mobieltje gebruikt of zo, want daarmee gaat het ook.
Ik denk dat het dan e^2x moet zijn. Want ik heb mijzelf in de tuin geleidt door anders te denken. Als ik dat nu zou opschrijven, zouden jullie mij niet kunnen volgen denk ik.
Je gebruikt zelfs superscript in je posts en als je quote kun je het commando ook zienquote:
[..]
Ik weet niet hoe ik een superscript moet maken.
Ik denk dat het dan e^2x moet zijn. Want ik heb mijzelf in de tuin geleidt door anders te denken. Als ik dat nu zou opschrijven, zouden jullie mij niet kunnen volgen denk ik.
. Dus e(sup)2x(/sup) , maar dan met blokhaken [ ].En als je de rekenregels netjes toepast hoef je niet te "denken", maar kun je het gewoon zeker weten
.
Ik wil dit topic niet overdonderen met vragen. Echter heb ik nog een vraag, mits jullie bereid zijn deze te beantwoorden:quote:
[..]
Je gebruikt zelfs superscript in je posts en als je quote kun je het commando ook zien
Hoe differentieer ik functies met de e waarde? Zoals
e(2x+1)
Superscript kun je op twee manieren krijgen:quote:
[..]
Ik weet niet hoe ik een superscript moet maken.
Ik denk dat het dan e^2x moet zijn. Want ik heb mijzelf in de tuin geleidt door anders te denken. Als ik dat nu zou opschrijven, zouden jullie mij niet kunnen volgen denk ik.
Eerste manier:
Datgene wat je wil superscripten met de muis selecteren (highlighten) en dan in het edit menu de button x² aanklikken.
Tweede manier:
| 1 | Laat hetgeen je wil superscripten vooraf gaan door [sup] en volgen door [/sup] |
Dank! Zie mijn post boven jouw post. Superscript is gelukt.quote:
[..]
Superscript kun je op twee manieren krijgen:
Eerste manier:
Datgene wat je wil superscripten met de muis selecteren (highlighten) en dan in het edit menu de button x² aanklikken.
Tweede manier:
[ code verwijderd ]
Door de kettingregel toe te passenquote:
[..]
Hoe differentieer ik functies met de e waarde? Zoals
e(2x+1)
.
Dit hem juist. Ik zou denken om 2x+1 als g(x) te benaderen en e als f(x), echter staat er gewoon e en geen e x .quote:
Raak er een beetje verward door.
Eerste wat mij te binnen schiet is:
2e2
Hint:quote:
[..]
Dit hem juist. Ik zou denken om 2x+1 als g(x) te benaderen en e als f(x), echter staat er gewoon e en geen e x .
Raak er een beetje verward door.
ex blijft gewoon hetzelfde als afgeleide.quote:
ex * 2x+1 * e2x
Dit wordt:
ex * 2x+1 * 2ex
2e 3+3x
Dit is hartstikke fout denk ik.
[ Bericht 2% gewijzigd door Super-B op 11-05-2014 23:24:09 ]
f(x)' (g(x)) is toch de afgeleide van functie f(x) vermenigvuldigt met de functie g(x)?quote:
Ik kom er eerlijk gezegd niet uit.
Heb je enig idee wat een compositie(/samenstelling) van functies is? Zo nee, dan moet je nog helemaal niet bezig houden met de kettingregel.
Kettingregel ging wel goed tot nu toe. De notatie is mij niet geheel duidelijk en het differentiëren met het getal e.quote:
Heb je enig idee wat een compositie(/samenstelling) van functies is? Zo nee, dan moet je nog helemaal niet bezig houden met de kettingregel.
Als ik niet wist ik hoe ik de kettingregel moest toepassen, was ik denk ik al tegen de muur aangelopen.
Het is gelukt dankjewel.
Tenslotte nog één vraag voordat ik ga slapen.
De afgeleide van:
ln (1 - 2x)
Ik deed
ln (1-2x) + ln (1-2x) --> afgeleide van de haakjes aan de rechterkant is -2.
Dus:
ln(1-2x) + ln -2
Daarna:
1 / (1-2x) + (1/x) -2
Dit wordt:
1 / (1-2x) + (-2x) / x
Ik doe iets fout, dat weet ik zeker.
Uitleg beetje kort door de bocht, excuus daarvoor.
Tenslotte nog één vraag voordat ik ga slapen.
De afgeleide van:
ln (1 - 2x)
Ik deed
ln (1-2x) + ln (1-2x) --> afgeleide van de haakjes aan de rechterkant is -2.
Dus:
ln(1-2x) + ln -2
Daarna:
1 / (1-2x) + (1/x) -2
Dit wordt:
1 / (1-2x) + (-2x) / x
Ik doe iets fout, dat weet ik zeker.
Uitleg beetje kort door de bocht, excuus daarvoor.
ln is een operator, dus ln (1-2x) is niet ln * (1-2x) maar ln(1-2x).quote:
Het is gelukt dankjewel.
Tenslotte nog één vraag voordat ik ga slapen.
De afgeleide van:
ln (1 - 2x)
Ik deed
ln * (1-2x) + ln (1-2x) --> afgeleide van de haakjes aan de rechterkant is -2.
Bewerkt.quote:
[..]
ln is een operator, dus ln (1-2x) is niet ln * (1-2x) maar ln(1-2x).
Wat doe ik fout?
ln(1-2x) = 2 ln(1-2x) ? = 2 (ln(1-2x) + ln(1-2x)) = 4 ln(1-2x)?quote:ln (1 - 2x)
Ik deed
ln (1-2x) + ln (1-2x)
yey gratis getallen
-edit-
Nu mag jij weer de kettingregel toepassen.
Dit is een samengestelde functie. Je hebt eigenlijk twee functies f: x → 2x + 1 en g: u → eu waarbij op een variabele x eerst f wordt toegepast en op het resultaat 2x + 1 = u daarvan weer g. Als je je een functie voorstelt als een black box waar je iets in stopt en waar dan ook weer iets uitkomt, dan heb je hier dus twee black boxes f en g, waarbij je de output van de eerste functie f gebruikt als input voor de tweede functie g. Schematisch voorgesteld:quote:
[..]
Ik wil dit topic niet overdonderen met vragen. Echter heb ik nog een vraag, mits jullie bereid zijn deze te beantwoorden:
Hoe differentieer ik functies met de e waarde? Zoals
e(2x+1)
x → 2x+1 → e2x+1
of, als we het 'tussenresultaat' 2x + 1 even voorstellen door de letter u en de functiewaarde e2x+1 zoals te doen gebruikelijk door de letter y:
x → u → y
Een afgeleide is eigenlijk niets anders dan wat in het Engels zo mooi kan worden uitgedrukt met de term rate of change. De afgeleide van een functie in een bepaald punt (i.e. voor een bepaalde waarde van x) vertelt ons hoe snel de functiewaarde op dat punt verandert in verhouding tot een verandering van x. Grafisch is de afgeleide zo niets anders dan de steilheid van de raaklijn aan de grafiek van de functie in dat punt.
De steilheid van zo'n raaklijn in een punt op de grafiek van een functie f berekenen we in wezen door naast het punt (x; f(x)) op de grafiek waar het ons om te doen is nog een tweede punt op de grafiek te nemen dat hier heel dicht bij in de buurt ligt, en dan te kijken wat er gebeurt met de steilheid van de snijlijn door deze twee punten als we dat tweede punt langs de grafiek naar het eerste punt toe laten bewegen.
Als je die x een klein beetje in waarde verandert, zodat we x+h krijgen, waarin h dus een getal voorstelt (positief óf negatief!) dat heel dicht bij nul ligt, dan heeft het tweede punt op onze grafiek de coördinaten (x+h; f(x+h)).
Om nu de steilheid (richtingscoëfficiënt) van de snijlijn door de punten (x; f(x)) en (x+h; f(x+h)) te krijgen, moeten we het hoogteverschil
Δy = f(x+h) − f(x)
tussen deze twee punten delen door de horizontale afstand
Δx = h
tussen deze twee punten, zodat we voor de steilheid van onze snijlijn door de punten (x; f(x)) en (x+h ; f(x+h)) dus krijgen
Δy/Δx = (f(x+h) − f(x))/h
Maar nu zijn we niet geïnteresseerd in de steilheid van de snijlijn door de punten (x; f(x)) en (x+h ; f(x+h)) maar in de steilheid van de raaklijn aan de grafiek in het punt (x; f(x)) en die vinden we door te kijken wat er gebeurt als we dat tweede punt (x+h ; f(x+h)) op onze grafiek steeds dichter naar het eerste punt (x; f(x)) laten gaan, dus als we h steeds dichter naar nul toe laten gaan.
We kunnen niet simpelweg h = 0 invullen in de formule voor Δy/Δx, want dan krijgen we 0/0 en dat heeft geen betekenis. Daarom moeten we met het begrip limiet werken. Limiet komt van het Latijnse woord limes (genitief limitis) dat 'grens' betekent. Een limiet is niets anders dan een grenswaarde waar we zo dicht bij in de buurt kunnen komen als we maar willen, als we een variabele (hier: h) maar dicht genoeg bij een bepaalde waarde (hier: nul) laten komen. Voor de afgeleide f'(x) van f(x) en daarmee de steilheid van de raaklijn aan de grafiek van f in een willekeurig punt (x; f(x)) op de grafiek hebben we dan
f'(x) = limh→0 (f(x+h) − f(x))/h
We kunnen dit ook anders noteren, de limiet van het quotiënt Δy/Δx als we Δx naar nul laten gaan wordt ook voorgesteld door dy/dx, dus
dy/dx = limΔx→0 Δy/Δx
Maar nu terug naar onze samengestelde functie, die we hierboven schematisch hadden voorgesteld als
x → u → y
We zijn nu geïnteresseerd in de rate of change van y ten opzichte van x, dus de snelheid waarmee y verandert in verhouding tot een verandering van x bij een gegeven uitgangswaarde van x, want dat is immers de steilheid van de raaklijn aan de grafiek voor een gegeven waarde van x.
Welnu, volgens de rekenregels voor breuken heb je
Δy/Δx = Δy/Δu · Δu/Δx
Maar dit stelt een steilheid voor van een snijlijn door twee punten op de grafiek, dus moeten we weer de limiet nemen voor Δx → 0. Aangezien Δu ook naar nul toe gaat als we Δx naar nul laten gaan geeft dit
limΔx→0 Δy/Δx = limΔu→0 Δy/Δu · limΔx→0 Δu/Δx
en dus
dy/dx = dy/du · du/dx
Dit is de kettingregel in de notatie van Leibniz. De kettingregel wordt ook vaak gegeven in een andere notatie, van Lagrange. We hebben hier u = f(x) en y = g(u) zodat y = g(f(x)). Nu is dy/du = g'(u) = g'(f(x)) en du/dx = f'(x) zodat we voor de afgeleide van g(f(x)) naar x dus hebben
g'(f(x))·f'(x)
In deze vorm is de kettingregel minder 'transparant' en intuïtief dan in de vorm van Leibniz, zodat het aanbeveling verdient om de kettingregel ook in de vorm van Leibniz te onthouden en te leren gebruiken.
Nu gaan we de kettingregel toepassen op onze samengestelde functie. We hadden
u = 2x + 1
en dat geeft
du/dx = 2
en verder hadden we
y = eu
en dat geeft
dy/du = eu
en dus vinden we
dy/dx = dy/du · du/dx = eu·2 = 2·eu = 2·e2x+1
In de praktijk is het na een beetje oefening heel goed mogelijk - en ook de bedoeling - om de afgeleide van een samengestelde functie direct op te schrijven zonder expliciet met de 'tussenvariabele' u te werken. We hebben hier y = e2x+1 en u = 2x+1 en als je dit invult in de kettingregel dy/dx = dy/du · du/dx dan heb je dus
d(e2x+1)/dx = d(e2x+1)/d(2x+1) · d(2x+1)/dx = e2x+1·2 = 2·e2x+1.
[ Bericht 0% gewijzigd door Riparius op 12-05-2014 03:30:06 ]
Dankje! Zeer heldere en duidelijke uitleg. Er zijn echter wat vraagtekens:quote:
[..]
Dit is een samengestelde functie. Je hebt eigenlijk twee functies f: x → 2x + 1 en g: u → eu waarbij op een variabele x eerst f wordt toegepast en op het resultaat 2x + 1 = u daarvan weer g. Als je je een functie voorstelt als een black box waar je iets in stopt en waar dan ook weer iets uitkomt, dan heb je hier dus twee black boxes f en g, waarbij je de output van de eerste functie f gebruikt als input voor de tweede functie g. Schematisch voorgesteld:
x → 2x+1 → e2x+1
of, als we het 'tussenresultaat' 2x + 1 even voorstellen door de letter u en de functiewaarde e2x+1 zoals te doen gebruikelijk door de letter y:
x → u → y
Een afgeleide is eigenlijk niets anders dan wat in het Engels zo mooi kan worden uitgedrukt met de term rate of change. De afgeleide van een functie in een bepaald punt (i.e. voor een bepaalde waarde van x) vertelt ons hoe snel de functiewaarde op dat punt verandert in verhouding tot een verandering van x. Grafisch is de afgeleide zo niets anders dan de steilheid van de raaklijn aan de grafiek van de functie in dat punt.
De steilheid van zo'n raaklijn in een punt op de grafiek van een functie f berekenen we in wezen door naast het punt (x; f(x)) op de grafiek waar het ons om te doen is nog een tweede punt op de grafiek te nemen dat hier heel dicht bij in de buurt ligt, en dan te kijken wat er gebeurt met de steilheid van de snijlijn door deze twee punten als we dat tweede punt langs de grafiek naar het eerste punt toe laten bewegen.
Als je die x een klein beetje in waarde verandert, zodat we x+h krijgen, waarin h dus een getal voorstelt (positief óf negatief!) dat heel dicht bij nul ligt, dan heeft het tweede punt op onze grafiek de coördinaten (x+h; f(x+h)).
Om nu de steilheid (richtingscoëfficiënt) van de snijlijn door de punten (x; f(x)) en (x+h; f(x+h)) te krijgen, moeten we het hoogteverschil
Δy = f(x+h) − f(x)
tussen deze twee punten delen door de horizontale afstand
Δx = h
tussen deze twee punten, zodat we voor de steilheid van onze snijlijn door de punten (x; f(x)) en (x+h ; f(x+h)) dus krijgen
Δy/Δx = (f(x+h) − f(x))/h
Maar nu zijn we niet geïnteresseerd in de steilheid van de snijlijn door de punten (x; f(x)) en (x+h ; f(x+h)) maar in de steilheid van de raaklijn aan de grafiek in het punt (x; f(x)) en die vinden we door te kijken wat er gebeurt als we dat tweede punt (x+h ; f(x+h)) op onze grafiek steeds dichter naar het eerste punt (x; f(x)) laten gaan, dus als we h steeds dichter naar nul toe laten gaan.
We kunnen niet simpelweg h = 0 invullen in de formule voor Δy/Δx, want dan krijgen we 0/0 en dat heeft geen betekenis. Daarom moeten we met het begrip limiet werken. Limiet komt van het Latijnse woord limes (genitief limitis) dat 'grens' betekent. Een limiet is niets anders dan een grenswaarde waar we zo dicht bij in de buurt kunnen komen als we maar willen, als we een variabele (hier: h) maar dicht genoeg bij een bepaalde waarde (hier: nul) laten komen. Voor de afgeleide f'(x) van f(x) en daarmee de steilheid van de raaklijn aan de grafiek van f in een willekeurig punt (x; f(x)) op de grafiek hebben we dan
f'(x) = limh→0 (f(x+h) − f(x))/h
We kunnen dit ook anders noteren, de limiet van het quotiënt Δy/Δx als we Δx naar nul laten gaan wordt ook voorgesteld door dy/dx, dus
dy/dx = limΔx→0 Δy/Δx
Maar nu terug naar onze samengestelde functie, die we hierboven schematisch hadden voorgesteld als
x → u → y
We zijn nu geïnteresseerd in de rate of change van y ten opzichte van x, dus de snelheid waarmee y verandert in verhouding tot een verandering van x bij een gegeven uitgangswaarde van x, want dat is immers de steilheid van de raaklijn aan de grafiek voor een gegeven waarde van x.
Welnu, volgens de rekenregels voor breuken heb je
Δy/Δx = Δy/Δu · Δu/Δx
Maar dit stelt een steilheid voor van een snijlijn door twee punten op de grafiek, dus moeten we weer de limiet nemen voor Δx → 0. Aangezien Δu ook naar nul toe gaat als we Δx naar nul laten gaan geeft dit
limΔx→0 Δy/Δx = limΔu→0 Δy/Δu · limΔx→0 Δu/Δx
en dus
dy/dx = dy/du · du/dx
Dit is de kettingregel in de notatie van Leibniz. De kettingregel wordt ook vaak gegeven in een andere notatie, van Lagrange. We hebben hier u = f(x) en y = g(u) zodat y = g(f(x)). Nu is dy/du = g'(u) = g'(f(x)) en du/dx = f'(x) zodat we voor de afgeleide van g(f(x)) naar x dus hebben
g'(f(x))·f'(x)
In deze vorm is de kettingregel minder 'transparant' en intuïtief dan in de vorm van Leibniz, zodat het aanbeveling verdient om de kettingregel ook in de vorm van Leibniz te onthouden en te leren gebruiken.
Nu gaan we de kettingregel toepassen op onze samengestelde functie. We hadden
u = 2x + 1
en dat geeft
du/dx = 2
en verder hadden we
y = eu
en dat geeft
dy/du = eu
en dus vinden we
dy/dx = dy/du · du/dx = eu·2 = 2·eu = 2·e2x+1
In de praktijk is het na een beetje oefening heel goed mogelijk - en ook de bedoeling - om de afgeleide van een samengestelde functie direct op te schrijven zonder expliciet met de 'tussenvariabele' u te werken. We hebben hier y = e2x+1 en u = 2x+1 en als je dit invult in de kettingregel dy/dx = dy/du · du/dx dan heb je dus
d(e2x+1)/dx = d(e2x+1)/d(2x+1) · d(2x+1)/dx = e2x+1·2 = 2·e2x+1.
Ik had hier ook nog eens naar gekeken:
Hier wordt dezelfde methode gebruikt (2:14) , echter wordt dy/du hier afgeleid direct van (p)³ naar 3p², terwijl jij in jouw quote echter alleen een variabele toewijst, dus in dit geval u = 2x + 1 en dan is dat dan eu
[ Bericht 0% gewijzigd door Super-B op 12-05-2014 11:40:18 ]
Die kerel in die video doet hetzelfde als Riparius.quote:
[..]
Dankje! Zeer heldere en duidelijke uitleg. Er zijn echter wat vraagtekens:
Ik had hier ook nog eens naar gekeken:
Hier wordt dezelfde methode gebruikt (2:14) , echter wordt dy/du hier afgeleid direct van (p)³ naar 3p², terwijl jij in jouw quote echter alleen een variabele toewijst, dus in dit geval u = 2x + 1 en dan is dat dan eu
Alleen heeft Riparius er veel meer informatie voor je bij gegeven.
y = e^(2x+1)
neem p = 2x+1
dan y = e^p
dy/dp = e^p
dp/dx = 2
En vervolgens
dy/dx = dy/dp dp/dx = e^p 2 = 2 e^(2x+1)
Riparius doet precies hetzelfde maar gebruikt dan een u ipv p.
[ Bericht 4% gewijzigd door t4rt4rus op 12-05-2014 12:02:01 ]
Ow zo. Ja het is duidelijk.quote:Op maandag 12 mei 2014 11:55 schreef t4rt4rus het volgende:
[..]
Die kerel in die video doet hetzelfde als Riparius.
Alleen heeft Riparius er veel meer informatie voor je bij gegeven.
y = e^(2x+1)
neem p = 2x+1
dan y = e^p
dy/dp = e^p
dp/dx = 2
En vervolgens
dy/dx = dy/dp dp/dx = e^p 2 = 2 e^(2x+1)
Riparius doet precies hetzelfde maar gebruikt dan een u ipv p.
Hoe pas je deze methode toe op de afgeleide van natuurlijke logaritmen?
Bijvoorbeeld: ln( 1 - 2x)
Ik pas dan de kettinregel toe:
1/x (1-2x) * -2
Doe ik hier iets fouts of..?
Weet iemand hoe je de inhoud van een achthoek berekend? elke zijde heeft een lengte van 18 meter en een hoogte van 12 m. Ik denk dat het iets met integralen is waar is heel slecht in ben..
Een achthoek heeft geen inhoud. De juiste benaming is een prisma.quote:
Weet iemand hoe je de inhoud van een achthoek berekend? elke zijde heeft een lengte van 18 meter en een hoogte van 12 m. Ik denk dat het iets met integralen is waar is heel slecht in ben..
Ken je de formule en/of aanpak voor het berekenen van de inhoud van een prisma?
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
Het is -2/(1-2x).quote:
[..]
Ow zo. Ja het is duidelijk.
Hoe pas je deze methode toe op de afgeleide van natuurlijke logaritmen?
Bijvoorbeeld: ln( 1 - 2x)
Ik pas dan de kettinregel toe:
1/x (1-2x) * -2
Doe ik hier iets fouts of..?
f(x) = ln(x)
u(x) = 1-2x
f(u(x))' = f'(u(x)) u'(x) = -2/(1-2x)
Nee het is geen prisma, ik moet de inhoud berekenen van de rotskoepel in Jeruzalem en het onderste deel is een achthoek, misschien zeg ik het verkeerd maar het is geen prisma :p de inhoud van de koepel heb ik ergens op internet al gevonden dus ik moet alleen nog de achthoek en het schuine 'dak' berekenen.quote:
[..]
Een achthoek heeft geen inhoud. De juiste benaming is een prisma.
Ken je de formule en/of aanpak voor het berekenen van de inhoud van een prisma?
En deze?quote:
[..]
Het is -2/(1-2x).
f(x) = ln(x)
u(x) = 1-2x
f(u(x))' = f'(u(x)) u'(x) = -2/(1-2x)
ln √(x+1)
Ik kom uit op :
1 / (√x+1) * 1/2x-1/2
Schrijf de stappen eens op, dan weet je waarschijnlijk ook of je het goed gedaan hebt.quote:
[..]
En deze?
ln √(x+1)
Ik kom uit op :
1 / (√x+1) * 1/2x-1/2
De stappen staan in mijn schrift. Ik schrijf alleen hier even het eindantwoord. Ik zal het even overnemen.. even wachten.quote:
[..]
Schrijf de stappen eens op, dan weet je waarschijnlijk ook of je het goed gedaan hebt.
Dit is letterlijk hoe ik het in mijn schrift heb opgenomen qua tussenstappen:quote:
[..]
Schrijf de stappen eens op, dan weet je waarschijnlijk ook of je het goed gedaan hebt.
ln √(x+1) --> functie
ln ( x + 1)1/2 ---> herschrijving
1/x * 1/2(x + 1) -1/2 --> afgeleide van ln en afgeleide van (x+1)1/2
1 / √(2x+2) --> herschrijving van de afgeleide
Duidelijkere stappen, schrijf op wat je subtitueert etc...quote:
[..]
Dit is letterlijk hoe ik het in mijn schrift heb opgenomen qua tussenstappen:
ln √(x+1) --> functie
ln ( x + 1)1/2 ---> herschrijving
1/x * 1/2(x + 1) -1/2 --> afgeleide van ln en afgeleide van (x+1)1/2
1 / √(2x+2) --> herschrijving van de afgeleide
Zoals het vorige voorbeeld
quote:y = e^(2x+1)
neem p = 2x+1
dan y = e^p
dy/dp = e^p
dp/dx = 2
En vervolgens de kettingregel toepassen
dy/dx = dy/dp dp/dx = e^p 2 = 2 e^(2x+1)
ln √(x+1) --> functiequote:
[..]
Duidelijkere stappen, schrijf op wat je subtitueert etc...
Zoals het vorige voorbeeld
[..]
ln ( x + 1)^1/2 ---> √(x+1) herschrijven tot ( x + 1)^1/2
1/x * 1/2(x + 1)^-1/2 --> afgeleide van ln opschrijven ( ln' = 1/x ), dat vermenigvuldigen met de afgeleide van ( x + 1)^1/2 en dat is 1/2(x + 1)^-1/2
1 / 2√(x+1) --> 1/2(x + 1)^-1/2 kan onder de deelstreep van 1/x vanwege -1/2 en de 1/2 wordt 2, aangezien het onder de deelstreep komt en dit wordt: 1 / 2√(x+1)
De inhoud heb je al op internet gevonden. Snap je die dan ook?quote:
[..]
Nee het is geen prisma, ik moet de inhoud berekenen van de rotskoepel in Jeruzalem en het onderste deel is een achthoek, misschien zeg ik het verkeerd maar het is geen prisma :p de inhoud van de koepel heb ik ergens op internet al gevonden dus ik moet alleen nog de achthoek en het schuine 'dak' berekenen.
Wat heb je al geprobeerd voor de oppervlakte van de achthoek en het dak?
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
Ik wil de kettingregel stappen zien.quote:
[..]
ln √(x+1) --> functie
ln ( x + 1)^1/2 ---> √(x+1) herschrijven tot ( x + 1)^1/2
1/x * 1/2(x + 1)^-1/2 --> afgeleide van ln opschrijven ( ln' = 1/x ), dat vermenigvuldigen met de afgeleide van ( x + 1)^1/2 en dat is 1/2(x + 1)^-1/2
1 / 2√(x+1) --> 1/2(x + 1)^-1/2 kan onder de deelstreep van 1/x vanwege -1/2 en de 1/2 wordt 2, aangezien het onder de deelstreep komt en dit wordt: 1 / 2√(x+1)
Zoals we met de vorige deden:
wat is y?
wat is p?
wat is de afgeleide van y naar p?
wat is de afgeleide van p naar x?
Gebruikmakend van de kettingregel wat is dan de afgeleide van y naar x?
y = ln √(x + 1)quote:
[..]
Duidelijkere stappen, schrijf op wat je subtitueert etc...
Zoals het vorige voorbeeld
[..]
neem p = √(x+1)
dan y = ln p
dy/dp = 1 / p
dp/dx = 1/2(x+1)^(-1/2)
En vervolgens de kettingregel toepassen
1 / p * 1/2(x+1)^(-1/2) = 1 / 2√(x+1)
Vrij ingewikkeld zoals je het doet. Het kan ook zonder logartime:quote:
[..]
ln √(x+1) --> functie
ln ( x + 1)^1/2 ---> √(x+1) herschrijven tot ( x + 1)^1/2
1/x * 1/2(x + 1)^-1/2 --> afgeleide van ln opschrijven ( ln' = 1/x ), dat vermenigvuldigen met de afgeleide van ( x + 1)^1/2 en dat is 1/2(x + 1)^-1/2
1 / 2√(x+1) --> 1/2(x + 1)^-1/2 kan onder de deelstreep van 1/x vanwege -1/2 en de 1/2 wordt 2, aangezien het onder de deelstreep komt en dit wordt: 1 / 2√(x+1)
1. Functie = √(x+1)
2. Vervang x+1 door p, dan krijg je f = √(p) = p1/2 met p = x+1
3. Nu differentieer je f en krijg je f' = 1/2 p-1/2 = 1 / 2√(p) = en differentieer je p en krijg je p' = 1
4. Terug invullen van wordt dan 1/2√(x+1) * 1 = 1/2√(x+1)
Op vrijdag 15 januari 2016 23:58 schreef Ajacied422 het volgende:
Feitelijk heeft Shreyas gewoon gelijk.
Feitelijk heeft Shreyas gewoon gelijk.
In je tweede regel staat wat p is...quote:
[..]
Ik heb geen idee... Als het 2 is dan kom ik uit op 4W(x+1)
Dus wat ben je hier dan aan het doen?quote:
Je vergeet het hele 1/p gedeelte.quote:1 / p * 1/2(x+1)^(-1/2) = 1 / 2√(x+1)
Blijf ik dan niet met een wortel hangen?quote:
[..]
Dus wat ben je hier dan aan het doen?
[..]
Je vergeet het hele 1/p gedeelte.
W(x+1) * W(x+1) ?
dy/dp = 1 / √(x+1)
dp/dx = 1/2√(x+1)
Vermenigvuldig die twee met elkaar (teller x teller en noemer x noemer) en je krijgt 1 / 2 √(x+1)√(x+1). Dan vervalt die wortel dus en krijg je 1 / 2(x+1) = 1 / 2x+2
dp/dx = 1/2√(x+1)
Vermenigvuldig die twee met elkaar (teller x teller en noemer x noemer) en je krijgt 1 / 2 √(x+1)√(x+1). Dan vervalt die wortel dus en krijg je 1 / 2(x+1) = 1 / 2x+2
Op vrijdag 15 januari 2016 23:58 schreef Ajacied422 het volgende:
Feitelijk heeft Shreyas gewoon gelijk.
Feitelijk heeft Shreyas gewoon gelijk.
Een wortel vervalt alleen als het dezelfde machtswortel is toch? Of moet de functie/getallen binnen de wortel ook hetzelfde zijn zodat het vervalt?quote:
dy/dp = 1 / √(x+1)
dp/dx = 1/2√(x+1)
Vermenigvuldig die twee met elkaar (teller x teller en noemer x noemer) en je krijgt 1 / 2 √(x+1)√(x+1). Dan vervalt die wortel dus en krijg je 1 / 2(x+1) = 1 / 2x+2
quote:
[..]
Een wortel vervalt alleen als het dezelfde machtswortel is toch? Of moet de functie/getallen binnen de wortel ook hetzelfde zijn zodat het vervalt?
√(16) = 4quote:
[..]
Een wortel vervalt alleen als het dezelfde machtswortel is toch? Of moet de functie/getallen binnen de wortel ook hetzelfde zijn zodat het vervalt?
√(16) x √(16) = 4 x 4 = 16
√(81) = 9
√(81) x √(81) = 9 x 9 = 81
√(25) x √(25) = 25
√(x) √(x) = x
√(x+1) √(x+1) = x+1
Op vrijdag 15 januari 2016 23:58 schreef Ajacied422 het volgende:
Feitelijk heeft Shreyas gewoon gelijk.
Feitelijk heeft Shreyas gewoon gelijk.
Hier gaat het weer fout.quote:
[..]
Duidelijkere stappen, schrijf op wat je subtitueert etc...
Zoals het vorige voorbeeld
[..]
ln x^(1/3)
y = ln x 1/3
p = x 1/3
dy/dp = 1 / x 1/3
dp/dx = 1/3x -2/3
dy/dx = (1/3)x -2/3 / x 1/3
Plaats die macht eens voor lnquote:
[..]
Hier gaat het weer fout.
ln x^(1/3)
y = ln x 1/3
p = x 1/3
dy/dp = 1 / x 1/3
dp/dx = 1/3x -2/3
dy/dx = (1/3)x -2/3 / x 1/3
zodat je krijgt
1/3 ln x
Kijk bij de logaritmische rekenregels waarom dit mag
Damn daar had ik ook helemaal niet aan gedacht.quote:
Het vorige probleem is dat nog makkelijker
Afgeleide is dan
-edit- maar goed hopelijk ken je de ketting regel nu ook veel beter.
Waar gaat die +1 naar toe?quote:
[..]
Damn daar had ik ook helemaal niet aan gedacht.
Het vorige probleem is dat nog makkelijker
Afgeleide is dan
Je krijgt sowieso
1 / 2*x maar mag die +1 ook onder de deelstreep komen als +1? Zo ja waarom?
Sorry moesten nog haakjes omheen.quote:
[..]
Waar gaat die +1 naar toe?
Je krijgt sowieso
1 / 2*x maar mag die +1 ook onder de deelstreep komen als +1? Zo ja waarom?
Aha oke..quote:
Als je
1/3 ln x doet, dan weet ik hoe ik hem moet afmaken, althans ik zie direct dat het 1/3x moet worden.
Maar hoe met het volgens de methode met dy/dx?
Ik krijg namelijk
y = 1/3 ln x
dy/dp = 1/x
dp / dx = 0 (1/3 is een constante)
Daar klopt natuurlijk niks van..
Je hebt daar ook geen functie compositie.quote:
[..]
Aha oke..
Als je
1/3 ln x doet, dan weet ik hoe ik hem moet afmaken, althans ik zie direct dat het 1/3x moet worden.
Maar hoe met het volgens de methode met dy/dx?
Ik krijg namelijk
y = 1/3 ln x
dy/dp = 1/x
dp / dx = 0 (1/3 is een constante)
Daar klopt natuurlijk niks van..
Dus daar kan je geen kettingregel toepassen.
nouja kan wel maar dat moet je de substitutie u = x gebruik, maar daar schiet je dus niks mee op.
of je kan de productregel gebruiken met een constant maar een constant mag je ook gelijk buiten de afleiding halen.
Hoi,
Ik zou graag willen differentieren en integreren. Ik heb oa de kettingregel, productregel en somregel al zien langskomen. Ik weet ook hoe een afgeleide gedefinieerd is, dat had te maken met de richtingscoefficient op een oneindig klein stukje lijn (limiet -> 0). 
Is het verstandig dit alleen te leren? Ik zit nu in 3 VWO, en naar mijn weten krijg je dit pas in 4/5 VWO...
Thx for the responses alvast!
Ik zou graag willen differentieren en integreren.
Ik heb oa de kettingregel, productregel en somregel al zien langskomen. Ik weet ook hoe een afgeleide gedefinieerd is, dat had te maken met de richtingscoefficient op een oneindig klein stukje lijn (limiet -> 0). Is het verstandig dit alleen te leren? Ik zit nu in 3 VWO, en naar mijn weten krijg je dit pas in 4/5 VWO...
Thx for the responses alvast!
Ik merk ik vastloop op het einde:
y = ln (1-x)1/3
p = (1-x)1/3
dy/dp = 1 / (1-x)1/3
dp/dx = 1/3(1-x)1/3
1 / (3(1-x)1/3 * (1-x)-2/3)
y = ln (1-x)1/3
p = (1-x)1/3
dy/dp = 1 / (1-x)1/3
dp/dx = 1/3(1-x)1/3
1 / (3(1-x)1/3 * (1-x)-2/3)
Ik ben hier niet helemaal zeker van, maar als je f(x) wilt differentieren met behulp van de kettingregel, dan zou ik zeggen g(x)=ln*x1/3 en dan u(x)=1-x.quote:
Ik merk ik vastloop op het einde:
y = ln (1-x)1/3
p = (1-x)1/3
dy/dp = 1 / (1-x)1/3
dp/dx = 1/3(1-x)1/3
1 / (3(1-x)1/3 * (1-x)-2/3)
f'(x)=g'(u(x))*u'(x)
g'(x)=1/(x1/3) = -2/3*x-5/3
u'(x)=-1
Ik hoop dat dit klopt, en als het klopt dan helpt het in ieder geval
EDIT: de afgeleide van f'(x) moet je nog zelf bedenken (antwoord)
Waarom niet eerst 1/3 wegwerken zoals op vorige pagina?quote:
Ik merk ik vastloop op het einde:
y = ln (1-x)1/3
p = (1-x)1/3
dy/dp = 1 / (1-x)1/3
dp/dx = 1/3(1-x)1/3
1 / (3(1-x)1/3 * (1-x)-2/3)
Ik heb het al. Thanks.quote:
Een compleet andere vraag binnen dit onderwerp:
Als ik de functie
m(x-a) / (x-a) = m heb, waarbij m de richtingscoëfficiënt van de raaklijn is, ofwel de afgeleide van de functie.
Een vergelijking van een niet-verticale raaklijn kan worden geschreven als y = f(a) + m(x-a)
Nou wil ik de vergelijking van de raaklijn bepalen aan de grafiek van f(x) in het punt (a, f(a)) in het volgende geval:
f(x) = 2x² - 3 waarbij a = 1
Ik dacht er dus aan om gewoon de vergelijking van de raaklijn hierbij te gebruiken en deze als het ware in te vullen f(a) + m(x-a) om zodoende x te berekenen en dan een formule te maken van f(a) + m(x-a).
Dus in dit geval
-De afgeleide van 2x³ - 3 = 4x
Dus f(a) + m(x-a) invullen wordt : 1 + 4x(x-1)
Klopt dit of zit ik compleet fout met mijn beredenering?
Wiskunde leren is nooit onverstandigquote:Op maandag 12 mei 2014 16:45 schreef netchip het volgende:
Hoi,
Ik zou graag willen differentieren en integreren.
Is het verstandig dit alleen te leren? Ik zit nu in 3 VWO, en naar mijn weten krijg je dit pas in 4/5 VWO...
Thx for the responses alvast!
. Wat kan je al? Je zegt dat je die regels voorbij hebt zien komen, maar kan je ze ook toepassen?
Leuk dat je wat van differentieren en integreren wil leren.
Let goed op dat je goede notatie gebruikt en dat je duidelijk schrijft wat je aan het doen bent.
En probeer het ook te begrijpen, dus niet zomaar een regeltje toepassen.
Dan kan je dat best wel lukken in VWO 3.
(Riparius vertelt straks wel dat ze dat vroeger ook al veel eerder kregen. )
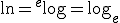, beide notatie worden wel gebruikt.
Waarvoor geldt dat
ln * x1/3] is dus niet toegestaan.
Het moet zijn ln x1/3 of ln(x1/3), dat laatste is wat duidelijker.
Verder doe je de substitutie u(x) = 1-x, wat je goed gezien hebt.
Maar die moet je dan ook doen in de function f(x), dan krijg je dus
f(u) = ln u1/3
Je hoeft hier denk ik niet perse een andere naam aan de functie te geven.
Dus je kan dit beter noteren als df/dx = df/du * du/dx
(of beter df(x)/dx = df(u(x))/du(x) * du(x)/dx)
Maar dat laatste is veel te veel schrijf werk
Je doet de substitutie u(x) = 1 - x en dan krijg je f(u) = ln(u1/3).
Hier kan je de kettingregel weer toepassen maar het is veel makkelijker om deze regel voor logaritmen te gebruiken
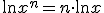
Dan krijgen we
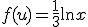
De afgeleide hiervan nemen is dat heel makkelijk
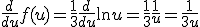
Constanten
[ Bericht 0% gewijzigd door t4rt4rus op 12-05-2014 18:18:21 ]
Let goed op dat je goede notatie gebruikt en dat je duidelijk schrijft wat je aan het doen bent.
En probeer het ook te begrijpen, dus niet zomaar een regeltje toepassen.
Dan kan je dat best wel lukken in VWO 3.
(Riparius vertelt straks wel dat ze dat vroeger ook al veel eerder kregen.
)ln is een operator. Het is het natuurlijk logaritme, logaritme met basis e.quote:
[..]
Ik ben hier niet helemaal zeker van, maar als je f(x) wilt differentieren met behulp van de kettingregel, dan zou ik zeggen g(x)=ln*x1/3 en dan u(x)=1-x.
Waarvoor geldt dat
ln * x1/3] is dus niet toegestaan.
Het moet zijn ln x1/3 of ln(x1/3), dat laatste is wat duidelijker.
Verder doe je de substitutie u(x) = 1-x, wat je goed gezien hebt.
Maar die moet je dan ook doen in de function f(x), dan krijg je dus
f(u) = ln u1/3
Je hoeft hier denk ik niet perse een andere naam aan de functie te geven.
Dit klopt inderdaad alleen is de notatie met ' onduidelijk als het gaat om waar je naar afleid.quote:f'(x)=g'(u(x))*u'(x)
Dus je kan dit beter noteren als df/dx = df/du * du/dx
(of beter df(x)/dx = df(u(x))/du(x) * du(x)/dx)
Maar dat laatste is veel te veel schrijf werk
Deze stap gaat fout.quote:g'(x)=1/(x1/3) = -2/3*x-5/3
Je doet de substitutie u(x) = 1 - x en dan krijg je f(u) = ln(u1/3).
Hier kan je de kettingregel weer toepassen maar het is veel makkelijker om deze regel voor logaritmen te gebruiken
Dan krijgen we
De afgeleide hiervan nemen is dat heel makkelijk
Constanten
En dan hoef je inderdaad alleen nog maar df/dx = df/du du/dx te doen.quote:u'(x)=-1
Ik hoop dat dit klopt, en als het klopt dan helpt het in ieder geval
EDIT: de afgeleide van f'(x) moet je nog zelf bedenken (antwoord)
[ Bericht 0% gewijzigd door t4rt4rus op 12-05-2014 18:18:21 ]
Is dit correct?quote:
En dan hoef je inderdaad alleen nog maar df/dx = df/du du/dx te doen.
d(ln(1-x)1/3) /dx
1/3* d(ln(1-x)) /dx
1/3* d(ln(1-x))/ d(1-x)* d(1-x)/ dx
1/3* 1/(1-x) *-1
Dat lijkt te kloppen.quote:
[..]
Is dit correct?
d(ln(1-x)1/3) /dx
1/3* d(ln(1-x)) /dx
1/3* d(ln(1-x))/ d(1-x)* d(1-x)/ dx
1/3* 1/(1-x) *-1
Dank je wel!quote:
Leuk dat je wat van differentieren en integreren wil leren.
Let goed op dat je goede notatie gebruikt en dat je duidelijk schrijft wat je aan het doen bent.
En probeer het ook te begrijpen, dus niet zomaar een regeltje toepassen.
Dan kan je dat best wel lukken in VWO 3.
(Riparius vertelt straks wel dat ze dat vroeger ook al veel eerder kregen.
[..]
ln is een operator. Het is het natuurlijk logaritme, logaritme met basis e.
Waarvoor geldt dat
[ afbeelding ]
ln * x1/3] is dus niet toegestaan.
Het moet zijn ln x1/3 of ln(x1/3), dat laatste is wat duidelijker.
Verder doe je de substitutie u(x) = 1-x, wat je goed gezien hebt.
Maar die moet je dan ook doen in de function f(x), dan krijg je dus
f(u) = ln u1/3
Je hoeft hier denk ik niet perse een andere naam aan de functie te geven.
[..]
Dit klopt inderdaad alleen is de notatie met ' onduidelijk als het gaat om waar je naar afleid.
Dus je kan dit beter noteren als df/dx = df/du * du/dx
(of beter df(x)/dx = df(u(x))/du(x) * du(x)/dx)
Maar dat laatste is veel te veel schrijf werk
[..]
Deze stap gaat fout.
Je doet de substitutie u(x) = 1 - x en dan krijg je f(u) = ln(u1/3).
Hier kan je de kettingregel weer toepassen maar het is veel makkelijker om deze regel voor logaritmen te gebruiken
Dan krijgen we
De afgeleide hiervan nemen is dat heel makkelijk
Constanten
[..]
En dan hoef je inderdaad alleen nog maar df/dx = df/du du/dx te doen.
Ik zal binnenkort naar de Leibniz-notatie kijken, want waar staat die 'd' voor? Differentiaal?
Wat is de tiende afgeleide van x^11? Mijn antwoord is (11*10*9*8*7*6*5*4*3*2)x
In het antwoordenmodel staat er 11!x.
Maar die 11! staat voor 11 faculteit en dat gaat door t/m *1, echter gaat het bij het tien keer afleiden van x^11 door tot *2 en niet tot *1 (zoals dat het geval is bij faculteit).
In het antwoordenmodel staat er 11!x.
Maar die 11! staat voor 11 faculteit en dat gaat door t/m *1, echter gaat het bij het tien keer afleiden van x^11 door tot *2 en niet tot *1 (zoals dat het geval is bij faculteit).
Maar iets vermenigvuldigen met 1 verandert toch niets.quote:
Wat is de tiende afgeleide van x^11? Mijn antwoord is (11*10*9*8*7*6*5*4*3*2)x
In het antwoordenmodel staat er 11!x.
Maar die 11! staat voor 11 faculteit en dat gaat door t/m *1, echter gaat het bij het tien keer afleiden van x^11 door tot *2 en niet tot *1 (zoals dat het geval is bij faculteit).
Weet ik, maar theoretisch gezien vind ik dat het geen 11! isquote:
[..]
Maar iets vermenigvuldigen met 1 verandert toch niets.
theoretisch is het precies hetzelfde.quote:
[..]
Weet ik, maar theoretisch gezien vind ik dat het geen 11! is
Maar goed laat jij maar 11*10*9*8*7*6*5*4*3*2 staan.
Nou als ik dat doe is het geheid fout op de toets.quote:
[..]
theoretisch is het precies hetzelfde.
Maar goed laat jij maar 11*10*9*8*7*6*5*4*3*2 staan.
De helling tussen twee punten is te berekenen metquote:
[..]
Dank je wel!
de verandering in y delen door de verandering in x.
Met de afgeleide neem je het limiet
Met de verandering van
Dat zou je inmiddels toch wel moeten weten, bedenk eens wat je recentelijk geleerd hebt en hoe je dat toe zou kunnen passen.quote:
Hoe kun je de intervallen bereken waarop een functie monotoon stijgend of dalend is?
Cuius rei demonstrationem mirabilem sane detexi hanc marginis exiguitas non caparet
Stijgend met een positieve ax en dalend met een negatieve ax.quote:Op maandag 12 mei 2014 19:25 schreef Diacetylmorfine het volgende:
[..]
Dat zou je inmiddels toch wel moeten weten, bedenk eens wat je recentelijk geleerd hebt en hoe je dat toe zou kunnen passen.
Verder weet ik dat een negatieve tweedegraadsverband een bergparabool is en een positieve tweedegraadsverband een dalparabool is.
Wat is een ax?quote:
[..]
Stijgend met een positieve ax en dalend met een negatieve ax.
Verder weet ik dat een negatieve tweedegraadsverband een bergparabool is en een positieve tweedegraadsverband een dalparabool is.
Waar is de ax vanquote:
[..]
De twee letters van een functie.. ax + b of ax² + bx + c
-edit-
Shit die is natuurlijk 1x
Maar goed die van
RustCohle snapt hier natuurlijk geen kloten van
Je beperkt je nu tot een klasse functies. Je weet wat de afgeleide is, hoe zou je de gevraagde informatie kunnen winnen uit de afgeleide?quote:
[..]
De twee letters van een functie.. ax + b of ax² + bx + c
Cuius rei demonstrationem mirabilem sane detexi hanc marginis exiguitas non caparet
