SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP


Het lijkt me allereerst handig dat je ons exact vertelt wat de opgave is. Met deze informatie is het zoals Riparius al stelde slechts mogelijk om uit te rekenen wat zijn gemiddelde snelheid was, en op mijn manier of hij niet minimaal 40 km/h diende te sprinten, wat dus niet het geval was omdat hij in 9,79 seconden meer dan 100 meter aflegde.
Dus wat was de extra randvoorwaarde, hoe nam zijn snelheid toe? Was daar een formule voor?
De afgeleide geeft de helling van een functie op een bepaald moment f'(x) = dy/dx Met dy en dx (infinitesimaal?) kleine verschillen. De quotiëntregel is te onthouden met (nat min tan) ofwel Noemer* afgeleide Teller - Teller * afgeleide Noemer (gedeeld door het kwadraat van de noemer). De kettingregel voor een functie f(x)*g(x) -> f'(x)*g(x)+g'(x)*f(x).
Om te weten waar de helling 0 is van een functie, ofwel het maximum/minimum van een grafiek stel je dus de afgeleide functie gelijk aan 0.
Om nu te weten waar de helling maximaal is geef je de tweede afgeleide, ofwel f''(x). Het nulpunt daarvan zal dus het buigpunt geven.
En nu die opgave.
Een klein voorbeeldje van de quotient regel:
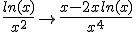
Je ziet zelf ook wel in dat dit nog een maal te vereenvoudigen is..
[ Bericht 7% gewijzigd door #ANONIEM op 23-06-2012 22:05:03 ]
Dus wat was de extra randvoorwaarde, hoe nam zijn snelheid toe? Was daar een formule voor?
De afgeleide geeft de helling van een functie op een bepaald moment f'(x) = dy/dx Met dy en dx (infinitesimaal?) kleine verschillen. De quotiëntregel is te onthouden met (nat min tan) ofwel Noemer* afgeleide Teller - Teller * afgeleide Noemer (gedeeld door het kwadraat van de noemer). De kettingregel voor een functie f(x)*g(x) -> f'(x)*g(x)+g'(x)*f(x).
Om te weten waar de helling 0 is van een functie, ofwel het maximum/minimum van een grafiek stel je dus de afgeleide functie gelijk aan 0.
Om nu te weten waar de helling maximaal is geef je de tweede afgeleide, ofwel f''(x). Het nulpunt daarvan zal dus het buigpunt geven.
En nu die opgave.
Een klein voorbeeldje van de quotient regel:
Je ziet zelf ook wel in dat dit nog een maal te vereenvoudigen is..
[ Bericht 7% gewijzigd door #ANONIEM op 23-06-2012 22:05:03 ]


Ik zal nog even toelichten wat ik hier precies doe. Ik gaf slechts de eerste stap.quote:Op zaterdag 23 juni 2012 21:54 schreef thenxero het volgende:
[..]
Ik zou zeggen
∫ sin(x)∙(-cos(x))' dx = -sin(x)∙cos(x) - ∫ -cos(x)∙(sin(x))' dx
[..]
De regel voor partieel integreren luidt:
∫ u∙dv = u∙v - ∫ v∙du
In dit geval hadden we u = sin(x), dv = sin(x)∙dx, en dus du = cos(x)∙dx, v = -cos(x). Dit geeft:
∫ sin(x)∙d(-cos(x)) = -sin(x)∙cos(x) - ∫ -cos(x)∙d(sin(x))
Nu volgt uit dv = sin(x)∙dx en v = -cos(x) dat d(-cos(x)) = sin(x)∙dx
Evenzo volgt uit du = cos(x)∙dx en u = sin(x) dat d(sin(x)) = cos(x)∙dx
Dus krijgen we:
∫ sin(x)∙sin(x)∙dx = -sin(x)∙cos(x) - ∫ -cos(x)∙cos(x)∙dx
En dus:
∫ sin2(x)∙dx = -sin(x)∙cos(x) + ∫ cos2(x)∙dx


En toch komen we allemaal op hetzelfde uit. Ik begrijp dat ik slechts de haakjes moet zetten, waar ik inderdaad wel vaker commentaar van die 'flutdocent' op heb gekregen.
Maar enfin, als Superky ook nog eens wil reageren binnen het uur..
Maar enfin, als Superky ook nog eens wil reageren binnen het uur..


Oh zo. Ik heb geleerd om die tussenstap over te slaan, omdat je dan met infinitesimalen werkt zonder bewijs.
Ik onthou die regel ook als ∫ f(x)g'(x) dx = f(x)g(x) - ∫ f'(x)g(x) dx .
[ Bericht 23% gewijzigd door thenxero op 23-06-2012 22:35:14 ]
Ik onthou die regel ook als ∫ f(x)g'(x) dx = f(x)g(x) - ∫ f'(x)g(x) dx .
[ Bericht 23% gewijzigd door thenxero op 23-06-2012 22:35:14 ]


Sorry voor de late reactie maar hier komt de opgave:quote:Op zaterdag 23 juni 2012 21:58 schreef Amoeba het volgende:
Het lijkt me allereerst handig dat je ons exact vertelt wat de opgave is. Met deze informatie is het zoals Riparius al stelde slechts mogelijk om uit te rekenen wat zijn gemiddelde snelheid was, en op mijn manier of hij niet minimaal 40 km/h diende te sprinten, wat dus niet het geval was omdat hij in 9,79 seconden meer dan 100 meter aflegde.
Dus wat was de extra randvoorwaarde, hoe nam zijn snelheid toe? Was daar een formule voor?
De afgeleide geeft de helling van een functie op een bepaald moment f'(x) = dy/dx Met dy en dx (infinitesimaal?) kleine verschillen. De quotiëntregel is te onthouden met (nat min tan) ofwel Noemer* afgeleide Teller - Teller * afgeleide Noemer (gedeeld door het kwadraat van de noemer). De kettingregel voor een functie f(x)*g(x) -> f'(x)*g(x)+g'(x)*f(x).
Om te weten waar de helling 0 is van een functie, ofwel het maximum/minimum van een grafiek stel je dus de afgeleide functie gelijk aan 0.
Om nu te weten waar de helling maximaal is geef je de tweede afgeleide, ofwel f''(x). Het nulpunt daarvan zal dus het buigpunt geven.
En nu die opgave.
Een klein voorbeeldje van de quotient regel:
Je ziet zelf ook wel in dat dit nog een maal te vereenvoudigen is..
Omrekenen van eenheden
Het wereldrecord op de 100 m hardlopen is kort geleden gebracht op 9,79 s. Heeft de atleet op enig moment gedurende zijn race met een snelheid groter dan 40 km per uur gelopen?
En verder staat er niks meer.


Dan kun je keihard zeggen dat je met behulp van de maximaal afgelegde afstand voor een snelheid van 40 km/h deze vraag niet kan beantwoorden. Dat zal dan ook wel het antwoord zijn.
Want:
40 km/h = 40/3,6 = 11,11 m/s * 9,79 > 100m. Ofwel dit is niet te beantwoorden met deze gegevens.
Want:
40 km/h = 40/3,6 = 11,11 m/s * 9,79 > 100m. Ofwel dit is niet te beantwoorden met deze gegevens.


Uiteraard sla ik de tussenstap gewoonlijk ook over, maar omdat Amoeba deze tussenstap toch maakte wilde ik even laten zien hoe je dat dan correct op kunt schrijven. Uitgaande van de regelquote:Op zaterdag 23 juni 2012 22:27 schreef thenxero het volgende:
Oh zo. Ik heb geleerd om die tussenstap over te slaan, omdat je dan met infinitesimalen werkt zonder bewijs.
Ik onthou die regel ook als ∫ f(x)g'(x) dx = f(x)g(x) - ∫ f'(x)g(x) dx .
∫ u∙dv = u∙v - ∫ v∙du
en
u = sin(x), dv = sin(x)∙dx, du = cos(x)∙dx, v = -cos(x)
krijg je direct
∫ sin(x)∙sin(x)∙dx = -sin(x)∙cos(x) - ∫ -cos(x)∙cos(x)∙dx
en dat is ook gebruikelijke manier van werken met de regel voor partieel integreren in deze vorm, zie bijvoorbeeld hier.
Werken met differentialen is niet hetzelfde als werken met infinitesimalen, dus hier is niets inexacts aan, vooropgesteld dat je een formele definitie kunt geven voor (betrekkingen tussen) differentialen die niet steunt op het intuïtieve begrip van 'oneindig kleine' grootheden. Vroeger was dat uiteraard anders, de gehele Leibniz notatie is gebaseerd op de idee van inifinitesimale grootheden.
Toch is de notatie van Leibniz niet stuk te krijgen en heeft deze alle paradigmawisselingen binnen de wiskunde overleefd, en daar zijn goede redenen voor. Deze notatie vereenvoudigt het werken met afgeleiden van samengestelde functies (kettingregel), het werken met de substitutieregel in de integraalrekening (en inderdaad, ook het werken met partieel integreren) en bijvoorbeeld ook het oplossen van bepaalde differentiaalvergelijkingen (scheiding van variabelen).
De substitutieregel (voor onbepaalde integralen) kunnen we weergeven als
∫ f(x)∙dx = ∫ f(g(t))∙g'(t)∙dt
waarbij x = g(t) en dx = g'(t)∙dt zodat d(g(t)) = g'(t)∙dt en we de substitutieregel dus ook kunnen weergeven als
∫ f(x)∙dx = ∫ f(g(t))∙d(g(t))
Als nu F een primitieve is van f dan is dus
∫ f(g(t))∙d(g(t)) = F(g(t)) + C
Hiervan maakte ik gebruik bij enkele herleidingen voor het primitiveren van de secans.
Hebben we f(x) = 1, zodat F(x) = x een primitieve is, dan reduceert dit tot:
∫ d(g(t)) = g(t) + C
zodat je, afgezien van de integratieconstante, kunt zeggen dat ∫ en d inverse operatoren zijn.
Als we hebben y = f(x) waarbij f een differentieerbare functie is van x, dan kunnen we zeggen dat dy/dx = f'(x), en als we het hierbij laten dan zijn dit gewoon twee verschillende notaties voor hetzelfde, namelijk de notatie van Leibniz en de notatie van Lagrange voor de (eerste) afgeleide van de gegeven functie. De uitdrukking dy/dx lijkt verdacht veel op een breuk en om de verwarring nog groter te maken heet dit ook nog een differentiaalquotiënt, terwijl het in de thans gebruikelijke opvatting geen quotiënt is maar een limiet van een differentiequotiënt ∆y/∆x = (f(x + ∆x) - f(x))/∆x voor ∆x → 0.
Maar zo hebben dy en dx afzonderlijk geen betekenis (meer), zodat je nog moet verantwoorden wat je dan precies verstaat onder dy = f'(x)∙dx en hoe dit equivalent is met dy/dx = f'(x) zonder daarbij terug te vallen op intuïtieve begrippen als 'oneindig kleine' grootheden. Er zijn verschillende manieren om het begrip differentiaal te formaliseren maar die zijn niet zo geschikt voor een elementaire behandeling. Je zou echter kunnen afspreken dat je met dy = f'(x)∙dx bedoelt dat de grootheid x (en daarmee ook y) afhangt van een andere variabele, zeg t, zodanig dat dy/dt = f'(x) ∙ dx/dt. Dan is dus y'(t) = f'(x)∙x'(t) oftewel y'(t) = f'(x(t))∙x'(t) en dat is niets anders dan de kettingregel voor y(t) = f(x(t)). Dit is altijd mogelijk, want we kunnen eenvoudig x(t) = t nemen. Betrekkingen tussen differentialen van grootheden kun je zo dus zien als betrekkingen tussen de afgeleiden van die grootheden waarbij de onafhankelijke variabele impliciet is.
We kunnen nu bijvoorbeeld schrijven d(u∙v) = du∙v + u∙dv waarbij u en v functies zijn van een impliciete variabele (i.e. als we deze impliciete variabele t noemen: d(u∙v)/dt = du/dt ∙ v + u ∙ dv/dt) en dit geeft dan ∫ d(u∙v) = ∫ du∙v + ∫ u∙dv en dus ∫ u∙dv = u∙v - ∫ v∙du aangezien ∫ d(u∙v) = u∙v, waarbij we de integratieconstante achterwege laten omdat deze al in ∫ v∙du zit.
[ Bericht 0% gewijzigd door Riparius op 24-06-2012 19:44:32 ]


Deze post kan dus ook in de bundel. En die tussenstap maak ik omdat ik anders sneller fouten maak.
[ Bericht 47% gewijzigd door #ANONIEM op 24-06-2012 19:26:32 ]
[ Bericht 47% gewijzigd door #ANONIEM op 24-06-2012 19:26:32 ]


Deze nog iemand tips?
Hoe laat ik zien dat:
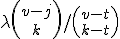
gelijk is aan
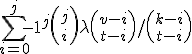
Achtergrond: beiden zijn uitdrukkingen voor het aantal blokken in een t-(v,k,lambda) design (X, B) dat geen punten overeenkomt met een j-subset van X, J.
De eerste uitdrukking komt van een dubbeltelargument het tweede van het gebruik van het principe van inclusie exclusie. Dit is het enige wat ik me nog afvraag, hoe je ze omschrijft in elkaar.
Hoe laat ik zien dat:
gelijk is aan
Achtergrond: beiden zijn uitdrukkingen voor het aantal blokken in een t-(v,k,lambda) design (X, B) dat geen punten overeenkomt met een j-subset van X, J.
De eerste uitdrukking komt van een dubbeltelargument het tweede van het gebruik van het principe van inclusie exclusie. Dit is het enige wat ik me nog afvraag, hoe je ze omschrijft in elkaar.


Als het beide uitdrukkingen zijn voor hetzelfde aantal, heb je daarmee bewezen dat ze gelijk aan elkaar zijn.


Ik had alleen die notatie nooit gezien, voor de rest ben ik volledig op de hoogte. Dat bewijs dat infinitesimalen bestaan is wel leuk, heb dat een keer gezien. Als het er was geweest had ik ook een vak nonstandaard analyse gedaanquote:


Als je de afgeleide van Fréchet gebruikt, hebben dy en dx wel gewoon een betekenis, net als dy/dx.quote:Op zondag 24 juni 2012 19:14 schreef Riparius het volgende:
[..]
Maar zo hebben dy en dx afzonderlijk geen betekenis (meer), zodat je nog moet verantwoorden wat je dan precies verstaat onder dy = f'(x)∙dx en hoe dit equivalent is met dy/dx = f'(x) zonder daarbij terug te vallen op intuïtieve begrippen als 'oneindig kleine' grootheden. Er zijn verschillende manieren om het begrip differentiaal te formaliseren maar die zijn niet zo geschikt voor een elementaire behandeling. Je zou echter kunnen afspreken dat je met dy = f'(x)∙dx bedoelt dat de grootheid x (en daarmee ook y) afhangt van een andere variabele, zeg t, zodanig dat dy/dt = f'(x) ∙ dx/dt. Dan is dus y'(t) = f'(x)∙x'(t) oftewel y'(t) = f'(x(t))∙x'(t) en dat is niets anders dan de kettingregel voor y(t) = f(x(t)). Dit is altijd mogelijk, want we kunnen eenvoudig x(t) = t nemen. Betrekkingen tussen differentialen van grootheden kun je zo dus zien als betrekkingen tussen de afgeleiden van die grootheden waarbij de onafhankelijke variabele impliciet is.


Het lijkt me toch dat je hier het een en ander wel kunt vereenvoudigen. Schrijf die binomiaalcoëfficiënten maar eens uit in faculteiten. In beide uitdrukkingen zie je dan al een (k-t)!/(v-t)! verschijnen, en in die onderste uitdrukking valt er in elke term een (t-i)! tegen elkaar weg.quote:Op zondag 24 juni 2012 19:47 schreef Oneironaut het volgende:
Deze nog iemand tips?
Hoe laat ik zien dat:
gelijk is aan
Achtergrond: beiden zijn uitdrukkingen voor het aantal blokken in een t-(v,k,lambda) design (X, B) dat geen punten overeenkomt met een j-subset van X, J.
De eerste uitdrukking komt van een dubbeltelargument het tweede van het gebruik van het principe van inclusie exclusie. Dit is het enige wat ik me nog afvraag, hoe je ze omschrijft in elkaar.


quote:Op zondag 24 juni 2012 19:47 schreef Oneironaut het volgende:
Deze nog iemand tips?
Hoe laat ik zien dat:
gelijk is aan
Achtergrond: beiden zijn uitdrukkingen voor het aantal blokken in een t-(v,k,lambda) design (X, B) dat geen punten overeenkomt met een j-subset van X, J.
De eerste uitdrukking komt van een dubbeltelargument het tweede van het gebruik van het principe van inclusie exclusie. Dit is het enige wat ik me nog afvraag, hoe je ze omschrijft in elkaar.
Het moest overigens zijn (macht i niet j):quote:Op zondag 24 juni 2012 20:52 schreef thabit het volgende:
[..]
Het lijkt me toch dat je hier het een en ander wel kunt vereenvoudigen. Schrijf die binomiaalcoëfficiënten maar eens uit in faculteiten. In beide uitdrukkingen zie je dan al een (k-t)!/(v-t)! verschijnen, en in die onderste uitdrukking valt er in elke term een (t-i)! tegen elkaar weg.
Dit is
Dus blijft over:
Oh en
Maar die som.... welke regel kan ik daar voor gebruiken?
Iets van: http://mathworld.wolfram.com/BinomialSums.html ?
[ Bericht 0% gewijzigd door Oneironaut op 24-06-2012 23:32:01 ]


Ik zou  laten staan, en
laten staan, en 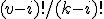 kun je schrijven als
kun je schrijven als 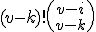 . De factor (v-k)! heb je ook in die eerste formule. Op die manier krijg je al een heel wat eenvoudigere identiteit die je moet bewijzen.
. De factor (v-k)! heb je ook in die eerste formule. Op die manier krijg je al een heel wat eenvoudigere identiteit die je moet bewijzen.


Als het goed is krijg je dus iets met de sommatie 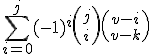 erin. Ga even na of dit klopt. Dit soort sommen zijn namelijk vrij algemeen uit te werken, als je het truukje weet.
erin. Ga even na of dit klopt. Dit soort sommen zijn namelijk vrij algemeen uit te werken, als je het truukje weet.


Nog maar een vraagje, want ik loop hier vast.
Hoe kom je op die 17,55% (onderste zin)? Want dat staat er niet bij.
Hoe kom je op die 17,55% (onderste zin)? Want dat staat er niet bij.


GR niet, dat laatste dan denk ik.quote:Op maandag 25 juni 2012 14:53 schreef thenxero het volgende:
Misschien met je GR, of met een normale benadering?


Met de normale benadering krijg ik 17.2%. Lijkt mij prima maar ik weet niet wat ze van je verwachten. Omdat exact te doen lijkt me vrij vervelend.


Kan zijn dat ze dan het gemiddelde hebben genomen van de normale benadering voor X = 11 en X = 10. Exact hoeft volgens mij niet.quote:Op maandag 25 juni 2012 15:32 schreef thenxero het volgende:
Met de normale benadering krijg ik 17.2%. Lijkt mij prima maar ik weet niet wat ze van je verwachten. Omdat exact te doen lijkt me vrij vervelend.


Het is echt een exact resultaat, lijkt me dus GR-werk of pc-werk.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Oh dan heeft de docent het met de GR gedaan denk ik. Maar dat mogen wij niet.quote:Op maandag 25 juni 2012 15:52 schreef GlowMouse het volgende:
Het is echt een exact resultaat, lijkt me dus GR-werk of pc-werk.


Simpel vraagje denk ik:
Wat heeft de waarde constant voor een betekenis in een logistic regression?
[ Bericht 17% gewijzigd door Soldier2000 op 25-06-2012 17:19:13 ]
Wat heeft de waarde constant voor een betekenis in een logistic regression?
[ Bericht 17% gewijzigd door Soldier2000 op 25-06-2012 17:19:13 ]
BlaBlaBla


bereken de odds ratio dan voor X=0quote:Op maandag 25 juni 2012 18:40 schreef Soldier2000 het volgende:
[..]
Ik ben opzoek naar de algemene betekenis van constant
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Je hoeft toch helemaal niets te berekenen om te weten wat de waarde constant wil zeggen in de bovenstaande tabel? Ik heb de data set namelijk niet.quote:
The response to the test mailing = -3.648 when X (M, R, F etc.) =0 ?
Is het niet zo dat de constante waarde wel onderdeel van de formule is, maar geen interpreteerbare betekenis heeft?
[ Bericht 12% gewijzigd door Soldier2000 op 25-06-2012 20:41:07 ]
BlaBlaBla


Nee, bereken de odds ratio symbolisch.quote:Op maandag 25 juni 2012 20:12 schreef Soldier2000 het volgende:
[..]
Is het niet zo dat de constante waarde wel onderdeel van de formule is, maar geen interpreteerbare betekenis heeft?dan weet ik namelijk al voldoende
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Het klinkt zo gemakkelijk, maar mijn statistiek is zo snel zo ver weggezaktquote:Op maandag 25 juni 2012 20:44 schreef GlowMouse het volgende:
[..]
Nee, bereken de odds ratio symbolisch.
BlaBlaBla


Dadelijk even m'n vorige vraag terug zoeken, m'n internet lag er een aantal dagen uit. Voor nu even een nieuwe vraag, maar zie me als een investering - wanneer mijn kennis op niveau is kom ik hier helpen.
Hoe bereken ik arctan (3/4) uit m'n hoofd? Een sinus of cosinus is gesneden koek, maar de tangens ligt me wat minder lekker.
Hoe bereken ik arctan (3/4) uit m'n hoofd? Een sinus of cosinus is gesneden koek, maar de tangens ligt me wat minder lekker.
"Social order at the expense of liberty is hardly a bargain."


Wolfram alpha geeft geen exact antwoord (dus die zal niet bestaan of vrij gecompliceerd zijn), dus je zult het dan moeten benaderen net zoals je rekenmachine dat doet. Je kan hiervoor een Taylorreeks gebruiken... die van de arctan convergeert heel snel dus na een aantal termen ben je wel klaar (vooral als x dichtbij 0 zit).quote:Op maandag 25 juni 2012 22:19 schreef Quir het volgende:
Dadelijk even m'n vorige vraag terug zoeken, m'n internet lag er een aantal dagen uit. Voor nu even een nieuwe vraag, maar zie me als een investering - wanneer mijn kennis op niveau is kom ik hier helpen.
Hoe bereken ik arctan (3/4) uit m'n hoofd? Een sinus of cosinus is gesneden koek, maar de tangens ligt me wat minder lekker.
Die snelle benadering geeft al arctan(3/4) = 0.656 terwijl het eigenlijk 0.643 is.
Sommige waarden kan je wel makkelijk exact berekenen, zoals arctan(1) of arctan(0) (probeer maar).


Ah, zo - nouja, de vraag in het boek was arccos(-arctan(3/4)), maar ik probeerde de bijbehorende hoek te vinden. Als dat niet zo makkelijk gaat, dan laat ik 't mooi zitten. En arctan 1 of 0 had ik al door ((pi/4) en 0). Dank voor je antwoord.
"Social order at the expense of liberty is hardly a bargain."


Misschien kan onze gonio-vriend Riparius je beter helpenquote:Op maandag 25 juni 2012 22:55 schreef Quir het volgende:
Ah, zo - nouja, de vraag in het boek was arccos(-arctan(3/4)), maar ik probeerde de bijbehorende hoek te vinden. Als dat niet zo makkelijk gaat, dan laat ik 't mooi zitten. En arctan 1 of 0 had ik al door ((pi/4) en 0). Dank voor je antwoord.


Weet je zeker dat er niet naar cos(-arctan(3/4)) wordt gevraagd?quote:Op maandag 25 juni 2012 22:55 schreef Quir het volgende:
Ah, zo - nouja, de vraag in het boek was arccos(-arctan(3/4)), maar ik probeerde de bijbehorende hoek te vinden. Als dat niet zo makkelijk gaat, dan laat ik 't mooi zitten. En arctan 1 of 0 had ik al door ((pi/4) en 0). Dank voor je antwoord.


Gevraagd om te berekenen:
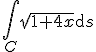 met C een curve in
met C een curve in 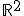 en
en 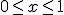 ,
, 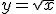
Mijn berekening:
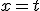 ,
, 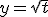 dus
dus 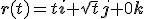 en dus
en dus 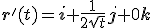
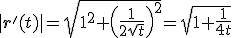
dus de integraal wordt: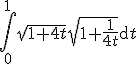
Klopt dit tot hier?
Mijn berekening:
dus de integraal wordt:
Klopt dit tot hier?


Ja, maar je maakt het jezelf onnodig moeilijk. Je heb namelijk:quote:Op dinsdag 26 juni 2012 00:22 schreef Dale. het volgende:
Gevraagd om te berekenen:met C een curve in
en
,
Mijn berekening:,
dus
en dus
dus de integraal wordt:
Klopt dit tot hier?
ds = (dx2 + dy2)1/2 = (1 + (dy/dx)2)1/2∙dx
en aangezien dy/dx = ½∙x-1/2 krijg je dan meteen de integraal die je geeft, maar dan met x als variabele.


Oke de integraal klopt dus. Maar dan hoe reken ik deze uit? Wolfram geeft http://www.wolframalpha.com/input/?i=int+sqrt%281+%2B+4*t%29+*+sqrt%281+%2B+1%2F%284*t%29%29+dt maar daar begrijp ik de stap niet van 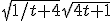 naar
naar 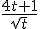 niet. De integraal moet simpeler op te lossen zijn toch ook trouwens?
niet. De integraal moet simpeler op te lossen zijn toch ook trouwens?


Het is beter om gebruik te maken van:quote:Op maandag 25 juni 2012 22:30 schreef thenxero het volgende:
[..]
Wolfram alpha geeft geen exact antwoord (dus die zal niet bestaan of vrij gecompliceerd zijn), dus je zult het dan moeten benaderen net zoals je rekenmachine dat doet. Je kan hiervoor een Taylorreeks gebruiken... die van de arctan convergeert heel snel dus na een aantal termen ben je wel klaar (vooral als x dichtbij 0 zit).
Die snelle benadering geeft al arctan(3/4) = 0.656 terwijl het eigenlijk 0.643 is.
Sommige waarden kan je wel makkelijk exact berekenen, zoals arctan(1) of arctan(0) (probeer maar).
arctan(3/4) = 2∙arctan(1/3)
aangezien de reeks (zoals je zelf opmerkt) sneller convergeert naarmate x dichter bij 0 ligt.
Dan krijg je:
arctan(3/4) ≈ 2∙(1/3 - (1/3)3/3 + (1/3)5/5) = 782/1215 = 0,6436 ...
Nog veel beter wordt het als je gebruik maakt van
arctan(3/4) = π/4 - arctan(1/7)
Aangezien we niet eerst een benadering voor π uit willen rekenen (waarvoor we ook weer een reeksontwikkeling nodig zouden hebben) maken we hiervoor gebruik van de benadering 355/113 (het getal van Metius). Dan krijgen we:
arctan(3/4) ≈ (1/4)∙(355/113) - (1/7 - (1/7)3/3 + (1/7)5/5) = 0,643501...
En zie daar, we hebben arctan(3/4) in zes decimalen nauwkeurig.
[ Bericht 15% gewijzigd door Riparius op 26-06-2012 03:32:50 ]


Je moet niet meteen je probleem in WolframAlpha (of een ander computeralgebra systeem) stoppen en dan proberen dat slaafs na te doen met pen en papier. Een mens is nog altijd creatiever dan een computer (maar jij kennelijk niet ...).quote:Op dinsdag 26 juni 2012 00:45 schreef Dale. het volgende:
Oke de integraal klopt dus. Maar dan hoe reken ik deze uit? Wolfram geeft http://www.wolframalpha.com/input/?i=int+sqrt%281+%2B+4*t%29+*+sqrt%281+%2B+1%2F%284*t%29%29+dt maar daar begrijp ik de stap niet vannaar
niet. De integraal moet simpeler op te lossen zijn toch ook trouwens?
Ik ga eerst je integrand in een wat hanteerbaarder vorm brengen. We hebben:
√(1 + 4t)∙√(1 + 1/(4t)) = √(1 + 1/(4t) + 4t + 1) = √(4t + 2 + 1/(4t))
Nu gaan we de termen onder het wortelteken onder één noemer brengen. Dit geeft:
4t + 2 + 1/(4t) = (16t2 + 8t + 1)/(4t) = (4t + 1)2/(4t)
Dus krijgen we:
√(4t + 2 + 1/(4t)) = (4t + 1)∙(4t)-1/2 = ½∙(4t + 1)∙t-1/2 = 2∙t1/2 + ½∙t-1/2
De integraal wordt nu:
∫01 (2∙t1/2 + ½∙t-1/2)∙dt = [(4/3)∙t3/2 + t1/2]01 = 4/3 + 1 = 7/3.
[ Bericht 0% gewijzigd door Riparius op 26-06-2012 02:33:30 ]


Volgens mij zou het rekenmachine het ook niet eens zijn met arccos(-arctan(3/4)), dus, ja, het moest inderdaad cos zijn. Foutje.quote:Op dinsdag 26 juni 2012 00:05 schreef Riparius het volgende:
[..]
Weet je zeker dat er niet naar cos(-arctan(3/4)) wordt gevraagd?
"Social order at the expense of liberty is hardly a bargain."


Je begrijpt er kennelijk nog niet veel van, want -arctan(3/4) ligt tussen -π/4 en 0 en daarmee binnen het domein [-1,1] van de (reële) arcus cosinus functie, zodat arccos(-arctan(3/4)) gewoon (numeriek) is te bepalen.quote:Op dinsdag 26 juni 2012 11:50 schreef Quir het volgende:
[..]
Volgens mij zou de rekenmachine het ook niet eens zijn met arccos(-arctan(3/4)), dus, ja, het moest inderdaad cos zijn. Foutje.
Maar goed, het ging dus om cos(-arctan(3/4)).
Laten we zeggen dat
arctan(3/4) = α,
dan is
tan α = 3/4, met -½π < α < ½π
Nu maken we gebruik van de identiteit
1 + tan2α = sec2α,
waarvoor we uiteraard ook kunnen schrijven
1 + tan2α = 1/cos2α
We weten dat tan α = 3/4, dus hebben we
1/cos2α = 1 + (3/4)2 = 25/16,
en dus
cos2α = 16/25
Nu hebben we ook -½π < α < ½π en dus is cos α > 0, zodat we vinden
cos α = 4/5
De cosinusfunctie is een even functie, en dus is ook
cos(-α) = 4/5
En aangezien arctan(3/4) = α heb je dus:
cos(-arctan(3/4)) = cos(-α) = 4/5.
Voila.
Je zou ook een plaatje kunnen tekenen, en dan zie je dat je te maken hebt met een rechthoekige driehoek waarvan de zijden zich verhouden als 3 : 4 : 5 aangezien tan α = 3/4 gelijk is aan de overstaande rechthoekszijde gedeeld door de aanliggende rechthoekszijde van hoek α. En aangezien de cosinus van deze hoek gelijk is aan de aanliggende rechthoekszijde gedeeld door de schuine zijde, weet je dan direct dat cos α = 4/5.
[ Bericht 5% gewijzigd door Riparius op 26-06-2012 14:02:15 ]


Pagina 149 zegt [0, pi] en daar ligt -arctan(3/4) voor zover ik weet niet in. Als ik danwel 't boek iets fout heeft hoor ik het graag.
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt."Social order at the expense of liberty is hardly a bargain."


En ohja, sec ben ik nog niet tegengekomen in 't boek, maar de rest wel. Ik volg het verder, dank!
"Social order at the expense of liberty is hardly a bargain."


quote:Op dinsdag 26 juni 2012 12:35 schreef Quir het volgende:
Pagina 149 zegt [0, pi] en daar ligt -arctan(3/4) voor zover ik weet niet in. Als ik danwel 't boek iets fout heeft hoor ik het graag.Nee, je begrijpt het niet. Het pleit ook niet voor je dat je kennelijk meer vertrouwen hebt in een - foutief - gebruik van je rekenmachine dan in mijn uitleg. Ik vermoed dat je je rekenmachine op graden hebt laten staan in plaats van op radialen, en dan is het nogal wiedes dat de machine je invoer niet accepteert. Dit is weer typisch zo'n hersenloos gebruik van een calculator.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
Je hebt -½π < arctan(x) < ½π voor elke reële x, en arctan(0) = 0 en arctan(1) = ¼π. De arcus tangens functie is strict monotoon stijgend zodat arctan(0) < arctan(¾) < arctan(1) en dus 0 < arctan(¾) < ¼π en dus -¼π < -arctan(¾) < 0. En aangezien 0 < π < 4 is dus -1 < -¼π < 0 en daarmee -1 < -arctan(¾) < 0.
[ Bericht 14% gewijzigd door Riparius op 26-06-2012 14:56:31 ]


Ik had dus een paar uur geleden m'n wiskunde mondeling.
1. casus, wat eenvoudige goniometrie, raaklijnen en integralen. Op her en der een haakje en een k*2π na foutloos.
2. meetkunde: totaal verneukt (zoals iedereen)
3. wentelen, piece of cake.,
3. logaritmen. peanuts
4. optimaliseren, slordig begonnen, na een vermaning foutloos.
5. Mijn klok! Kreeg wat historische vragen(hij gaf toe dat mijn kennis van de wiskundige historie verder was dan de zijne)
6. Mercatorprojectie. Hij was onder de indruk, ondanks de geringe hoeveelheid tijd kreeg ik toch nog een vraag over poolcoördinaten. Mijn werkstuk is daarna ingenomen voor nadere observatie (hij wilde wel even kijken wat ik van deze 'hogere' wiskunde bakte.
Rip, bedankt!
1. casus, wat eenvoudige goniometrie, raaklijnen en integralen. Op her en der een haakje en een k*2π na foutloos.
2. meetkunde: totaal verneukt (zoals iedereen)
3. wentelen, piece of cake.,
3. logaritmen. peanuts
4. optimaliseren, slordig begonnen, na een vermaning foutloos.
5. Mijn klok! Kreeg wat historische vragen(hij gaf toe dat mijn kennis van de wiskundige historie verder was dan de zijne)
6. Mercatorprojectie. Hij was onder de indruk, ondanks de geringe hoeveelheid tijd kreeg ik toch nog een vraag over poolcoördinaten. Mijn werkstuk is daarna ingenomen voor nadere observatie (hij wilde wel even kijken wat ik van deze 'hogere' wiskunde bakte.
Rip, bedankt!


Graag gedaan. Maar wat hielden die meetkunde opgaven in?quote:Op dinsdag 26 juni 2012 14:50 schreef Amoeba het volgende:
Ik had dus een paar uur geleden m'n wiskunde mondeling.
1. casus, wat eenvoudige goniometrie, raaklijnen en integralen. Op her en der een haakje en een k*2π na foutloos.
2. meetkunde: totaal verneukt (zoals iedereen)
3. wentelen, piece of cake.,
3. logaritmen. peanuts
4. optimaliseren, slordig begonnen, na een vermaning foutloos.
5. Mijn klok! Kreeg wat historische vragen(hij gaf toe dat mijn kennis van de wiskundige historie verder was dan de zijne)
6. Mercatorprojectie. Hij was onder de indruk, ondanks de geringe hoeveelheid tijd kreeg ik toch nog een vraag over poolcoördinaten. Mijn werkstuk is daarna ingenomen voor nadere observatie (hij wilde wel even kijken wat ik van deze 'hogere' wiskunde bakte.
Rip, bedankt!


Helder!quote:Op dinsdag 26 juni 2012 12:41 schreef Riparius het volgende:
[..]
Nee, je begrijpt het niet. Het pleit ook niet voor je dat je kennelijk meer vertrouwen hebt in een - foutief - gebruik van je rekenmachine dan in mijn uitleg. Ik vermoed dat je je rekenmachine op graden hebt laten staan in plaats van op radialen, en dan is het nogal wiedes dat de machine je invoer niet accepteert. Dit is weer typisch zo'n hersenloos gebruik van een calculator.
Je hebt -½π < arctan(x) < ½π voor elke reële x, en arctan(0) = 0 en arctan(1) = ¼π. De arcus tangens functie is strict monotoon stijgend zodat arctan(0) < arctan(¾) < arctan(1) en dus 0 < arctan(¾) < ¼π en dus -¼π < -arctan(¾) < 0. En aangezien 0 < π < 4 is dus -1 < -¼π < 0 en daarmee -1 < -arctan(¾) < 0.
[ afbeelding ]
"Social order at the expense of liberty is hardly a bargain."


Oh, ik zie dat er in de tussentijd tekst is toegevoegd in de quote.
"Social order at the expense of liberty is hardly a bargain."


Je bent wel een botte zak af en toe, weet je. Ik heb het niet ingevoerd op mijn rekenmachine, ik had de uitkomst van de arctan gewoon verkeerd ingeschat. Ik leer, ik leer.
"Social order at the expense of liberty is hardly a bargain."


De omschreven cirkel, dat lukte nog. Ik zal straks even een schetsje maken. (oppervlakte van maantjes)


Je verwijst in je spoiler naar 't rekenmachien kennelijk in een poging om je gelijk te halen. Ik kon dus niets anders dan concluderen dat je had geprobeerd met je rekenmachine arccos(-arctan(3/4)) te bepalen en dat dat niet was gelukt omdat je machine een foutmelding gaf.quote:Op dinsdag 26 juni 2012 15:10 schreef Quir het volgende:
Je bent wel een botte zak af en toe, weet je. Ik heb het niet ingevoerd op mijn rekenmachine, ik had de uitkomst van de arctan gewoon verkeerd ingeschat. Ik leer, ik leer.
Maar als je het goed doet vind je (met de calculator van Windows) gewoon dat arccos(-arctan(3/4)) = 2,2698597989145314710273704204042 ...


Neen, ik wou m'n keuze voor 'het' in plaats van 'de' rechtvaardigen.
"Social order at the expense of liberty is hardly a bargain."


Wees blij dat die 'botte zak' je wil helpen.quote:Op dinsdag 26 juni 2012 15:10 schreef Quir het volgende:
Je bent wel een botte zak af en toe, weet je. Ik heb het niet ingevoerd op mijn rekenmachine, ik had de uitkomst van de arctan gewoon verkeerd ingeschat. Ik leer, ik leer.


Nou, zoals beloofd nog even die meetkunde opgave. Ik had een rechthoekige driehoek, met zijde a en b, de hypotenusa was dus 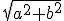
Goed, ik had de 2 omschreven cirkels van a en b al, dus met het middelpunt op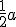 en
en 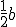
Het midden van beide zijdes was ook gemarkeerd, en dat was mijn eerste fout, ik ging daar zoeken. Ik moest het middelpunt van de omschreven cirkel aanwijzen. Nou, ik dus eerst beginnen met een faaltekening van de zwaartelijnen, en vervolgens kwam ik wel tot een goede constructie (met een kleine afwijking) door de middelloodlijnen te construeren. Pas toen hij zei het ligt op die zijde, maar WAAROM? ging ik met de stelling van Thales roepen. (Ja zo stom dat ik het niet eerder zag, ik kon me wel voor m'n kop slaan.) Maargoed, uiteindelijk kwam het er.
En ik had daar zoveel moeite mee, het liep niet, ik werd zenuwachtig, hij ging maar door. Hij kraste op de tekening (ik heb hem even geschetst) 2 stukjes in.
Nu moest ik aantonen dat de som van deze 2 stukjes gelijk was aan de oppervlakte van de driehoek. Toen vroeg hij me naar de oppervlakte van een cirkel, ik half verdwaasd zet er 2 pi * r neer, hij kijkt me aan, ik kijk nog eens, verander het r^2 maar liet de 2 staan. Echt, ik had het niet meer. Hij moest dus gewoon zeggen dat het pi r^2 was, maar dat terzijde.
Uiteindelijk had ik de formules van elke halve cirkel, maar ik kwam er niet tot, toen liet hij het maar zitten. Tot zover meetkunde, toen kwam het wentelen om de x-as en daar begon de pret. Ik zei ook maar gewoon eerlijk dat meetkunde een 4,8 was en me totaal niet lag, toen vroeg hij of e-machten me wel lagen, nou verder mocht hij losvragen wat hij wilde, alleen tijdens het optimaliseren ging ik eventjes mezelf voorbij en moest hij me tot rust manen vooraleer ik de opgave uit kon werken.
Ik had hem naderhand nog even gesproken over dat werkstuk, hij snapte het punt over de differentiaalvergelijking niet helemaal, hoe ik vanuit daar tot de integraal kwam. (De dy/dx en de integraal zijn toch 'inverse bewerkingen'?)
Maar verder wel voor al m'n examens dit jaar geslaagd (weet ik vrij zeker), Kreeg ik nog een of ander gesprek a.d.h.v. een ruzietje gisteren (nouja, 'ruzie', vechtpartij) met een jongen waarbij hij (en daarna ik) flink door het lint ging. Nu moet ik voor al m'n vrije uren (want daar schuilt mijn zwakte, ik kan daar niet goed mee omgaan als er geen opgave voor m'n neus ligt) een invulling zoeken met de stagebegeleider, dus bij Philips of ASML een stage lopen ofzo, anders kan ik het volgend jaar vergeten en bij de LOI beginnen. Leuk einde van het schooljaar.. Weet jij toevallig of je met 6 vwo wiskunde B en 4-5 vwo wiskunde D (ga ik volgend jaar dus afronden) daar iets te zoeken hebt?
[ Bericht 12% gewijzigd door #ANONIEM op 26-06-2012 19:06:20 ]
Goed, ik had de 2 omschreven cirkels van a en b al, dus met het middelpunt op
Het midden van beide zijdes was ook gemarkeerd, en dat was mijn eerste fout, ik ging daar zoeken. Ik moest het middelpunt van de omschreven cirkel aanwijzen. Nou, ik dus eerst beginnen met een faaltekening van de zwaartelijnen, en vervolgens kwam ik wel tot een goede constructie (met een kleine afwijking) door de middelloodlijnen te construeren. Pas toen hij zei het ligt op die zijde, maar WAAROM? ging ik met de stelling van Thales roepen. (Ja zo stom dat ik het niet eerder zag, ik kon me wel voor m'n kop slaan.) Maargoed, uiteindelijk kwam het er.
En ik had daar zoveel moeite mee, het liep niet, ik werd zenuwachtig, hij ging maar door. Hij kraste op de tekening (ik heb hem even geschetst) 2 stukjes in.
Nu moest ik aantonen dat de som van deze 2 stukjes gelijk was aan de oppervlakte van de driehoek. Toen vroeg hij me naar de oppervlakte van een cirkel, ik half verdwaasd zet er 2 pi * r neer, hij kijkt me aan, ik kijk nog eens, verander het r^2 maar liet de 2 staan. Echt, ik had het niet meer. Hij moest dus gewoon zeggen dat het pi r^2 was, maar dat terzijde.
Uiteindelijk had ik de formules van elke halve cirkel, maar ik kwam er niet tot, toen liet hij het maar zitten. Tot zover meetkunde, toen kwam het wentelen om de x-as en daar begon de pret. Ik zei ook maar gewoon eerlijk dat meetkunde een 4,8 was en me totaal niet lag, toen vroeg hij of e-machten me wel lagen, nou verder mocht hij losvragen wat hij wilde, alleen tijdens het optimaliseren ging ik eventjes mezelf voorbij en moest hij me tot rust manen vooraleer ik de opgave uit kon werken.
Ik had hem naderhand nog even gesproken over dat werkstuk, hij snapte het punt over de differentiaalvergelijking niet helemaal, hoe ik vanuit daar tot de integraal kwam. (De dy/dx en de integraal zijn toch 'inverse bewerkingen'?)
Maar verder wel voor al m'n examens dit jaar geslaagd (weet ik vrij zeker), Kreeg ik nog een of ander gesprek a.d.h.v. een ruzietje gisteren (nouja, 'ruzie', vechtpartij) met een jongen waarbij hij (en daarna ik) flink door het lint ging. Nu moet ik voor al m'n vrije uren (want daar schuilt mijn zwakte, ik kan daar niet goed mee omgaan als er geen opgave voor m'n neus ligt) een invulling zoeken met de stagebegeleider, dus bij Philips of ASML een stage lopen ofzo, anders kan ik het volgend jaar vergeten en bij de LOI beginnen. Leuk einde van het schooljaar.. Weet jij toevallig of je met 6 vwo wiskunde B en 4-5 vwo wiskunde D (ga ik volgend jaar dus afronden) daar iets te zoeken hebt?
[ Bericht 12% gewijzigd door #ANONIEM op 26-06-2012 19:06:20 ]


Wat bijzonder om een mondeling wiskunde-examen te hebben. Lijkt me veel rechtvaardiger, want je weet in een halve minuut of iemand bluft, terwijl je dat op papier van het beste moet uitgaan.
Oppervlakte van de hele figuur is
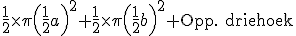
(halve cirkel op zijde a plus halve cirkel op zijde b plus driehoek)
Oppervlakte van de omgeschreven halve cirkel is
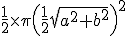
Eerste van tweede oppervlakte aftrekken en je houdt opp. driehoek over.
Oppervlakte van de hele figuur is
(halve cirkel op zijde a plus halve cirkel op zijde b plus driehoek)
Oppervlakte van de omgeschreven halve cirkel is
Eerste van tweede oppervlakte aftrekken en je houdt opp. driehoek over.


Je kunt met behulp van Pythagoras meteen (zonder rekenwerk) de conclusie trekken dat de oppervlakte van de gearceerde vlakdelen samen gelijk moet zijn aan de oppervlakte van de driehoek, zijnde ½ab. De beide halve cirkels op de rechthoekszijden hebben immers samen een oppervlakte die gelijk is aan de oppervlakte van de halve cirkel op de hypotenusa.quote:Op dinsdag 26 juni 2012 19:18 schreef twaalf het volgende:
Wat bijzonder om een mondeling wiskunde-examen te hebben. Lijkt me veel rechtvaardiger, want je weet in een halve minuut of iemand bluft, terwijl je dat op papier van het beste moet uitgaan.
Oppervlakte van de hele figuur is
(halve cirkel op zijde a plus halve cirkel op zijde b plus driehoek)
Oppervlakte van de omgeschreven halve cirkel is
Eerste van tweede oppervlakte aftrekken en je houdt opp. driehoek over.


Ik heb het ook absoluut niet op mondelinge tentamens. Er is ook geen enkele garantie op objectiviteit bij de beoordeling, en controle achteraf is niet mogelijk.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Is maar net bij wie je het afneemt. Soms kan je op een mondeling net een duwtje in de goede richting krijgen. Maar doe mij ook maar gewoon schriftelijkquote:Op dinsdag 26 juni 2012 20:36 schreef Amoeba het volgende:
Mondeling is veel lastiger dan schriftelijk. Je wordt echt opgejaagd soms.


het duwtje kan ook de andere kant op zijn, ik kreeg een keer 3 punten onder het gemiddelde van mijn andere vakkenquote:Op dinsdag 26 juni 2012 20:41 schreef thenxero het volgende:
[..]
Is maar net bij wie je het afneemt. Soms kan je op een mondeling net een duwtje in de goede richting krijgen. Maar doe mij ook maar gewoon schriftelijk
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Tsjah, wiskunde verliep eerlijk, scheikunde in mijn voordeel. Hij hield snel genoeg op met meetkunde en gaf me de kans om te knallen bij logaritmen. Ik kreeg alleen geen kans om aan die Mercatorprojectie te beginnen.


Ik zou er bloedzenuwachtig van worden. Als je iets niet snapt bij een schriftelijk examen kan je het even laten liggen en daarna verder gaan, maar zo'n opgave als die je net liet zien zou ik denk ik niks van bakken bij een mondelinge overhoring, en volgens mij niet veel vwo-leerlingen (je zei ook al dat iedereen het had verneukt, niet verwonderlijk).quote:Op dinsdag 26 juni 2012 20:36 schreef Amoeba het volgende:
Mondeling is veel lastiger dan schriftelijk. Je wordt echt opgejaagd soms.


Als ik die opgave hier nu had liggen en ik moest hem maken was me dat wel gelukt. Even rustig voor gaan zitten en gaan.
Maar je bént ook bloedzenuwachtig. Het mondeling examen telt net zo hard mee als het schriftelijk, dat maakt het een godverdomd belangrijk punt.
Ik krijg morgen te horen wat ik schriftelijk en mondeling gedaan heb, ofwel de uitslag.
Maar je bént ook bloedzenuwachtig. Het mondeling examen telt net zo hard mee als het schriftelijk, dat maakt het een godverdomd belangrijk punt.
Ik krijg morgen te horen wat ik schriftelijk en mondeling gedaan heb, ofwel de uitslag.


Nog een vraagje...
Als er staat... "Determine the area A of that portion of the paraboloid, x^2 + y^2 + z = 9, where x >= 0, y >= 0 and z >= 0."
Wordt er nu gevraagd naar de oppervlakte integraal?
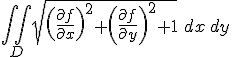
Als er staat... "Determine the area A of that portion of the paraboloid, x^2 + y^2 + z = 9, where x >= 0, y >= 0 and z >= 0."
Wordt er nu gevraagd naar de oppervlakte integraal?


Ik denk niet dat ze willen dat je een volume uitrekent, jij wel?quote:Op dinsdag 26 juni 2012 21:30 schreef Dale. het volgende:
Nog een vraagje...
Als er staat... "Determine the area A of that portion of the paraboloid, x^2 + y^2 + z = 9, where x >= 0, y >= 0 and z >= 0."
Wordt er nu gevraagd naar de oppervlakte integraal?
Begin dit maar eens goed door te nemen.quote:


Nee maar dat bereken je toch ook niet met een oppervlakte integraal? Je berekent daarmee het oppervlak van de vorm. Dus ja ik geloof dat ik gewoon correct zit. Ik zit er vooral over te duppen dat ik de vraagstelling niet snap, wat komt omdat ik op mijn aantekening een schets heb van de vorm waarbij ik het gebied dat op het x-y-vlak wordt geprojecteerd door de paraboloïde heb gearceerd en area heb bijgeschreven, mijn aantekening is vast goed bedoeld maar verkeerd opgeschrevenquote:Op woensdag 27 juni 2012 00:35 schreef Riparius het volgende:
[..]
Ik denk niet dat ze willen dat je een volume uitrekent, jij wel?
[..]
Begin dit maar eens goed door te nemen.


Gevraagd wordt de oppervlakte van een deel van de paraboloïde te berekenen. En je hebt daarvoor de juiste integraal. Maar nu moet je nog bepalen wat D voorstelt. Dat is inderdaad de projectie van het deel van de paraboloïde waarvan je de oppervlakte moet bepalen op het xy-vlak. Het is niet de bedoeling dat je de oppervlakte van D bepaalt, dat is een kwart van een cirkel met straal 3. Maar D is het gebied in het xy-vlak waarover je integreert.quote:Op woensdag 27 juni 2012 00:47 schreef Dale. het volgende:
[..]
Nee maar dat bereken je toch ook niet met een oppervlakte integraal? Je berekent daarmee het oppervlak van de vorm. Dus ja ik geloof dat ik gewoon correct zit. Ik zit er vooral over te dubben dat ik de vraagstelling niet snap, wat komt omdat ik op mijn aantekening een schets heb van de vorm waarbij ik het gebied dat op het x-y-vlak wordt geprojecteerd door de paraboloïde heb gearceerd en area heb bijgeschreven, mijn aantekening is vast goed bedoeld maar verkeerd opgeschreven


Thanks! Had D al bepaald, wist alleen niet of ik nu wel gewoon het juiste berekend heb. Je krijgt namelijk dan de integraal:quote:Op woensdag 27 juni 2012 01:09 schreef Riparius het volgende:
[..]
Gevraagd wordt de oppervlakte van een deel van de paraboloïde te berekenen. En je hebt daarvoor de juiste integraal. Maar nu moet je nog bepalen wat D voorstelt. Dat is inderdaad de projectie van het deel van de paraboloïde waarvan je de oppervlakte moet bepalen op het xy-vlak. Het is niet de bedoeling dat je de oppervlakte van D bepaalt, dat is een kwart van een cirkel met straal 3. Maar D is het gebied in het xy-vlak waarover je integreert.


Er komt zo te zien toch iets anders uit.quote:Op woensdag 27 juni 2012 01:27 schreef Dale. het volgende:
[..]
Thanks! Had D al bepaald, wist alleen niet of ik nu wel gewoon het juiste berekend heb. Je krijgt namelijk dan de integraal:
Je hebt kennelijk na de substitutie u = 1 + 4r2, du = 8rdr de verkeerde ondergrens voor je nieuwe variabele u gebruikt, namelijk 0 in plaats van 1. Substitutie geeft dit.
[ Bericht 5% gewijzigd door Riparius op 27-06-2012 01:59:48 ]


Ja klopt, was in dat laatste te snel, ondergrens niet vervangen.quote:Op woensdag 27 juni 2012 01:36 schreef Riparius het volgende:
[..]
Er komt zo te zien toch iets anders uit.
Je hebt kennelijk na de substitutie u = 1 + 4r2, du = 8rdr de verkeerde ondergrens voor je nieuwe variabele u gebruikt, namelijk 0 in plaats van 1. Substitutie geeft dit.


Je kunt eens beginnen met de site van Dick Klingens. Hier is heel veel te vinden over vlakke meetkunde, met bewijzen, en alles in het Nederlands (hetgeen van belang is omdat je dan ook vertrouwd raakt met de unieke Nederlandse termen voor veel meetkundige begrippen). Maar let op de waarschuwing (met een knipoog naar Plato): Μηδεὶς ἀγεωμέτρητος εἰσίτω μου τὴν στέγην (laat niemand die onkundig is in de meetkunde mijn site binnengaan).quote:


Net modellen en simulatie verneukt. Volgend jaar opnieuw doen, want ik ben op vakantie bij de hertentamens.
Ik zat bij het tentamen uren te kloten met een bepaalde opgave, uiteindelijk niet gelukt, probeer ik het thuis nog eens, lukt het allemaal in één keer.
Ik zat bij het tentamen uren te kloten met een bepaalde opgave, uiteindelijk niet gelukt, probeer ik het thuis nog eens, lukt het allemaal in één keer.


Aah jij ook al net in EDU bètaquote:Op woensdag 27 juni 2012 17:38 schreef kutkloon7 het volgende:
Net modellen en simulatie verneukt. Volgend jaar opnieuw doen, want ik ben op vakantie bij de hertentamens.
Ik zat bij het tentamen uren te kloten met een bepaalde opgave, uiteindelijk niet gelukt, probeer ik het thuis nog eens, lukt het allemaal in één keer.


Jaquote:Op woensdag 27 juni 2012 17:58 schreef thenxero het volgende:
[..]
Aah jij ook al net in EDU bèta. Hoe kan je het makkelijkste vak uit de bachelor nou verneuken man?
Ik had het dictaat niet bij me, en niet geleerd omdat ik nog een practicum moest maken. Die gast met wie ik dat doe mailde me twee dagen voor de deadline dat hij er toch niks van snapt, dus nu doe ik alles
En iedereen heeft het verpest, ik heb met de tentamens van afgelopen jaren geoefend en deze was echt veel lastiger. Er was eigenlijk maar één opgave die ik echt goed heb gedaan, die ging over de simplexmethode. Voor de rest was ik ook veel te zenuwachtig eigenlijk, thuis lukte het al een stuk beter toen ik er nog een keer naar keek.


Hoi,
Graag wil ik een vraag stellen over het volgende:
In Nederland gelden voor de netspanning (stopcontact) de volgende karakteristieken:
Vmax=325 V; T= 20 ms
Bereken de frequentie van de netspanning.
Nou had ik als antwoord: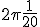 .
.
Daarbij had ik deze formule gebruikt: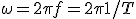
Maar volgens mij is mijn antwoord niet goed.. Mijn vraag is: wat moet ik in het begin doen en daarna om het goede antwoord te krijgen.
Graag wacht ik op uw reactie. Alvast bedankt voor uw antwoord.
Groet,
superky
Graag wil ik een vraag stellen over het volgende:
In Nederland gelden voor de netspanning (stopcontact) de volgende karakteristieken:
Vmax=325 V; T= 20 ms
Bereken de frequentie van de netspanning.
Nou had ik als antwoord:
Daarbij had ik deze formule gebruikt:
Maar volgens mij is mijn antwoord niet goed.. Mijn vraag is: wat moet ik in het begin doen en daarna om het goede antwoord te krijgen.
Graag wacht ik op uw reactie. Alvast bedankt voor uw antwoord.
Groet,
superky


Iedereen weet dat de frequentie van het lichtnet hier 50 Hz bedraagt, dus je antwoord is niet goed.quote:Op woensdag 27 juni 2012 18:41 schreef superky het volgende:
Hoi,
Graag wil ik een vraag stellen over het volgende:
In Nederland gelden voor de netspanning (stopcontact) de volgende karakteristieken:
Vmax=325 V; T= 20 ms
Bereken de frequentie van de netspanning.
Je hebt eenvoudig:
f = 1/T,
waarin f de frequentie is in Hz en T de periodeduur in seconden. En aangezien T = 20 ms = 0,02 sec. krijg je dus f = 1/0,02 Hz = 50 Hz.
[ Bericht 0% gewijzigd door Riparius op 28-06-2012 12:10:22 ]


Tja je moet ook wel het dictaat meenemenquote:Op woensdag 27 juni 2012 18:39 schreef kutkloon7 het volgende:
[..]
Ja
Ik had het dictaat niet bij me, en niet geleerd omdat ik nog een practicum moest maken. Die gast met wie ik dat doe mailde me twee dagen voor de deadline dat hij er toch niks van snapt, dus nu doe ik alles
En iedereen heeft het verpest, ik heb met de tentamens van afgelopen jaren geoefend en deze was echt veel lastiger. Er was eigenlijk maar één opgave die ik echt goed heb gedaan, die ging over de simplexmethode. Voor de rest was ik ook veel te zenuwachtig eigenlijk, thuis lukte het al een stuk beter toen ik er nog een keer naar keek.
Maarja dat was vorig jaar. Toen hadden ook alle 55 deelnemers het vak gehaald en was het gemiddelde een 8 (wel uniek


Ik voel me hier nu niet bepaald beter door, danku 
Het dictaat had ook niet veel geholpen trouwens, ik hoorde iedereen al klagen dat je er helemaal niks aan had.
Het dictaat had ook niet veel geholpen trouwens, ik hoorde iedereen al klagen dat je er helemaal niks aan had.


Tja, maar zonder dictaat had ik denk ik ook geen voldoende gehaald hoorquote:Op woensdag 27 juni 2012 18:54 schreef kutkloon7 het volgende:
Ik voel me hier nu niet bepaald beter door, danku
Het dictaat had ook niet veel geholpen trouwens, ik hoorde iedereen al klagen dat je er helemaal niks aan had.
Wel kut om het overnieuw te doen trouwens, kan je weer al die verslagen gaan maken.


Dankjewel!quote:Op woensdag 27 juni 2012 15:32 schreef Riparius het volgende:
[..]
Je kunt eens beginnen met de site van Dick Klingens. Hier is heel veel te vinden over vlakke meetkunde, met bewijzen, en alles in het Nederlands (hetgeen van belang is omdat je dan ook vertrouwd raakt met de unieke Nederlandse termen voor veel meetkundige begrippen). Maar let op de waarschuwing (met een knipoog naar Plato): Μηδεὶς ἀγεωμέτρητος εἰσίτω μου τὴν στέγην (laat niemand die onkundig is in de meetkunde mijn site binnengaan).
Mijn cijfer voor wiskunde B is bekend, slechts een 8..
Schriftelijk 7,8, mondeling 7,6...


Deed jij nou staatsexamen?quote:Op woensdag 27 juni 2012 20:22 schreef Amoeba het volgende:
[..]
Dankjewel!
Mijn cijfer voor wiskunde B is bekend, slechts een 8..
Schriftelijk 7,8, mondeling 7,6...
Hihi er staat sex


Om nog even terug te komen op die meetkunde opgave die je kreeg voorgeschoteld, dat was een klassieker, gebaseerd op propositie 31 uit het zesde boek van de elementen van Euclides (de examencommissie heeft dus ook niet veel fantasie). Kijk hier maar even.quote:


Beetje creatief zijn. We hebben:quote:Op woensdag 27 juni 2012 21:07 schreef Anoonumos het volgende:
Bepaal de laatste 2 cijfers van 123^456.
Hoe pak je zo'n soort opgave aan?
123 = 41∙3
en dus:
123456 = 41456∙3456
Hiermee heb je het probleem herleid tot het bepalen van de laatste twee cijfers van 41456 en van 3456, want als je die beide weet vind je door vermenigvuldiging de laatste twee cijfers van 123456.
Verder heb je
41456 = (40 + 1)456
Zie je wat je hiermee kunt doen?
Voor machten van 3 kun je bedenken dat 320 = 3486784401 zodat het patroon van de laatste twee cijfers zich dan weer gaat herhalen. Dus kan ik meteen zeggen dat de laatste twee cijfers van 3456 hetzelfde zijn als de laatste twee cijfers van 316 = 43046721. Nu mag je zelf weer even verder denken.


Niets mis mee, je mag daar best trots op zijn. De meetkundevraagjes zijn soms wat tricky en je moet er ook rekening mee houden dat je genaaid kan worden door de wijze van normeren, het is perfect mogelijk dat je volgens een correcte redenatie tot het juiste antwoord krijgt en dat je toch niet alle punten voor die vraag krijgt omdat de normering per vraag is opgedeeld in allerlei deelstappen, dat werkt nivellerend aangezien de zwakkere leerlingen al snel nog wat puntjes sprokkelen terwijl de goede leerlingen misschien wel stap b en c overslaan (niet expliciet opschrijven) en hierdoor wat punten mislopen. Indien de leraar zijn eigen oordeel zou mogen gebruiken in plaats van het normeringsmodel te gebruiken dan zou de standaarddeviatie waarschijnlijk wat groter zijn.quote:Mijn cijfer voor wiskunde B is bekend, slechts een 8..
Schriftelijk 7,8, mondeling 7,6...
Een 8 is voor mondeling bij veel examinatoren zo'n beetje het hoogst haalbare dus dat is ook in orde.
Als je jouw examen nog eens in zou gaan kijken laat je dan weten waar je de puntjes hebt laten liggen?
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL


Zou het niet makkelijker zijn om met modulorekenen te doen? Dan heb je niet zoveel inzicht nodig.quote:Op woensdag 27 juni 2012 21:54 schreef Riparius het volgende:
[..]
Beetje creatief zijn. We hebben:
123 = 41∙3
en dus:
123456 = 41456∙3456
Hiermee heb je het probleem herleid tot het bepalen van de laatste twee cijfers van 41456 en van 3456, want als je die beide weet vind je door vermenigvuldiging de laatste twee cijfers van 123456.
Verder heb je
41456 = (40 + 1)456
Zie je wat je hiermee kunt doen?
Voor machten van 3 kun je bedenken dat 320 = 3486784401 zodat het patroon van de laatste twee cijfers zich dan weer gaat herhalen. Dus kan ik meteen zeggen dat de laatste twee cijfers van 3456 hetzelfde zijn als de laatste twee cijfers van 316 = 43046721. Nu mag je zelf weer even verder denken.


Ik denk dat het juist omgekeerd is. Als je modulair kunt rekenen stel je waarschijnlijk niet zo'n vraag.quote:Op woensdag 27 juni 2012 22:53 schreef kutkloon7 het volgende:
[..]
Zou het niet makkelijker zijn om met modulorekenen te doen? Dan heb je niet zoveel inzicht nodig.


Dat is waar ja. Maar zo'n vraagstuk lijkt me een prima reden om het te leren, zo moeilijk is het nietquote:Op woensdag 27 juni 2012 22:57 schreef Riparius het volgende:
[..]
Ik denk dat het juist omgekeerd is. Als je kunt modulusrekenen stel je waarschijnlijk niet zo'n vraag.


Hier staat wel goede uitleg voor dat soort problemen, met wat sommen (die trouwens erg veel op die vraag lijken).quote:Op woensdag 27 juni 2012 21:07 schreef Anoonumos het volgende:
Bepaal de laatste 2 cijfers van 123^456.
Hoe pak je zo'n soort opgave aan?


Ik krijg mijn examen niet meer te zien, maar ik kan het wel vertellen. De stappen van P passeert de evenwichtsstand op t=7,5 enzo, ik vulde direct die t waarde in. De meetkunde opgaven kreeg ik niet af en 2 vragen stuurden me het bos in (deels goed, dat wel).quote:Op woensdag 27 juni 2012 22:30 schreef Bram_van_Loon het volgende:
[..]
Niets mis mee, je mag daar best trots op zijn. De meetkundevraagjes zijn soms wat tricky en je moet er ook rekening mee houden dat je genaaid kan worden door de wijze van normeren, het is perfect mogelijk dat je volgens een correcte redenatie tot het juiste antwoord krijgt en dat je toch niet alle punten voor die vraag krijgt omdat de normering per vraag is opgedeeld in allerlei deelstappen, dat werkt nivellerend aangezien de zwakkere leerlingen al snel nog wat puntjes sprokkelen terwijl de goede leerlingen misschien wel stap b en c overslaan (niet expliciet opschrijven) en hierdoor wat punten mislopen. Indien de leraar zijn eigen oordeel zou mogen gebruiken in plaats van het normeringsmodel te gebruiken dan zou de standaarddeviatie waarschijnlijk wat groter zijn.
Een 8 is voor mondeling bij veel examinatoren zo'n beetje het hoogst haalbare dus dat is ook in orde.
Als je jouw examen nog eens in zou gaan kijken laat je dan weten waar je de puntjes hebt laten liggen?


Dat klopt, alleen moet je dan nog wel wat handige keuzes zien te maken, waarbij een (simpele) calculator nu eindelijk eens wél van pas komt.quote:Op woensdag 27 juni 2012 23:03 schreef kutkloon7 het volgende:
[..]
Dat is waar ja. Maar zo'n vraagstuk lijkt me een prima reden om het te leren, zo moeilijk is het niet
Omdat het er niet naar uit ziet dat Anoonumos nog reageert zal ik mijn aanpak even verder uitwerken voor eventuele andere geïnteresseerden. We hadden
41456 = (40 + 1)456
Nu bevatten alle termen van dit binomium uitgezonderd de laatste twee tenminste twee factoren 40, wat dus betekent dat alle termen, uitgezonderd de laatste twee, veelvouden zijn van 100 en daarmee geen bijdrage leveren aan de laatste twee cijfers van 41456. We kunnen dus volstaan met het optellen van de laatste twee termen van het binomium. We hebben dan
41456 = (40 + 1)456 = ... + 456∙401∙1455 + 1∙400∙1456 = ... + 456∙40 + 1 = ... + 18241, zodat de laatste twee cijfers dus 41 zijn.
We hadden al de laatste twee cijfers van 3456, namelijk 21, en het product van 41 en 21 is 861 zodat de laatste twee cijfers van 123456 = 41456∙3456 dus ook 61 zijn.
Met modulair rekenen bedenk je dat 123 ≡ 23 (mod 100). Het is nu zaak eerst een macht van 23 te vinden waarvan het getal gevormd door de twee eindcijfers liefst zo klein mogelijk is. Met een eenvoudige calculator waarmee je gemakkelijk herhaalde vermenigvuldigingen kunt uitvoeren (ik heb de rekenmachine van Windows gebruikt) vind je dan bijvoorbeeld dat
2315 = 266635235464391245607
zodat
123456 ≡ 23456 = (2315)30∙236 ≡ 730∙236 ≡ 49∙89 = 4361 ≡ 61 (mod 100),
en dat klopt uiteraard met wat we eerder vonden.
Als je een calculator gebruikt die niet genoeg significante cijfers heeft om 2315 of 730 = 22539340290692258087863249 te berekenen, dan gebruik je dat 74 = 2401, zodat
730 = (74)7∙72 ≡ 17∙49 = 49 (mod 100).
Evenzo kun je gebruik maken van 235 = 6436343 zodat
2315 = (235)3 ≡ 433 = 79507 ≡ 7 (mod 100),
en trouwens ook
2320 = (235)4 ≡ 434 = 3418801 ≡ 1 (mod 100).
Een alternatieve berekening met een calculator die alleen 'kleine' getallen aankan, of met pen en papier, wordt dan:
123456 ≡ 23456 = (2320)22∙2315∙23 ≡ 1∙7∙23 = 161 ≡ 61 (mod 100).
[ Bericht 0% gewijzigd door Riparius op 28-06-2012 13:48:25 ]


123 = -1 mod 4 dus 123456 = 1 mod 4.
123 = -2 mod 25 dus 123456 = (-2)456 = 2456 mod 25
Je kan de machten van 2 modulo 25 makkelijk uitrekenen: 2, 4, 8, 16, 7, 14, 3, 6, 12, 24, 23, 21, 17, 9, 18, 11, 22, 19, 13, 1. Zo vinden we een periode van 20 (met wat meer kennis over modulorekenen is overigens direct in te zien dat 220=1 mod 25 geldt, maar dat terzijde).
Dus 2456 = 216 mod 25 = 11 mod 25 zoals we uit het rijtje kunnen afleiden.
De getallen modulo 100 die 11 mod 25 zijn, zijn 11, 36, 61, 86. Alleen 61 daarvan is 1 mod 4.
Daar zijn toch geen ingewikkelde rekenpartijen voor nodig.
123 = -2 mod 25 dus 123456 = (-2)456 = 2456 mod 25
Je kan de machten van 2 modulo 25 makkelijk uitrekenen: 2, 4, 8, 16, 7, 14, 3, 6, 12, 24, 23, 21, 17, 9, 18, 11, 22, 19, 13, 1. Zo vinden we een periode van 20 (met wat meer kennis over modulorekenen is overigens direct in te zien dat 220=1 mod 25 geldt, maar dat terzijde).
Dus 2456 = 216 mod 25 = 11 mod 25 zoals we uit het rijtje kunnen afleiden.
De getallen modulo 100 die 11 mod 25 zijn, zijn 11, 36, 61, 86. Alleen 61 daarvan is 1 mod 4.
Daar zijn toch geen ingewikkelde rekenpartijen voor nodig.


Dat is inderdaad heel elegant, ik had er niet aan gedacht om eerst het getal mod 4 en mod 25 te bepalen. Maar ik doe dit soort dingen zelden.quote:Op donderdag 28 juni 2012 14:16 schreef thabit het volgende:
123 = -1 mod 4 dus 123456 = 1 mod 4.
123 = -2 mod 25 dus 123456 = (-2)456 = 2456 mod 25
Je kan de machten van 2 modulo 25 makkelijk uitrekenen: 2, 4, 8, 16, 7, 14, 3, 6, 12, 24, 23, 21, 17, 9, 18, 11, 22, 19, 13, 1. Zo vinden we een periode van 20 (met wat meer kennis over modulorekenen is overigens direct in te zien dat 220=1 mod 25 geldt, maar dat terzijde).
Dus 2456 = 216 mod 25 = 11 mod 25 zoals we uit het rijtje kunnen afleiden.
De getallen modulo 100 die 11 mod 25 zijn, zijn 11, 36, 61, 86. Alleen 61 daarvan is 1 mod 4.
Daar zijn toch geen ingewikkelde rekenpartijen voor nodig.
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |





