[Bèta wiskunde] Huiswerk- en vragentopic

dinsdag 26 juni 2012 @ 15:08:08 #51

Quir

quote:
Op dinsdag 26 juni 2012 12:41 schreef Riparius het volgende:

[..]

Nee, je begrijpt het niet. Het pleit ook niet voor je dat je kennelijk meer vertrouwen hebt in een - foutief - gebruik van je rekenmachine dan in mijn uitleg. Ik vermoed dat je je rekenmachine op graden hebt laten staan in plaats van op radialen, en dan is het nogal wiedes dat de machine je invoer niet accepteert. Dit is weer typisch zo'n hersenloos gebruik van een calculator.

Je hebt -½π < arctan(x) < ½π voor elke reële x, en arctan(0) = 0 en arctan(1) = ¼π. De arcus tangens functie is strict monotoon stijgend zodat arctan(0) < arctan(¾) < arctan(1) en dus 0 < arctan(¾) < ¼π en dus -¼π < -arctan(¾) < 0. En aangezien 0 < π < 4 is dus -1 < -¼π < 0 en daarmee -1 < -arctan(¾) < 0.

[ afbeelding ]

Helder!

"Social order at the expense of liberty is hardly a bargain."

dinsdag 26 juni 2012 @ 15:09:17 #52

Quir

Oh, ik zie dat er in de tussentijd tekst is toegevoegd in de quote.

"Social order at the expense of liberty is hardly a bargain."

dinsdag 26 juni 2012 @ 15:10:19 #53

Quir

Je bent wel een botte zak af en toe, weet je. Ik heb het niet ingevoerd op mijn rekenmachine, ik had de uitkomst van de arctan gewoon verkeerd ingeschat. Ik leer, ik leer.

"Social order at the expense of liberty is hardly a bargain."

dinsdag 26 juni 2012 @ 15:25:56 #54

#ANONIEM

De omschreven cirkel, dat lukte nog. Ik zal straks even een schetsje maken. (oppervlakte van maantjes)

dinsdag 26 juni 2012 @ 15:27:26 #55

Riparius

quote:
Op dinsdag 26 juni 2012 15:10 schreef Quir het volgende:
Je bent wel een botte zak af en toe, weet je. Ik heb het niet ingevoerd op mijn rekenmachine, ik had de uitkomst van de arctan gewoon verkeerd ingeschat. Ik leer, ik leer.

Je verwijst in je spoiler naar 't rekenmachien kennelijk in een poging om je gelijk te halen. Ik kon dus niets anders dan concluderen dat je had geprobeerd met je rekenmachine arccos(-arctan(3/4)) te bepalen en dat dat niet was gelukt omdat je machine een foutmelding gaf.

Maar als je het goed doet vind je (met de calculator van Windows) gewoon dat arccos(-arctan(3/4)) = 2,2698597989145314710273704204042 ...

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

dinsdag 26 juni 2012 @ 15:33:32 #56

Quir

Neen, ik wou m'n keuze voor 'het' in plaats van 'de' rechtvaardigen.

"Social order at the expense of liberty is hardly a bargain."

dinsdag 26 juni 2012 @ 15:41:34 #57

#ANONIEM

quote:
Op dinsdag 26 juni 2012 15:10 schreef Quir het volgende:
Je bent wel een botte zak af en toe, weet je. Ik heb het niet ingevoerd op mijn rekenmachine, ik had de uitkomst van de arctan gewoon verkeerd ingeschat. Ik leer, ik leer.

Wees blij dat die 'botte zak' je wil helpen.

dinsdag 26 juni 2012 @ 15:54:11 #58

Quir

En dat ben ik.

"Social order at the expense of liberty is hardly a bargain."

dinsdag 26 juni 2012 @ 19:01:44 #59

#ANONIEM

Nou, zoals beloofd nog even die meetkunde opgave. Ik had een rechthoekige driehoek, met zijde a en b, de hypotenusa was dus 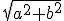$\sqrt{a^2+b^2}$

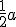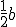
Goed, ik had de 2 omschreven cirkels van a en b al, dus met het middelpunt op $\frac{1}{2}a$ en $\frac{1}{2}b$

Het midden van beide zijdes was ook gemarkeerd, en dat was mijn eerste fout, ik ging daar zoeken. Ik moest het middelpunt van de omschreven cirkel aanwijzen. Nou, ik dus eerst beginnen met een faaltekening van de zwaartelijnen, en vervolgens kwam ik wel tot een goede constructie (met een kleine afwijking) door de middelloodlijnen te construeren. Pas toen hij zei het ligt op die zijde, maar WAAROM? ging ik met de stelling van Thales roepen. (Ja zo stom dat ik het niet eerder zag, ik kon me wel voor m'n kop slaan.) Maargoed, uiteindelijk kwam het er.

En ik had daar zoveel moeite mee, het liep niet, ik werd zenuwachtig, hij ging maar door. Hij kraste op de tekening (ik heb hem even geschetst) 2 stukjes in.

Nu moest ik aantonen dat de som van deze 2 stukjes gelijk was aan de oppervlakte van de driehoek. Toen vroeg hij me naar de oppervlakte van een cirkel, ik half verdwaasd zet er 2 pi * r neer, hij kijkt me aan, ik kijk nog eens, verander het r^2 maar liet de 2 staan. Echt, ik had het niet meer. Hij moest dus gewoon zeggen dat het pi r^2 was, maar dat terzijde.

Uiteindelijk had ik de formules van elke halve cirkel, maar ik kwam er niet tot, toen liet hij het maar zitten. Tot zover meetkunde, toen kwam het wentelen om de x-as en daar begon de pret. Ik zei ook maar gewoon eerlijk dat meetkunde een 4,8 was en me totaal niet lag, toen vroeg hij of e-machten me wel lagen, nou verder mocht hij losvragen wat hij wilde, alleen tijdens het optimaliseren ging ik eventjes mezelf voorbij en moest hij me tot rust manen vooraleer ik de opgave uit kon werken.

Ik had hem naderhand nog even gesproken over dat werkstuk, hij snapte het punt over de differentiaalvergelijking niet helemaal, hoe ik vanuit daar tot de integraal kwam. (De dy/dx en de integraal zijn toch 'inverse bewerkingen'?)

Maar verder wel voor al m'n examens dit jaar geslaagd (weet ik vrij zeker), Kreeg ik nog een of ander gesprek a.d.h.v. een ruzietje gisteren (nouja, 'ruzie', vechtpartij) met een jongen waarbij hij (en daarna ik) flink door het lint ging. Nu moet ik voor al m'n vrije uren (want daar schuilt mijn zwakte, ik kan daar niet goed mee omgaan als er geen opgave voor m'n neus ligt) een invulling zoeken met de stagebegeleider, dus bij Philips of ASML een stage lopen ofzo, anders kan ik het volgend jaar vergeten en bij de LOI beginnen. Leuk einde van het schooljaar.. Weet jij toevallig of je met 6 vwo wiskunde B en 4-5 vwo wiskunde D (ga ik volgend jaar dus afronden) daar iets te zoeken hebt?

[ Bericht 12% gewijzigd door #ANONIEM op 26-06-2012 19:06:20 ]

dinsdag 26 juni 2012 @ 19:06:57 #60

#ANONIEM

echt ik wil bijles in meetkunde ofzo

dinsdag 26 juni 2012 @ 19:18:42 #61

twaalf

Wat bijzonder om een mondeling wiskunde-examen te hebben. Lijkt me veel rechtvaardiger, want je weet in een halve minuut of iemand bluft, terwijl je dat op papier van het beste moet uitgaan.

Oppervlakte van de hele figuur is
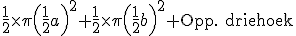
$\frac{1}{2}\times \pi \left(\frac{1}{2}a\right)^2+\frac{1}{2}\times \pi \left(\frac{1}{2}b\right)^2+\textrm{Opp. driehoek}$
(halve cirkel op zijde a plus halve cirkel op zijde b plus driehoek)
Oppervlakte van de omgeschreven halve cirkel is
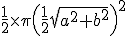
$\frac{1}{2}\times \pi \left(\frac{1}{2}\sqrt{a^2+b^2}\right)^2$
Eerste van tweede oppervlakte aftrekken en je houdt opp. driehoek over.

dinsdag 26 juni 2012 @ 19:37:03 #62

#ANONIEM

Ik zag dat toen echt niet. Maargoed, als je de 10 niet verdient hoor je hem ook niet te krijgen.

dinsdag 26 juni 2012 @ 19:51:31 #63

Riparius

quote:
Op dinsdag 26 juni 2012 19:18 schreef twaalf het volgende:
Wat bijzonder om een mondeling wiskunde-examen te hebben. Lijkt me veel rechtvaardiger, want je weet in een halve minuut of iemand bluft, terwijl je dat op papier van het beste moet uitgaan.

Oppervlakte van de hele figuur is
$\frac{1}{2}\times \pi \left(\frac{1}{2}a\right)^2+\frac{1}{2}\times \pi \left(\frac{1}{2}b\right)^2+\textrm{Opp. driehoek}$
(halve cirkel op zijde a plus halve cirkel op zijde b plus driehoek)
Oppervlakte van de omgeschreven halve cirkel is
$\frac{1}{2}\times \pi \left(\frac{1}{2}\sqrt{a^2+b^2}\right)^2$
Eerste van tweede oppervlakte aftrekken en je houdt opp. driehoek over.

Je kunt met behulp van Pythagoras meteen (zonder rekenwerk) de conclusie trekken dat de oppervlakte van de gearceerde vlakdelen samen gelijk moet zijn aan de oppervlakte van de driehoek, zijnde ½ab. De beide halve cirkels op de rechthoekszijden hebben immers samen een oppervlakte die gelijk is aan de oppervlakte van de halve cirkel op de hypotenusa.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

dinsdag 26 juni 2012 @ 20:36:10 #64

#ANONIEM

Mondeling is veel lastiger dan schriftelijk. Je wordt echt opgejaagd soms.

dinsdag 26 juni 2012 @ 20:38:52 #65

GlowMouse

l'état, c'est moi

Ik heb het ook absoluut niet op mondelinge tentamens. Er is ook geen enkele garantie op objectiviteit bij de beoordeling, en controle achteraf is niet mogelijk.

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

dinsdag 26 juni 2012 @ 20:41:40 #66

thenxero

quote:
Op dinsdag 26 juni 2012 20:36 schreef Amoeba het volgende:
Mondeling is veel lastiger dan schriftelijk. Je wordt echt opgejaagd soms.

Is maar net bij wie je het afneemt. Soms kan je op een mondeling net een duwtje in de goede richting krijgen. Maar doe mij ook maar gewoon schriftelijk

dinsdag 26 juni 2012 @ 20:44:01 #67

GlowMouse

l'état, c'est moi

quote:
Op dinsdag 26 juni 2012 20:41 schreef thenxero het volgende:

[..]

Is maar net bij wie je het afneemt. Soms kan je op een mondeling net een duwtje in de goede richting krijgen. Maar doe mij ook maar gewoon schriftelijk

het duwtje kan ook de andere kant op zijn, ik kreeg een keer 3 punten onder het gemiddelde van mijn andere vakken

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

dinsdag 26 juni 2012 @ 20:55:16 #68

#ANONIEM

Tsjah, wiskunde verliep eerlijk, scheikunde in mijn voordeel. Hij hield snel genoeg op met meetkunde en gaf me de kans om te knallen bij logaritmen. Ik kreeg alleen geen kans om aan die Mercatorprojectie te beginnen.

dinsdag 26 juni 2012 @ 21:24:35 #69

kutkloon7

quote:
Op dinsdag 26 juni 2012 20:36 schreef Amoeba het volgende:
Mondeling is veel lastiger dan schriftelijk. Je wordt echt opgejaagd soms.

Ik zou er bloedzenuwachtig van worden. Als je iets niet snapt bij een schriftelijk examen kan je het even laten liggen en daarna verder gaan, maar zo'n opgave als die je net liet zien zou ik denk ik niks van bakken bij een mondelinge overhoring, en volgens mij niet veel vwo-leerlingen (je zei ook al dat iedereen het had verneukt, niet verwonderlijk).

dinsdag 26 juni 2012 @ 21:26:08 #70

#ANONIEM

Als ik die opgave hier nu had liggen en ik moest hem maken was me dat wel gelukt. Even rustig voor gaan zitten en gaan.

Maar je bént ook bloedzenuwachtig. Het mondeling examen telt net zo hard mee als het schriftelijk, dat maakt het een godverdomd belangrijk punt.

Ik krijg morgen te horen wat ik schriftelijk en mondeling gedaan heb, ofwel de uitslag.

dinsdag 26 juni 2012 @ 21:30:13 #71

Dale.

Nog een vraagje...

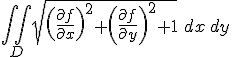
Als er staat... "Determine the area A of that portion of the paraboloid, x^2 + y^2 + z = 9, where x >= 0, y >= 0 and z >= 0."

Wordt er nu gevraagd naar de oppervlakte integraal?

$\iint_D \sqrt{\left({\partial f \over \partial x}\right)^2+\left({\partial f \over \partial y}\right)^2+1}\, \, dx\, dy$

woensdag 27 juni 2012 @ 00:35:57 #72

Riparius

quote:
Op dinsdag 26 juni 2012 21:30 schreef Dale. het volgende:
Nog een vraagje...

Als er staat... "Determine the area A of that portion of the paraboloid, x^2 + y^2 + z = 9, where x >= 0, y >= 0 and z >= 0."

Wordt er nu gevraagd naar de oppervlakte integraal?

Ik denk niet dat ze willen dat je een volume uitrekent, jij wel?

quote:
$\iint_D \sqrt{\left({\partial f \over \partial x}\right)^2+\left({\partial f \over \partial y}\right)^2+1}\, \, dx\, dy$

Begin dit maar eens goed door te nemen.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

woensdag 27 juni 2012 @ 00:47:27 #73

Dale.

quote:
Op woensdag 27 juni 2012 00:35 schreef Riparius het volgende:

[..]

Ik denk niet dat ze willen dat je een volume uitrekent, jij wel?

[..]

Begin dit maar eens goed door te nemen.

Nee maar dat bereken je toch ook niet met een oppervlakte integraal? Je berekent daarmee het oppervlak van de vorm. Dus ja ik geloof dat ik gewoon correct zit. Ik zit er vooral over te duppen dat ik de vraagstelling niet snap, wat komt omdat ik op mijn aantekening een schets heb van de vorm waarbij ik het gebied dat op het x-y-vlak wordt geprojecteerd door de paraboloïde heb gearceerd en area heb bijgeschreven, mijn aantekening is vast goed bedoeld maar verkeerd opgeschreven

woensdag 27 juni 2012 @ 01:09:35 #74

Riparius

quote:
Op woensdag 27 juni 2012 00:47 schreef Dale. het volgende:

[..]

Nee maar dat bereken je toch ook niet met een oppervlakte integraal? Je berekent daarmee het oppervlak van de vorm. Dus ja ik geloof dat ik gewoon correct zit. Ik zit er vooral over te dubben dat ik de vraagstelling niet snap, wat komt omdat ik op mijn aantekening een schets heb van de vorm waarbij ik het gebied dat op het x-y-vlak wordt geprojecteerd door de paraboloïde heb gearceerd en area heb bijgeschreven, mijn aantekening is vast goed bedoeld maar verkeerd opgeschreven

Gevraagd wordt de oppervlakte van een deel van de paraboloïde te berekenen. En je hebt daarvoor de juiste integraal. Maar nu moet je nog bepalen wat D voorstelt. Dat is inderdaad de projectie van het deel van de paraboloïde waarvan je de oppervlakte moet bepalen op het xy-vlak. Het is niet de bedoeling dat je de oppervlakte van D bepaalt, dat is een kwart van een cirkel met straal 3. Maar D is het gebied in het xy-vlak waarover je integreert.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

woensdag 27 juni 2012 @ 01:27:09 #75

Dale.

quote:
Op woensdag 27 juni 2012 01:09 schreef Riparius het volgende:

[..]

Gevraagd wordt de oppervlakte van een deel van de paraboloïde te berekenen. En je hebt daarvoor de juiste integraal. Maar nu moet je nog bepalen wat D voorstelt. Dat is inderdaad de projectie van het deel van de paraboloïde waarvan je de oppervlakte moet bepalen op het xy-vlak. Het is niet de bedoeling dat je de oppervlakte van D bepaalt, dat is een kwart van een cirkel met straal 3. Maar D is het gebied in het xy-vlak waarover je integreert.

Thanks! Had D al bepaald, wist alleen niet of ik nu wel gewoon het juiste berekend heb. Je krijgt namelijk dan de integraal: $\int_0^{pi/2}\int_0^3 \sqrt{1 + 4r^2}rdrd\theta = \frac{37}{24}\sqrt{37}\pi$

woensdag 27 juni 2012 @ 01:36:17 #76

Riparius

quote:
Op woensdag 27 juni 2012 01:27 schreef Dale. het volgende:

[..]

Thanks! Had D al bepaald, wist alleen niet of ik nu wel gewoon het juiste berekend heb. Je krijgt namelijk dan de integraal: $\int_0^{pi/2}\int_0^3 \sqrt{1 + 4r^2}rdrd\theta = \frac{37}{24}\sqrt{37}\pi$

Er komt zo te zien toch iets anders uit.

Je hebt kennelijk na de substitutie u = 1 + 4r², du = 8rdr de verkeerde ondergrens voor je nieuwe variabele u gebruikt, namelijk 0 in plaats van 1. Substitutie geeft dit.

[ Bericht 5% gewijzigd door Riparius op 27-06-2012 01:59:48 ]

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

woensdag 27 juni 2012 @ 12:09:11 #77

Dale.

quote:
Op woensdag 27 juni 2012 01:36 schreef Riparius het volgende:

[..]

Er komt zo te zien toch iets anders uit.

Je hebt kennelijk na de substitutie u = 1 + 4r², du = 8rdr de verkeerde ondergrens voor je nieuwe variabele u gebruikt, namelijk 0 in plaats van 1. Substitutie geeft dit.

Ja klopt, was in dat laatste te snel, ondergrens niet vervangen.

woensdag 27 juni 2012 @ 15:32:07 #78

Riparius

quote:
Op dinsdag 26 juni 2012 19:06 schreef Amoeba het volgende:
echt ik wil bijles in meetkunde ofzo

Je kunt eens beginnen met de site van Dick Klingens. Hier is heel veel te vinden over vlakke meetkunde, met bewijzen, en alles in het Nederlands (hetgeen van belang is omdat je dan ook vertrouwd raakt met de unieke Nederlandse termen voor veel meetkundige begrippen). Maar let op de waarschuwing (met een knipoog naar Plato): Μηδεὶς ἀγεωμέτρητος εἰσίτω μου τὴν στέγην (laat niemand die onkundig is in de meetkunde mijn site binnengaan).

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

woensdag 27 juni 2012 @ 17:38:44 #79

kutkloon7

Net modellen en simulatie verneukt. Volgend jaar opnieuw doen, want ik ben op vakantie bij de hertentamens.
Ik zat bij het tentamen uren te kloten met een bepaalde opgave, uiteindelijk niet gelukt, probeer ik het thuis nog eens, lukt het allemaal in één keer.

woensdag 27 juni 2012 @ 17:58:35 #80

thenxero

quote:
Op woensdag 27 juni 2012 17:38 schreef kutkloon7 het volgende:
Net modellen en simulatie verneukt. Volgend jaar opnieuw doen, want ik ben op vakantie bij de hertentamens.
Ik zat bij het tentamen uren te kloten met een bepaalde opgave, uiteindelijk niet gelukt, probeer ik het thuis nog eens, lukt het allemaal in één keer.

Aah jij ook al net in EDU bèta

. Hoe kan je het makkelijkste vak uit de bachelor nou verneuken man?

woensdag 27 juni 2012 @ 18:39:53 #81

kutkloon7

quote:
Op woensdag 27 juni 2012 17:58 schreef thenxero het volgende:

[..]

Aah jij ook al net in EDU bèta . Hoe kan je het makkelijkste vak uit de bachelor nou verneuken man?

Ik had het dictaat niet bij me, en niet geleerd omdat ik nog een practicum moest maken. Die gast met wie ik dat doe mailde me twee dagen voor de deadline dat hij er toch niks van snapt, dus nu doe ik alles

En iedereen heeft het verpest, ik heb met de tentamens van afgelopen jaren geoefend en deze was echt veel lastiger. Er was eigenlijk maar één opgave die ik echt goed heb gedaan, die ging over de simplexmethode. Voor de rest was ik ook veel te zenuwachtig eigenlijk, thuis lukte het al een stuk beter toen ik er nog een keer naar keek.

woensdag 27 juni 2012 @ 18:41:37 #82

superky

Hoi,

Graag wil ik een vraag stellen over het volgende:

In Nederland gelden voor de netspanning (stopcontact) de volgende karakteristieken:

Vmax=325 V; T= 20 ms

Bereken de frequentie van de netspanning.

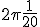Nou had ik als antwoord: $2 \pi \frac{1}{20}$ .
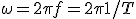
Daarbij had ik deze formule gebruikt: $\omega=2 \pi f=2\pi1/T$

Maar volgens mij is mijn antwoord niet goed.. Mijn vraag is: wat moet ik in het begin doen en daarna om het goede antwoord te krijgen.

Graag wacht ik op uw reactie. Alvast bedankt voor uw antwoord.

Groet,

superky

woensdag 27 juni 2012 @ 18:45:01 #83

Riparius

quote:
Op woensdag 27 juni 2012 18:41 schreef superky het volgende:
Hoi,

Graag wil ik een vraag stellen over het volgende:

In Nederland gelden voor de netspanning (stopcontact) de volgende karakteristieken:

Vmax=325 V; T= 20 ms

Bereken de frequentie van de netspanning.

Iedereen weet dat de frequentie van het lichtnet hier 50 Hz bedraagt, dus je antwoord is niet goed.

Je hebt eenvoudig:

f = 1/T,

waarin f de frequentie is in Hz en T de periodeduur in seconden. En aangezien T = 20 ms = 0,02 sec. krijg je dus f = 1/0,02 Hz = 50 Hz.

[ Bericht 0% gewijzigd door Riparius op 28-06-2012 12:10:22 ]

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

woensdag 27 juni 2012 @ 18:49:47 #84

thenxero

quote:
Op woensdag 27 juni 2012 18:39 schreef kutkloon7 het volgende:

[..]

Ja
Ik had het dictaat niet bij me, en niet geleerd omdat ik nog een practicum moest maken. Die gast met wie ik dat doe mailde me twee dagen voor de deadline dat hij er toch niks van snapt, dus nu doe ik alles

En iedereen heeft het verpest, ik heb met de tentamens van afgelopen jaren geoefend en deze was echt veel lastiger. Er was eigenlijk maar één opgave die ik echt goed heb gedaan, die ging over de simplexmethode. Voor de rest was ik ook veel te zenuwachtig eigenlijk, thuis lukte het al een stuk beter toen ik er nog een keer naar keek.

Tja je moet ook wel het dictaat meenemen

. Toen ik dat vak deed ben ik naar precies 0 hoorcolleges en werkcolleges geweest omdat ik ook een boeiender tweedejaars vak volgde tegelijkertijd. Ik had geen enkele werkcollegeopgave gemaakt. Alleen de verslagen gemaakt en de stellingen in het dictaat doorgelezen. Simplex methode had ik overgeslagen omdat het veel leeswerk was en best vaag uitgelegd. Toch dat vak afgesloten met een 8.5

.

Maarja dat was vorig jaar. Toen hadden ook alle 55 deelnemers het vak gehaald en was het gemiddelde een 8 (wel uniek

) .

woensdag 27 juni 2012 @ 18:54:18 #85

kutkloon7

Ik voel me hier nu niet bepaald beter door, danku

Het dictaat had ook niet veel geholpen trouwens, ik hoorde iedereen al klagen dat je er helemaal niks aan had.

woensdag 27 juni 2012 @ 18:58:20 #86

thenxero

quote:
Op woensdag 27 juni 2012 18:54 schreef kutkloon7 het volgende:
Ik voel me hier nu niet bepaald beter door, danku
Het dictaat had ook niet veel geholpen trouwens, ik hoorde iedereen al klagen dat je er helemaal niks aan had.

Tja, maar zonder dictaat had ik denk ik ook geen voldoende gehaald hoor

. Het tentamen was vorig jaar gewoon een kwestie van het dictaat nadoen. Ik had het vak pas gevolgd als tweedejaars, wat het ook wel makkelijk maakt.

Wel kut om het overnieuw te doen trouwens, kan je weer al die verslagen gaan maken.

woensdag 27 juni 2012 @ 20:22:07 #87

#ANONIEM

quote:
Op woensdag 27 juni 2012 15:32 schreef Riparius het volgende:

[..]

Je kunt eens beginnen met de site van Dick Klingens. Hier is heel veel te vinden over vlakke meetkunde, met bewijzen, en alles in het Nederlands (hetgeen van belang is omdat je dan ook vertrouwd raakt met de unieke Nederlandse termen voor veel meetkundige begrippen). Maar let op de waarschuwing (met een knipoog naar Plato): Μηδεὶς ἀγεωμέτρητος εἰσίτω μου τὴν στέγην (laat niemand die onkundig is in de meetkunde mijn site binnengaan).

Dankjewel!

Mijn cijfer voor wiskunde B is bekend, slechts een 8..

Schriftelijk 7,8, mondeling 7,6...

woensdag 27 juni 2012 @ 20:32:29 #88

kutkloon7

quote:
Op woensdag 27 juni 2012 20:22 schreef Amoeba het volgende:

[..]

Dankjewel!

Mijn cijfer voor wiskunde B is bekend, slechts een 8..

Schriftelijk 7,8, mondeling 7,6...

Deed jij nou staatsexamen?
^{Hihi er staat sex}

woensdag 27 juni 2012 @ 20:38:22 #89

Riparius

quote:
Op woensdag 27 juni 2012 20:22 schreef Amoeba het volgende:

[..]

Dankjewel!

Om nog even terug te komen op die meetkunde opgave die je kreeg voorgeschoteld, dat was een klassieker, gebaseerd op propositie 31 uit het zesde boek van de elementen van Euclides (de examencommissie heeft dus ook niet veel fantasie). Kijk hier maar even.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

woensdag 27 juni 2012 @ 21:07:57 #90

Anoonumos

Bepaal de laatste 2 cijfers van 123^456.
Hoe pak je zo'n soort opgave aan?

woensdag 27 juni 2012 @ 21:54:09 #91

Riparius

quote:
Op woensdag 27 juni 2012 21:07 schreef Anoonumos het volgende:
Bepaal de laatste 2 cijfers van 123^456.
Hoe pak je zo'n soort opgave aan?

Beetje creatief zijn. We hebben:

123 = 41∙3

en dus:

123⁴⁵⁶ = 41⁴⁵⁶∙3⁴⁵⁶

Hiermee heb je het probleem herleid tot het bepalen van de laatste twee cijfers van 41⁴⁵⁶ en van 3⁴⁵⁶, want als je die beide weet vind je door vermenigvuldiging de laatste twee cijfers van 123⁴⁵⁶.

Verder heb je

41⁴⁵⁶ = (40 + 1)⁴⁵⁶

Zie je wat je hiermee kunt doen?

Voor machten van 3 kun je bedenken dat 3²⁰ = 3486784401 zodat het patroon van de laatste twee cijfers zich dan weer gaat herhalen. Dus kan ik meteen zeggen dat de laatste twee cijfers van 3⁴⁵⁶ hetzelfde zijn als de laatste twee cijfers van 3¹⁶ = 43046721. Nu mag je zelf weer even verder denken.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

woensdag 27 juni 2012 @ 22:30:52 #92

Bram_van_Loon

Jeff, we can!

quote:
Mijn cijfer voor wiskunde B is bekend, slechts een 8..

Schriftelijk 7,8, mondeling 7,6...

Niets mis mee, je mag daar best trots op zijn. De meetkundevraagjes zijn soms wat tricky en je moet er ook rekening mee houden dat je genaaid kan worden door de wijze van normeren, het is perfect mogelijk dat je volgens een correcte redenatie tot het juiste antwoord krijgt en dat je toch niet alle punten voor die vraag krijgt omdat de normering per vraag is opgedeeld in allerlei deelstappen, dat werkt nivellerend aangezien de zwakkere leerlingen al snel nog wat puntjes sprokkelen terwijl de goede leerlingen misschien wel stap b en c overslaan (niet expliciet opschrijven) en hierdoor wat punten mislopen. Indien de leraar zijn eigen oordeel zou mogen gebruiken in plaats van het normeringsmodel te gebruiken dan zou de standaarddeviatie waarschijnlijk wat groter zijn.
Een 8 is voor mondeling bij veel examinatoren zo'n beetje het hoogst haalbare dus dat is ook in orde.

Als je jouw examen nog eens in zou gaan kijken laat je dan weten waar je de puntjes hebt laten liggen?

ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL

woensdag 27 juni 2012 @ 22:53:30 #93

kutkloon7

quote:
Op woensdag 27 juni 2012 21:54 schreef Riparius het volgende:

[..]

Beetje creatief zijn. We hebben:

123 = 41∙3

en dus:

123⁴⁵⁶ = 41⁴⁵⁶∙3⁴⁵⁶

Hiermee heb je het probleem herleid tot het bepalen van de laatste twee cijfers van 41⁴⁵⁶ en van 3⁴⁵⁶, want als je die beide weet vind je door vermenigvuldiging de laatste twee cijfers van 123⁴⁵⁶.

Verder heb je

41⁴⁵⁶ = (40 + 1)⁴⁵⁶

Zie je wat je hiermee kunt doen?

Voor machten van 3 kun je bedenken dat 3²⁰ = 3486784401 zodat het patroon van de laatste twee cijfers zich dan weer gaat herhalen. Dus kan ik meteen zeggen dat de laatste twee cijfers van 3⁴⁵⁶ hetzelfde zijn als de laatste twee cijfers van 3¹⁶ = 43046721. Nu mag je zelf weer even verder denken.

Zou het niet makkelijker zijn om met modulorekenen te doen? Dan heb je niet zoveel inzicht nodig.

woensdag 27 juni 2012 @ 22:57:09 #94

Riparius

quote:
Op woensdag 27 juni 2012 22:53 schreef kutkloon7 het volgende:

[..]

Zou het niet makkelijker zijn om met modulorekenen te doen? Dan heb je niet zoveel inzicht nodig.

Ik denk dat het juist omgekeerd is. Als je modulair kunt rekenen stel je waarschijnlijk niet zo'n vraag.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

woensdag 27 juni 2012 @ 23:03:30 #95

kutkloon7

quote:
Op woensdag 27 juni 2012 22:57 schreef Riparius het volgende:

[..]

Ik denk dat het juist omgekeerd is. Als je kunt modulusrekenen stel je waarschijnlijk niet zo'n vraag.

Dat is waar ja. Maar zo'n vraagstuk lijkt me een prima reden om het te leren, zo moeilijk is het niet

woensdag 27 juni 2012 @ 23:14:57 #96

kutkloon7

quote:
Op woensdag 27 juni 2012 21:07 schreef Anoonumos het volgende:
Bepaal de laatste 2 cijfers van 123^456.
Hoe pak je zo'n soort opgave aan?

Hier staat wel goede uitleg voor dat soort problemen, met wat sommen (die trouwens erg veel op die vraag lijken).

woensdag 27 juni 2012 @ 23:21:12 #97

#ANONIEM

quote:
Op woensdag 27 juni 2012 22:30 schreef Bram_van_Loon het volgende:

[..]

Niets mis mee, je mag daar best trots op zijn. De meetkundevraagjes zijn soms wat tricky en je moet er ook rekening mee houden dat je genaaid kan worden door de wijze van normeren, het is perfect mogelijk dat je volgens een correcte redenatie tot het juiste antwoord krijgt en dat je toch niet alle punten voor die vraag krijgt omdat de normering per vraag is opgedeeld in allerlei deelstappen, dat werkt nivellerend aangezien de zwakkere leerlingen al snel nog wat puntjes sprokkelen terwijl de goede leerlingen misschien wel stap b en c overslaan (niet expliciet opschrijven) en hierdoor wat punten mislopen. Indien de leraar zijn eigen oordeel zou mogen gebruiken in plaats van het normeringsmodel te gebruiken dan zou de standaarddeviatie waarschijnlijk wat groter zijn.
Een 8 is voor mondeling bij veel examinatoren zo'n beetje het hoogst haalbare dus dat is ook in orde.

Als je jouw examen nog eens in zou gaan kijken laat je dan weten waar je de puntjes hebt laten liggen?

Ik krijg mijn examen niet meer te zien, maar ik kan het wel vertellen. De stappen van P passeert de evenwichtsstand op t=7,5 enzo, ik vulde direct die t waarde in. De meetkunde opgaven kreeg ik niet af en 2 vragen stuurden me het bos in (deels goed, dat wel).

donderdag 28 juni 2012 @ 13:43:16 #98

Riparius

quote:
Op woensdag 27 juni 2012 23:03 schreef kutkloon7 het volgende:

[..]

Dat is waar ja. Maar zo'n vraagstuk lijkt me een prima reden om het te leren, zo moeilijk is het niet

Dat klopt, alleen moet je dan nog wel wat handige keuzes zien te maken, waarbij een (simpele) calculator nu eindelijk eens wél van pas komt.

Omdat het er niet naar uit ziet dat Anoonumos nog reageert zal ik mijn aanpak even verder uitwerken voor eventuele andere geïnteresseerden. We hadden

41⁴⁵⁶ = (40 + 1)⁴⁵⁶

Nu bevatten alle termen van dit binomium uitgezonderd de laatste twee tenminste twee factoren 40, wat dus betekent dat alle termen, uitgezonderd de laatste twee, veelvouden zijn van 100 en daarmee geen bijdrage leveren aan de laatste twee cijfers van 41⁴⁵⁶. We kunnen dus volstaan met het optellen van de laatste twee termen van het binomium. We hebben dan

41⁴⁵⁶ = (40 + 1)⁴⁵⁶ = ... + 456∙40¹∙1⁴⁵⁵ + 1∙40⁰∙1⁴⁵⁶ = ... + 456∙40 + 1 = ... + 18241, zodat de laatste twee cijfers dus 41 zijn.

We hadden al de laatste twee cijfers van 3⁴⁵⁶, namelijk 21, en het product van 41 en 21 is 861 zodat de laatste twee cijfers van 123⁴⁵⁶ = 41⁴⁵⁶∙3⁴⁵⁶ dus ook 61 zijn.

Met modulair rekenen bedenk je dat 123 ≡ 23 (mod 100). Het is nu zaak eerst een macht van 23 te vinden waarvan het getal gevormd door de twee eindcijfers liefst zo klein mogelijk is. Met een eenvoudige calculator waarmee je gemakkelijk herhaalde vermenigvuldigingen kunt uitvoeren (ik heb de rekenmachine van Windows gebruikt) vind je dan bijvoorbeeld dat

23¹⁵ = 266635235464391245607

zodat

123⁴⁵⁶ ≡ 23⁴⁵⁶ = (23¹⁵)³⁰∙23⁶ ≡ 7³⁰∙23⁶ ≡ 49∙89 = 4361 ≡ 61 (mod 100),

en dat klopt uiteraard met wat we eerder vonden.

Als je een calculator gebruikt die niet genoeg significante cijfers heeft om 23¹⁵ of 7³⁰ = 22539340290692258087863249 te berekenen, dan gebruik je dat 7⁴ = 2401, zodat

7³⁰ = (7⁴)⁷∙7² ≡ 1⁷∙49 = 49 (mod 100).

Evenzo kun je gebruik maken van 23⁵ = 6436343 zodat

23¹⁵ = (23⁵)³ ≡ 43³ = 79507 ≡ 7 (mod 100),

en trouwens ook

23²⁰ = (23⁵)⁴ ≡ 43⁴ = 3418801 ≡ 1 (mod 100).

Een alternatieve berekening met een calculator die alleen 'kleine' getallen aankan, of met pen en papier, wordt dan:

123⁴⁵⁶ ≡ 23⁴⁵⁶ = (23²⁰)²²∙23¹⁵∙23 ≡ 1∙7∙23 = 161 ≡ 61 (mod 100).

[ Bericht 0% gewijzigd door Riparius op 28-06-2012 13:48:25 ]

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

donderdag 28 juni 2012 @ 14:16:12 #99

thabit

123 = -1 mod 4 dus 123⁴⁵⁶ = 1 mod 4.
123 = -2 mod 25 dus 123⁴⁵⁶ = (-2)⁴⁵⁶ = 2⁴⁵⁶ mod 25
Je kan de machten van 2 modulo 25 makkelijk uitrekenen: 2, 4, 8, 16, 7, 14, 3, 6, 12, 24, 23, 21, 17, 9, 18, 11, 22, 19, 13, 1. Zo vinden we een periode van 20 (met wat meer kennis over modulorekenen is overigens direct in te zien dat 2²⁰=1 mod 25 geldt, maar dat terzijde).
Dus 2⁴⁵⁶ = 2¹⁶ mod 25 = 11 mod 25 zoals we uit het rijtje kunnen afleiden.
De getallen modulo 100 die 11 mod 25 zijn, zijn 11, 36, 61, 86. Alleen 61 daarvan is 1 mod 4.

Daar zijn toch geen ingewikkelde rekenpartijen voor nodig.

donderdag 28 juni 2012 @ 14:37:21 #100

Riparius

quote:
Op donderdag 28 juni 2012 14:16 schreef thabit het volgende:
123 = -1 mod 4 dus 123⁴⁵⁶ = 1 mod 4.
123 = -2 mod 25 dus 123⁴⁵⁶ = (-2)⁴⁵⁶ = 2⁴⁵⁶ mod 25
Je kan de machten van 2 modulo 25 makkelijk uitrekenen: 2, 4, 8, 16, 7, 14, 3, 6, 12, 24, 23, 21, 17, 9, 18, 11, 22, 19, 13, 1. Zo vinden we een periode van 20 (met wat meer kennis over modulorekenen is overigens direct in te zien dat 2²⁰=1 mod 25 geldt, maar dat terzijde).
Dus 2⁴⁵⁶ = 2¹⁶ mod 25 = 11 mod 25 zoals we uit het rijtje kunnen afleiden.
De getallen modulo 100 die 11 mod 25 zijn, zijn 11, 36, 61, 86. Alleen 61 daarvan is 1 mod 4.

Daar zijn toch geen ingewikkelde rekenpartijen voor nodig.

Dat is inderdaad heel elegant, ik had er niet aan gedacht om eerst het getal mod 4 en mod 25 te bepalen. Maar ik doe dit soort dingen zelden.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

Forum Opties
Forumhop:
Hop naar:	(afkorting, bv 'KLB')

» school, studie en onderwijs

» school, studie en onderwijs