SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Waarom technische wiskunde? Je kunt ook theoretische doenquote:Op zaterdag 23 juni 2012 17:19 schreef Amoeba het volgende:
[..]
Dan moet ik wel een roostervrije dag krijgen. Voor Technische Wiskunde, is daar veel natuurkunde voor nodig? Ik zuig namelijk best wel hard in natuurkunde.
.
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Je hebt ook heel veel gratis dictaten die gewoon op de internet staan.quote:
[..]
Maak je niet druk. Je kan gewoon alvast wat boeken kopen of downloaden die ze daar of aan een andere universiteit gebruiken. Grotendeels zal je het toch zelf moeten doen, ook als je daar gaat studeren.
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Dat was al ooit aan bod gekomen. Eindhoven ligt dichtbij, evenals Nijmegen. Wiskunde en technische wiskunde zijn beide een optie, maar toch trekt de technische kant mij meer.
Verder weg studeren is voor jou geen optie omdat je liever thuis wil blijven wonen? Ik weet niet hoe de kwaliteit eventueel verschilt tussen de Nederlandse universiteiten maar het schijnt sowieso bij wiskunde zo te zijn dat de specialisaties sterk verschillen.
http://websites.math.leidenuniv.nl/algebra/
Amoeba, hier ben je vast wel eventjes zoet mee.
Zoek wat en je zal nog veel meer vinden maar maak wel af waar je mee begint.
Dat ook ja. De universiteit Leiden heeft bijv. wat dictaten die daar voor algebra worden gebruikt.quote:Je hebt ook heel veel gratis dictaten die gewoon op de internet staan.
http://websites.math.leidenuniv.nl/algebra/
Amoeba, hier ben je vast wel eventjes zoet mee.
Zoek wat en je zal nog veel meer vinden maar maak wel af waar je mee begint.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Ik wil in de vakantie m'n literatuurlijst wat bijwerken en vooral veel wiskunde. Een paar hoofdstukken wiskunde D, en zo'n dictaat bestuderen.
Hoi,
Graag wil ik een vraag stellen over het volgende:
Een miligram koolstof kun je nog net zien. Het is een schraapseltje van een potloodpunt. Een koolstofatoom heeft een massa van 2*10^-26 kg.
Hoeveel atomen bevat een milligram koolstof?
De aarde heeft een straal van 6000 km. Hoeveel koolstof atomen uit die milligram kunnen we op elke vierkante meter van het aardoppervlak leggen?
Het antwoord op de eerste vraag weet ik al, want dat is gewoon van kilo naar miligram rekenen.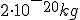
.
Maar die tweede vraag lukt me niet
. Ik had wel de omtrek berekend van de aarde dus 2*Pi*6000= 12000 Pi. Dus 12000 is de omtrek toch? Maar verder dan dit kom ik nog niet . Kan iemand me helpen? Graag wacht ik op uw reactie. Alvast bedankt voor uw antwoord.
Groet,
superky
Graag wil ik een vraag stellen over het volgende:
Een miligram koolstof kun je nog net zien. Het is een schraapseltje van een potloodpunt. Een koolstofatoom heeft een massa van 2*10^-26 kg.
Hoeveel atomen bevat een milligram koolstof?
De aarde heeft een straal van 6000 km. Hoeveel koolstof atomen uit die milligram kunnen we op elke vierkante meter van het aardoppervlak leggen?
Het antwoord op de eerste vraag weet ik al, want dat is gewoon van kilo naar miligram rekenen.
Maar die tweede vraag lukt me niet
. Ik had wel de omtrek berekend van de aarde dus 2*Pi*6000= 12000 Pi. Dus 12000 is de omtrek toch? Maar verder dan dit kom ik nog niet . Kan iemand me helpen? Graag wacht ik op uw reactie. Alvast bedankt voor uw antwoord.Groet,
superky
Je wil nu het oppervlak van de aardbol weten, niet de omtrek.
En dat wordt gegeven door 4πr2
En verder moet je eens vragen wat ze precies vragen. Je geeft namelijk tóch een verkeerd antwoord.
[ Bericht 32% gewijzigd door #ANONIEM op 23-06-2012 19:27:06 ]
En dat wordt gegeven door 4πr2
En verder moet je eens vragen wat ze precies vragen. Je geeft namelijk tóch een verkeerd antwoord.
[ Bericht 32% gewijzigd door #ANONIEM op 23-06-2012 19:27:06 ]
Tja, bij technische wiskunde mis je denk ik wel pareltjes als topologie en maattheorie.quote:
[..]
Waarom technische wiskunde? Je kunt ook theoretische doen
Jij studeert theoretische wiskunde?quote:Op zaterdag 23 juni 2012 19:21 schreef thenxero het volgende:
[..]
Tja, bij technische wiskunde mis je denk ik wel pareltjes als topologie en maattheorie.
Je brengt me toch wel erg aan het twijfelen. Maar met een studie theoretische wiskunde het bedrijfsleven ingaan is ook makkelijk?quote:
Bij TW (op de TU/e) volg je alleen Mechanica I als natuurkundevak. Geen moeilijk vak (in principe alleen herhaling van vwo-stof), maar toch hadden veel wiskundestudenten er moeite mee.quote:
[..]
Dan moet ik wel een roostervrije dag krijgen. Voor Technische Wiskunde, is daar veel natuurkunde voor nodig? Ik zuig namelijk best wel hard in natuurkunde.
The biggest argument against democracy is a five minute discussion with the average voter.
Ah, maattheorie wordt ook netjes gegeven aan de TU/e.quote:Op zaterdag 23 juni 2012 19:32 schreef Amoeba het volgende:
[..]
Je brengt me toch wel erg aan het twijfelen. Maar met een studie theoretische wiskunde het bedrijfsleven ingaan is ook makkelijk?
Zie hier , bij Keuzepakket Voortgezette Stochastiek (15 sp). "Topologie en meetkunde" en "getaltheorie" zit in keuzepakket Utrecht, dus dan sprokkel je ook nog wat theoretische vakken mee. Degelijke analyse en functionaalanalyse kan je ook nog kiezen aan de TU zie ik. En aan toegepaste vakken kan je zo'n beetje alles doen wat je maar kan bedenken.
TW lijkt me dus zeker geen slechte keuze. Uiteindelijk zal het niet zoveel uitmaken wat voor bachelor je doet, de overlap is erg groot. Het lijkt me wel aan te raden dat je met zoveel mogelijk wiskunde vakgebieden in aanraking komt in je bachelor, dan merk je vanzelf wat je het leukste vindt zodat je de juiste master kan kiezen.
Oh, en theoretische vakken doe je eigenlijk alleen maar omdat het mooi is of omdat het duidelijk de fundamenten neerlegt die je bij toegepaste vakken alleen maar gebruikt (en niet direct voor een baan in het bedrijfsleven). Maar als daar echt je passie in zit (wat ik me bij jou nog wel kan voorstellen als ik je posts zo zie) en er goed in bent, kan je natuurlijk nog wel die kant op in de academische wereld (Phd, postdoc, professor, etc
).[ Bericht 7% gewijzigd door thenxero op 23-06-2012 19:49:03 ]
Je vergeet Groepen-, Ringen-, Galois- en Getaltheorie.quote:
[..]
Tja, bij technische wiskunde mis je denk ik wel pareltjes als topologie en maattheorie.
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Klopt, die vind je niet terug in het keuzepakket van TU/e. (ik was ze niet vergeten maar het waren niet mijn favorieten, laat ik het zo zeggen)quote:
[..]
Je vergeet Groepen-, Ringen- , Galois- en Getaltheorie.
De wiskunde an sich boeit mij, ofwel het theoretische gedeelte. Maar om later toch een mooi baantje te krijgen zal men er toch ook wat mee moeten kunnen, daarom overwoog ik Technische Wiskunde.quote:
[..]
Ah, maattheorie wordt ook netjes gegeven aan de TU/e.
Zie hier , bij Keuzepakket Voortgezette Stochastiek (15 sp). "Topologie en meetkunde" en "getaltheorie" zit in keuzepakket Utrecht, dus dan sprokkel je ook nog wat theoretische vakken mee. Degelijke analyse en functionaalanalyse kan je ook nog kiezen aan de TU zie ik. En aan toegepaste vakken kan je zo'n beetje alles doen wat je maar kan bedenken.
TW lijkt me dus zeker geen slechte keuze. Uiteindelijk zal het niet zoveel uitmaken wat voor bachelor je doet, de overlap is erg groot. Het lijkt me wel aan te raden dat je met zoveel mogelijk wiskunde vakgebieden in aanraking komt in je bachelor, dan merk je vanzelf wat je het leukste vindt zodat je de juiste master kan kiezen.
Oh, en theoretische vakken doe je eigenlijk alleen maar omdat het mooi is of omdat het duidelijk de fundamenten neerlegt die je bij toegepaste vakken alleen maar gebruikt (en niet direct voor een baan in het bedrijfsleven). Maar als daar echt je passie in zit (wat ik me bij jou nog wel kan voorstellen als ik je posts zo zie) en er goed in bent, kan je natuurlijk nog wel die kant op in de academische wereld (Phd, postdoc, professor, etc
Oh oke, puur voor de baan hoef je het niet te doen. Uiteindelijk zal je (denk ik) toch een master doen. Het is veel meer van belang wat je dan gaat uitspoken. Er zijn zat toegepaste vakken te kiezen, en je kan in je master ook ruim een half jaar stage lopen bij een bedrijf (bij theoretische wiskunde). Dan heb je je dosis praktijk ook wel gehad.quote:
[..]
De wiskunde an sich boeit mij, ofwel het theoretische gedeelte. Maar om later toch een mooi baantje te krijgen zal men er toch ook wat mee moeten kunnen, daarom overwoog ik Technische Wiskunde.
@Amoeba: ik beantwoord je vraag maar even hier, want dan hebben anderen er misschien ook (ooit) nog eens iets aan.
Probleem: primitiveer sin4x
Oplossing: we maken gebruik van de identiteiten sin2α = ½(1 - cos 2α) en cos2α = ½(1 + cos 2α)
sin4x = (½∙(1 - cos 2x))2
sin4x = ¼∙(1 - 2∙cos 2x + cos22x)
sin4x = ¼∙(1 - 2∙cos 2x + ½(1 + cos 4x))
sin4x = ¼∙(1 - 2∙cos 2x + ½ + ½∙cos 4x)
sin4x = ¼ - ½∙cos 2x + 1/8 + 1/8∙cos 4x
sin4x = 3/8 - ½∙cos 2x + 1/8∙cos 4x
Ergo:
∫ sin4x∙dx = ∫ (3/8 - ½∙cos 2x + 1/8∙cos 4x)dx = 3/8∙x -¼∙sin 2x + 1/32∙sin 4x + C
Probleem: primitiveer sin4x
Oplossing: we maken gebruik van de identiteiten sin2α = ½(1 - cos 2α) en cos2α = ½(1 + cos 2α)
sin4x = (½∙(1 - cos 2x))2
sin4x = ¼∙(1 - 2∙cos 2x + cos22x)
sin4x = ¼∙(1 - 2∙cos 2x + ½(1 + cos 4x))
sin4x = ¼∙(1 - 2∙cos 2x + ½ + ½∙cos 4x)
sin4x = ¼ - ½∙cos 2x + 1/8 + 1/8∙cos 4x
sin4x = 3/8 - ½∙cos 2x + 1/8∙cos 4x
Ergo:
∫ sin4x∙dx = ∫ (3/8 - ½∙cos 2x + 1/8∙cos 4x)dx = 3/8∙x -¼∙sin 2x + 1/32∙sin 4x + C
Waarom? Print de post maar even uit, lijkt me duidelijk. En ja, zeg maar tegen die docent dat hij z'n goniometrische identiteiten moet kennen.quote:
Super, misschien zou je het aan mijn wiskunde docent uit willen leggen?
O ja, en voor ∫ sinnxdx kun je in de leer bij .
Was een geintje.. Ik doelde er eigenlijk op dat het niet mijn vraag was aangezien ik het via de reductie formule had gedaan, maar zijn vraag.
Alhoewel ik op een vorm van:
[tex] \frac{1}{8}(3x - 2cos(x)sin^3(x) - 3sin(\frac{1}{2}x))[/tex]
uitkwam.
Maar dat was in de haast zonder het even na te kijken. Volgens mij klopt dit nml even niet.
[ Bericht 43% gewijzigd door #ANONIEM op 23-06-2012 20:33:16 ]
Alhoewel ik op een vorm van:
[tex] \frac{1}{8}(3x - 2cos(x)sin^3(x) - 3sin(\frac{1}{2}x))[/tex]
uitkwam.
Maar dat was in de haast zonder het even na te kijken. Volgens mij klopt dit nml even niet.
[ Bericht 43% gewijzigd door #ANONIEM op 23-06-2012 20:33:16 ]
Graag wil ik nog één vraagje stellen over het volgende:
Het wereldrecord op de 100 m hardlopen is kort geleden gebracht op 9,79 s. Heeft de atleet op enig moment gedurende zijn race met een snelheid groter dan 40 km per uur gelopen?
Ik weet al dat een snelheid van 1 meter per seconde overeen komt met een snelheid van 3,6 kilometer per uur. Maar hoe ik het daarna moet aanpakken weet ik niet. Ik kom nog intelligentie tekort... Kan iemand me weer helpen? Alvast bedankt voor uw antwoord 
Het wereldrecord op de 100 m hardlopen is kort geleden gebracht op 9,79 s. Heeft de atleet op enig moment gedurende zijn race met een snelheid groter dan 40 km per uur gelopen?
Ik weet al dat een snelheid van 1 meter per seconde overeen komt met een snelheid van 3,6 kilometer per uur. Maar hoe ik het daarna moet aanpakken weet ik niet
. Ik kom nog intelligentie tekort... Kan iemand me weer helpen? Alvast bedankt voor uw antwoord
Als je jezelf nu bedenkt dat als hij constant 40 km/h zou lopen, zou hij dan in 9,79 seconden 100 meter gelopen hebben?
[ Bericht 1% gewijzigd door #ANONIEM op 23-06-2012 20:31:54 ]
[ Bericht 1% gewijzigd door #ANONIEM op 23-06-2012 20:31:54 ]
Dat is niet correct. Controleer maar even in WolframAlpha.quote:
Was een geintje.. Ik doelde er eigenlijk op dat het niet mijn vraag was aangezien ik het via de reductie formule had gedaan, maar zijn vraag.
Alhoewel ik op een vorm van:
uitkwam.
Ik denk dat je ervan uit mag/moet gaan dat zijn snelheid lineair stijgt, anders kan je het niet echt uitrekenen. Weet je wat over integralen/afgeleiden? Die heb je namelijk nodig.quote:
Graag wil ik nog één vraagje stellen over het volgende:
Het wereldrecord op de 100 m hardlopen is kort geleden gebracht op 9,79 s. Heeft de atleet op enig moment gedurende zijn race met een snelheid groter dan 40 km per uur gelopen?
Ik weet al dat een snelheid van 1 meter per seconde overeen komt met een snelheid van 3,6 kilometer per uur. Maar hoe ik het daarna moet aanpakken weet ik niet
Ja ik zag net ook al een foutje op papier staan. Mijn excuses.quote:
[..]
Dat is niet correct. Controleer maar even in WolframAlpha.
40 km/h = 40/3,6 = 11,11 m/s * 9,79 is ongeveer 108,78. Dat schiet dus ook niet op.quote:Op zaterdag 23 juni 2012 20:33 schreef kutkloon7 het volgende:
[..]
Ik denk dat je ervan uit mag/moet gaan dat zijn snelheid lineair stijgt, anders kan je het niet echt uitrekenen. Weet je wat over integralen/afgeleiden? Die heb je namelijk nodig.
Je vraagstelling is dus onvolledig, wat was de extra informatie?
Het ligt eraan wat je het meest trekt. Beide programma's zijn prima, en er is veel overlap zoals ik al zei... bij technische wiskunde wat meer nadruk op modelleren (wel nuttig want dat zal je in banen vaak gebruiken, maar wiskundig gezien misschien wat minder interessant), bij wiskunde wat meer nadruk op theorie (leuk maar vaak niet direct "nuttig").quote:
Dus je raadt mij aan toch theoretische wiskunde te proberen?
Dat lijkt me onrealistisch. Bovendien is dat niet uit de vraagstelling af te leiden. Gegeven is dat hij 9,79 sec. deed over 100 m zodat de gemiddelde snelheid dus ((100/9,79)*3600)/1000 km/h bedroeg, wat neerkomt op ca. 36,77 km/h. De vraag of hij op enig moment harder heeft gelopen dan 40 km/h is niet te beantwoorden.quote:
[..]
Ik denk dat je ervan uit mag/moet gaan dat zijn snelheid lineair stijgt, anders kan je het niet echt uitrekenen. Weet je wat over integralen/afgeleiden? Die heb je namelijk nodig.
[ Bericht 0% gewijzigd door Riparius op 23-06-2012 21:02:57 ]
=
Ergo
Ik primitiveerde net sin2(x) met partieel integreren, toen kwam ik op:
[ Bericht 0% gewijzigd door #ANONIEM op 23-06-2012 20:45:08 ]
Nee, dat laatste klopt niet.quote:
=
Ergo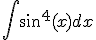
Ik primitiveerde net sin2(x) met partieel integreren, toen kwam ik op:uit, klopt dit?
[ Bericht 0% gewijzigd door Riparius op 23-06-2012 20:57:40 ]
Ah zo. Ik dacht dat je de integraal zelf via partieel integreren probeerde op te lossen, en niet met een kant en klare recursieve formule.quote:
Maar bedenk nu eerst maar eens hoe je sin2x primitiveert. Ken je identiteiten ...
Wat is daar fout aan? Ik kom weer op hetzelfde antwoord uit.
Zelfs WolframAlpha geeft me gelijk, enkel kon ik verder vereenvoudigen naar 1/2x -1/2cos(x)sin(x). Want sin(2x) = 2cos(x)sin(x)
Of bedoel je via partieel integreren? In dat geval ga ik nog eens aan het schrijven.
[ Bericht 1% gewijzigd door #ANONIEM op 23-06-2012 21:05:02 ]
Zelfs WolframAlpha geeft me gelijk, enkel kon ik verder vereenvoudigen naar 1/2x -1/2cos(x)sin(x). Want sin(2x) = 2cos(x)sin(x)
Of bedoel je via partieel integreren? In dat geval ga ik nog eens aan het schrijven.
[ Bericht 1% gewijzigd door #ANONIEM op 23-06-2012 21:05:02 ]
Zo praten we een beetje langs elkaar heen. Toen ik hierboven zei dat je primitieve van sin2x niet klopte doelde ik op de uitdrukking die je daar geeft, en die is gewoon fout.quote:
Wat is daar fout aan? Ik kom weer op hetzelfde antwoord uit.
goeien foto van een Galaxy S3
Correct, mag ik hopen?
ik hoop dat jullie geen nekklachten krijgen
[ Bericht 28% gewijzigd door #ANONIEM op 23-06-2012 21:20:00 ]
Ja, wel een beetje een rare notatie zo met die d'tjes.quote:
[ afbeelding ]
goeien foto van een Galaxy S3
Correct, mag ik hopen?
Wát?quote:
[..]
Ja, wel een beetje een rare notatie zo met die d'tjes.
Mij werd eigenlijk altijd aangeleerd dat het voor *de afgeleide van stond. Maar is het dan per definitie fout?quote:
Nee, je eigen notatie gebruiken is nooit fout, hooguit onhandig voor andere lezers (alhoewel het hier wel duidelijk is). d/dx of een accentje is standaard.quote:
[..]
Mij werd eigenlijk altijd aangeleerd dat het voor *de afgeleide van stond. Maar is het dan per definitie fout?
jaquote:
[..]
Zo praten we een beetje langs elkaar heen. Toen ik hierboven zei dat je primitieve van sin2x niet klopte doelde ik op de uitdrukking die je daar geeft, en die is gewoon fout.
Je moet wel je haakjes correct gebruiken. En eigen notaties zijn niet altijd een goed idee, vooral niet als je niet consequent bent. De regel voor partieel integreren luidt symbolisch:quote:
[..]
Mij werd eigenlijk altijd aangeleerd dat het voor *de afgeleide van stond. Maar is het dan per definitie fout?
∫ u∙dv = u∙v - ∫ v∙du
Welnu, in jouw geval heb je u = sin(x), dv = sin(x)∙dx, en dus du = cos(x)∙dx, v = -cos(x). Dit geeft:
∫ sin(x)∙d(-cos(x)) = -sin(x)∙cos(x) - ∫ -cos(x)∙d(sin(x))
Fck it, ik geef je gelijk. Ik zal er op letten.quote:
[..]
Je moet wel je haakjes correct gebruiken. En eigen notaties zijn niet altijd een goed idee, vooral niet als je niet consequent bent. De regel voor partieel integreren luidt symbolisch:
∫ u∙dv = u∙v - ∫ v∙du
Welnu, in jouw geval heb je u = sin(x), dv = sin(x)∙dx, en dus du = cos(x)∙dx, v = -cos(x). Dit geeft:
∫ sin(x)∙d(-cos(x)) = -sin(x)∙cos(x) - ∫ -cos(x)∙d(sin(x))
[ Bericht 9% gewijzigd door #ANONIEM op 23-06-2012 21:46:44 ]
Afgeleiden ken ik en ook de regels (bijv. productregel, kettingregel, quotiëntregel etc.) Maar hoe pak ik het aan? Wat moet ik als eerst doen en wat daarna?quote:
[..]
Ik denk dat je ervan uit mag/moet gaan dat zijn snelheid lineair stijgt, anders kan je het niet echt uitrekenen. Weet je wat over integralen/afgeleiden? Die heb je namelijk nodig.
Ik zou zeggenquote:
[..]
∫ sin(x)∙d(-cos(x)) = -sin(x)∙cos(x) - ∫ -cos(x)∙d(sin(x))
∫ sin(x)∙(-cos(x))' dx = -sin(x)∙cos(x) - ∫ -cos(x)∙(sin(x))' dx
Moeilijk zo te zeggen... geef eens een voorbeeld waar je twijfelt over de volgorde.quote:
[..]
Afgeleiden ken ik en ook de regels (bijv. productregel, kettingregel, quotiëntregel etc.) Maar hoe pak ik het aan? Wat moet ik als eerst doen en wat daarna?
