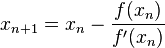SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



uh? ik wil gewoon graag een nummer ipv q. dat nummer is 0.02003
"Vanity, definitely my favorite sin. . . ."


steek maar meer moeite in het stellen van je vraag
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Je bedoeltquote:Op zaterdag 28 januari 2012 21:24 schreef One_conundrum het volgende:
uh? ik wil gewoon graag een nummer ipv q. dat nummer is 0.02003
Want dan is
Of bedoel je
Erg duidelijk ben je niet
Inderdaad.quote:Op zaterdag 28 januari 2012 21:30 schreef GlowMouse het volgende:
steek maar meer moeite in het stellen van je vraag


haha, Ik had niet verwacht dat mijn vraag zo onduidelijk was.quote:Op zaterdag 28 januari 2012 21:30 schreef GlowMouse het volgende:
steek maar meer moeite in het stellen van je vraag
Hmm er ontbreek natuurlijk iets. stom. Ik dacht dat dit stuk wel genoeg was...
nog es kijken dan
"Vanity, definitely my favorite sin. . . ."


100 - 1e -(0.04/12) = 100e -q/2
Zo dus. Nu is het logischer toch? hoe los ik nu q op?
Sorry van mijn eerdere fuck-up
Zo dus. Nu is het logischer toch? hoe los ik nu q op?
Sorry van mijn eerdere fuck-up
"Vanity, definitely my favorite sin. . . ."


Ik zal eens kijken 
[edit]
Zie voor het isoleren van q mijn post hierboven en zie 100-e-0.04/12 als a, dan:
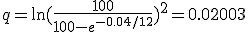
Ik heb geen GR bij de hand en geen zin om Matlab te starten, dus dat moet je zelf even intoetsen
[ Bericht 35% gewijzigd door zoem op 28-01-2012 22:22:08 ]
[edit]
Zie voor het isoleren van q mijn post hierboven en zie 100-e-0.04/12 als a, dan:
Ik heb geen GR bij de hand en geen zin om Matlab te starten, dus dat moet je zelf even intoetsen
[ Bericht 35% gewijzigd door zoem op 28-01-2012 22:22:08 ]


hmm het komt niet echt uit, ik krijg niet echt 0.02etc uit mijn GR..
het moet dus zijn uuuh
100 - 1e-(0.04/12) = 100e -(q/2)
99.003etc = 100e -(q/2)
het moet dus zijn uuuh
100 - 1e-(0.04/12) = 100e -(q/2)
99.003etc = 100e -(q/2)
"Vanity, definitely my favorite sin. . . ."


Je weet dat je ook lijntjes kan plotten op je GR?
y1 = 100e -(q/2)
y2 = 100 - 1e-(0.04/12)
Dan kun je het verloop van de vergelijking zien en met intersect heb je ook je antwoord
[edit]
Ah ik zie ik dat ik ben vergeten een 2 van de 1/2 te maken toen ik het naar "rechts" gooide.
Even fixen hierboven
[ Bericht 27% gewijzigd door zoem op 28-01-2012 22:21:27 ]
y1 = 100e -(q/2)
y2 = 100 - 1e-(0.04/12)
Dan kun je het verloop van de vergelijking zien en met intersect heb je ook je antwoord
[edit]
Ah ik zie ik dat ik ben vergeten een 2 van de 1/2 te maken toen ik het naar "rechts" gooide.
Even fixen hierboven
[ Bericht 27% gewijzigd door zoem op 28-01-2012 22:21:27 ]


99.003etc = 100e -(q/2)quote:Op zaterdag 28 januari 2012 22:07 schreef One_conundrum het volgende:
hmm het komt niet echt uit, ik krijg niet echt 0.02etc uit mijn GR..
het moet dus zijn uuuh
100 - 1e-(0.04/12) = 100e -(q/2)
99.003etc = 100e -(q/2)
99.003etc/100 = e -(q/2)
ln 99.003etc/100 = -(q/2)
-2*(ln 99.003etc/100) = q
De truc is dus om beide kanten maal ln te doen en dan valt de e weg.


Weer ff een vraag over statistiek:
5. Bij een tweezijdige toetsing van een H0 wordt een Z-waarde gevonden van 1,72. Wat zal er met de H0 gebeuren als je toets bij een alfa van 5 %?
a) niet verwerpen, want de p-waarde zal kleiner zijn dan alfa
b) niet verwerpen, want de gevonden z-waarde is kleiner dan de kritieke z-waarde
c) zowel a als b
d) noch a, noch b
Ik heb opgezocht de kans die bij de Z-waarde 1,72 hoort; aflezen in tabel = 0.9564, dan
1 - 0.9564 = 0.0436. De significantie waarde is 0.05, 0,0436 is kleiner als de alfa van 5%, dus
H0 verwerpen lijkt me.. of maak ik hier een denkfout?
Het antwoord is namelijk B.. dan heb ik nog een vraag; hoe kan je weten aan de hand van deze gegevens dat de z-waarde kleiner is dan de kritieke z-waarde?
Geldt eigenlijk precies hetzelfde verhaal bij deze vraag:
6. Bij een rechtzijdige toetsing van een H0 wordt een Z-waarde gevonden van 1,84. Wat zal er met de H0 gebeuren als je toets bij een alfa van 1 %?
a) niet verwerpen, want de p-waarde zal kleiner zijn dan alfa
b) niet verwerpen, want de gevonden z-waarde is kleiner dan de kritieke z-waarde
c) zowel a als b
d) noch a, noch b
Z waarde is hierbij 0.9664 --> 1 - 0.9664 = 0.0336
Wie o wie kan mij helpen???
5. Bij een tweezijdige toetsing van een H0 wordt een Z-waarde gevonden van 1,72. Wat zal er met de H0 gebeuren als je toets bij een alfa van 5 %?
a) niet verwerpen, want de p-waarde zal kleiner zijn dan alfa
b) niet verwerpen, want de gevonden z-waarde is kleiner dan de kritieke z-waarde
c) zowel a als b
d) noch a, noch b
Ik heb opgezocht de kans die bij de Z-waarde 1,72 hoort; aflezen in tabel = 0.9564, dan
1 - 0.9564 = 0.0436. De significantie waarde is 0.05, 0,0436 is kleiner als de alfa van 5%, dus
H0 verwerpen lijkt me.. of maak ik hier een denkfout?
Het antwoord is namelijk B.. dan heb ik nog een vraag; hoe kan je weten aan de hand van deze gegevens dat de z-waarde kleiner is dan de kritieke z-waarde?
Geldt eigenlijk precies hetzelfde verhaal bij deze vraag:
6. Bij een rechtzijdige toetsing van een H0 wordt een Z-waarde gevonden van 1,84. Wat zal er met de H0 gebeuren als je toets bij een alfa van 1 %?
a) niet verwerpen, want de p-waarde zal kleiner zijn dan alfa
b) niet verwerpen, want de gevonden z-waarde is kleiner dan de kritieke z-waarde
c) zowel a als b
d) noch a, noch b
Z waarde is hierbij 0.9664 --> 1 - 0.9664 = 0.0336
Wie o wie kan mij helpen???


Er is een verschil tussen een tweezijdige en een enkelzijdige toetsing.
Bij een tweezijdige toetsing kan je z verwerpen als het > 1.96 of <-1.96 is. Bij een enkelzijdig toetsing mag je z verwerpen als het > 1.645 of < -1.645 bij een alfa van 0.05.
Zoek de formules op in de slides of in je boek.
B is inderdaad correct.
Bij een tweezijdige toetsing kan je z verwerpen als het > 1.96 of <-1.96 is. Bij een enkelzijdig toetsing mag je z verwerpen als het > 1.645 of < -1.645 bij een alfa van 0.05.
Zoek de formules op in de slides of in je boek.
B is inderdaad correct.


"Z-waarde is (in absolute waarde) kleiner dan de kritieke z-waarde" en "p-waarde is groter dan alfa" zijn hier equivalente uitspraken.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Bedankt Zoem en Hattricker. Ik zal er vanaaf weer naar kijken.
x
x
"Vanity, definitely my favorite sin. . . ."


Ik heb een bepaalde functie sqrt ( xa + yb) , x,y>0 Hiervan moet ik aan de hand van de definietheid v/d hessian bepalen voor welke a,b (in R2) deze functie convex dan wel concaaf is. Hessian is te bepalen, dat zijn de 2e orde partiele afgeleiden. Deze zijn makkelijk te bepalen met mathematica.
Voor: strict convex moet gelden dat: hessian positief definiet
convex H pos. semidef
Concaaf/strict concaaf evenzo maar dan negatief
Om nu verder te kijken voor welke a & b alle entries groter/gelijk 0 zijn voor positief semidefiniet, respectievelijk kleiner/gelijk 0 voor negatief semidefiniet, lukt me niet. De 2e orde partiele afgeleiden zijn vrij gecompliceerde functies, waar mathematica zo geen raad mee weet. Iemand een tip hoe verder te gaan?
Voor: strict convex moet gelden dat: hessian positief definiet
convex H pos. semidef
Concaaf/strict concaaf evenzo maar dan negatief
Om nu verder te kijken voor welke a & b alle entries groter/gelijk 0 zijn voor positief semidefiniet, respectievelijk kleiner/gelijk 0 voor negatief semidefiniet, lukt me niet. De 2e orde partiele afgeleiden zijn vrij gecompliceerde functies, waar mathematica zo geen raad mee weet. Iemand een tip hoe verder te gaan?


Zo lastig is het niet. De dubbele afgeleide naar a is positief als
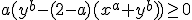
De determinant van de Hessiaan is positief als
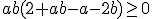
Dit kun je makkelijk zelf controleren door te gebruiken dat
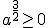
voor elke a. Bij de Hessiaan kun je ook nog een factor
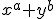
herkennen.
De determinant van de Hessiaan is positief als
Dit kun je makkelijk zelf controleren door te gebruiken dat
voor elke a. Bij de Hessiaan kun je ook nog een factor
herkennen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik bepaal nu de Hessiaan twee x met partieel afgeleiden naar 2 * x , xy, yx en 2*y. De hessiaan moet dus worden genomen met a & b als variabelen?
Thanks!
Thanks!


Ik bedoelde naar x, we doen hetzelfde 
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Zie alleen niet in hoe jij er vanaf hier bij komt dat deze 2e afgeleide positief (> of >= 0?) is wanneer
a(yb - (2-a) * (xa + yb)) .= 0 is. Die tweede regel (wanneer de determinant van de hessian positief is) kan ik ook niet achterhalen hoe je daarbij komt


Vanaf daar zou het mij ook niet lukken, dat is niet te lezen. Maar ik zie al dingen staan met ^{3/2} en een wortel, daarvan weet je dat het niet negatief is.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Sorry voor de onduidelijke post..
Maar kom er nog niet uit hoe jij vanuit:
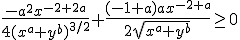
tot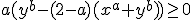 komt?
komt?
En hoe kun je deze dan verder oplosssen voor alle waarden van a&b?
Dat snap ik dus voor de determinant van de gehele hessiaan ook niet, alleen waarschijnlijk snap ik die wel als ik deze eerste snap! bedankt alvast!
Maar kom er nog niet uit hoe jij vanuit:
tot
En hoe kun je deze dan verder oplosssen voor alle waarden van a&b?
Dat snap ik dus voor de determinant van de gehele hessiaan ook niet, alleen waarschijnlijk snap ik die wel als ik deze eerste snap! bedankt alvast!


Voor strict concaaf moeten de determinant en de eigenwaardes van de Hessiaan positief zijn. Waarom dan het gelijk-aan-of-groter teken? Of is dit nog niet de (juiste) oplossing voor het strict geval?


Die breuk kun je optellen door de noemers gelijk te maken. a-2 ziet er bovendien makkelijker uit dan -2+a. Daarna kun je zien dat de noemer positief is, en concludeer je dat de teller positief moet zijn. In de teller herken je nog een factor
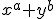
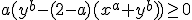
kun je schrijven als:
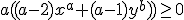
Wat b is maakt hier niet zo gek veel uit. Je kunt onderscheid maken tussen b=0 en b>0.
- Voor strict convex moet de dubbele afgeleide naar x strict positief zijn en de determinant ook.
- Voor gewoon convex moet ook de dubbele afgeleide naar y niet-negatief zijn.
Maar het probleem zat hem niet in de criteria
[ Bericht 0% gewijzigd door GlowMouse op 29-01-2012 22:59:53 ]
kun je schrijven als:
Wat b is maakt hier niet zo gek veel uit. Je kunt onderscheid maken tussen b=0 en b>0.
Ik ben inderdaad niet helemaal netjes met de tekens. Eigenlijk moet je de volgende twee aanpassingen doen tov wat ik deed:quote:Op zondag 29 januari 2012 22:47 schreef zoem het volgende:
Voor strict concaaf moeten de determinant en de eigenwaardes van de Hessiaan positief zijn. Waarom dan het gelijk-aan-of-groter teken? Of is dit nog niet de (juiste) oplossing voor het strict geval?
- Voor strict convex moet de dubbele afgeleide naar x strict positief zijn en de determinant ook.
- Voor gewoon convex moet ook de dubbele afgeleide naar y niet-negatief zijn.
Maar het probleem zat hem niet in de criteria
[ Bericht 0% gewijzigd door GlowMouse op 29-01-2012 22:59:53 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Nouja, als het groter of gelijk aan 0 is dan kan het nog wel convex zijn maar dan is het niet meer positief definiet. Maar dat heeft niets met deze opdracht te maken natuurlijk 
Ik denk dat als je de analytische vergelijkingen hebt, je vast wel elementen kan wegstrepen omdat deze toch positief zijn (zoals je zelf net al zei GM). Dingen als worteltrekken en even machten.
Ik denk dat als je de analytische vergelijkingen hebt, je vast wel elementen kan wegstrepen omdat deze toch positief zijn (zoals je zelf net al zei GM). Dingen als worteltrekken en even machten.


En allerlaatste vraag, hoe kom jij vanaf die (in mijn ogen) zeer complexe determinant van de Hessiaan tot ab(2+ab-a-2b) > 0 ? Bedankt voor de hulp


1/16 xa-2yb-2 wegdelen, ab buiten haakjes halen, xa+yb wegdelen, nog een keer door 2 delen, nog een xa+yb wegdelen 
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


12) Een onderzoeker voert een meta-analyse uit naar de correlatie tussen intelligentie van
Nederlandse ouders en dat van hun kinderen. Na combinatie van gegevens van 20
onderzoeken blijkt de correlatie tussen ouders en kinderen 0.75 te zijn, met een 95%
betrouwbaarheidsinterval dat loopt van [ 0.73 ; 0.77 ]. Welke conclusie kan op grond van
deze bevinding worden getrokken?
a) Er is waarschijnlijk geen verband tussen intelligentie van Nederlandse ouders en
hun kinderen
b) Er is waarschijnlijk een verband tussen de intelligentie van Nederlandse ouders en
hun kinderen, maar over de sterkte van dit verband valt niets te zeggen
c) Er is waarschijnlijk een verband tussen de intelligentie van Nederlandse ouders en
hun kinderen, en dit verband is tamelijk sterk
d) Er kan geen conclusie getrokken worden, omdat onbekend is hoe groot de
steekproeven van de 20 onderzoeken waren
Wie kan mij uitleggen wat het antwoord op deze vraag is en waarom?
Nederlandse ouders en dat van hun kinderen. Na combinatie van gegevens van 20
onderzoeken blijkt de correlatie tussen ouders en kinderen 0.75 te zijn, met een 95%
betrouwbaarheidsinterval dat loopt van [ 0.73 ; 0.77 ]. Welke conclusie kan op grond van
deze bevinding worden getrokken?
a) Er is waarschijnlijk geen verband tussen intelligentie van Nederlandse ouders en
hun kinderen
b) Er is waarschijnlijk een verband tussen de intelligentie van Nederlandse ouders en
hun kinderen, maar over de sterkte van dit verband valt niets te zeggen
c) Er is waarschijnlijk een verband tussen de intelligentie van Nederlandse ouders en
hun kinderen, en dit verband is tamelijk sterk
d) Er kan geen conclusie getrokken worden, omdat onbekend is hoe groot de
steekproeven van de 20 onderzoeken waren
Wie kan mij uitleggen wat het antwoord op deze vraag is en waarom?


Ik ben geen statistiek expert maar ik ga voor (c). De correlatie zit altijd tussen -1 en 1. Als het significant van 0 verschilt dan kan je spreken van correlatie. In (c) staat nog een woordje waarschijnlijk, omdat een statistische test altijd heel ver van de werkelijke waarde kan zitten (bijvoorbeeld doordat je niet willekeurig genoeg mensen hebt gekozen). Dus zeker ben je nooit.
(a) is pure onzin, (b) is onzin omdat de correlatie een maat is voor de sterkte. Bij (d) is er op zich wel het punt dat je steekproef groot genoeg moet zijn, maar omdat het confidence interval al [ 0.73 ; 0.77 ] is, is je steekproef kennelijk groot genoeg om te concluderen dat de correlatie significant groter dan 0 is.
(a) is pure onzin, (b) is onzin omdat de correlatie een maat is voor de sterkte. Bij (d) is er op zich wel het punt dat je steekproef groot genoeg moet zijn, maar omdat het confidence interval al [ 0.73 ; 0.77 ] is, is je steekproef kennelijk groot genoeg om te concluderen dat de correlatie significant groter dan 0 is.


a en d wegstrepen is simpel:
a. Zonder verband is de correlatie 0. Op grond van het betrouwbaarheidsinterval kun je de nulhypothese dat de correlatie 0 is, verwerpen.
d. de grootte van de steekproef zit verwerkt in de breedte van het betrouwbaarheidsinterval
Dan resteert de vraag hoe groot het verband is. Ik vind 'tamelijk sterk' een vaag begrip, maar dat er niets over valt te zeggen is ook niet waar (hoe groter de correlatie, hoe sterk het verband). Ik zou zeggen dat geen enkel antwoord echt goed is, maar c is de minst foute.
a. Zonder verband is de correlatie 0. Op grond van het betrouwbaarheidsinterval kun je de nulhypothese dat de correlatie 0 is, verwerpen.
d. de grootte van de steekproef zit verwerkt in de breedte van het betrouwbaarheidsinterval
Dan resteert de vraag hoe groot het verband is. Ik vind 'tamelijk sterk' een vaag begrip, maar dat er niets over valt te zeggen is ook niet waar (hoe groter de correlatie, hoe sterk het verband). Ik zou zeggen dat geen enkel antwoord echt goed is, maar c is de minst foute.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hoe duid je de index van het minimum van een rij getallen aan in wiskundige notatie? Meer specifiek, ik heb een matrix R en voor gegeven kolom k, zoek ik het minimum van die vector en daar weer de index j van.
Er staat me iets bij dat je min met de gewenste index letter er onder schrijft maar ik kan het niet terugvinden.
Ik heb nu dit
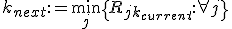
[ Bericht 14% gewijzigd door synthesix op 30-01-2012 12:42:08 ]
Er staat me iets bij dat je min met de gewenste index letter er onder schrijft maar ik kan het niet terugvinden.
Ik heb nu dit
[ Bericht 14% gewijzigd door synthesix op 30-01-2012 12:42:08 ]


Afhankelijk van je definitie van argmin moet je nog wat doen met een niet-uniek minimum.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Iemand enig idee hoe deze opgelost kan worden?
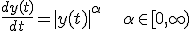
[ Bericht 2% gewijzigd door 123hopsaflops op 03-02-2012 12:27:04 ]
[ Bericht 2% gewijzigd door 123hopsaflops op 03-02-2012 12:27:04 ]


n/m
[ Bericht 73% gewijzigd door GlowMouse op 03-02-2012 12:39:14 ]
[ Bericht 73% gewijzigd door GlowMouse op 03-02-2012 12:39:14 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


verbeterdquote:Op vrijdag 3 februari 2012 12:22 schreef GlowMouse het volgende:
Is y afhankelijk van t?
Rare notatie van een interval.
Als je onderscheid maakt tussen y>=0 en y<0 dan is het toch wel te doen? Alleen opletten bij y=0 wanneer 0<alpha<=1.


Wat gebeurt er met je meetfout als je de meting een aantal keer herhaalt en dan het gemiddelde neemt? Bijvoorbeeld als ik een meetfout van 0,5 cm bij één meting heb en de meting 10x doe en dan het gemiddelde neem.


Is de meetfout systematisch of willekeurig? Is die altijd precies 5mm?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Mits de meetfouten onafhankelijk zijn.quote:Op zondag 5 februari 2012 23:19 schreef twaalf het volgende:
Nou ja, je zit erboven of eronder, dus je krijgt iets binomiaals denk ik, 10 trekkingen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Laat A en B 2x2 matrices zijn met de determinanten |A|=4 en |B|=7
ik weet dat |A|+|B| niet gelijk is aan |A+B| maar wat zijn de verschillen dan?
Is |A|+|B|=11 of is |A+B|=11??
Is |A+B| dan eerst de A+B matrices bij elkaar optellen en daar de determinant van ofzo?? Ik heb geen idee..
ik weet dat |A|+|B| niet gelijk is aan |A+B| maar wat zijn de verschillen dan?
Is |A|+|B|=11 of is |A+B|=11??
Is |A+B| dan eerst de A+B matrices bij elkaar optellen en daar de determinant van ofzo?? Ik heb geen idee..


precies, dat staat erquote:Op donderdag 9 februari 2012 13:43 schreef bezemsteeltaart het volgende:
Is |A+B| dan eerst de A+B matrices bij elkaar optellen en daar de determinant van?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


ik zou twee voorbeeldmatrices maken en het dan allebei uitproberenquote:Op donderdag 9 februari 2012 13:43 schreef bezemsteeltaart het volgende:
Laat A en B 2x2 matrices zijn met de determinanten |A|=4 en |B|=7
ik weet dat |A|+|B| niet gelijk is aan |A+B| maar wat zijn de verschillen dan?
Is |A|+|B|=11 of is |A+B|=11??
Is |A+B| dan eerst de A+B matrices bij elkaar optellen en daar de determinant van ofzo?? Ik heb geen idee..
let er op dat je geen 0 invoert op x_12 en x_21
(met die laatste tip zou je al moeten zien waar het mis gaat)


Ik moet bewijzen dat
![\lim_{n \to \infty}{x_n}=\sqrt[3]{A}](https://forum.fok.nl/lib/mimetex.cgi?%5Clim_%7Bn%20%5Cto%20%5Cinfty%7D%7Bx_n%7D%3D%5Csqrt%5B3%5D%7BA%7D)
als
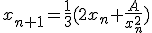
Kan iemand me een aanwijzing geven? Ik kan wel aantonen dat als
![x_n=\sqrt[3]{A}](https://forum.fok.nl/lib/mimetex.cgi?x_n%3D%5Csqrt%5B3%5D%7BA%7D)
ook
![x_{n+1}=x_n=\sqrt[3]{A}](https://forum.fok.nl/lib/mimetex.cgi?x_%7Bn%2B1%7D%3Dx_n%3D%5Csqrt%5B3%5D%7BA%7D)
maar hier kom ik niet echt verder mee.
als
Kan iemand me een aanwijzing geven? Ik kan wel aantonen dat als
ook
maar hier kom ik niet echt verder mee.


Ten eerste kun je kijken of A1/3 het enige vaste punt van de substitutie is. Als dat zo is, is het genoeg om na te gaan dat de rij convergeert. Je kan dan bijvoorbeeld nagaan of xn steeds dichterbij A1/3 komt te liggen.


Je hebt hier in feite gewoon de bekende Newton-Raphson iteratie voor de bepaling van het nulpunt van - in dit geval - f(x) = x3 - A, waarbij geldt:quote:Op vrijdag 10 februari 2012 01:19 schreef kutkloon7 het volgende:
Ik moet bewijzen dat
als
Kan iemand me een aanwijzing geven? Ik kan wel aantonen dat als
ook
maar hier kom ik niet echt verder mee.
Je zou eerst moeten aantonen dat je rij {xn} überhaupt convergeert, en dat is nog niet zo eenvoudig (zie hier).


Dat hoeft ook helemaal niet in het algemeen te bewezen worden, maar alleen in dit specifieke geval. Dan wordt het vast makkelijker.quote:Op vrijdag 10 februari 2012 11:31 schreef Riparius het volgende:
[..]
Je hebt hier in feite gewoon de bekende Newton-Raphson iteratie voor de bepaling van het nulpunt van - in dit geval - f(x) = x3 - A, waarbij geldt:
[ afbeelding ]
Je zou eerst moeten aantonen dat je rij {xn} überhaupt convergeert, en dat is nog niet zo eenvoudig (zie hier).


1) Kan elke permutatie van {A,B,C,D} gemaakt worden uit de tranposities (AB), (BC) en (CD)?
Ja, want ik kan de transposities (AC), (AD) en (BD) schrijven als product van de andere drie transposities, en elke permutatie is een product van transposities.
2) Hoeveel vermenigvuldigingen zijn er dan maximaal nodig?
Bij 1) vond ik dat ik (AC) 3 stappen kost om te maken. (BD) ook 3 en (AD) 5.
Van ABCD naar DCBA (of CDAB) gaan kost dan 6 stappen en ik vermoed dat dit het maximale is. Maar hoe bewijs je zoiets?
Ja, want ik kan de transposities (AC), (AD) en (BD) schrijven als product van de andere drie transposities, en elke permutatie is een product van transposities.
2) Hoeveel vermenigvuldigingen zijn er dan maximaal nodig?
Bij 1) vond ik dat ik (AC) 3 stappen kost om te maken. (BD) ook 3 en (AD) 5.
Van ABCD naar DCBA (of CDAB) gaan kost dan 6 stappen en ik vermoed dat dit het maximale is. Maar hoe bewijs je zoiets?


Neem {A,B,C,D} als beginpermutatie. Gegeven een eindpermutatie. Neem de letter die in de eindpermutatie in de uiterst rechter positie terecht moet komen (positie 4). Dit kan in hoogstens 3 stappen. Nu de rechterletter vaststaat, is het probleem gereduceerd tot het volgende:quote:Op zaterdag 11 februari 2012 21:05 schreef Anoonumos het volgende:
1) Kan elke permutatie van {A,B,C,D} gemaakt worden uit de tranposities (AB), (BC) en (CD)?
Ja, want ik kan de transposities (AC), (AD) en (BD) schrijven als product van de andere drie transposities, en elke permutatie is een product van transposities.
2) Hoeveel vermenigvuldigingen zijn er dan maximaal nodig?
Bij 1) vond ik dat ik (AC) 3 stappen kost om te maken. (BD) ook 3 en (AD) 5.
Van ABCD naar DCBA (of CDAB) gaan kost dan 6 stappen en ik vermoed dat dit het maximale is. Maar hoe bewijs je zoiets?
"Hoeveel vermenigvuldigingen zijn er maximaal nodig om van {A,B,C} met de transposities (AB) en (BC) een willekeurige permutatie van {A,B,C} te maken".
Als je het argument op deze manier afmaakt krijg je 3+2+1=6.


Dank. 
Dus voor het geval dat je alleen de transpositie (AB) en 4-cykel (ABCD) mag gebruiken, is het:
4 + 3 + 1 = 7
maximaal 4 stappen om de eerste 2 in volgorde te zetten, en dan nog 3 + 1 om alles om op de goede plaats te zetten (doorschuiven) en eventueel de laatste 2 nog in goede volgorde te zetten.
Dus voor het geval dat je alleen de transpositie (AB) en 4-cykel (ABCD) mag gebruiken, is het:
4 + 3 + 1 = 7
maximaal 4 stappen om de eerste 2 in volgorde te zetten, en dan nog 3 + 1 om alles om op de goede plaats te zetten (doorschuiven) en eventueel de laatste 2 nog in goede volgorde te zetten.


Je geeft nu een bovengrens voor het aantal vermenigvuldigingen.quote:Op zaterdag 11 februari 2012 21:50 schreef thenxero het volgende:
[..]
Neem {A,B,C,D} als beginpermutatie. Gegeven een eindpermutatie. Neem de letter die in de eindpermutatie in de uiterst rechter positie terecht moet komen (positie 4). Dit kan in hoogstens 3 stappen. Nu de rechterletter vaststaat, is het probleem gereduceerd tot het volgende:
"Hoeveel vermenigvuldigingen zijn er maximaal nodig om van {A,B,C} met de transposities (AB) en (BC) een willekeurige permutatie van {A,B,C} te maken".
Als je het argument op deze manier afmaakt krijg je 3+2+1=6.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


De vraagsteller had 6 ook al als ondergrens.quote:Op zaterdag 11 februari 2012 23:15 schreef GlowMouse het volgende:
[..]
Je geeft nu een bovengrens voor het aantal vermenigvuldigingen.


Ahja, al zou dat wel even bewezen moeten worden.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik snap niet echt wat je hier bedoelt. (ABCD) verandert de volgorde van je permutatie niet (?).quote:Op zaterdag 11 februari 2012 23:10 schreef Anoonumos het volgende:
Dank.
Dus voor het geval dat je alleen de transpositie (AB) en 4-cykel (ABCD) mag gebruiken, is het:
4 + 3 + 1 = 7
maximaal 4 stappen om de eerste 2 in volgorde te zetten, en dan nog 3 + 1 om alles om op de goede plaats te zetten (doorschuiven) en eventueel de laatste 2 nog in goede volgorde te zetten.
En daarnaast is 4+3+1 natuurlijk geen 7


Je hebt wel gelijk dat alleen een bewijs gevraagd wordt voor de convergentie van deze specifieke iteratie, maar ook dat is niet echt eenvoudig en in zijn algemeenheid trouwens niet juist. Als we bijvoorbeeld A = 2 kiezen en als startwaarde x0 = -1, dan breekt de iteratie af na x1 = 0 omdat x2 dan ongedefinieerd is. De vragensteller geeft dus onvolledige informatie. Als we echter veronderstellen dat A > 0 en tevens x0 > 0 kiezen dan gaat het wel goed. Het is dan mogelijk te bewijzen dat de rij {xn} in ieder geval vanaf de tweede term x1 monotoon dalend is en tevens begrensd, waaruit volgt dat de rij een limiet heeft. En dan is het niet moeilijk meer te bewijzen dat die limiet inderdaad A1/3 is.quote:Op vrijdag 10 februari 2012 12:52 schreef thenxero het volgende:
[..]
Dat hoeft ook helemaal niet in het algemeen te bewezen worden, maar alleen in dit specifieke geval. Dan wordt het vast makkelijker.


Kan iemand deze voor mij oplossen?
3 √16
---------- =
2 * 4√64
(de 4 is de 4e machtswortel van 64)
3 √16
---------- =
2 * 4√64
(de 4 is de 4e machtswortel van 64)
PSN-ID: SoliD_S


Klik.quote:Op dinsdag 14 februari 2012 15:13 schreef solidslayer het volgende:
Kan iemand deze voor mij oplossen?
3 √16
---------- =
2 * 4√64
(de 4 is de 4e machtswortel van 64)
The biggest argument against democracy is a five minute discussion with the average voter.


Dit artikel gaat alleen over het bestaan van de derdemachtswortel van 2 als reëel getal, en daar schiet je niets mee op voor jouw vraagstuk. Ik denk dat je je vraagstuk erg onderschat, dus ik zal even laten zien hoe ik het zou aanpakken.quote:Op woensdag 15 februari 2012 18:19 schreef kutkloon7 het volgende:
[..]
Bedankt voor de reacties!
Hier staat ook een manier, kwam ik toevallig tegen.
Gegeven is de functie f(x) = x3 - A, waarbij ik A > 0 veronderstel om redenen die ik eerder al heb aangegeven. We willen nu het nulpunt x = A1/3 van deze functie gaan benaderen met de iteratiemethode van Newton-Raphson. Dit houdt in dat we een startwaarde x0 > 0 kiezen en dan een steeds betere benadering van het nulpunt berekenen met de recursieve betrekking:
(1) xn+1 = xn - f(xn)/f'(xn)
Gevraagd wordt nu te bewijzen dat (a) de aldus verkregen rij {xn} convergent is en (b) dat de limiet van deze rij gelijk is aan A1/3.
De methode van Newton-Raphson berust erop dat we, uitgaande van een eerder berekende waarde xn, de vergelijking opstellen van de raaklijn aan de curve van f in het punt (xn;f(xn)) en het snijpunt van de raaklijn met de x-as berekenen. De x-coördinaat van het snijpunt van deze raaklijn met de x-as is dan de nieuwe benadering xn+1. De richtingscoëfficiënt van de raaklijn aan de curve van f in het punt (xn;f(xn)) is f'(xn) en de vergelijking van een rechte lijn met richtingscoëfficiënt m door een punt P(xP;yP) is y - yP = m(x - xP), zodat we voor de vergelijking van de raaklijn krijgen:
(2) y - f(xn) = f'(xn)(x - xn)
Door y = 0 te nemen in (2) vind je x = xn - f(xn)/f'(xn) voor de x-coördinaat van het snijpunt van de raaklijn met de x-as. Deze waarde is dan de nieuwe benadering xn+1, waarmee dus de recursieformule (1) is verklaard.
In ons geval hebben we f(x) = x3 - A en dus f'(x) = 3x2, zodat het recursievoorschrift (1) wordt:
(3) xn+1 = xn - ((xn3 - A)/3xn2)
Hier kunnen we in het rechterlid een factor xn buiten haakjes halen en xn - ((xn3 - A)/3xn2) herschrijven als xn - xn((xn3 - A)/3xn3) = xn + xn((A - xn3)/3xn3) = xn + (1/3)xn((A/xn3 - 1) = xn [1 + (1/3)(A/xn3 -1)], zodat voor (3) ook is te schrijven:
(4) xn+1 = xn [1 + (1/3)(A/xn3 -1)]
En door beide leden van (4) te delen door xn en vervolgens van beide leden 1 af te trekken is (4) ook nog te schrijven als:
(5) xn+1/xn - 1 = (1/3)(A/xn3 - 1)
Uiteraard moet hierbij xn steeds ongelijk aan nul zijn, daar xn+1 anders niet is gedefinieerd en de recursie dan afbreekt.
Zoals ik zal laten zien is het voldoende om een startwaarde x0 > 0 te kiezen om te kunnen garanderen dat xn nooit nul wordt.
We bekijken nu eerst wat er gebeurt met de recursie als xn ≥ A1/3. In dit geval is (xn3 - A) ≥ 0 en dus ook ((xn3 - A)/3xn2) ≥ 0, zodat uit (3) volgt dat dan xn+1 ≤ xn. Dus: als xn ≥ A1/3 dan is xn+1 ≤ xn.
Maar, aan de hand van (4) kunnen we nog iets anders concluderen. Uit A > 0 en xn > 0 volgt uiteraard A/xn3 > 0 en dus ook A/xn3 - 1 > -1 en dus a fortiori (1/3)(A/xn3 -1) > -1. En dus volgt uit (4) op grond van de ongelijkheid van Bernoulli dat:
(6) xn+13 = xn3[1 + (1/3)(A/xn3 -1)]3 ≥ xn3(1 + A/xn3 - 1) = A
Dus: als xn > 0 dan geldt xn+13 ≥ A en derhalve xn+1 ≥ A1/3. Dit impliceert dat voor elke startwaarde x0 > 0 geldt dat x1 ≥ A1/3 en daarmee xn ≥ A1/3 voor elke n > 0. Maar we hadden net al gezien dat voor elke xn ≥ A1/3 ook geldt xn+1 ≤ xn. En dus vinden we dat ongeacht de gekozen startwaarde x0 > 0 geldt:
(7) A1/3 ≤ xn+1 ≤ xn voor elke n > 0
We zien dus dat de rij {xn} in ieder geval vanaf de tweede term x1 monotoon dalend is én dat deze rij een ondergrens A1/3 heeft. En een monotoon dalende rij met een ondergrens is convergent.
We hebben nu bewezen dat limn→∞ xn bestaat, maar daarmee zijn we er nog niet. We moeten nu nog aantonen dat deze limiet inderdaad gelijk is aan A1/3. Laten we deze limiet L noemen, dus:
(8) limn→∞ xn = L
Het is evident dat L ≥ A1/3 moet zijn. Immers, als L < A1/3 zou zijn, dan zou vanaf een zekere n moeten gelden xn < A1/3 en dat is niet zo, want we hebben gezien dat xn ≥ A1/3 voor elke n > 0. Aangezien L > 0 en uiteraard limn→∞ xn+1 = limn→∞ xn = L volgt uit (8) dat ook geldt:
(9) limn→∞ (xn+1/xn - 1) = 0
En op grond van (5) moet dus ook gelden:
(10) limn→∞ (A/xn3 - 1) = 0
Maar dit impliceert dat:
(11) limn→∞ xn3 = A
Uit (8) volgt echter dat:
(12) limn→∞ xn3 = L3
Op grond van (11) en (12) hebben we L3 = A en dus inderdaad:
(13) L = A1/3
QED
[ Bericht 0% gewijzigd door Riparius op 17-02-2012 22:13:05 ]


Ik wil deze limiet berekenen:
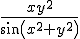
als (x,y) naar (0,0) gaat.
Alleen weet ik niet hoe ik die sinus kan wegwerken. Ik dacht aan een taylorreeks, maar dat hebben we nog niet gehad met twee variabelen. Ik krijg de breuk ook niet kleiner gepraat dan iets zonder sinus.
Heeft iemand een tip?
als (x,y) naar (0,0) gaat.
Alleen weet ik niet hoe ik die sinus kan wegwerken. Ik dacht aan een taylorreeks, maar dat hebben we nog niet gehad met twee variabelen. Ik krijg de breuk ook niet kleiner gepraat dan iets zonder sinus.
Heeft iemand een tip?


Beetje creatief zijn. Bedenk datquote:Op vrijdag 17 februari 2012 22:17 schreef Anoonumos het volgende:
Ik wil deze limiet berekenen:
als (x,y) naar (0,0) gaat.
Alleen weet ik niet hoe ik die sinus kan wegwerken. Ik dacht aan een taylorreeks, maar dat hebben we nog niet gehad met twee variabelen. Ik krijg de breuk ook niet kleiner gepraat dan iets zonder sinus.
Heeft iemand een tip?
(1) limt→0 sin(t)/t = limt→0 t/sin(t) = 1
Dus geldt ook:
(2) lim(x;y)→(0;0) (x2 + y2)/sin(x2 + y2) = 1
Je kunt (xy2)/sin(x2 + y2) herschrijven als het product:
(3) ((x2 + y2)/sin(x2 + y2))∙((xy2)/(x2 + y2))
De limiet van de eerste factor voor (x;y) → (0;0) ken je al, die is 1. Hiermee heb je het probleem herleid tot de bepaling van de limiet van (xy2)/(x2 + y2) voor (x;y) → (0;0). Ga over op poolcoördinaten om aan te tonen dat geldt:
(4) | (xy2)/(x2 + y2) | < √(x2 + y2) voor (x;y) ≠ (0;0)
De limiet van de tweede factor in (3) voor (x;y) → (0;0) is dus 0, zodat de limiet van (3) voor (x;y) → (0;0) ook 0 is. Ergo:
(5) lim(x;y)→(0;0) (xy2)/(sin(x2 + y2)) = 0
[ Bericht 0% gewijzigd door Riparius op 18-02-2012 00:10:38 ]


.
[ Bericht 99% gewijzigd door M.rak op 19-02-2012 16:11:16 ]
[ Bericht 99% gewijzigd door M.rak op 19-02-2012 16:11:16 ]
The biggest argument against democracy is a five minute discussion with the average voter.