[Bèta wiskunde] Huiswerk- en vragentopic

vrijdag 3 februari 2012 @ 12:22:13 #176

GlowMouse

l'état, c'est moi

n/m

[ Bericht 73% gewijzigd door GlowMouse op 03-02-2012 12:39:14 ]

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

vrijdag 3 februari 2012 @ 12:27:23 #177

123hopsaflops

quote:
Op vrijdag 3 februari 2012 12:22 schreef GlowMouse het volgende:
Is y afhankelijk van t?
Rare notatie van een interval.
Als je onderscheid maakt tussen y>=0 en y<0 dan is het toch wel te doen? Alleen opletten bij y=0 wanneer 0<alpha<=1.

verbeterd

www.wiskunde.tk

zondag 5 februari 2012 @ 22:18:42 #178

Anoonumos

Wat gebeurt er met je meetfout als je de meting een aantal keer herhaalt en dan het gemiddelde neemt? Bijvoorbeeld als ik een meetfout van 0,5 cm bij één meting heb en de meting 10x doe en dan het gemiddelde neem.

zondag 5 februari 2012 @ 22:20:09 #179

GlowMouse

l'état, c'est moi

Is de meetfout systematisch of willekeurig? Is die altijd precies 5mm?

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

zondag 5 februari 2012 @ 22:34:25 #180

Anoonumos

Willekeurig en altijd 5mm.

zondag 5 februari 2012 @ 23:19:47 #181

twaalf

Nou ja, je zit erboven of eronder, dus je krijgt iets binomiaals denk ik, 10 trekkingen.

zondag 5 februari 2012 @ 23:26:30 #182

GlowMouse

l'état, c'est moi

quote:
Op zondag 5 februari 2012 23:19 schreef twaalf het volgende:
Nou ja, je zit erboven of eronder, dus je krijgt iets binomiaals denk ik, 10 trekkingen.

Mits de meetfouten onafhankelijk zijn.

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

donderdag 9 februari 2012 @ 13:43:24 #183

bezemsteeltaart

Laat A en B 2x2 matrices zijn met de determinanten |A|=4 en |B|=7

ik weet dat |A|+|B| niet gelijk is aan |A+B| maar wat zijn de verschillen dan?

Is |A|+|B|=11 of is |A+B|=11??

Is |A+B| dan eerst de A+B matrices bij elkaar optellen en daar de determinant van ofzo?? Ik heb geen idee..

donderdag 9 februari 2012 @ 13:52:58 #184

GlowMouse

l'état, c'est moi

quote:
Op donderdag 9 februari 2012 13:43 schreef bezemsteeltaart het volgende:
Is |A+B| dan eerst de A+B matrices bij elkaar optellen en daar de determinant van?

precies, dat staat er

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

donderdag 9 februari 2012 @ 17:28:28 #185

123hopsaflops

quote:
Op donderdag 9 februari 2012 13:43 schreef bezemsteeltaart het volgende:
Laat A en B 2x2 matrices zijn met de determinanten |A|=4 en |B|=7

ik weet dat |A|+|B| niet gelijk is aan |A+B| maar wat zijn de verschillen dan?

Is |A|+|B|=11 of is |A+B|=11??

Is |A+B| dan eerst de A+B matrices bij elkaar optellen en daar de determinant van ofzo?? Ik heb geen idee..

ik zou twee voorbeeldmatrices maken en het dan allebei uitproberen

let er op dat je geen 0 invoert op x_12 en x_21

(met die laatste tip zou je al moeten zien waar het mis gaat)

www.wiskunde.tk

vrijdag 10 februari 2012 @ 01:19:07 #186

kutkloon7

Ik moet bewijzen dat
$\lim_{n \to \infty}{x_n}=\sqrt[3]{A}$

als

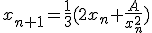
$x_{n+1}=\frac{1}{3}(2x_n+\frac{A}{x_n^2})$

Kan iemand me een aanwijzing geven? Ik kan wel aantonen dat als
$x_n=\sqrt[3]{A}$

ook

$x_{n+1}=x_n=\sqrt[3]{A}$

maar hier kom ik niet echt verder mee.

vrijdag 10 februari 2012 @ 11:20:03 #187

thabit

Ten eerste kun je kijken of A^1/3 het enige vaste punt van de substitutie is. Als dat zo is, is het genoeg om na te gaan dat de rij convergeert. Je kan dan bijvoorbeeld nagaan of x_n steeds dichterbij A^1/3 komt te liggen.

vrijdag 10 februari 2012 @ 11:31:48 #188

Riparius

quote:
Op vrijdag 10 februari 2012 01:19 schreef kutkloon7 het volgende:
Ik moet bewijzen dat
$\lim_{n \to \infty}{x_n}=\sqrt[3]{A}$

als

$x_{n+1}=\frac{1}{3}(2x_n+\frac{A}{x_n^2})$

Kan iemand me een aanwijzing geven? Ik kan wel aantonen dat als
$x_n=\sqrt[3]{A}$

ook

$x_{n+1}=x_n=\sqrt[3]{A}$

maar hier kom ik niet echt verder mee.

Je hebt hier in feite gewoon de bekende Newton-Raphson iteratie voor de bepaling van het nulpunt van - in dit geval - f(x) = x³ - A, waarbij geldt:

Je zou eerst moeten aantonen dat je rij {x_n} überhaupt convergeert, en dat is nog niet zo eenvoudig (zie hier).

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

vrijdag 10 februari 2012 @ 12:52:16 #189

thenxero

quote:
Op vrijdag 10 februari 2012 11:31 schreef Riparius het volgende:

[..]

Je hebt hier in feite gewoon de bekende Newton-Raphson iteratie voor de bepaling van het nulpunt van - in dit geval - f(x) = x³ - A, waarbij geldt:

[ afbeelding ]

Je zou eerst moeten aantonen dat je rij {x_n} überhaupt convergeert, en dat is nog niet zo eenvoudig (zie hier).

Dat hoeft ook helemaal niet in het algemeen te bewezen worden, maar alleen in dit specifieke geval. Dan wordt het vast makkelijker.

zaterdag 11 februari 2012 @ 21:05:31 #190

Anoonumos

1) Kan elke permutatie van {A,B,C,D} gemaakt worden uit de tranposities (AB), (BC) en (CD)?
Ja, want ik kan de transposities (AC), (AD) en (BD) schrijven als product van de andere drie transposities, en elke permutatie is een product van transposities.

2) Hoeveel vermenigvuldigingen zijn er dan maximaal nodig?

Bij 1) vond ik dat ik (AC) 3 stappen kost om te maken. (BD) ook 3 en (AD) 5.
Van ABCD naar DCBA (of CDAB) gaan kost dan 6 stappen en ik vermoed dat dit het maximale is. Maar hoe bewijs je zoiets?

zaterdag 11 februari 2012 @ 21:50:30 #191

thenxero

quote:
Op zaterdag 11 februari 2012 21:05 schreef Anoonumos het volgende:
1) Kan elke permutatie van {A,B,C,D} gemaakt worden uit de tranposities (AB), (BC) en (CD)?
Ja, want ik kan de transposities (AC), (AD) en (BD) schrijven als product van de andere drie transposities, en elke permutatie is een product van transposities.

2) Hoeveel vermenigvuldigingen zijn er dan maximaal nodig?

Bij 1) vond ik dat ik (AC) 3 stappen kost om te maken. (BD) ook 3 en (AD) 5.
Van ABCD naar DCBA (of CDAB) gaan kost dan 6 stappen en ik vermoed dat dit het maximale is. Maar hoe bewijs je zoiets?

Neem {A,B,C,D} als beginpermutatie. Gegeven een eindpermutatie. Neem de letter die in de eindpermutatie in de uiterst rechter positie terecht moet komen (positie 4). Dit kan in hoogstens 3 stappen. Nu de rechterletter vaststaat, is het probleem gereduceerd tot het volgende:
"Hoeveel vermenigvuldigingen zijn er maximaal nodig om van {A,B,C} met de transposities (AB) en (BC) een willekeurige permutatie van {A,B,C} te maken".

Als je het argument op deze manier afmaakt krijg je 3+2+1=6.

zaterdag 11 februari 2012 @ 23:10:17 #192

Anoonumos

Dank.

Dus voor het geval dat je alleen de transpositie (AB) en 4-cykel (ABCD) mag gebruiken, is het:

4 + 3 + 1 = 7
maximaal 4 stappen om de eerste 2 in volgorde te zetten, en dan nog 3 + 1 om alles om op de goede plaats te zetten (doorschuiven) en eventueel de laatste 2 nog in goede volgorde te zetten.

zaterdag 11 februari 2012 @ 23:15:40 #193

GlowMouse

l'état, c'est moi

quote:
Op zaterdag 11 februari 2012 21:50 schreef thenxero het volgende:

[..]

Neem {A,B,C,D} als beginpermutatie. Gegeven een eindpermutatie. Neem de letter die in de eindpermutatie in de uiterst rechter positie terecht moet komen (positie 4). Dit kan in hoogstens 3 stappen. Nu de rechterletter vaststaat, is het probleem gereduceerd tot het volgende:
"Hoeveel vermenigvuldigingen zijn er maximaal nodig om van {A,B,C} met de transposities (AB) en (BC) een willekeurige permutatie van {A,B,C} te maken".

Als je het argument op deze manier afmaakt krijg je 3+2+1=6.

Je geeft nu een bovengrens voor het aantal vermenigvuldigingen.

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

zaterdag 11 februari 2012 @ 23:28:23 #194

thenxero

quote:
Op zaterdag 11 februari 2012 23:15 schreef GlowMouse het volgende:

[..]

Je geeft nu een bovengrens voor het aantal vermenigvuldigingen.

De vraagsteller had 6 ook al als ondergrens.

zaterdag 11 februari 2012 @ 23:30:21 #195

GlowMouse

l'état, c'est moi

Ahja, al zou dat wel even bewezen moeten worden.

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

zaterdag 11 februari 2012 @ 23:34:13 #196

thenxero

quote:
Op zaterdag 11 februari 2012 23:10 schreef Anoonumos het volgende:
Dank.
Dus voor het geval dat je alleen de transpositie (AB) en 4-cykel (ABCD) mag gebruiken, is het:

4 + 3 + 1 = 7
maximaal 4 stappen om de eerste 2 in volgorde te zetten, en dan nog 3 + 1 om alles om op de goede plaats te zetten (doorschuiven) en eventueel de laatste 2 nog in goede volgorde te zetten.

Ik snap niet echt wat je hier bedoelt. (ABCD) verandert de volgorde van je permutatie niet (?).

En daarnaast is 4+3+1 natuurlijk geen 7

zondag 12 februari 2012 @ 17:19:09 #197

Riparius

quote:
Op vrijdag 10 februari 2012 12:52 schreef thenxero het volgende:

[..]

Dat hoeft ook helemaal niet in het algemeen te bewezen worden, maar alleen in dit specifieke geval. Dan wordt het vast makkelijker.

Je hebt wel gelijk dat alleen een bewijs gevraagd wordt voor de convergentie van deze specifieke iteratie, maar ook dat is niet echt eenvoudig en in zijn algemeenheid trouwens niet juist. Als we bijvoorbeeld A = 2 kiezen en als startwaarde x₀ = -1, dan breekt de iteratie af na x₁ = 0 omdat x₂ dan ongedefinieerd is. De vragensteller geeft dus onvolledige informatie. Als we echter veronderstellen dat A > 0 en tevens x₀ > 0 kiezen dan gaat het wel goed. Het is dan mogelijk te bewijzen dat de rij {x_n} in ieder geval vanaf de tweede term x₁ monotoon dalend is en tevens begrensd, waaruit volgt dat de rij een limiet heeft. En dan is het niet moeilijk meer te bewijzen dat die limiet inderdaad A^1/3 is.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

dinsdag 14 februari 2012 @ 15:13:44 #198

solidslayer

to much is never enough

Kan iemand deze voor mij oplossen?

3 √16
---------- =
2 * 4√64

(de 4 is de 4e machtswortel van 64)

PSN-ID: SoliD_S

dinsdag 14 februari 2012 @ 15:23:41 #199

M.rak

quote:
Op dinsdag 14 februari 2012 15:13 schreef solidslayer het volgende:
Kan iemand deze voor mij oplossen?

3 √16
---------- =
2 * 4√64

(de 4 is de 4e machtswortel van 64)

Klik.

The biggest argument against democracy is a five minute discussion with the average voter.

Moderator / Redactie Sport / Devops dinsdag 14 februari 2012 @ 15:34:27 #200

zoem

zoemt

Herschrijven naar machten met basisgetal 4 en de regel $\sqrt[n]{a^m}=a^{m/n}$ gebruiken:

1. $\sqrt{16}=4$
2. $\sqrt[4]{64}=\sqrt[4]{4^3}=4^{3/4}$

Dus: $\frac{4}{4^{3/4}}=4^{1/4}(=\sqrt[4]{4})$

Nu 3/2 ervoor en klaar.

Forum Opties
Forumhop:
Hop naar:	(afkorting, bv 'KLB')

» school, studie en onderwijs

» school, studie en onderwijs