SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Dit artikel gaat alleen over het bestaan van de derdemachtswortel van 2 als reëel getal, en daar schiet je niets mee op voor jouw vraagstuk. Ik denk dat je je vraagstuk erg onderschat, dus ik zal even laten zien hoe ik het zou aanpakken.quote:Op woensdag 15 februari 2012 18:19 schreef kutkloon7 het volgende:
[..]
Bedankt voor de reacties!
Hier staat ook een manier, kwam ik toevallig tegen.
Gegeven is de functie f(x) = x3 - A, waarbij ik A > 0 veronderstel om redenen die ik eerder al heb aangegeven. We willen nu het nulpunt x = A1/3 van deze functie gaan benaderen met de iteratiemethode van Newton-Raphson. Dit houdt in dat we een startwaarde x0 > 0 kiezen en dan een steeds betere benadering van het nulpunt berekenen met de recursieve betrekking:
(1) xn+1 = xn - f(xn)/f'(xn)
Gevraagd wordt nu te bewijzen dat (a) de aldus verkregen rij {xn} convergent is en (b) dat de limiet van deze rij gelijk is aan A1/3.
De methode van Newton-Raphson berust erop dat we, uitgaande van een eerder berekende waarde xn, de vergelijking opstellen van de raaklijn aan de curve van f in het punt (xn;f(xn)) en het snijpunt van de raaklijn met de x-as berekenen. De x-coördinaat van het snijpunt van deze raaklijn met de x-as is dan de nieuwe benadering xn+1. De richtingscoëfficiënt van de raaklijn aan de curve van f in het punt (xn;f(xn)) is f'(xn) en de vergelijking van een rechte lijn met richtingscoëfficiënt m door een punt P(xP;yP) is y - yP = m(x - xP), zodat we voor de vergelijking van de raaklijn krijgen:
(2) y - f(xn) = f'(xn)(x - xn)
Door y = 0 te nemen in (2) vind je x = xn - f(xn)/f'(xn) voor de x-coördinaat van het snijpunt van de raaklijn met de x-as. Deze waarde is dan de nieuwe benadering xn+1, waarmee dus de recursieformule (1) is verklaard.
In ons geval hebben we f(x) = x3 - A en dus f'(x) = 3x2, zodat het recursievoorschrift (1) wordt:
(3) xn+1 = xn - ((xn3 - A)/3xn2)
Hier kunnen we in het rechterlid een factor xn buiten haakjes halen en xn - ((xn3 - A)/3xn2) herschrijven als xn - xn((xn3 - A)/3xn3) = xn + xn((A - xn3)/3xn3) = xn + (1/3)xn((A/xn3 - 1) = xn [1 + (1/3)(A/xn3 -1)], zodat voor (3) ook is te schrijven:
(4) xn+1 = xn [1 + (1/3)(A/xn3 -1)]
En door beide leden van (4) te delen door xn en vervolgens van beide leden 1 af te trekken is (4) ook nog te schrijven als:
(5) xn+1/xn - 1 = (1/3)(A/xn3 - 1)
Uiteraard moet hierbij xn steeds ongelijk aan nul zijn, daar xn+1 anders niet is gedefinieerd en de recursie dan afbreekt.
Zoals ik zal laten zien is het voldoende om een startwaarde x0 > 0 te kiezen om te kunnen garanderen dat xn nooit nul wordt.
We bekijken nu eerst wat er gebeurt met de recursie als xn ≥ A1/3. In dit geval is (xn3 - A) ≥ 0 en dus ook ((xn3 - A)/3xn2) ≥ 0, zodat uit (3) volgt dat dan xn+1 ≤ xn. Dus: als xn ≥ A1/3 dan is xn+1 ≤ xn.
Maar, aan de hand van (4) kunnen we nog iets anders concluderen. Uit A > 0 en xn > 0 volgt uiteraard A/xn3 > 0 en dus ook A/xn3 - 1 > -1 en dus a fortiori (1/3)(A/xn3 -1) > -1. En dus volgt uit (4) op grond van de ongelijkheid van Bernoulli dat:
(6) xn+13 = xn3[1 + (1/3)(A/xn3 -1)]3 ≥ xn3(1 + A/xn3 - 1) = A
Dus: als xn > 0 dan geldt xn+13 ≥ A en derhalve xn+1 ≥ A1/3. Dit impliceert dat voor elke startwaarde x0 > 0 geldt dat x1 ≥ A1/3 en daarmee xn ≥ A1/3 voor elke n > 0. Maar we hadden net al gezien dat voor elke xn ≥ A1/3 ook geldt xn+1 ≤ xn. En dus vinden we dat ongeacht de gekozen startwaarde x0 > 0 geldt:
(7) A1/3 ≤ xn+1 ≤ xn voor elke n > 0
We zien dus dat de rij {xn} in ieder geval vanaf de tweede term x1 monotoon dalend is én dat deze rij een ondergrens A1/3 heeft. En een monotoon dalende rij met een ondergrens is convergent.
We hebben nu bewezen dat limn→∞ xn bestaat, maar daarmee zijn we er nog niet. We moeten nu nog aantonen dat deze limiet inderdaad gelijk is aan A1/3. Laten we deze limiet L noemen, dus:
(8) limn→∞ xn = L
Het is evident dat L ≥ A1/3 moet zijn. Immers, als L < A1/3 zou zijn, dan zou vanaf een zekere n moeten gelden xn < A1/3 en dat is niet zo, want we hebben gezien dat xn ≥ A1/3 voor elke n > 0. Aangezien L > 0 en uiteraard limn→∞ xn+1 = limn→∞ xn = L volgt uit (8) dat ook geldt:
(9) limn→∞ (xn+1/xn - 1) = 0
En op grond van (5) moet dus ook gelden:
(10) limn→∞ (A/xn3 - 1) = 0
Maar dit impliceert dat:
(11) limn→∞ xn3 = A
Uit (8) volgt echter dat:
(12) limn→∞ xn3 = L3
Op grond van (11) en (12) hebben we L3 = A en dus inderdaad:
(13) L = A1/3
QED
[ Bericht 0% gewijzigd door Riparius op 17-02-2012 22:13:05 ]
Ik wil deze limiet berekenen:
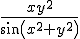
als (x,y) naar (0,0) gaat.
Alleen weet ik niet hoe ik die sinus kan wegwerken. Ik dacht aan een taylorreeks, maar dat hebben we nog niet gehad met twee variabelen. Ik krijg de breuk ook niet kleiner gepraat dan iets zonder sinus.
Heeft iemand een tip?
als (x,y) naar (0,0) gaat.
Alleen weet ik niet hoe ik die sinus kan wegwerken. Ik dacht aan een taylorreeks, maar dat hebben we nog niet gehad met twee variabelen. Ik krijg de breuk ook niet kleiner gepraat dan iets zonder sinus.
Heeft iemand een tip?
Beetje creatief zijn. Bedenk datquote:Op vrijdag 17 februari 2012 22:17 schreef Anoonumos het volgende:
Ik wil deze limiet berekenen:
als (x,y) naar (0,0) gaat.
Alleen weet ik niet hoe ik die sinus kan wegwerken. Ik dacht aan een taylorreeks, maar dat hebben we nog niet gehad met twee variabelen. Ik krijg de breuk ook niet kleiner gepraat dan iets zonder sinus.
Heeft iemand een tip?
(1) limt→0 sin(t)/t = limt→0 t/sin(t) = 1
Dus geldt ook:
(2) lim(x;y)→(0;0) (x2 + y2)/sin(x2 + y2) = 1
Je kunt (xy2)/sin(x2 + y2) herschrijven als het product:
(3) ((x2 + y2)/sin(x2 + y2))∙((xy2)/(x2 + y2))
De limiet van de eerste factor voor (x;y) → (0;0) ken je al, die is 1. Hiermee heb je het probleem herleid tot de bepaling van de limiet van (xy2)/(x2 + y2) voor (x;y) → (0;0). Ga over op poolcoördinaten om aan te tonen dat geldt:
(4) | (xy2)/(x2 + y2) | < √(x2 + y2) voor (x;y) ≠ (0;0)
De limiet van de tweede factor in (3) voor (x;y) → (0;0) is dus 0, zodat de limiet van (3) voor (x;y) → (0;0) ook 0 is. Ergo:
(5) lim(x;y)→(0;0) (xy2)/(sin(x2 + y2)) = 0
[ Bericht 0% gewijzigd door Riparius op 18-02-2012 00:10:38 ]
.
[ Bericht 99% gewijzigd door M.rak op 19-02-2012 16:11:16 ]
[ Bericht 99% gewijzigd door M.rak op 19-02-2012 16:11:16 ]
The biggest argument against democracy is a five minute discussion with the average voter.
waarbij jequote:
ook op kunt schrijven als:
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Kloptj, de uiteindelijke integraal wordt dusquote:Op zondag 19 februari 2012 16:18 schreef GlowMouse het volgende:
[..]
waarbij je
ook op kunt schrijven als:
The biggest argument against democracy is a five minute discussion with the average voter.
ik zag het wel, met je ninja-editquote:
[..]
Kloptj, de uiteindelijke integraal wordt dus
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Psst!quote:Op zondag 19 februari 2012 16:20 schreef GlowMouse het volgende:
[..]
ik zag het wel, met je ninja-edit
The biggest argument against democracy is a five minute discussion with the average voter.
waar gaat die initiele +1 dan heen van:quote:
[..]
waarbij je
ook op kunt schrijven als:
Er is geen +1.quote:
[..]
waar gaat die initiele +1 dan heen van:?
Je moet (x+3) buiten haakjes halen, dan heb je er x²+1 van en je hebt er -1 van, dus x² totaal.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
psst, die is nog steeds fout hoor; je vergat nl. de absoluutstrepen om de term v/d logaritmequote:
[..]
Klopt, de uiteindelijke integraal wordt dus
Ach, zolang er geen verdere randvoorwaarden vermeldt staan lig ik daar niet wakker van 
. Foutieve domeinrestrictie daarintegen 
...
. Foutieve domeinrestrictie daarintegen ...
wat is de nederlandse naam voor equation ookalweer? ben het ff helemaal kwijt 
Winnaar KLB verkiezingen 2012.
Vergelijking is denk ik wat het meest in de buurt komt. Google translate?quote:Op dinsdag 21 februari 2012 20:05 schreef gogosweden het volgende:
wat is de nederlandse naam voor equation ookalweer? ben het ff helemaal kwijt
het klonk toch niet helemaal goed dus daarom vroeg ik het hier voor de zekerheid naquote:
[..]
Vergelijking is denk ik wat het meest in de buurt komt. Google translate?
Winnaar KLB verkiezingen 2012.
