SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Je hebt door de CLT iets staan met Y_n op de plek waar straks f(x_n) komt te staan. Je wilt daar de momentenschatter theta_MM hebben staan. Een logische keuze is dan:
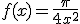
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


klopt
ik kan 't niet controleren verder zonder i te weten, maar het lijkt allemaal goed te gaan
ik kan 't niet controleren verder zonder i te weten, maar het lijkt allemaal goed te gaan
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Docent heeft het antwoord bijgevoegd:
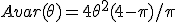
En op deze manier kom ik daar niet op uit, in ieder geval bedankt voor je hulp steeds!
En op deze manier kom ik daar niet op uit, in ieder geval bedankt voor je hulp steeds!


Daar kom ik wel op uit. Wat krijg je voor f'(c)?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


En als ik dan verder ga kom ik beetje vast te zitten. Als ik labda 1 wegwerk en dan omschrijf naar iets voor labda 2 en dat weer substitueer kom ik op iets compleet nutteloos (bv x2x3=x2x3).
Aan 1e restrictie kan ik zien dat bv. 2 xi positief zijn en 1 xi negatief is.
Mijn ''intuitie'' zegt dat het min te vinden is voor x1=x2=-0.5x3, maar iemand suggestie waarom ik dit hieruit kan afleiden?
Beneath the gold, bitter steel


Om te beginnen zou ik die Lagrange functie schrijven als Λ(x1,x2,x3,λ1,λ2), je hebt tenslotte vijf variabelen, en dus vijf partiële afgeleiden die nul moeten zijn (de drie partiële afgeleiden naar x1,x2 en x3 die je geeft en de twee partiële afgeleiden naar λ1 en λ2 die je voorwaarden leveren). We hebben zo dus een stelsel van vijf vergelijkingen met vijf onbekenden. Maar nu zie je gemakkelijk dat een permutatie van x1, x2 en x3 in hetzelfde stelsel vergelijkingen resulteert, zodat we ook zonder rekenwerk al kunnen vermoeden dat er 3∙2∙1 = 6 oplossingen zijn (waarvan drie een minimum en drie een maximum opleveren). Een snelle controle met WolframAlpha leert dat dat klopt (minima en maxima).quote:Op donderdag 3 november 2011 21:51 schreef Fingon het volgende:
[ afbeelding ]
En als ik dan verder ga kom ik beetje vast te zitten. Als ik labda 1 wegwerk en dan omschrijf naar iets voor labda 2 en dat weer substitueer kom ik op iets compleet nutteloos (bv x2x3=x2x3).
Aan 1e restrictie kan ik zien dat bv. 2 xi positief zijn en 1 xi negatief is.
Mijn ''intuitie'' zegt dat het min te vinden is voor x1=x2=-0.5x3, maar iemand suggestie waarom ik dit hieruit kan afleiden?
Maar goed, je wil dit uiteraard met pen en papier verifiëren. Uit ∂Λ/∂x1 = ∂Λ/∂x2 = 0 volgt dat het verschil van deze afgeleiden ook nul moet zijn en dat levert:
(x2 - x1)x3 - 2λ2(x1 - x2) = 0,
waarvoor we ook kunnen schrijven:
(x2 - x1)(x3 + 2λ2) = 0
Aan deze voorwaarde is voldaan als x2 = x1 of als x3 = -2λ2. Elk van deze beide substituties afzonderlijk resulteert erin dat je nog maar vier vergelijkingen met vier onbekenden overhoudt, omdat er dan twee vergelijkingen samenvallen (ga dit na). Rekenen we even verder met x2 = x1 dan volgt door substitutie daarvan in je beide voorwaarden gemakkelijk dat x12 = x22 = 1/6. Nu kun je het verder zelf wel uitwerken. Vanwege het feit dat elke permutatie van x1, x2 en x3 ook voldoet komt het erop neer dat het product x1x2x3 een minimum -(1/3)∙√(1/6) bereikt onder de gegeven voorwaarden als twee van de drie variabelen gelijk zijn aan √(1/6) en de derde gelijk is aan -2√(1/6) = -√(2/3).


Idd, toevallig kwam het excelvoorbeeld wat ik had berekend afgerond op hetzelfde antwoord uit.quote:
Hoe kan ik het numeriek doen?


Ben er uiteindelijk wel uitgekomen, dankjewel!quote:Op donderdag 3 november 2011 21:48 schreef GlowMouse het volgende:
Daar kom ik wel op uit. Wat krijg je voor f'(c)?


Zij X de verzameling van functies van de natuurlijke getallen naar zichzelf. Zij A een deelverzameling van X, met de eigenschap dat er voor iedere functie f: N -> N een functie g in A bestaat, zodanig dat er voor ieder natuurlijk getal n een getal 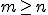 bestaat, zodanig dat f(m)<g(m).
bestaat, zodanig dat f(m)<g(m).
Nu wil ik bewijzen dat A niet aftelbaar is.
Het lukt me niet om te bewijzen dat A niet aftelbaar moet zijn, maar het is wel duidelijk dat A niet eindig mag zijn. Stel A is eindig. Definieer de functie
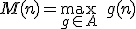 .
.
Deze functie is goed gedefinieerd omdat A eindig is. Beschouw nu de functie M'(n) = M(n)+1. Voor iedere n in N geldt dan M'(n) > M(n), en dus ook M'(n) > g(n) voor alle g in A. Dus een eindige A kan niet aan de gewenste eigenschap voldoen.
Volgens mij mis ik iets eenvoudigs maar het lukt me niet om een dergelijk bewijs te voeren voor aftelbare verzamelingen. Iemand een idee? Het keuze-axioma mogen we aannemen, mocht die van pas komen.
Nu wil ik bewijzen dat A niet aftelbaar is.
Het lukt me niet om te bewijzen dat A niet aftelbaar moet zijn, maar het is wel duidelijk dat A niet eindig mag zijn. Stel A is eindig. Definieer de functie
Deze functie is goed gedefinieerd omdat A eindig is. Beschouw nu de functie M'(n) = M(n)+1. Voor iedere n in N geldt dan M'(n) > M(n), en dus ook M'(n) > g(n) voor alle g in A. Dus een eindige A kan niet aan de gewenste eigenschap voldoen.
Volgens mij mis ik iets eenvoudigs maar het lukt me niet om een dergelijk bewijs te voeren voor aftelbare verzamelingen. Iemand een idee? Het keuze-axioma mogen we aannemen, mocht die van pas komen.


Stel A is aftelbaar. Dan kunnen we dus voor elke n in N een gn in A kiezen. Kies nu f(m) = maxn<=mgn(m). Er is een gn in A zdd er oneindig veel m zijn met f(m) < gn(m), per definitie van A. Maar als m >= n, dan geldt, per definitie van f, dat f(m) >= gn(m); tegenspraak.


Bedankt! ik zat toch in de goede richting alleen ik kwam niet op die functie van f(m), ook al is die bijna hetzelfde als wat ik gebruikte bij M(n).


'Laat a een natuurlijk getal zijn, en [cn,...,c0] de tientallige notatie van a zijn.
Bewijs dat a en cn+...+c0 dezelfde rest geven met deling door 9.'
Ik zie werkelijk niet in hoe ik dit moet bewijzen, heeft iemand een hint?
Bewijs dat a en cn+...+c0 dezelfde rest geven met deling door 9.'
Ik zie werkelijk niet in hoe ik dit moet bewijzen, heeft iemand een hint?


Laten we even modulo 9 gaan denken.
0 = 9
1 = 10
2 = 11
3 = 12
4 = 13
etc
Merk op dat de som van de cijfers links steeds hetzelfde is als de som van de cijfers rechts, behalve bij 0=9.
Dus als het getal bijvoorbeeld eindigt op 23, dan kan je er rustig 9 vanafhalen en dan krijg je 14. Nog steeds geldt dan 2+3 = 1+4 dus cn+...+c0 blijft hetzelfde.
0 = 9
1 = 10
2 = 11
3 = 12
4 = 13
etc
Merk op dat de som van de cijfers links steeds hetzelfde is als de som van de cijfers rechts, behalve bij 0=9.
Dus als het getal bijvoorbeeld eindigt op 23, dan kan je er rustig 9 vanafhalen en dan krijg je 14. Nog steeds geldt dan 2+3 = 1+4 dus cn+...+c0 blijft hetzelfde.


Ik weet niet zeker of dit een bewijs is, of juist iets wat uit de stelling die ik moet bewijzen volgt.quote:Op zaterdag 5 november 2011 13:01 schreef thenxero het volgende:
Laten we even modulo 9 gaan denken.
0 = 9
1 = 10
2 = 11
3 = 12
4 = 13
etc
Merk op dat de som van de cijfers links steeds hetzelfde is als de som van de cijfers rechts, behalve bij 0=9.
Dus als het getal bijvoorbeeld eindigt op 23, dan kan je er rustig 9 vanafhalen en dan krijg je 14. Nog steeds geldt dan 2+3 = 1+4 dus cn+...+c0 blijft hetzelfde.
En ik weet niet zeker in hoevere ik modulo mag/kan rekenen en hoe dit samenhangt met wat ik nu ben het behandelen, dus ik zal er nog eens naar kijken.
Bedankt in ieder geval.


Het bewijst nog niks; het was een hint, daar vroeg je immers om. Ik zal het iets verder uitleggen.quote:Op zaterdag 5 november 2011 19:41 schreef Siddartha het volgende:
[..]
Ik weet niet zeker of dit een bewijs is, of juist iets wat uit de stelling die ik moet bewijzen volgt.
En ik weet niet zeker in hoevere ik modulo mag/kan rekenen en hoe dit samenhangt met wat ik nu ben het behandelen, dus ik zal er nog eens naar kijken.
Bedankt in ieder geval.
De getallen a en b hebben dezelfde rest na deling door 9 d.e.s.d.a. a = b (mod 9). Dus wat je kan doen is laten zien dat a gelijk is aan de som van ci modulo 9 en dan ben je klaar.
Het idee is als volgt. Stel je hebt een getal a (echt een willekeurige a, niet per se diegene waarvan we iets willen bewijzen). Noem de som van de cijfers in a voor het gemak C. Als je nu a+9 bekijkt, dan is de som van de cijfers in a+9 gelijk aan C of gelijk aan C+9 (zie vorige post). Als je modulo 9 rekent, is de som van de cijfers in a+9 gelijk aan C. Met inductie geldt dus voor iedere natuurlijk getal N dat a + 9n = Cn (mod 9) ofwel a = Cn (mod 9), waarbij Cn staat voor de som van de getallen in a + 9n.
Als je nu in plaats van a de rest r neemt, dan kan je het bewijzen.
[ Bericht 4% gewijzigd door thenxero op 05-11-2011 20:17:48 ]


Ik probeer de term modulo even te vermijden:quote:Op zaterdag 5 november 2011 20:12 schreef thenxero het volgende:
[..]
Het bewijst nog niks; het was een hint, daar vroeg je immers om. Ik zal het iets verder uitleggen.
De getallen a en b hebben dezelfde rest na deling door 9 d.e.s.d.a. a = b (mod 9). Dus wat je kan doen is laten zien dat a gelijk is aan de som van ci modulo 9 en dan ben je klaar.
Het idee is als volgt. Stel je hebt een getal a (echt een willekeurige a, niet per se diegene waarvan we iets willen bewijzen). Noem de som van de cijfers in a voor het gemak C. Als je nu a+9 bekijkt, dan is de som van de cijfers in a+9 gelijk aan C of gelijk aan C+9 (zie vorige post). Als je modulo 9 rekent, is de som van de cijfers in a+9 gelijk aan C. Met inductie geldt dus voor iedere natuurlijk getal N dat a + 9n = Cn (mod 9) ofwel a = Cn (mod 9), waarbij Cn staat voor de som van de getallen in a + 9n.
Als je nu in plaats van a de rest r neemt, dan kan je het bewijzen.
Gegeven a natuurlijk getal, met C als som van de cijfers in a.
a is deelbaar met rest door 9,dwz voor een x en een r (beide natuurljke getallen): a=x9+r
Dan heeft a+9n, voor elke n natuurlijk getal, dezelfde r, want:
a+9n=(x+n)9+r
Hetzelfde voor C, stel C heeft rest r met deling door 9:
C=9x+r
dan..(hetzelfde bewijs)
Dus rest van C is gelijk aan de rest van 'C+9n' voor elke n natuurlijk getal.
Maar hoe verbind ik ze nu (met inductie)?
[ Bericht 0% gewijzigd door Siddartha op 06-11-2011 13:27:40 ]


Als je rest niet nul is dan zeg je toch niet a is deelbaar door 9?
Hoe dan ook... De rest r is altijd in {0,...,9}. Informeel kan je daar dus 9 bij optellen totdat je bij a komt (zeg dat je n keer 9 moet optellen). Je kan ook alle cijfers van r nemen en daar steeds negen bij optellen en dat n keer doen. Dan zijn die twee getallen hetzelfde modulo 9. Volgens mij heb je daar geen inductie voor nodig. Het kan wel natuurlijk. Probeer het maar zelf af te maken zoals je zelf wil.
[ Bericht 6% gewijzigd door thenxero op 06-11-2011 12:37:16 ]
Hoe dan ook... De rest r is altijd in {0,...,9}. Informeel kan je daar dus 9 bij optellen totdat je bij a komt (zeg dat je n keer 9 moet optellen). Je kan ook alle cijfers van r nemen en daar steeds negen bij optellen en dat n keer doen. Dan zijn die twee getallen hetzelfde modulo 9. Volgens mij heb je daar geen inductie voor nodig. Het kan wel natuurlijk. Probeer het maar zelf af te maken zoals je zelf wil.
[ Bericht 6% gewijzigd door thenxero op 06-11-2011 12:37:16 ]


Als Psi(x,t=0) = B sin (2*pi*x/2a) cos (7*pi*x/2a)
Hoe kom ik dan naar Psi(x,t=0) = B / 2 * [sin (4*pi*x/a) - sin (3*pi*x/a)] ????
Hoe kom ik dan naar Psi(x,t=0) = B / 2 * [sin (4*pi*x/a) - sin (3*pi*x/a)] ????
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


ln ( p * 110 + (1-p) * 92.5) / 100 = 0.05
kan iemand mij laten zien hoe ik p oplos? In redelijk detail aub
kan iemand mij laten zien hoe ik p oplos? In redelijk detail aub
"Vanity, definitely my favorite sin. . . ."


Links en rechts met 100 vermenigvuldigen:
![ln[110p+92,5(1-p)] = 5](https://forum.fok.nl/lib/mimetex.cgi?%20ln%5B110p%2B92%2C5%281-p%29%5D%20%3D%205%20)
Dan e-macht nemen aan beide kanten:
![[110p+92,5(1-p)] = e^5](https://forum.fok.nl/lib/mimetex.cgi?%20%5B110p%2B92%2C5%281-p%29%5D%20%3D%20e%5E5%20)
Dan haakjes uitwerken:
![[110p+92,5 - 92,5p] = e^5](https://forum.fok.nl/lib/mimetex.cgi?%20%5B110p%2B92%2C5%20-%2092%2C5p%5D%20%3D%20e%5E5%20)
Dus
![[17,5p+92,5] = e^5](https://forum.fok.nl/lib/mimetex.cgi?%20%5B17%2C5p%2B92%2C5%5D%20%3D%20e%5E5%20)
Oftewel
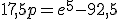
Dus
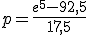
Reken maar ff na op rekenfouten, goeie oefening
Dan e-macht nemen aan beide kanten:
Dan haakjes uitwerken:
Dus
Oftewel
Dus
Reken maar ff na op rekenfouten, goeie oefening
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Er gelden rekenregels: sin(a±b) = sin(a)cos(b) ± cos(a)sin(b). Tel dit voor + en - in ± bij elkaar op, dan staat er bijna al wat je hebben moet.quote:Op dinsdag 8 november 2011 13:25 schreef maniack28 het volgende:
Als Psi(x,t=0) = B sin (2*pi*x/2a) cos (7*pi*x/2a)
Hoe kom ik dan naar Psi(x,t=0) = B / 2 * [sin (4*pi*x/a) - sin (3*pi*x/a)] ????


Maarrr, hoe krijg ik e5 uit mijn calculator?quote:Op dinsdag 8 november 2011 15:46 schreef Haushofer het volgende:
Dus
Reken maar ff na op rekenfouten, goeie oefening
Als dat 148 nog wat wordt, dan kom ik niet uit op de verwachte
ln{[px110 + (1-p)x92.50]/100} = 5%. -> p = 0.7215 (and: [1-p] = 0.2785)
"Vanity, definitely my favorite sin. . . ."

