SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Ik weet niet zeker of dit een bewijs is, of juist iets wat uit de stelling die ik moet bewijzen volgt.quote:Op zaterdag 5 november 2011 13:01 schreef thenxero het volgende:
Laten we even modulo 9 gaan denken.
0 = 9
1 = 10
2 = 11
3 = 12
4 = 13
etc
Merk op dat de som van de cijfers links steeds hetzelfde is als de som van de cijfers rechts, behalve bij 0=9.
Dus als het getal bijvoorbeeld eindigt op 23, dan kan je er rustig 9 vanafhalen en dan krijg je 14. Nog steeds geldt dan 2+3 = 1+4 dus cn+...+c0 blijft hetzelfde.
En ik weet niet zeker in hoevere ik modulo mag/kan rekenen en hoe dit samenhangt met wat ik nu ben het behandelen, dus ik zal er nog eens naar kijken.
Bedankt in ieder geval.
Het bewijst nog niks; het was een hint, daar vroeg je immers om. Ik zal het iets verder uitleggen.quote:
[..]
Ik weet niet zeker of dit een bewijs is, of juist iets wat uit de stelling die ik moet bewijzen volgt.
En ik weet niet zeker in hoevere ik modulo mag/kan rekenen en hoe dit samenhangt met wat ik nu ben het behandelen, dus ik zal er nog eens naar kijken.
Bedankt in ieder geval.
De getallen a en b hebben dezelfde rest na deling door 9 d.e.s.d.a. a = b (mod 9). Dus wat je kan doen is laten zien dat a gelijk is aan de som van ci modulo 9 en dan ben je klaar.
Het idee is als volgt. Stel je hebt een getal a (echt een willekeurige a, niet per se diegene waarvan we iets willen bewijzen). Noem de som van de cijfers in a voor het gemak C. Als je nu a+9 bekijkt, dan is de som van de cijfers in a+9 gelijk aan C of gelijk aan C+9 (zie vorige post). Als je modulo 9 rekent, is de som van de cijfers in a+9 gelijk aan C. Met inductie geldt dus voor iedere natuurlijk getal N dat a + 9n = Cn (mod 9) ofwel a = Cn (mod 9), waarbij Cn staat voor de som van de getallen in a + 9n.
Als je nu in plaats van a de rest r neemt, dan kan je het bewijzen.
[ Bericht 4% gewijzigd door thenxero op 05-11-2011 20:17:48 ]
Ik probeer de term modulo even te vermijden:quote:
[..]
Het bewijst nog niks; het was een hint, daar vroeg je immers om. Ik zal het iets verder uitleggen.
De getallen a en b hebben dezelfde rest na deling door 9 d.e.s.d.a. a = b (mod 9). Dus wat je kan doen is laten zien dat a gelijk is aan de som van ci modulo 9 en dan ben je klaar.
Het idee is als volgt. Stel je hebt een getal a (echt een willekeurige a, niet per se diegene waarvan we iets willen bewijzen). Noem de som van de cijfers in a voor het gemak C. Als je nu a+9 bekijkt, dan is de som van de cijfers in a+9 gelijk aan C of gelijk aan C+9 (zie vorige post). Als je modulo 9 rekent, is de som van de cijfers in a+9 gelijk aan C. Met inductie geldt dus voor iedere natuurlijk getal N dat a + 9n = Cn (mod 9) ofwel a = Cn (mod 9), waarbij Cn staat voor de som van de getallen in a + 9n.
Als je nu in plaats van a de rest r neemt, dan kan je het bewijzen.
Gegeven a natuurlijk getal, met C als som van de cijfers in a.
a is deelbaar met rest door 9,dwz voor een x en een r (beide natuurljke getallen): a=x9+r
Dan heeft a+9n, voor elke n natuurlijk getal, dezelfde r, want:
a+9n=(x+n)9+r
Hetzelfde voor C, stel C heeft rest r met deling door 9:
C=9x+r
dan..(hetzelfde bewijs)
Dus rest van C is gelijk aan de rest van 'C+9n' voor elke n natuurlijk getal.
Maar hoe verbind ik ze nu (met inductie)?
[ Bericht 0% gewijzigd door Siddartha op 06-11-2011 13:27:40 ]
Als je rest niet nul is dan zeg je toch niet a is deelbaar door 9?
Hoe dan ook... De rest r is altijd in {0,...,9}. Informeel kan je daar dus 9 bij optellen totdat je bij a komt (zeg dat je n keer 9 moet optellen). Je kan ook alle cijfers van r nemen en daar steeds negen bij optellen en dat n keer doen. Dan zijn die twee getallen hetzelfde modulo 9. Volgens mij heb je daar geen inductie voor nodig. Het kan wel natuurlijk. Probeer het maar zelf af te maken zoals je zelf wil.
[ Bericht 6% gewijzigd door thenxero op 06-11-2011 12:37:16 ]
Hoe dan ook... De rest r is altijd in {0,...,9}. Informeel kan je daar dus 9 bij optellen totdat je bij a komt (zeg dat je n keer 9 moet optellen). Je kan ook alle cijfers van r nemen en daar steeds negen bij optellen en dat n keer doen. Dan zijn die twee getallen hetzelfde modulo 9. Volgens mij heb je daar geen inductie voor nodig. Het kan wel natuurlijk. Probeer het maar zelf af te maken zoals je zelf wil.
[ Bericht 6% gewijzigd door thenxero op 06-11-2011 12:37:16 ]
Als Psi(x,t=0) = B sin (2*pi*x/2a) cos (7*pi*x/2a)
Hoe kom ik dan naar Psi(x,t=0) = B / 2 * [sin (4*pi*x/a) - sin (3*pi*x/a)] ????
Hoe kom ik dan naar Psi(x,t=0) = B / 2 * [sin (4*pi*x/a) - sin (3*pi*x/a)] ????
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.
ln ( p * 110 + (1-p) * 92.5) / 100 = 0.05
kan iemand mij laten zien hoe ik p oplos? In redelijk detail aub
kan iemand mij laten zien hoe ik p oplos? In redelijk detail aub
"Vanity, definitely my favorite sin. . . ."
Links en rechts met 100 vermenigvuldigen:
![ln[110p+92,5(1-p)] = 5](https://forum.fok.nl/lib/mimetex.cgi?%20ln%5B110p%2B92%2C5%281-p%29%5D%20%3D%205%20)
Dan e-macht nemen aan beide kanten:
![[110p+92,5(1-p)] = e^5](https://forum.fok.nl/lib/mimetex.cgi?%20%5B110p%2B92%2C5%281-p%29%5D%20%3D%20e%5E5%20)
Dan haakjes uitwerken:
![[110p+92,5 - 92,5p] = e^5](https://forum.fok.nl/lib/mimetex.cgi?%20%5B110p%2B92%2C5%20-%2092%2C5p%5D%20%3D%20e%5E5%20)
Dus
![[17,5p+92,5] = e^5](https://forum.fok.nl/lib/mimetex.cgi?%20%5B17%2C5p%2B92%2C5%5D%20%3D%20e%5E5%20)
Oftewel
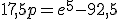
Dus
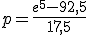
Reken maar ff na op rekenfouten, goeie oefening
Dan e-macht nemen aan beide kanten:
Dan haakjes uitwerken:
Dus
Oftewel
Dus
Reken maar ff na op rekenfouten, goeie oefening
-
Er gelden rekenregels: sin(a±b) = sin(a)cos(b) ± cos(a)sin(b). Tel dit voor + en - in ± bij elkaar op, dan staat er bijna al wat je hebben moet.quote:
Als Psi(x,t=0) = B sin (2*pi*x/2a) cos (7*pi*x/2a)
Hoe kom ik dan naar Psi(x,t=0) = B / 2 * [sin (4*pi*x/a) - sin (3*pi*x/a)] ????
Maarrr, hoe krijg ik e5 uit mijn calculator?quote:
Dus
Reken maar ff na op rekenfouten, goeie oefening
Als dat 148 nog wat wordt, dan kom ik niet uit op de verwachte
ln{[px110 + (1-p)x92.50]/100} = 5%. -> p = 0.7215 (and: [1-p] = 0.2785)
"Vanity, definitely my favorite sin. . . ."
Bij jou staat 100 nu opeens binnenin de ln. De afleiding wordt dan anders. Kijk maar eens of je eruit komt, nu je een voorbeeld hebt gezien.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
oepsie 
haakje vergeten. maar het voorbeeld verheldert veel inderdaad.
Baie dankie Haus.
haakje vergeten. maar het voorbeeld verheldert veel inderdaad.Baie dankie Haus.
"Vanity, definitely my favorite sin. . . ."
In dat geval moet je gebruiken datquote:
oepsie
Baie dankie Haus.
-
ln{[px110 + (1-p)x92.50]/100} = 5%. -> p = 0.7215 (and: [1-p] = 0.2785)
Kom er toch grotendeels niet uit
Help aub
Kom er toch grotendeels niet uit
Help aub
"Vanity, definitely my favorite sin. . . ."
Komop, gewoon de elementaire regels voor het werken met logaritmen en exponenten toepassen. En gebruik niet de letter x om vermenigvuldiging aan te geven. Wel het Andreaskruis (×) of de asterisk (*) of - bij voorkeur - de bullet operator (∙).quote:
ln{[px110 + (1-p)x92.50]/100} = 5%. -> p = 0.7215 (and: [1-p] = 0.2785)
Kom er toch grotendeels niet uit
Help aub
dat weet ik, maar zo gekopieerd, eerder had ik em wel met * maar toen vergat ik eem haakje.
Elementaire wiskunde heb ik nooit echt gehad En wat ik heb gehad is zeer roestig...
edit; Maar je moet niets ej.
Elementaire wiskunde heb ik nooit echt gehad
En wat ik heb gehad is zeer roestig...edit; Maar je moet niets ej.
"Vanity, definitely my favorite sin. . . ."
We beginnen dus met:quote:
ln{[px110 + (1-p)x92.50]/100} = 5%. -> p = 0.7215 (and: [1-p] = 0.2785)
Kom er toch grotendeels niet uit
Help aub
We nemen nu aan beide kanten de e-macht:
Dan werken we de haakjes weg:
Uitwerken levert:
Dan kunnen we p eenvoudig oplossen:
The biggest argument against democracy is a five minute discussion with the average voter.
ah, bij mijn eigen werkte ik de / 100 verkeerd weg. Vraag niet hoe
Bedankt
Bedankt
"Vanity, definitely my favorite sin. . . ."
Hoi, ik heb morgen een wiskundetoets en ik heb een eenvoudige vraag. Bij deze ongelijkheid:
16 - 1,5x < 12
-1,5x < -4
x > 2,67
Volgens mijn antwoordenboek. Mijn probleem is dat > soms naar < veranderd en andersom. Soms ook weer niet. Waar ligt dat aan? Dit staat nergens in mijn boek uitgelegd. Ik heb het geweten maar ben het nu kwijt.
16 - 1,5x < 12
-1,5x < -4
x > 2,67
Volgens mijn antwoordenboek. Mijn probleem is dat > soms naar < veranderd en andersom. Soms ook weer niet. Waar ligt dat aan? Dit staat nergens in mijn boek uitgelegd. Ik heb het geweten maar ben het nu kwijt.
Unbowed, Unbent, Unbroken.
Of je vermenigvuldigt/deelt door een negatief getal. Je kunt je antwoord makkelijk controleren: vul x=0 in.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Wacht, ik weet het weer denk ik
-1,5x < -4
Als het links een grotere waarde heeft dan rechts, is er in deze formule een < teken
x > 2,67
Hier is er links een kleinere waarde dan rechts dus moet het teken worden omgeswitchet.
-1,5x < -4
Als het links een grotere waarde heeft dan rechts, is er in deze formule een < teken
x > 2,67
Hier is er links een kleinere waarde dan rechts dus moet het teken worden omgeswitchet.
Unbowed, Unbent, Unbroken.
Wat dan? Ik begrijp niet wat je net zei. Waarom zou ik een 0 invullen?quote:
Op
Unbowed, Unbent, Unbroken.
Ziet iemand hoe ik de volgende matrix in row echelon form krijg? Ik krijg rij 1 en rij 2 niet tegelijk goed.
(2 + i, 1, 1 + i)
(2, 1 -3i, 3 -5i)
Ik kom zelf niet verder dan:
(1, 3, 2i + 6)
(0, 5 + 3i, 9i +9)
[ Bericht 20% gewijzigd door Anoonumos op 08-11-2011 22:27:11 ]
(2 + i, 1, 1 + i)
(2, 1 -3i, 3 -5i)
Ik kom zelf niet verder dan:
(1, 3, 2i + 6)
(0, 5 + 3i, 9i +9)
[ Bericht 20% gewijzigd door Anoonumos op 08-11-2011 22:27:11 ]
Leuke smiley naast je antwoordquote:
Als je nou aan beide kanten +4 en + 1,5x doet wat krijg je dan?quote:
[..]
Wat dan? Ik begrijp niet wat je net zei. Waarom zou ik een 0 invullen?
En je ze dan weer wilt omdraaien? (dus eerst van x<0 naar 0>x )?
Beneath the gold, bitter steel
Wat je hier zegt kan ik niet volgen, en in ieder geval is wat je zegt zo verwarrend dat je onherroepelijk fouten zult gaan maken. Onthoud nu maar dat het ongelijkheidsteken omklapt als je beide leden van je ongelijkheid met een negatief getal vermenigvuldigt.quote:
Wacht, ik weet het weer denk ik
-1,5x < -4
Als het links een grotere waarde heeft dan rechts, is er in deze formule een < teken
x > 2,67
Hier is er links een kleinere waarde dan rechts dus moet het teken worden omgeswitchet.
Oké, duidelijk, bedankt. Ik vind wiskunde geen moeilijk vak, maar als je vier jaar geen wiskunde hebt gehad en dan weer instapt staat niet alles kant en klaar weer voor je uitgelegd.quote:
[..]
Wat je hier zegt kan ik niet volgen, en in ieder geval is wat je zegt zo verwarrend dat je onherroepelijk fouten zult gaan maken. Onthoud nu maar dat het ongelijkheidsteken omklapt als je beide leden van je ongelijkheid met een negatief getal vermenigvuldigt.
Unbowed, Unbent, Unbroken.
Zij f' continue, laat zien d.m.v. L'Hospital dat
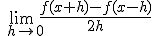=f'(x)
Na de eerste stap staat in een uitwerking d/dx (f(x+h)-f(x-h)) = f ' (x+h)+f ' (x-h). Alleen het lijkt me sterk dat dit klopt?
Na de eerste stap staat in een uitwerking d/dx (f(x+h)-f(x-h)) = f ' (x+h)+f ' (x-h). Alleen het lijkt me sterk dat dit klopt?
De clou is dat je hier een limiet bepaalt voor h naar 0. Dus h is je variabele, niet x.quote:
Zij f' continue, laat zien d.m.v. L'Hospital dat
Na de eerste stap staat in een uitwerking d/dx (f(x+h)-f(x-h)) = f ' (x+h)+f ' (x-h). Alleen het lijkt me sterk dat dit klopt?
Dus d/dh(f(x+h)-f(x-h)) en d/dh (-h) = -1, ofwel d/dh -f(x-h) = f'(x-h)? Thanks!quote:
[..]
De clou is dat je hier een limiet bepaalt voor h naar 0. Dus h is je variabele, niet x.
Edit: yep kom nu ook uit op f'(x)
Ja, dat is het. Je quotiënt is onbepaald voor h = 0, omdat teller en noemer dan beide 0 zijn, dus om de regel van L'Hôpital toe te passen differentieer je teller en noemer naar h.quote:
[..]
Dus d/dh(f(x+h)-f(x-h)) en d/dh (-h) = -1, ofwel d/dh -f(x-h) = f'(x+h)? Thanks!
Ik mag geen modulo gebruiken (dus ook niet de eigenschappen daarvan).quote:
Bedenk eerst:voor elk natuurlijk getal k.
en dan:
=
=
Maar ik kwam daarmee wel op het volgende:
Ik twijfel nog op de manier waarop ik de inductie toepas, maar ik denk wel dat dit de juiste manier is:
Als eerste geld:
Voor elke k kleiner gelijk dan n geld (k en n natuurlijke getallen):
[cn,...,ck] = 10[cn,...,ck+1] + ck
=9[cn,...,ck+1] + [cn,...,ck+1] + ck
Bekijken we dit met deling door negen naar de rest, dan blijft over:
[cn,...,ck+1] + ck
Dit principe kunnen we dus herhaald toepassen op elk natuurlijk getal a van de vorm [cn,...,c0] (met deling door 9):
[cn,...,c1]+c0
geeft
[cn,...,c2] +c1 +c0
Etc, totdat de gehele som er staat en dan ben ik klaar.
Aha met inductie kan het natuurlijk ookquote:
[..]
Ik mag geen modulo gebruiken (dus ook niet de eigenschappen daarvan).
Maar ik kwam daarmee wel op het volgende:
Ik twijfel nog op de manier waarop ik de inductie toepas, maar ik denk wel dat dit de juiste manier is:
Als eerste geld:
Voor elke k kleiner gelijk dan n geld (k en n natuurlijke getallen):
[cn,...,ck] = 10[cn,...,ck+1] + ck
=9[cn,...,ck+1] + [cn,...,ck+1] + ck
Bekijken we dit met deling door negen naar de rest, dan blijft over:
[cn,...,ck+1] + ck
Dit principe kunnen we dus herhaald toepassen op elk natuurlijk getal a van de vorm [cn,...,c0] (met deling door 9):
[cn,...,c1]+c0
geeft
[cn,...,c2] +c1 +c0
Etc, totdat de gehele som er staat en dan ben ik klaar.
eerst laten zien dat het voor het kleinste geval klopt. Dit is vrij triviaal, want [c0] is precies hetzelfde als c0.
Volgende stap. Veronderstel dat jouw bewering geldt voor een zekere n.
dus [cn,...,c0] = cn10n+cn-110n-1+...+c0100= 9k+r
en cn+cn-1+...+c0=9m+r.
Dan
[cn+1,...,c0] = cn+110n+1+cn10n+...+c0100= (*)9k+r + cn+110n+1
en
cn+1+cn+...+c0=(*)9m+r+cn+1 (1)
(*) volgt, omdat je de veronderstelt dat de stelling waar is voor n, het principe van inductie.
Dan doe ik feitelijk dezelfde stap als jij doet (en die eigenlijk ook bij modulo rekenen wordt gebruikt)
9k+r + cn+110n+1 = 9k+r + cn+110n(9+1)
= 9k+r + cn+1(10n9+10n)
= 9k+r + cn+1(10n*9+10n-1*9+10n-2)
.
.
.
= 9k+r + cn+1(10n*9+10n-1*9+...+101*9+100)
= 9k+r + 9*cn+1(10n+10n-1+...+101)+cn+1100 (2)
(1) en (2) hebben dezelfde rest, dus blijkbaar als het waar is voor een bepaalde waarde voor n, betekent dat dat het ook waar is voor n+1.
En klaar is je inductie. Technisch gezien hetzelfde als modulair rekenen, maar dan met behulp van eenvoudige rekenregels..
Ik twijfelde over het gebruik van normale inductie, zoals jij hier gebruikt, omdat ik die factor 10n+1 niet weg wist te werken. Bedankt!quote:
[..]
Aha met inductie kan het natuurlijk ook
eerst laten zien dat het voor het kleinste geval klopt. Dit is vrij triviaal, want [c0] is precies hetzelfde als c0.
Volgende stap. Veronderstel dat jouw bewering geldt voor een zekere n.
dus [cn,...,c0] = cn10n+cn-110n-1+...+c0100= 9k+r
en cn+cn-1+...+c0=9m+r.
Dan
[cn+1,...,c0] = cn+110n+1+cn10n+...+c0100= (*)9k+r + cn+110n+1
en
cn+1+cn+...+c0=(*)9m+r+cn+1 (1)
(*) volgt, omdat je de veronderstelt dat de stelling waar is voor n, het principe van inductie.
Dan doe ik feitelijk dezelfde stap als jij doet (en die eigenlijk ook bij modulo rekenen wordt gebruikt)
9k+r + cn+110n+1 = 9k+r + cn+110n(9+1)
= 9k+r + cn+1(10n9+10n)
= 9k+r + cn+1(10n*9+10n-1*9+10n-2)
.
.
.
= 9k+r + cn+1(10n*9+10n-1*9+...+101*9+100)
= 9k+r + 9*cn+1(10n+10n-1+...+101)+cn+1100 (2)
(1) en (2) hebben dezelfde rest, dus blijkbaar als het waar is voor een bepaalde waarde voor n, betekent dat dat het ook waar is voor n+1.
En klaar is je inductie. Technisch gezien hetzelfde als modulair rekenen, maar dan met behulp van eenvoudige rekenregels..
Maar je kan inductie toch ook gebruiken als je een grootste en kleinste element in een verzameling hebt? Zoals ik op het laatste doe, omdat ik aangetoond heb dat voor elke k kleiner gelijk dan n dat 'principe' geld. Al weet ik niet goed hoe ik dat wat formeler op moet schrijven.
Je pakt de limiet voor h naar 0 van f ' (x+h), dus f' moet continu zijn in x anders krijg je niet f'(x).quote:
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
als f' bestaat, hoeft f' niet continu te zijn (f is wel continu)quote:
Alleen het feit dat de afgeleide bestaat, zegt toch al dat f differentieerbaar is?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ja. Maar om te bewijzen wat Physics moest bewijzen heb je L'Hôpital niet nodig en dus ook niet dat f' continu is, want het gevraagde volgt ook direct uit de definitie van de afgeleide (maar inderdaad, de opdracht was om wél de regel van L'Hôpital te gebruiken).quote:
Vreemd is dat... maar Google kon inderdaad een tegenvoorbeeld geven.
