SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
waarom?quote:Op dinsdag 18 oktober 2011 21:15 schreef Hesitater het volgende:
- De halfwaardetijd is 5750 jaar, is het juist als ik dan dit zeg: N(5750) = 53660/2?
1,20547/10^4.quote:
Dan kom ik hierop: ln(0,5)=-k*5750 (is dit juist?)
Dan krijg ik als totale output: 1,20547
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Nou ik dacht dat als 5750 de halfwaardetijd is en je als beginwaarde 53660 hebt, het dan gehalveerd is...
Algemene oplossing voor N uitgedrukt in t en k: N(t) = 53660*e-k*t(deze formule is juist)quote:
Dan kom ik hierop: ln(0,5)=-k*5750 (is dit juist?)
Dan krijg ik als totale output: 1,20547
En de volgende vraag luidt: De halfwaardetijd van C14 is 5750 jaar. Bereken hieruit de waarde van k in 5 decimalen.
k =
- De halfwaardetijd is 5750 jaar, is het juist als ik dan dit zeg: N(5750) = 53660/2?
- Dan weet je dus de N en de t=5750
- Dan: 26830 = 53660*e-k*5750
Mijn vraag blijft staan, wat is de betekenis van N(t), en wat is k volgens jou voor getal, wat drukt dat uit?
Beneath the gold, bitter steel
De N(t) is hoeveel atomen we over hebben na een bepaalde tijd (t).
k ? Weet ik niet..
Oh het is de vervalsnelheid!
Dussss k*halfwaardetijd=ln(2) toch?
[ Bericht 32% gewijzigd door Hesitater op 18-10-2011 21:44:31 ]
k ? Weet ik niet..
Oh het is de vervalsnelheid!
Dussss k*halfwaardetijd=ln(2) toch?
[ Bericht 32% gewijzigd door Hesitater op 18-10-2011 21:44:31 ]
Je kunt gebruik maken van:quote:
Bewijs de volgende ongelijkheid:voor alle x>0
Ik weet dat ik de middelwaarde stelling moet gebruiken, maar ik kan geen ln 0 nemen. Hoe vermijd ik dit?
ln x = ∫1x dt/t
Aangezien 1/t monotoon dalend is voor t > 0 heb je dan:
(x-1)/x ≤ ln x ≤ x-1
De gelijkheid geldt alleen voor x = 1.
Bij een onderzoek naar de relatie tussen automerken en rijgedrag is de snelheid gemeten van een aantal auto’s op een weg waar 80 km/h mag worden gereden. Er zijn voor elk automerk 22 waarnemingen gedaan, samengevat levert dat:
Automerk n snelheid gemiddeld st.deviatie minimum maximum
Opel 22 76,29 4,611 70 87
Audi 22 83,42 5,492 62 103
Toyota 22 87,25 3,879 79 94
Peugeot 22 79,84 5,012 62 90
Totaal 88 81,70 6,239 62 103
a. Maak de bijbehorende variantie-analyse (ANOVA-)tabel (vermeld uw eindantwoord in het voorgestructureerde kader; gebruik het eerste kader voor uw berekeningen). Alle antwoorden tot op 2 decimalen.
Summed Square of Groups.
(4,611)-(6,239) ^ 2 = 2.65
(5,492)-(6,239) ^ 2 = 0.56
(3.879)-(6,239) ^ 2 = 5.70
(5,012)-(6,239) ^ 2 = 1.51
2.65+0.56+5.70+1.51 = 10.42
SSG=10.42
Summed Square of total
N = 88
Xbar = 81.7
Standaarddeviatie = 6.239
Squared standaarddeviatie = 38.93
N x Squared standaarddeviatie =3425.41
SST=3425.41
SSE=SST
Verder K = 4 en dan kan je alles zo invullen in een ANOVA tabel. Maar mijn vraag is nu eigenlijk of mijn SST en SSG goed berekend zijn...
Automerk n snelheid gemiddeld st.deviatie minimum maximum
Opel 22 76,29 4,611 70 87
Audi 22 83,42 5,492 62 103
Toyota 22 87,25 3,879 79 94
Peugeot 22 79,84 5,012 62 90
Totaal 88 81,70 6,239 62 103
a. Maak de bijbehorende variantie-analyse (ANOVA-)tabel (vermeld uw eindantwoord in het voorgestructureerde kader; gebruik het eerste kader voor uw berekeningen). Alle antwoorden tot op 2 decimalen.
Summed Square of Groups.
(4,611)-(6,239) ^ 2 = 2.65
(5,492)-(6,239) ^ 2 = 0.56
(3.879)-(6,239) ^ 2 = 5.70
(5,012)-(6,239) ^ 2 = 1.51
2.65+0.56+5.70+1.51 = 10.42
SSG=10.42
Summed Square of total
N = 88
Xbar = 81.7
Standaarddeviatie = 6.239
Squared standaarddeviatie = 38.93
N x Squared standaarddeviatie =3425.41
SST=3425.41
SSE=SST
Verder K = 4 en dan kan je alles zo invullen in een ANOVA tabel. Maar mijn vraag is nu eigenlijk of mijn SST en SSG goed berekend zijn...
f(x) = ln(x+1) - x + x²/2 + x³/6
Prove that: f ' (x) = x²-x³
..............................2x + 1
Ik kom er maar niet uit, zonet een uur naar lopen staren terwijl ik normaliter nooit moeite heb met afgeleiden.
x²/2 en x³/6 leidt je volgens mij zo af: 1/2 * 2x = x en 1/6 * 3x² = 0,5x² (of x²/2)
ln(x+1) = 1/x+1
en -x = -1
En vanaf daar geraak ik maar niet verder ..
btw vraag 2: Df (-1,+infinity) .. » Vind extreme waarden .. antw.boek geeft x=1 is maximum maar dat zie ik ook nog steeds niet.
Prove that: f ' (x) = x²-x³
..............................2x + 1
Ik kom er maar niet uit, zonet een uur naar lopen staren terwijl ik normaliter nooit moeite heb met afgeleiden.
x²/2 en x³/6 leidt je volgens mij zo af: 1/2 * 2x = x en 1/6 * 3x² = 0,5x² (of x²/2)
ln(x+1) = 1/x+1
en -x = -1
En vanaf daar geraak ik maar niet verder ..
btw vraag 2: Df (-1,+infinity) .. » Vind extreme waarden .. antw.boek geeft x=1 is maximum maar dat zie ik ook nog steeds niet.
Laten we bij het eerste beginnen:quote:Op woensdag 19 oktober 2011 17:51 schreef Sokz het volgende:
f(x) = ln(x+1) - x + x²/2 + x³/6
Prove that: f ' (x) = x²-x³
..............................2x + 1
Ik kom er maar niet uit, zonet een uur naar lopen staren terwijl ik normaliter nooit moeite heb met afgeleiden.
x²/2 en x³/6 leidt je volgens mij zo af: 1/2 * 2x = x en 1/6 * 3x² = 0,5x² (of x²/2)
ln(x+1) = 1/x+1
en -x = -1
En vanaf daar geraak ik maar niet verder ..
btw vraag 2: Df (-1,+infinity) .. » Vind extreme waarden .. antw.boek geeft x=1 is maximum maar dat zie ik ook nog steeds niet.
Je afgeleiden zijn goed, behalve dan dat je niet -x=-1 en ln(x+1)=1/x+1 moet schrijven, want dat ziet er een beetje vreemd uit. Let er wel op dat de afgeleide van ln(x+1) gelijk is aan 1/(x+1) en niet 1/x+1. Essentieel verschil!
Goed, laten we de dingen eens optellen:
-1+1/(x+1)+x+0.5x^2. Laten we alles gelijknamig maken:
(-(x+1) + 1 + x(x+1)+0.5x^2(x+1)) / (x+1)
=
(-x-1+1+x^2+x+0.5x^3+0.5x^2) / (x+1)
=
(1.5x^2 + 0.5x^3)/(x+1)
-> antwoord bij jouw vraag klopt niet. Kun je ook aan de noemer zien. Voor jouw afgeleide geldt dat deze niet gedefinieerd is voor x=-0.5, terwijl de functie op x=-0.5 prima differentieerbaar is.
vraag 2: Extreme waarde vind je door de afgeleide gelijk te stellen aan nul.
Succes
Zij P(A dissection B)=0.4, P(A dissection C)=0.5 en P(B dissection C)=0.6
Leidt af welke waarden P(A dissection B dissection C) kan aannemen.
Ik heb echt geen enkel idee wat ik hier moet doen en hoe.
[ Bericht 1% gewijzigd door Physics op 19-10-2011 21:04:30 ]
Leidt af welke waarden P(A dissection B dissection C) kan aannemen.
Ik heb echt geen enkel idee wat ik hier moet doen en hoe.
[ Bericht 1% gewijzigd door Physics op 19-10-2011 21:04:30 ]
P(B dissection C) wat?
Begin met een Venn-diagram.
Begin met een Venn-diagram.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik bedoel intersection idd 
Ja ik heb een venn diagram getekend etc, maar geen idee hoe ik er daadwerkelijk aan reken. Originele post aangepast, klote toetsenbord hier werkt voor geen meter.
Ja ik heb een venn diagram getekend etc, maar geen idee hoe ik er daadwerkelijk aan reken. Originele post aangepast, klote toetsenbord hier werkt voor geen meter.
A door B door C is het grootst als de cirkels zoveel mogelijk overlappen. A door B door C is het kleinst als de cirkels weinig of zelfs niet overlappen. Dus kijk in hoeverre de cirkels kunnen overlappen.
Ja stel (A intersect B) intersect (B intersect C) intersect (B intersect C) kan dit maximaal de waarde aanneme van de kleinste kans, ofwel A intersect B = 0.4. Dus dat zou dan de maximale waarde zijn, en dat hierboven is gelijk aan A intersect B intersect C.
Nu minimaal nog
Nu minimaal nog
Klopt.
edit: vraag verkeerd gelezen
Noem de kans op de doorsnede van alledrie p. Dan is p minimaal als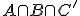
, 
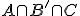en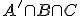 
zo groot mogelijk zijn, dus weinig overlappen in p. Dan is 
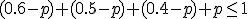, hieruit volgt dat 
.
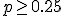[ Bericht 89% gewijzigd door twaalf op 19-10-2011 21:25:50 ]
edit: vraag verkeerd gelezen
Noem de kans op de doorsnede van alledrie p. Dan is p minimaal als
[ Bericht 89% gewijzigd door twaalf op 19-10-2011 21:25:50 ]
Dat laatste deel had ik net nodig, thanks!quote:
Klopt.
edit: vraag verkeerd gelezen
Noem de kans op de doorsnede van alledrie p. Dan is p minimaal als
Zijn er nog mensen die een poging willen wagen? Want het antwoord schijnt wel te moeten kloppen (omdat sommige klasgenoten het wél voor elkaar kregen:} )quote:
[..]
Laten we bij het eerste beginnen:
Je afgeleiden zijn goed, behalve dan dat je niet -x=-1 en ln(x+1)=1/x+1 moet schrijven, want dat ziet er een beetje vreemd uit. Let er wel op dat de afgeleide van ln(x+1) gelijk is aan 1/(x+1) en niet 1/x+1. Essentieel verschil!
Goed, laten we de dingen eens optellen:
-1+1/(x+1)+x+0.5x^2. Laten we alles gelijknamig maken:
(-(x+1) + 1 + x(x+1)+0.5x^2(x+1)) / (x+1)
=
(-x-1+1+x^2+x+0.5x^3+0.5x^2) / (x+1)
=
(1.5x^2 + 0.5x^3)/(x+1)
-> antwoord bij jouw vraag klopt niet. Kun je ook aan de noemer zien. Voor jouw afgeleide geldt dat deze niet gedefinieerd is voor x=-0.5, terwijl de functie op x=-0.5 prima differentieerbaar is.
vraag 2: Extreme waarde vind je door de afgeleide gelijk te stellen aan nul.
Succes
Ik kwam er ook niet uit nee.quote:
Het is echt niet waar; Don_Vanille geeft toch een goed argument?
Ik zal volgende week eens aan mijn leraar vragen .. antwoord houden jullie te goed!
Ik denk sowieso dat ze die x³/6 niet als 05x² schrijven maar als x²/2 (en dan gelijsktellen krijg je 2(x+1) .. maar nog 2(x+1) =/= 2x + 1quote:
wolfram geeft dit:
dit.
Lijkt er een beetje op, wss heb je haakjes niet goed.
ik zal die wolfram eens naar mijn leraar sturen via mail. Benieuwd naar zijn antwoord.
Dat zou niet uit moeten maken. Het zou ook kunnen dat je de opgave niet goed hebt overgenomen he..quote:
[..]
Ik denk sowieso dat ze die x³/6 niet als 05x² schrijven maar als x²/2 (en dan gelijsktellen krijg je 2(x+1) .. maar nog 2(x+1) =/= 2x + 1
ik zal die wolfram eens naar mijn leraar sturen via mail. Benieuwd naar zijn antwoord.
Overigens wel 'knap' dat sommige klasgenoten (onafhankelijk?) wel tot hetzelfde foute antwoord kwamen.
Dat klopt ja. Ik ben anderhalf jaar vaste klant bij het ziekenhuis geweest, dus nu begin ik weer precies waar ik gebleven was...quote:
[..]
Ik vraag me serieus af of je wel vorderingen maakt in je studie. Twee jaar geleden was je namelijk ook al bezig met dezelfde soort sommetjes over versnellingen en kromtestralen, en zo te zien ook uit precies hetzelfde boek.
Blues ain't nothing but a good man feeling bad...
Stel X is een 6 bij 2 matrix.
(6 lang, 2 breed)
Ik heb de volgende vergelijking:
B = ((X'X)^(-1)) * X'
Ik wilde de haakjes wegwerken dus: B = X^-1 * X'^-1 * X'
Maar nu neem ik de inverse van een 6 bij 2 matrix, wat niet kan.
Betekent dit dat je niet altijd eerst haakjes kan wegwerken bij matricen?
(6 lang, 2 breed)
Ik heb de volgende vergelijking:
B = ((X'X)^(-1)) * X'
Ik wilde de haakjes wegwerken dus: B = X^-1 * X'^-1 * X'
Maar nu neem ik de inverse van een 6 bij 2 matrix, wat niet kan.
Betekent dit dat je niet altijd eerst haakjes kan wegwerken bij matricen?
Precies dat. Alleen als A en B vierkant en inverteerbaar zijn, kun je bij (AB)-1 (AB is dan ook inverteerbaar, kun je aantonen; je kunt ook aannemen dat AB inverteerbaar is waaruit volgt dat A en B dat ook zijn mits A en B vierkant zijn) de haakjes wegwerken.quote:
Betekent dit dat je niet altijd eerst haakjes kan wegwerken bij matricen?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Nog een vraagje dan maar
Stel ik wil optimaliseren onder constraint en m'n lagrange functie is:
L(k,x,y) = 3xy - k*(x^2-y^2-8)
Eerste order condities
L'x = 3y - k2x = 0
L'y = 3x - k2y = 0
L'k = -(x^2-y^2-8) = 0
k = 3y/2x en k 3x/2y en dan oplossen enzovoort.
Ik vroeg aan de docent waarom je niet moet zeggen dat 2x =! 0 en 2y =! 0 is, aangezien je anders door nul deelt. De docent zei dat dat kon, maar niet hoefden aangezien x of y toch niet 0 zijn.
Waarom weet de docent dit zo snel?
Ik vraag dit omdat ik vaak vergeet om die stationaire punten waar x = 0 mee te nemen.
Zoals hier bijvoorbeeld:
(Dit is wel een iets andere som aangezien er alleen y in de 2de vergelijking is maar kan geen beter voorbeeld vinden).
L(k,x,y) = x^2 + y^2 - 2x + 1 - k*(x^2 + 4y^2 - 16)
Eerste order condities:
L'x = 2x - 2 - k*2x = 0
L'y = 2y - k*8y = 0
L'k = -(x^2 - 4y^2 - 16) = 0
Stel ik neem de 2de vergelijking 2y - k*8y = 0
Ik deed dan simpelweg k = 8y/2y = 1/4 en vergat dat y = 0 ook een oplossing is.
Stel ik wil optimaliseren onder constraint en m'n lagrange functie is:
L(k,x,y) = 3xy - k*(x^2-y^2-8)
Eerste order condities
L'x = 3y - k2x = 0
L'y = 3x - k2y = 0
L'k = -(x^2-y^2-8) = 0
k = 3y/2x en k 3x/2y en dan oplossen enzovoort.
Ik vroeg aan de docent waarom je niet moet zeggen dat 2x =! 0 en 2y =! 0 is, aangezien je anders door nul deelt. De docent zei dat dat kon, maar niet hoefden aangezien x of y toch niet 0 zijn.
Waarom weet de docent dit zo snel?
Ik vraag dit omdat ik vaak vergeet om die stationaire punten waar x = 0 mee te nemen.
Zoals hier bijvoorbeeld:
(Dit is wel een iets andere som aangezien er alleen y in de 2de vergelijking is maar kan geen beter voorbeeld vinden).
L(k,x,y) = x^2 + y^2 - 2x + 1 - k*(x^2 + 4y^2 - 16)
Eerste order condities:
L'x = 2x - 2 - k*2x = 0
L'y = 2y - k*8y = 0
L'k = -(x^2 - 4y^2 - 16) = 0
Stel ik neem de 2de vergelijking 2y - k*8y = 0
Ik deed dan simpelweg k = 8y/2y = 1/4 en vergat dat y = 0 ook een oplossing is.
Van welk optimalisatieprobleem krijg je die lagrangian? 
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
1ste f(x,y) = 3xy
onder constraint x^2 -y^2 - 8 = 0
2de
f(x,y) x^2 + y^2 -2x + 1
onder constraint x^2 + 4y^2 - 16 = 0
onder constraint x^2 -y^2 - 8 = 0
2de
f(x,y) x^2 + y^2 -2x + 1
onder constraint x^2 + 4y^2 - 16 = 0
Je vergeet de objective (min/max) nog.
Bij de 1ste zie je gelijk dat x=0 of y=0 niet optimaal is, dat is de reden dat je dat direct kunt vergeten.
Bij de 1ste zie je gelijk dat x=0 of y=0 niet optimaal is, dat is de reden dat je dat direct kunt vergeten.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Aha, dus enkel in situaties waar je het gelijk kan aflezen van f(x,y) kan je dit soort voorwaarden weglaten?quote:
[b][b]Je vergeet de objective (min/max) nog.[/b][/b]
Bij de 1ste zie je gelijk dat x=0 of y=0 niet optimaal is, dat is de reden dat je dat direct kunt vergeten.
Stel dat je het niet in één keer zag bij de 1ste situatie? Zou je dan wel eerst x = 0 en y = 0 als punt moeten nemen en dan erachter komen dat dit invullen in de derde vergelijking (L'k) er dan staat 0 = 8 en dat dit punt dus afvalt?
Je moet een punt pakken dat niet voldoet aan 2x =! 0 en 2y =! 0. Dat zijn meer punten dan het punt waarvoor geldt x=0 en y=0.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Werk het eens uit met de definitie van de voorwaardelijke kans.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Oh, je kunt niet zeggen dat het >= is, de stelling is dus niet waar.quote:
Ik wilde eigenlijk alleen maar het eindantwoord ter controle
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Er staat kleiner of gelijk.quote:
[..]
Oh, je kunt niet zeggen dat het >= is, de stelling is dus niet waar.
Geldt hetzelfdequote:
De stelling kan best juist zijn, maar het hangt af van je keuze voor A, B, C en je kansmaat.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Hallo allen, wiskundig gezien ben ik echt dyslectisch... Ik heb de volgende formule:
y = 0.8 [ y - (0.3 y + 20)] + 20 + 120 + 200 + [(208 - ( 0.2 y + 20)]
Nu staat er in het antwoordblad als volgende stap:
y = 0.8 [ y - (0.3 y + 20)] + 20 + 120 + 200 + 208 - 0.2 y - 20
Mijn vraag is, hoe kan je die haakjes zomaar weghalen? Waarom moet het niet uiteindelijk worden:
y = 0.8y - 0.24 y - 16 + 20 + 120 + 200 + 208 - 0.16 y - 16
y = 0.8 [ y - (0.3 y + 20)] + 20 + 120 + 200 + [(208 - ( 0.2 y + 20)]
Nu staat er in het antwoordblad als volgende stap:
y = 0.8 [ y - (0.3 y + 20)] + 20 + 120 + 200 + 208 - 0.2 y - 20
Mijn vraag is, hoe kan je die haakjes zomaar weghalen? Waarom moet het niet uiteindelijk worden:
y = 0.8y - 0.24 y - 16 + 20 + 120 + 200 + 208 - 0.16 y - 16
Het eerste deel van je antwoord klopt, alleen de laatste twee termen zijn fout. Je vermenigvuldigt ze met 0.8, maar je hoeft alleen [y - (0.3 y + 20)] met 0.8 te vermenigvuldigen.quote:
Hallo allen, wiskundig gezien ben ik echt dyslectisch... Ik heb de volgende formule:
y = 0.8 [ y - (0.3 y + 20)] + 20 + 120 + 200 + [(208 - ( 0.2 y + 20)]
Nu staat er in het antwoordblad als volgende stap:
y = 0.8 [ y - (0.3 y + 20)] + 20 + 120 + 200 + 208 - 0.2 y - 20
Mijn vraag is, hoe kan je die haakjes zomaar weghalen? Waarom moet het niet uiteindelijk worden:
y = 0.8y - 0.24 y - 16 + 20 + 120 + 200 + 208 - 0.16 y - 16
The biggest argument against democracy is a five minute discussion with the average voter.
Ik vind het wel apart dat je wel doorhebt dat je 20, 120, 200, 208 niet met 0.8 moet vermenigvuldigen maar dan wel die laatste term weer gaat vermenigvuldigen met 0.8.
oke, maar waarom wordt het bij die laatste term dan wel -20 en niet ook -280 ? Je haalt toch bij beide de haakjes weg?quote:
[..]
Het eerste deel van je antwoord klopt, alleen de laatste twee termen zijn fout. Je vermenigvuldigt ze met 0.8, maar je hoeft alleen [y - (0.3 y + 20)] met 0.8 te vermenigvuldigen.
hah, ja nu je het zegt. Ik heb dat soort dingen gewoon niet door. Wiskunde is echt niet mijn ding.quote:Op vrijdag 21 oktober 2011 19:32 schreef thenxero het volgende:
Ik vind het wel apart dat je wel doorhebt dat je 20, 120, 200, 208 niet met 0.8 moet vermenigvuldigen maar dan wel die laatste term weer gaat vermenigvuldigen met 0.8.
Waar haal je dan die extra - vandaan ? En je bedoelde zeker 208.quote:
[..]
oke, maar waarom wordt het bij die laatste term dan wel -20 en niet ook -280 ? Je haalt toch bij beide de haakjes weg?
[..]
hah, ja nu je het zegt. Ik heb dat soort dingen gewoon niet door. Wiskunde is echt niet mijn ding.
idd 208. Ik vat eigenlijk niet waarom je van +20 naar -20 gaat. Ik weet dat het te maken heeft met het weghalen van de haakjes, maar waarom veranderd het getal 20 dan van positief naar negatief en verandert 208 niet?quote:
[..]
Waar haal je dan die extra - vandaan ? En je bedoelde zeker 208.
Het minteken is dus van toepassing op alles binnen de ronde haakjes, niet alleen op 0.2y. Dat zorgt ervoor dat er -1*0.2y + -1*20 komt te staan als je de haakjes wegwerkt. Die +- wordt dan een -. Je krijgt ook een - als er -+ staat. Krijg je daarentegen ++ of - -, dan kun je dat vervangen door een +.quote:
[..]
idd 208. Ik vat eigenlijk niet waarom je van +20 naar -20 gaat. Ik weet dat het te maken heeft met het weghalen van de haakjes, maar waarom veranderd het getal 20 dan van positief naar negatief en verandert 208 niet?
-(a+b) = - a - b
Waarom?
-(a+b) = -1 * (a+b) = -1*a + -1*b = - a - b, waarbij we gebruik maken van de regel c(a+b) = ca + cb.
Waarom?
-(a+b) = -1 * (a+b) = -1*a + -1*b = - a - b, waarbij we gebruik maken van de regel c(a+b) = ca + cb.
. Bedankt mensen!
Luitjes,
Ik heb een klein probleempje. Ik moet de formule opstellen van dX + dY = f, waarbij d, e en f breuken zijn.
Een van de coördinaten is gegeven, (-1, 0)
Het andere punt ligt op deze lijn:
(x*, y*) moet rationaal zijn.
Als ik naar een simpele schets van mijn eenheidscirkel keek sprong x = 1/2 naar voren. Hieruit volgde dat y^2 = 3/4 dus y = 1/2√3
Tipje van de sluier graag
Ik heb een klein probleempje. Ik moet de formule opstellen van dX + dY = f, waarbij d, e en f breuken zijn.
Een van de coördinaten is gegeven, (-1, 0)
Het andere punt ligt op deze lijn:
(x*, y*) moet rationaal zijn.
Als ik naar een simpele schets van mijn eenheidscirkel keek sprong x = 1/2 naar voren. Hieruit volgde dat y^2 = 3/4 dus y = 1/2√3
Tipje van de sluier graag
Mag je in het plaatje gaan meten dan? Want dan snap ik niet echt het nut van deze opdrachtquote:
Luitjes,
Ik heb een klein probleempje. Ik moet de formule opstellen van dX + eY = f, waarbij d, e en f breuken zijn.
Een van de coördinaten is gegeven, (-1, 0)
Het andere punt ligt op deze lijn:
[ afbeelding ]
(x*, y*) moet rationaal zijn.
Als ik naar een simpele schets van mijn eenheidscirkel keek sprong x = 1/2 naar voren. Hieruit volgde dat y^2 = 3/4 dus y = 1/2√3
Tipje van de sluier graag
Beneath the gold, bitter steel
Nee. Maar het is wel duidelijk dat ik de waarden x = 1/2 en y = 1/2√ 3 diende te nemen.quote:
[..]
Mag je in het plaatje gaan meten dan? Want dan snap ik niet echt het nut van deze opdracht
Dus de bedoeling is gewoon een vergelijking voor de lijn door die 2 punten?
Beneath the gold, bitter steel
Ja, toch wel. Vraag fout gelezen vrees ik.quote:
Dus de bedoeling is gewoon een vergelijking voor de lijn door die 2 punten?
Mijn GR gaat dit probleempje eens bekijken.
Nou ten eerste is je tweede coordinaat niet helemaal correct, want je zit toch echt in de negatieve y-as...quote:
[..]
Ja, toch wel. Vraag fout gelezen vrees ik.
Mijn GR gaat dit probleempje eens bekijken.
Beneath the gold, bitter steel
Ik bedoel natuurlijk -.5sqrt(3).....quote:
[..]
Nou ten eerste is je tweede coordinaat niet helemaal correct, want je zit toch echt in de negatieve y-as...
Inderdaad. De vraagstelling van Amoeba is ook incompleet. Hij denkt kennelijk dat er maar één lijn is die aan het gestelde voldoet, maar dat is niet zo. Er liggen oneindig veel punten in ieder kwadrant op de eenheidscirkel waarvan de coördinaten rationaal zijn.quote:
[..]
y* moest toch rationaal zijn? In dat geval is y* dat zeker niet.
Ik moet een tegenvoorbeeld vinden voor
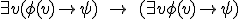
Ik moet zelf een taal L, structuur M en formules phi en psi bedenken zodat het niet klopt. Wie kan me helpen?
Ik moet zelf een taal L, structuur M en formules phi en psi bedenken zodat het niet klopt. Wie kan me helpen?
't Is een implicatie. Wanneer is deze niet waar?quote:
Ik moet een tegenvoorbeeld vinden voor
Ik moet zelf een taal L, structuur M en formules phi en psi bedenken zodat het niet klopt. Wie kan me helpen?
Als de linkerkant wel waar is en de rechterkant niet.quote:
[..]
't Is een implicatie. Wanneer is deze niet waar?
De rechterkant is ook weer een implicatie. Die moet dus niet waar zijn. Daaruit kun je wederom conclusies trekken.quote:
[..]
Als de linkerkant wel waar is en de rechterkant niet.
Ja... maar ik zoek eigenlijk een tegenvoorbeeld he.
Ik heb nu alle implicaties eruit gehaald maar ik zie niet hoe dat helpt:
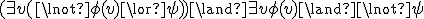
TeX kan hier blijkbaar niet alle logische symbolen weergeven.
[ Bericht 81% gewijzigd door thenxero op 24-10-2011 21:32:34 ]
Ik heb nu alle implicaties eruit gehaald maar ik zie niet hoe dat helpt:
TeX kan hier blijkbaar niet alle logische symbolen weergeven.
[ Bericht 81% gewijzigd door thenxero op 24-10-2011 21:32:34 ]
Een vraag uit een oefententamen:
Alvast dank!
Mijn antwoord:quote:Let S = [-1, 1] x [-1, 1] and C = { (x, y) | x2 + y2 <= 1 }.
Prove that |C| = |S|.
Hoe noteer ik dit eerste verhaal, over de bijectie, kort en duidelijk? Of moet ik gewoon dit verhaal uitleggen?quote:De eerste set kan je zien als alle elementen binnen of op de rand van een vierkant, de tweede set als alle elementen binnen of op de rand van een cirkel (waarschijnlijk hebben ze daarom ook C en S als letters voor de verzamelingen gekozen).
Ik zie dat er een injectieve functie bestaat van S naar C en omgekeerd. Van S naar C: Definieer r als (.5 + s1 / 2) waar s1 het eerste element uit het tupel uit S is, en a als (pi * s2 + pi) waar s2 het tweede element uit het tupel uit S is. Het bijbehorende tupel uit C is dan (r*cos(a), r*sin(a)).
De injectieve functie van C naar S is. (arctan2(c1, c2), sqrt(c12 + x22)) met c1 het eerste element uit het tupel uit C en c2 het tweede element uit het tupel uit C.
En omdat er een injectieve functie van C naar S is en andersom, geldt:
|C| <= |S|
|S| <= |C|
en volgens het theorem van Cantor-Schroeder-Bernstein ook:
|C| = |S|
Alvast dank!
Finally, someone let me out of my cage
Het punt (-1,0) van het vierkant wordt op hetzelfde punt afgebeeld als het punt (-1,1) van het vierkant.
[ Bericht 1% gewijzigd door twaalf op 25-10-2011 16:42:28 ]
[ Bericht 1% gewijzigd door twaalf op 25-10-2011 16:42:28 ]
Oh crapquote:
Het punt (-1,0) van het vierkant wordt op hetzelfde punt afgebeeld als het punt (-1,1) van het vierkant.
Finally, someone let me out of my cage
Ik snap het al, je mag stellen |C| <= |S| omdat elk tupel in C ook in S zit, en dan gebruik je (ik leg het even geometrisch uit) een geschaald vierkant (bijvoorbeeld: [-.5, 5]2) en gebruik je dat elk geordend tupel uit het geschaalde vierkant in de cirkel zit.
Maar hoe noteer je nou een concrete functie die als domein C heeft en als codomein S (of andersom, of nog meer in het algemeen een functie die twee verzameling geordende n-tupels met n > 1 op elkaar afbeeldt, om het maar even wiskundig uit te drukken).
Maar hoe noteer je nou een concrete functie die als domein C heeft en als codomein S (of andersom, of nog meer in het algemeen een functie die twee verzameling geordende n-tupels met n > 1 op elkaar afbeeldt, om het maar even wiskundig uit te drukken
).
Finally, someone let me out of my cage
Het bereik is
De functie is injectief, want...
Het bereik is
De functie is injectief, want...
Kan iemand mij het nut van het berekenen van een limit van een functie uitleggen? Je bepaalt dus de waarde die een bepaalde functie nooit zal bereiken, maar wat heb je daar aan?
Of wel, als de functie continu is in dat punt. Limieten zijn heel belangrijk, bijvoorbeeld voor de afgeleide (waarbij de functie zelf continu moet zijn).quote:Op dinsdag 25 oktober 2011 18:48 schreef Burbujas het volgende:
Kan iemand mij het nut van het berekenen van een limit van een functie uitleggen? Je bepaalt dus de waarde die een bepaalde functie nooit zal bereiken
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
klein voorbeeldje:quote:
Kan iemand mij het nut van het berekenen van een limit van een functie uitleggen? Je bepaalt dus de waarde die een bepaalde functie nooit zal bereiken, maar wat heb je daar aan?
g(x) = sin(x) is een relatief lelijke functie
f(x) = x is een relatief makkelijke functie
als je de limiet x ->0 pakt van sin(x)/x kun je laten zien dat deze limiet gelijk is aan 1. Dit betekent dus dat sin(x) zich in de buurt van x=0 gedraagt als de functie f(x) = x en je dus voor kleine waarden van x kunt zeggen: sin(x) is ongeveer gelijk aan x.
Ander voorbeeld:
Asymptoten berekenen gaat met behulp van limieten.
Ik denk dat limieten wel het belangrijkst zijn voor differentiëren, zoals glowmouse al noemde. De afgeleide van een functie is namelijk gedefinieerd als een limiet:
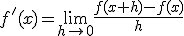
Als het goed is moet ik het doen via de epsilon-delta definitie.quote:Problem:
Let f, g: ℝ -> ℝ be continuous functions. Prove: For all α > 0 and β > 0, the function F: ℝ -> ℝ defined by F(x) = α * f(x) + β * g(x) is continuous.
Dit is wat ik tot nu toe heb:
Maar dat lijkt me dus veel te simpel. Pak ik het totaal verkeerd aan?quote:Because it is given that f(x) is continuous, it follows through the epsilon-delta definition that there exists a δ for which δ > |x-p| ≥ |f(x)-f(p)| holds. Then, it follows that δ * α > α * |x-p| ≥ α * |f(x)-f(p)|, which implies that f(x) * α is continuous if you choose α times the δ for which f(x) was continuous, as the δ for f(x) * α.
Özil | Ki SY| Son HM| Lee SW| Taeguk Warriors|
Nee, dit gaat al verkeerd. Uit de ε,δ definitie van continuïteit volgt helemaal niet wat jij hier beweert. Als je functie f: R ↦ R continu is in x = p, dan bestaat er voor elke ε > 0 een δ > 0 zodanig dat | f(x) - f(p) | < ε voor elke x zodanig dat | x - p | < δ. Maar dat impliceert niet wat jij stelt.quote:
[..]
Als het goed is moet ik het doen via de epsilon-delta definitie.
Dit is wat ik tot nu toe heb:
Because it is given that f(x) is continuous, it follows through the epsilon-delta definition that there exists a δ for which δ > |x-p| ≥ |f(x)-f(p)| holds.
[snip]
Ik zie het, jij hebt inderdaad de correcte, volledige definitie, ik maakte fouten.quote:
[..]
Nee, dit gaat al verkeerd. Uit de ε,δ definitie van continuïteit volgt helemaal niet wat jij hier beweert. Als je functie f: R ↦ R continu is in x = p, dan bestaat er voor elke ε > 0 een δ > 0 zodanig dat | f(x) - f(p) | < ε voor elke x zodanig dat | x - p | < δ. Maar dat impliceert niet wat jij stelt.
Als ik een simpele functie krijg als f(x)=sqrt(x) kan ik ook wel bewijzen of deze wel of niet continuous is in het punt P, door op zoek te gaan naar, zoals jij stelt, de δ waaruit blijkt dat |p - x| < δ impliceert dat |f(p) - f(x)| < ε waar gegeven is dat ε > 0 en δ > 0.
Ik probeer die methode nu op mijn probleem toe te passen. Mij lijkt het dan dat ik in dit geval de δ moet vinden waardoor δ > |p - x| impliceert dat ε > |f(p)*α-f(x)*α|, waar gegeven is dat ε > 0 en δ > 0.
En dan loop ik dus vast, omdat ik niet zou weten hoe ik die δ zou moeten vinden.
Ik kom niet verder dan |*f(x)-*f(p)|<|*f(p)-*f(p+δ)|
[ Bericht 1% gewijzigd door Thas op 26-10-2011 06:34:19 ]
Özil | Ki SY| Son HM| Lee SW| Taeguk Warriors|
Je moet juist niet op zoek gaan naar de delta, maar naar de epsilon. Uiteindelijk moet je de som nemen van twee functies, en daar moet iets uitkomen dat kleiner is dan epsilon. Logisch is dan om te kijken naar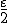 
. Als je uitgaat van een bepaalde epsilon waaraan f+g moet voldoen, dan kun je voor 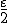een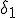 
vinden voor f en een 
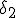vinden voor g.
Vergeef mijn domheid, maar ik volg het niet helemaal (voorkennis slechts vwo Wiskunde A ).
). quote:
[..]
Of wel, als de functie continu is in dat punt. Limieten zijn heel belangrijk, bijvoorbeeld voor de afgeleide (waarbij de functie zelf continu moet zijn).
Afgeleiden berekenen kan toch ook zonder je het limiet weet? (tenminste dat is hoe we op dit moment afgeleiden berekenen). En wat bedoel je met een functie die continu is?quote:
Ik denk dat limieten wel het belangrijkst zijn voor differentiëren, zoals glowmouse al noemde. De afgeleide van een functie is namelijk gedefinieerd als een limiet:
Dus door het limiet te bepalen kun je in sommige gevallen een ingewikkelde functie benaderen door dezelfde waarde in een simpelere functie in te vullen? Is dat het voordeel?quote:
[..]
klein voorbeeldje:
g(x) = sin(x) is een relatief lelijke functie
f(x) = x is een relatief makkelijke functie
als je de limiet x ->0 pakt van sin(x)/x kun je laten zien dat deze limiet gelijk is aan 1. Dit betekent dus dat sin(x) zich in de buurt van x=0 gedraagt als de functie f(x) = x en je dus voor kleine waarden van x kunt zeggen: sin(x) is ongeveer gelijk aan x.
Ander voorbeeld:
Asymptoten berekenen gaat met behulp van limieten.
Het gaat er niet om dat je voor een 'gegeven' ε > 0 aantoont dat er zo'n δ is, maar dat je aantoont dat er voor elke ε > 0 een δ > 0 bestaat zodanig dat | f(x) - f(p) | < ε indien | x - p | < δ. Je moet dus een existentiebewijs leveren, en dat niet voor één ε > 0 maar voor elke ε > 0. In het algemeen doe je dat door te laten zien dat je bij elke ε > 0 een δ > 0 kunt construeren die aan het gestelde voldoet.quote:
[..]
Ik zie het, jij hebt inderdaad de correcte, volledige definitie, ik maakte fouten.
Als ik een simpele functie krijg als f(x)=sqrt(x) kan ik ook wel bewijzen of deze wel of niet continu is in het punt P, door op zoek te gaan naar, zoals jij stelt, de δ waaruit blijkt dat |x - p| < δ impliceert dat |f(p) - f(x)| < ε waar gegeven is dat ε > 0 en δ > 0.
Gegeven is dat f: R ↦ R en g: R ↦ R continue functies zijn. Gevraagd wordt nu te bewijzen dat de functie F: R ↦ R gedefinieerd door F(x) = α∙f(x) + β∙g(x) met α,β > 0 eveneens continu is op R.quote:[snip]
De continuïteit van f en g op R houdt in dat f en g continu zijn in elk punt op R. We kunnen daarom volstaan met aan te tonen dat de continuïteit van f en g voor een willekeurige x = p de continuïteit van F in x = p impliceert.
De continuïteit van f in x = p impliceert per definitie dat er voor elke εf > 0 een δf > 0 bestaat zodanig dat:
(1) | f(x) - f(p) | < εf voor | x - p | < δf
En de continuïteit van g in x = p impliceert evenzo dat er voor elke εg > 0 een δg > 0 bestaat zodanig dat:
(2) | g(x) - g(p) | < εg voor | x - p | < δg
We kiezen nu een willekeurige ε > 0 en kiezen dan vervolgens:
(3) εf = ε/2α en εg = ε/2β
Aangezien ε > 0 en tevens α,β > 0 volgt uit (3) dat ook εf > 0 en εg > 0. En dus bestaan er op grond van de continuïteit van f en g in x = p een δf > 0 en een δg > 0 waarmee voldaan wordt aan (1) resp. (2). Vermenigvuldiging van de leden van de eerste ongelijkheid in (1) met α resp. vermenigvuldiging van de leden van de eerste ongelijkheid in (2) met β levert nu dat geldt:
(4) | α∙f(x) - α∙f(p) | < α∙εf = ε/2 voor | x - p | < δf
En:
(5) | β∙g(x) - β∙g(p) | < β∙εg = ε/2 voor | x - p | < δg
Zij nu δ = min(δf,δg). Dan is δ ≤ δf en tevens δ ≤ δg zodat uit (4) en (5) volgt dat ook geldt:
(6) | α∙f(x) - α∙f(p) | < ε/2 voor | x - p | < δ
En:
(7) | β∙g(x) - β∙g(p) | < ε/2 voor | x - p | < δ
Optelling van de leden van de eerste ongelijkheden in (6) en(7) levert nu dat geldt:
(8) | α∙f(x) - α∙f(p) | + | β∙g(x) - β∙g(p) | < ε voor | x - p | < δ
En op grond van de driehoeksongelijkheid geldt ook:
(9) | (α∙f(x) + β∙g(x)) - (α∙f(p) + β∙g(p)) | ≤ | α∙f(x) - α∙f(p) | + | β∙g(x) - β∙g(p) |
Uit (8) en (9) alsmede F(x) = α∙f(x) + β∙g(x) volgt aldus dat:
(10) | F(x) - F(p) | < ε voor | x - p | < δ
Aangezien ε > 0 willekeurig was gekozen hebben we nu laten zien dat er voor elke ε > 0 een δ > 0 is te vinden waarmee aan (10) wordt voldaan, en dat betekent niets anders dan dat F continu is in x = p,
QED
Kun je een opgave mbt lineair programmeren ook makkelijk zonder grafieken oplossen?
Bij onderstaand voorbeeld kom ik ook tot de volgende regels:
Doelfunctie:
Maximaliseer: C = 5a + 4b
Voorwaarden:
Xeneen: 8a + 4b ≤ 16000
Ypreen: 2a + 6b ≤ 12000
Arbeid: 5a + 6b ≤ 15000
a ≥ 0
b ≥ 0
Echter lossen ze het daarna op met door middel van grafiekjes. Kan dit dus ook zonder grafiekjes?
Opgave: http://www.wiskundebijles(...)air_programmeren.htm
Bij onderstaand voorbeeld kom ik ook tot de volgende regels:
Doelfunctie:
Maximaliseer: C = 5a + 4b
Voorwaarden:
Xeneen: 8a + 4b ≤ 16000
Ypreen: 2a + 6b ≤ 12000
Arbeid: 5a + 6b ≤ 15000
a ≥ 0
b ≥ 0
Echter lossen ze het daarna op met door middel van grafiekjes. Kan dit dus ook zonder grafiekjes?
Opgave: http://www.wiskundebijles(...)air_programmeren.htm
http://nl.wikipedia.org/wiki/Simplexmethodequote:
Kun je een opgave mbt lineair programmeren ook makkelijk zonder grafieken oplossen?
Bij onderstaand voorbeeld kom ik ook tot de volgende regels:
Doelfunctie:
Maximaliseer: C = 5a + 4b
Voorwaarden:
Xeneen: 8a + 4b ≤ 16000
Ypreen: 2a + 6b ≤ 12000
Arbeid: 5a + 6b ≤ 15000
a ≥ 0
b ≥ 0
Echter lossen ze het daarna op met door middel van grafiekjes. Kan dit dus ook zonder grafiekjes?
Opgave: http://www.wiskundebijles(...)air_programmeren.htm
edit: ik bekijk nu pas je link. Ze komen bij de a=1285.71 en b= 1428.57 door ook naar de figuur te kijken, anders weet je niet welke voorwaardevergelijkingen je moet oplossen. Hoe ze het in jouw link doen, heb je dus nog steeds de grafiekjes nodig. Het kan wel zonder, met het simplexalgoritme, maar dat is wel veel werk.
[ Bericht 12% gewijzigd door freiss op 26-10-2011 16:37:25 ]
HJ 14-punt-gift.
Lijst met rukmateriaal!
Lijst met rukmateriaal!
Maak er eens getallen van? Dus eerst de delingen doen, daarna pas de macht verheffen?
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.
187 gedeeld door 555, dat is 0,3369 dat doe je vervolgens tot de macht 0,2 (is immers hetzelfde als 1/5) en voila 0,804
aight bedankt manquote:
187 gedeeld door 555, dat is 0,3369 dat doe je vervolgens tot de macht 0,2 (is immers hetzelfde als 1/5) en voila 0,804
kan ik verder met de berekening
Zoek de handleiding van je calculator eens op ...quote:
[ link | afbeelding ]
weten jullie hoe ik op het antwoord kom? ik kom steeds op andere getallen.
thx
Bedankt voor je reactie. Helaas dus geen simpele oplossing!quote:Op woensdag 26 oktober 2011 16:28 schreef freiss het volgende:
[..]
http://nl.wikipedia.org/wiki/Simplexmethode
edit: ik bekijk nu pas je link. Ze komen bij de a=1285.71 en b= 1428.57 door ook naar de figuur te kijken, anders weet je niet welke voorwaardevergelijkingen je moet oplossen. Hoe ze het in jouw link doen, heb je dus nog steeds de grafiekjes nodig. Het kan wel zonder, met het simplexalgoritme, maar dat is wel veel werk.
