SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Het nadeel van een bewijs met inductie is dat het niet heuristisch is, dus je moet al weten wat de formule is voor e.g. de som van de kwadraten of kubieken (derde machten) van de eerste n natuurlijke getallen alvorens je een bewijs met inductie kunt geven. Een afleiding van een dergelijke formule is toch wat anders. In dit geval weet Physics al wat hij moet bewijzen, en is gebruik van inductie dus inderdaad de aangewezen weg, maar eerder vroeg Physics ook al naar een uitdrukking voor de som van de kwadraten van de eerste n natuurlijke getallen en hoe je aan die formule komt, en dan is het geven van de kant en klare formule met de opmerking dat je deze kunt bewijzen met inductie geen antwoord op de eigenlijke vraag.quote:Op zaterdag 15 oktober 2011 12:16 schreef GlowMouse het volgende:
Het mag wel (want het is makkelijk aan te tonen), maar ik vraag me af of inductie niet simpeler is.
[ Bericht 0% gewijzigd door Riparius op 15-10-2011 20:01:30 ]
Ja, en dat is inderdaad zelfs handig als je het gevraagde middels inductie wil bewijzen. Als je wil zien waarom en hoe het bewijs dan gaat moet je maar even hier kijken. Wil je daarentegen een afleiding van de somformule zonder gebruik van inductie, dan kan ik je aanraden eens naar het verschil van de vierde machten van opeenvolgende natuurlijke getallen te kijken en deze verschillen te sommeren. Je krijgt dan een zogeheten telescoopreeks waarin alle termen uitgezonderd de eerste en de laatste tegen elkaar weg vallen.quote:
Bewijs dat de som van k=1 t/m N met k^3 gelijk is aan (de som van k=1 t/m N met k)^2
Mag ik dan gebruiken dat de som van k=1 t/m N met k gelijk is aan 1/2n(n+1)?
Ik zie dat je met inductie ook de somformule nodig hebt van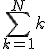 
. Met die formule is het bewijs vijf regeltjes.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik heb eerst die somformule bewezen en daarmee de oorspronkelijke vraag bewezen dmv volledige inductie.quote:
Ik zie dat je met inductie ook de somformule nodig hebt van
Ja bedankt, het is me zelf ook al gelukt!quote:
[..]
Ja, en dat is inderdaad zelfs handig als je het gevraagde middels inductie wil bewijzen. Als je wil zien waarom en hoe het bewijs dan gaat moet je maar even hier kijken. Wil je daarentegen een afleiding van de somformule zonder gebruik van inductie, dan kan ik je aanraden eens naar het verschil van de vierde machten van opeenvolgende natuurlijke getallen te kijken en deze verschillen te sommeren. Je krijgt dan een zogeheten telescoopreeks waarin alle termen uitgezonderd de eerste en de laatste tegen elkaar weg vallen.
[ Bericht 42% gewijzigd door Physics op 15-10-2011 19:19:04 ]
Beschouw de nutsfunctie u(x, y) = min{4x, 3y + 2}. Bereken u′y(1, 1)
Waarom is het u′y(1, 1) = 0 en niet 1?
Soortgelijke vraag van pagina 9:
Waarom is het u′y(1, 1) = 0 en niet 1?
Soortgelijke vraag van pagina 9:
quote:
u(x, y) = min{2x, y}, bepaal u'y(8, 20).
u'y(8, 20) = 0 (volgens de uitwerkingen)
Moet dit niet u'y(8, 20) = 1 zijn?
Dit is het antwoord van een tentamen van vorig jaar, dus ik kan me niet voorstellen dat het fout is.quote:
Mijn vorige antwoord was fout 
min{2x,y} geeft de kleinste van 2x en y, voor (x,y) = (8,20) geeft hij dus 16; de 2x is actief daar, dus de afgeleide naar y is 0.
min{2x,y} geeft de kleinste van 2x en y, voor (x,y) = (8,20) geeft hij dus 16; de 2x is actief daar, dus de afgeleide naar y is 0.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Beschouw de nutsfunctie u(x, y) = min{5x, 6y + 2}. Bereken u′y(3, 2)
5x > 6y+2, dan u′y(3, 2) = 6
5x < 6y+2, dan u′y(3, 2) = 0
5.3 = 15
6.2 + 2 = 14
15 > 14
u′y(3, 2) = 6
Redeneer ik zo goed?
5x > 6y+2, dan u′y(3, 2) = 6
5x < 6y+2, dan u′y(3, 2) = 0
5.3 = 15
6.2 + 2 = 14
15 > 14
u′y(3, 2) = 6
Redeneer ik zo goed?
ja; en u′y(4, 3) is niet gedefinieerd.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dat je hier 5x = 6y+2 mist.quote:
5x > 6y+2, dan u′y(3, 2) = 6
5x < 6y+2, dan u′y(3, 2) = 0
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Niet echt een wiskunde vraag, maar ik denk dat ik hier de beste antwoorden krijg :p
In de opgave staat:
....reduce sales prices by only 2.5% instead of 4%
"The cost of goods sold as a percentage of revenue would change proportionally with the price change."
Toen de price change nog 4% was, was de COGS 57.5% van Sales.
Hoeveel % is de COGS nu van Sales?
*Ik dacht zelf 0,975/0,96 * 0,575*
In de opgave staat:
....reduce sales prices by only 2.5% instead of 4%
"The cost of goods sold as a percentage of revenue would change proportionally with the price change."
Toen de price change nog 4% was, was de COGS 57.5% van Sales.
Hoeveel % is de COGS nu van Sales?
*Ik dacht zelf 0,975/0,96 * 0,575*
Dag allemaal. Ik heb nu het vak hogere wiskunde (wo) en ik vind het echt zooooo moeilijk. 
Ik doe echt mijn best maar bijvoorbeeld onderstaande opgave: ik weet gewoon niet goed waar ik moet beginnen...
Ik doe echt mijn best maar bijvoorbeeld onderstaande opgave: ik weet gewoon niet goed waar ik moet beginnen...Ik begrijp steeds wel het idee van wat er moet gebeuren, maar de notatie is zo ingewikkeld. Ik zou graag iets hebben wat ik goed begreep waar ik kon beginnen. Kan iemand me helpen met het beter begrijpen van bijvoorbeeld het onderwerp "limieten van rijen" zoals bij de opgave hierboven?quote:Veronderstel daten
convergente rijen zijn in
.
Noteeren
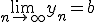
opgave
Doe een voorstel voor de limiet van de rijen bewijs je voorstel m.b.v. de definitie van de limiet van een rij.
definitie limiet van een rij
We zeggen dat een rijin
convergeert naar een
als:
We noemende limiet van de rij
Ze keek me smerig aan ik vond 'm zelf nog zo subtiel
maar ze kon ze niet waarderen, grappen over Tsjernobyl
maar ze kon ze niet waarderen, grappen over Tsjernobyl
Als je de notatie ingewikkeld vindt: probeer het eens (deels) in woorden op te schrijven. Als je het snapt dan stap je waarschijnlijk snel weer over op de wiskundige notatie want dat scheelt een hoop schrijfwerk en maakt het een stuk overzichtelijker.quote:
Dag allemaal. Ik heb nu het vak hogere wiskunde (wo) en ik vind het echt zooooo moeilijk.
[..]
Ik begrijp steeds wel het idee van wat er moet gebeuren, maar de notatie is zo ingewikkeld. Ik zou graag iets hebben wat ik goed begreep waar ik kon beginnen. Kan iemand me helpen met het beter begrijpen van bijvoorbeeld het onderwerp "limieten van rijen" zoals bij de opgave hierboven?
Snap je waar die definitie van de limiet vandaan komt? Zie je een beetje voor je wat er gebeurt, of vind je het maar vaag?
Ik moet zeggen dat ik haar zijn notatie van een rij ook niet helemaal vat, wat betekent (3xn - 2)n?quote:
[..]
Als je de notatie ingewikkeld vindt: probeer het eens (deels) in woorden op te schrijven. Als je het snapt dan stap je waarschijnlijk snel weer over op de wiskundige notatie want dat scheelt een hoop schrijfwerk en maakt het een stuk overzichtelijker.
Snap je waar die definitie van de limiet vandaan komt? Zie je een beetje voor je wat er gebeurt, of vind je het maar vaag?
Beneath the gold, bitter steel
Dat is best normale notatie. Het betekent:quote:
[..]
Ik moet zeggen dat ik haar notatie van een rij ook niet helemaal vat, wat betekent (3xn - 2)n?
3x1-2, 3x2-2 , ...
Het is dus gewoon de rij met n=1, n=2, ...
[ Bericht 2% gewijzigd door thenxero op 17-10-2011 19:54:11 ]
COGS = kosten / omzet * 100%quote:
Niet echt een wiskunde vraag, maar ik denk dat ik hier de beste antwoorden krijg :p
In de opgave staat:
....reduce sales prices by only 2.5% instead of 4%
"The cost of goods sold as a percentage of revenue would change proportionally with the price change."
Toen de price change nog 4% was, was de COGS 57.5% van Sales.
Hoeveel % is de COGS nu van Sales?
*Ik dacht zelf 0,975/0,96 * 0,575*
De kosten blijven gelijk, de prijs en dus de omzet stijgt met een factor 0.975/0.96 dus de COGS stijgen met een factor 0.96/0.975.
Dus ik zou zeggen 0,96/0,975 * 0,575.
Aha, dat klopt volgens het antwoordmodel inderdaad. thxquote:
[..]
COGS = kosten / omzet * 100%
De kosten blijven gelijk, de prijs en dus de omzet stijgt met een factor 0.975/0.96 dus de COGS stijgen met een factor 0.96/0.975.
Dus ik zou zeggen 0,96/0,975 * 0,575.
Je bent de notatie van een rij met accolades gewend? Of ken je die ook niet?quote:
[..]
Ik moet zeggen dat ik haar zijn notatie van een rij ook niet helemaal vat, wat betekent (3xn - 2)n?
Die inderdaad, of gewoon als an = 3n - 2quote:
[..]
Je bent de notatie van een rij met accolades gewend? Of ken je die ook niet?
Beneath the gold, bitter steel
Subtiel verschil: an = 3n - 2 is een element van de rij, en niet de rij zelfquote:
[..]
Die inderdaad, of gewoon als an = 3n - 2
.
De definitie voor een limiet van een rij is nauw verwant met de bekende ε,δ definitie van een limiet van een functie. Begin even met dit door te nemen. Het gebruik van kwantoren maakt de notatie van de definitie compacter en overzichtelijker. De definitie voor een limiet L van een rij (an) of {an} is niets meer dan een formalisering van wat je je hier intuïtief bij voorstelt, namelijk dat je an zo dicht tegen L kunt laten aankruipen als je zelf wil als je n maar groot genoeg kiest.quote:
Dag allemaal. Ik heb nu het vak hogere wiskunde (wo) en ik vind het echt zooooo moeilijk.
[..]
Ik begrijp steeds wel het idee van wat er moet gebeuren, maar de notatie is zo ingewikkeld. Ik zou graag iets hebben wat ik goed begreep waar ik kon beginnen. Kan iemand me helpen met het beter begrijpen van bijvoorbeeld het onderwerp "limieten van rijen" zoals bij de opgave hierboven?
Vind je het correct als ik erachter had gehad n element uit {natuurlijke getallen} ?quote:
[..]
Subtiel verschil: an = 3n - 2 is een element van de rij, en niet de rij zelf
In het boek werd het altijd zo of met accolades gegeven dacht ik.
Ik moet zeggen dat ik wel altijd rijen en reeksen door elkaar haalde, omdat mensen ze vaak door elkaar gebruiken.
Beneath the gold, bitter steel
Dan is het nog steeds een element uit de rij en niet de rij zelf. Als je echt naar de rij wil refereren met die formule dan zou ik het formuleren als: "de rij die gegeven wordt door an = 3n - 2 (met n in N)".
(ik moet toegeven dat het wel een beetje mierenneuken is)
(ik moet toegeven dat het wel een beetje mierenneuken is)
Ah, bedankt. Ik ben nu de wiki pagina's aan het doornemen en zal morgen hier nog even terugkomen met wat ik ervan begrijpquote:
[..]
De definitie voor een limiet van een rij is nauw verwant met de bekende ε,δ definitie van een limiet van een functie. Begin even met dit door te nemen. Het gebruik van kwantoren maakt de notatie van de definitie compacter en overzichtelijker. De definitie voor een limiet L van een rij (an) of {an} is niets meer dan een formalisering van wat je je hier intuïtief bij voorstelt, namelijk dat je an zo dicht tegen L kunt laten aankruipen als je zelf wil als je n maar groot genoeg kiest.
Maar wat ik ook niet zo goed begrijp aan de hele notatie is het kommagebruik.Ik snap wel dat je bijvoorbeeld zegt:
(voor elk kind (k) bestaat er precies 1 moeder (v).
Maar in de omschrijving:
is me dit al een stuk minder duidelijk. Ik vind het moeilijk om dit "onder woorden te brengen" zegmaar...
Ze keek me smerig aan ik vond 'm zelf nog zo subtiel
maar ze kon ze niet waarderen, grappen over Tsjernobyl
maar ze kon ze niet waarderen, grappen over Tsjernobyl
Je kan het lezen als:quote:
[..]
Ah, bedankt. Ik ben nu de wiki pagina's aan het doornemen en zal morgen hier nog even terugkomen met wat ik ervan begrijp
Ik snap wel dat je bijvoorbeeld zegt:
(voor elk kind (k) bestaat er precies 1 moeder (v).
Maar in de omschrijving:
is me dit al een stuk minder duidelijk. Ik vind het moeilijk om dit "onder woorden te brengen" zegmaar...
Voor iedere epsilon groter dan 0 bestaat er een natuurlijk getal k0 zodat als k groter of gelijk is aan k0, dan is de afstand tussen xk en a kleiner dan epsilon.
Okequote:
[..]
Je kan het lezen als:
Voor iedere epsilon groter dan 0 bestaat er een natuurlijk getal k0 zodat als k groter of gelijk is aan k0, dan is de afstand tussen xk en a kleiner dan epsilon.
en waar is dan het stukje na de laatste komma? dus:want ik begrijp inderdaad: Voor "eerste stuk" bestaat "tweede stuk" zodat "achter dubbele punt"
Maar het "derde stuk" lijk ik dan te missen...
Ze keek me smerig aan ik vond 'm zelf nog zo subtiel
maar ze kon ze niet waarderen, grappen over Tsjernobyl
maar ze kon ze niet waarderen, grappen over Tsjernobyl
Daarmee geef je eigenlijk alleen nog aan dat k een natuurlijk getal is. Wat er gebeurt is het volgende: eerst neem je k als een willekeurig natuurlijk getal. Dan zeg je als hij groot genoeg is, dan geldt een bepaalde ongelijkheid. (een beetje omslachtig maar wel correct).
Ik vind het zelf mooier om het zo neer te zetten, al is het equivalent met jouw uitspraak:
Laat k0 en k natuurlijke getallen zijn en epsilon reëel. Dan is per definitie de limiet van xk gelijk aan a dan en slechts dan als
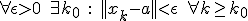
of eventueel
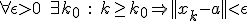
Snap je waarom dat allemaal hetzelfde is?
Ik vind het zelf mooier om het zo neer te zetten, al is het equivalent met jouw uitspraak:
Laat k0 en k natuurlijke getallen zijn en epsilon reëel. Dan is per definitie de limiet van xk gelijk aan a dan en slechts dan als
of eventueel
Snap je waarom dat allemaal hetzelfde is?
Dat is weliswaar wat beter te verteren dan drie kwantoren achter elkaar, maar formeel (syntactisch) is de eerste regel niet juist omdat je na ∀k≥k₀ een uitspraak verwacht.quote:
Daarmee geef je eigenlijk alleen nog aan dat k een natuurlijk getal is. Wat er gebeurt is het volgende: eerst neem je k als een willekeurig natuurlijk getal. Dan zeg je als hij groot genoeg is, dan geldt een bepaalde ongelijkheid. (een beetje omslachtig maar wel correct).
Ik vind het zelf mooier om het zo neer te zetten, al is het equivalent met jouw uitspraak:
Laat k0 en k natuurlijke getallen zijn en epsilon reëel. Dan is per definitie de limiet van xk gelijk aan a dan en slechts dan als
of eventueel
Snap je waarom dat allemaal hetzelfde is?
Je hebt gelijk, het is wel inzichtelijker alleen formeel misschien niet zo netjes. Die tweede is wat netter.quote:
[..]
Dat is weliswaar wat beter te verteren dan drie kwantoren achter elkaar, maar formeel (syntactisch) is het niet juist omdat je na ∀k≥k₀ een uitspraak verwacht.
Een kleine vraag over een definitie:
Kan de afgeleide f' van een functie f een groter domein hebben dan de functie f zelf?
Een concreet voorbeeld:
Zeg je dat f'(x) = 1/x een groter domein heeft dan f(x)=log(x)?
Kan de afgeleide f' van een functie f een groter domein hebben dan de functie f zelf?
Een concreet voorbeeld:
Zeg je dat f'(x) = 1/x een groter domein heeft dan f(x)=log(x)?
Finally, someone let me out of my cage
Nee, kijk maar naar de definitie van de afgeleide: daar heb je toch echt de functiewaardes nodig en daar moet de functie dus wel gedefinieerd zijn.
De afgeleide van f:R naar R gedefinieerd door f(x) = log( |x| ) is f'(x)=1/x op heel R. Maar de afgeleide van g:R+ naar R, g(x) = log(x) is g' : R+ naar R, g'(x)=1/x.
De afgeleide van f:R naar R gedefinieerd door f(x) = log( |x| ) is f'(x)=1/x op heel R. Maar de afgeleide van g:R+ naar R, g(x) = log(x) is g' : R+ naar R, g'(x)=1/x.
Ik zou zeggen van niet omdat f'(x) is gedefinieerd als de limiet voor h → 0 van het differentiequotiënt (f(x+h)-f(x))/h en die limiet kan niet zijn gedefinieerd als f(x) niet is gedefinieerd. Je kunt hier wel zeggen dat f'(x) = 1/x de afgeleide is van f(x) = log |x| en dan kun je het domein van beide oprekken tot R\{0}.quote:
Een kleine vraag over een definitie:
Kan de afgeleide f' van een functie f een groter domein hebben dan de functie f zelf?
Een concreet voorbeeld:
Zeg je dat f'(x) = 1/x een groter domein heeft dan f(x)=log(x)?
Minibeer, bij jouw voorbeeldt geldt f'(x) = 1/x alleen voor x>0.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
quote:
Nee, kijk maar naar de definitie van de afgeleide: daar heb je toch echt de functiewaardes nodig en daar moet de functie dus wel gedefinieerd zijn.
De afgeleide van f:R naar R gedefinieerd door f(x) = log( |x| ) is f'(x)=1/x op heel R. Maar de afgeleide van g:R+ naar R, g(x) = log(x) is g' : R+ naar R, g'(x)=1/x.
quote:
[..]
Ik zou zeggen van niet omdat f'(x) is gedefinieerd als de limiet voor h → 0 van het differentiequotiënt (f(x+h)-f(x))/h en die limiet kan niet zijn gedefinieerd als f(x) niet is gedefinieerd. Je kunt hier wel zeggen dat f'(x) = 1/x de afgeleide is van f(x) = log |x| en dan kun je het domein van beide oprekken tot R\{0}.
Ok, dat is ook wel zo logisch jaquote:
Minibeer, bij jouw voorbeeldt geldt f'(x) = 1/x alleen voor x>0.
Danks!
Finally, someone let me out of my cage
Vrij irritant die oefententamens die makkelijker zijn dan echte tentamens.. Voor deze had ik een 10 kunnen halen maar de echte is sowieso een stuk moeilijker, als ik de trial exams met de echte vergelijk was het vorige jaren ook zo..
Van wat?quote:
Vrij irritant die oefententamens die makkelijker zijn dan echte tentamens.. Voor deze had ik een 10 kunnen halen maar de echte is sowieso een stuk moeilijker, als ik de trial exams met de echte vergelijk was het vorige jaren ook zo..
O(t) = 0,5*2t
Geef de differentiaalvergelijking die bij dit model hoort.
O'(t) =
Iemand die me op weg kan helpen?
Geef de differentiaalvergelijking die bij dit model hoort.
O'(t) =
Iemand die me op weg kan helpen?
