GC General Chat
Hier kun je praten over van alles en nog wat. Eigenlijk alles wat niet in een van de andere rubrieken thuishoort.



Dat het getalsmatig niet uit te drukken valt betekent niet dat het niet kan!quote:Op zaterdag 9 april 2011 08:46 schreef hello_moto1992 het volgende:
Dan is elk stuk 0.(...)33etc. en heb je 0.(...)01 over
Op dinsdag 21 februari 2012 22:30 schreef JoanFranka het volgende:
PINGUINS RULEREN!! Dat zijn echt een van de grappigste dieren op aarde hahahaa
PINGUINS RULEREN!! Dat zijn echt een van de grappigste dieren op aarde hahahaa


Denken dat het percentage er iets mee te maken heeft 
stel die taart weegt 99 gram
1x 33 gram
1x 33 gram
1x 33 gram
aub, hier heb je je drie stukken,
tyfusmongooltje
stel die taart weegt 99 gram
1x 33 gram
1x 33 gram
1x 33 gram
aub, hier heb je je drie stukken,
tyfusmongooltje


Maar hij weegt 100 gramquote:Op zaterdag 9 april 2011 08:53 schreef LindstrÝm. het volgende:
Denken dat het percentage er iets mee te maken heeft
stel die taart weegt 99 gram
1x 33 gram
1x 33 gram
1x 33 gram
aub, hier heb je je drie stukken,
tyfusmongooltje


SES? ONZ lijkt me meer op zijn plaats...quote:Op zaterdag 9 april 2011 08:57 schreef LindstrÝm. het volgende:
wat doet deze hoge wiskunde in CG btwop naar SES


Om het dus samen te vatten.quote:Op zaterdag 9 april 2011 08:56 schreef LindstrÝm. het volgende:
[..]
nou dan weegt elk stuk 33 1/3 gram
1x 33 1/3 gram
1x 33 1/3 gram
1x 33 1/3 gram
= 100 gram
aub
Elk deel taart weegt 1/3 van het totaal gewicht minus de kruimels en reststukken die op het mes en de verpakking blijven zitten.
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.


Leg uit!quote:Op zaterdag 9 april 2011 08:47 schreef Pheno het volgende:
[..]
Dat het getalsmatig niet uit te drukken valt betekent niet dat het niet kan!


quote:Op zaterdag 9 april 2011 08:57 schreef Slurf het volgende:
[..]
SES? ONZ lijkt me meer op zijn plaats...


Betere vraag: kan je visite nagaan of ze exact 1/3e stuk taart hebben ontvangen?
My heart is broke
May I have some glue?
Help me inhale
And mend it with you
May I have some glue?
Help me inhale
And mend it with you


Nee. Gaat het dan om het oppervlakte, inhoud of gewicht? Er zijn meerdere dingen waardoor je hem in drieŽn kan delen. Zolang je dat niet weet kan je het ook niet weten of je 1/3 hebt.quote:Op zaterdag 9 april 2011 09:02 schreef Transport_Ink het volgende:
Betere vraag: kan je visite nagaan of ze exact 1/3e stuk taart hebben ontvangen?
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.


Als dit allemaal te moeilijk is voor je, kun je wellicht beter drie eenpersoonstaartjes kopen bij de bakker.quote:


ik ga van een volledig symmetrische taart uit.quote:Op zaterdag 9 april 2011 09:04 schreef kanovinnie het volgende:
[..]
Nee. Gaat het dan om het oppervlakte, inhoud of gewicht? Er zijn meerdere dingen waardoor je hem in drieŽn kan delen. Zolang je dat niet weet kan je het ook niet weten of je 1/3 hebt.


volgens mij snap je niet helemaal wat ik bedoelquote:Op zaterdag 9 april 2011 09:04 schreef kwiwi het volgende:
[..]
Als dit allemaal te moeilijk is voor je, kun je wellicht beter drie eenpersoonstaartjes kopen bij de bakker.


Symmetrisch over 3 assen? Anders gaat 't nog steeds niet werken.quote:Op zaterdag 9 april 2011 09:05 schreef hello_moto1992 het volgende:
[..]
ik ga van een volledig symmetrische taart uit.
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.


je hebt geen 3zijdige symmetriequote:Op zaterdag 9 april 2011 09:09 schreef kanovinnie het volgende:
[..]
Symmetrisch over 3 assen? Anders gaat 't nog steeds niet werken.


Wordt een lange verjaardag, ik zie het alquote:Op zaterdag 9 april 2011 09:04 schreef kanovinnie het volgende:
[..]
Nee. Gaat het dan om het oppervlakte, inhoud of gewicht? Er zijn meerdere dingen waardoor je hem in drieŽn kan delen. Zolang je dat niet weet kan je het ook niet weten of je 1/3 hebt.
My heart is broke
May I have some glue?
Help me inhale
And mend it with you
May I have some glue?
Help me inhale
And mend it with you


joahquote:Op zaterdag 9 april 2011 09:09 schreef kanovinnie het volgende:
[..]
Symmetrisch over 3 assen? Anders gaat 't nog steeds niet werken.


Ik snap het wel hoor, maar het antwoord is al gegeven, en verder is het zo'n onzinnig topic dat je ook een bijpassend antwoord van me kreegquote:Op zaterdag 9 april 2011 09:06 schreef hello_moto1992 het volgende:
[..]
volgens mij snap je niet helemaal wat ik bedoel
Nederduitse/Mevrouw qltel


Gewoon horizontaal in drieŽn verdelen. Probleem opgelost.
Most people don't listen with the intention to understand, they listen with the intention to reply.
<a href="http://bijenzonderzorgen.nl/" target="_blank" rel="nofollow">http://bijenzonderzorgen.nl/</a> beslist geen BIJ-zaak!
<a href="http://bijenzonderzorgen.nl/" target="_blank" rel="nofollow">http://bijenzonderzorgen.nl/</a> beslist geen BIJ-zaak!


maar dan zijn ze niet even groot.quote:Op zaterdag 9 april 2011 09:13 schreef Rewimo het volgende:
Gewoon horizontaal in drieŽn verdelen. Probleem opgelost.


Met een mes. En dan in drie gelijke stukken verdelen. Klaar. Opgelost. Graag gedaan.quote:
F.K.A. SuperwormJim


ik snap de denkwijze overigens wel
100% = taart
gedeeld door 3 = 33,33% = "kan niet"
zelfde verhaal als 2 keer de helft.
100% van wat? van het gewicht (100gram)
uitdrukkingen als 'procent' en 'helft' moeten altijd gelinkt zijn aan een grootheid, anders zegt het inderdaad niks over de hoeveelheid.
NU DUIDELIJK KLAPMONGOOLTJES?
100% = taart
gedeeld door 3 = 33,33% = "kan niet"
zelfde verhaal als 2 keer de helft.
100% van wat? van het gewicht (100gram)
uitdrukkingen als 'procent' en 'helft' moeten altijd gelinkt zijn aan een grootheid, anders zegt het inderdaad niks over de hoeveelheid.
NU DUIDELIJK KLAPMONGOOLTJES?


Vanuit gaande dat het gewicht evenredig in de taart is verdeeld.quote:Op zaterdag 9 april 2011 08:56 schreef LindstrÝm. het volgende:
[..]
nou dan weegt elk stuk 33 1/3 gram
1x 33 1/3 gram
1x 33 1/3 gram
1x 33 1/3 gram
= 100 gram
aub


trappen in dit trolltopicquote:Op zaterdag 9 april 2011 09:16 schreef LindstrÝm. het volgende:
ik snap de denkwijze overigens wel
100% = taart
gedeeld door 3 = 33,33% = "kan niet"
zelfde verhaal als 2 keer de helft.
100% van wat? van het gewicht (100gram)
uitdrukkingen als 'procent' en 'helft' moeten altijd gelinkt zijn aan een grootheid, anders zegt het inderdaad niks over de hoeveelheid.
NU DUIDELIJK KLAPMONGOOLTJES?


moet je even kijken naar de aardbeien op de taart.. als het ene stuk 3 aardbeien heeft en die andere 2 per stuk tsja dan kan het niet meer iddquote:Op zaterdag 9 april 2011 09:16 schreef Pakspul het volgende:
[..]
Vanuit gaande dat het gewicht evenredig in de taart is verdeeld.


Dan nog moet alles perfect verdeelt zijn omdat het anders niet klopt. Dan heeft iemand meer oppervlakte, gewicht of inhoud.quote:Op zaterdag 9 april 2011 09:18 schreef Ajacied422 het volgende:
vergeet die aardbeien, we hebben het gewoon over een appeltaart
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.


Whehe, komt dat kutkind echt uit '92? dan zou die op zijn minst al 18 moeten zijn.. zucht.. 1/3 van 18 is meer op zijn plaatsquote:


Wat zij zegt!quote:Op zaterdag 9 april 2011 09:13 schreef Rewimo het volgende:
Gewoon horizontaal in drieŽn verdelen. Probleem opgelost.
En verder: OMG


kan niet,quote:
als je een taart horinzontaal verdeelt, dan zijn de stukjes met de onderkanten kleiner dan de middelste, die heeft een langwerpig en breed oppervlak


• Je kan het teweten komen door het gewicht van de taart te weten
• Je kan het met de omtrek berekenen, Dan komt de PI, straal en diameter aan bod
Er zijn dus verschillende theorien om er achter te komen,
• Je kan het met de omtrek berekenen, Dan komt de PI, straal en diameter aan bod
Er zijn dus verschillende theorien om er achter te komen,


Je kunt de repeterende breuk, die driedeling onmogelijk lijkt te maken (lijkt, want onmogelijk is het niet) omzeilen in het geval van een ronde taart door hoeken van 120 graden te construeren.


Ja het kan: (even met paint gemaakt: rood zijn de snijlijnen, blauw zijn hulplijnen)
Je snijdt dus ergens in tot aan het midden. Dan bedenk je vervolgens hoe de lijn verder loopt. Dit verdere verloop deel je in twee gelijke stukken. Vervolgens kijk je waar de lijn die 90 graden op de andere lijn staat en door het middelpunt van de hulplijn gaat, de cirkel snijdt. Als je vanaf die punten een snee maakt naar het middelpunt heb je drie gelijke stukken.
Je snijdt dus ergens in tot aan het midden. Dan bedenk je vervolgens hoe de lijn verder loopt. Dit verdere verloop deel je in twee gelijke stukken. Vervolgens kijk je waar de lijn die 90 graden op de andere lijn staat en door het middelpunt van de hulplijn gaat, de cirkel snijdt. Als je vanaf die punten een snee maakt naar het middelpunt heb je drie gelijke stukken.
HJ 14-punt-gift.
Lijst met rukmateriaal!
Lijst met rukmateriaal!


Als alle stukken 33 1/3 gram wegen maakt dat niets uit.quote:Op zaterdag 9 april 2011 09:16 schreef Pakspul het volgende:
[..]
Vanuit gaande dat het gewicht evenredig in de taart is verdeeld.
Op donderdag 2 juli 2009 22:41 schreef RTB het volgende:
als ik elk rap"liedje" een kans moest geven was ik aan het eind van dit millennium nog bezig met het tempo waarin die kotshoop uitgebraakt wordt.
👾
als ik elk rap"liedje" een kans moest geven was ik aan het eind van dit millennium nog bezig met het tempo waarin die kotshoop uitgebraakt wordt.
👾


Dan maakt het niet uit neequote:Op zaterdag 9 april 2011 10:04 schreef mstx het volgende:
[..]
Als alle stukken 33 1/3 gram wegen maakt dat niets uit.
Maar in de praktijk is het eigenlijk niet te doen, mits je gaat afronden. Sommige breuken kun je in de werkelijkheid niet maken omdat ze oneindig zijn.


Je kent het fabelachtige fenomeen 1/3 niet?quote:Op zaterdag 9 april 2011 09:06 schreef hello_moto1992 het volgende:
[..]
volgens mij snap je niet helemaal wat ik bedoel
Wat die wetenschappers ook allemaal bedenken he.
Ik in een aantal worden omschreven: Ondernemend | Moedig | Stout | Lief | Positief | IntuÔtief | Communicatief | Humor | Creatief | Spontaan | Open | Sociaal | Vrolijk | Organisator | Pro-actief | Meedenkend | Levensgenieter | Spiritueel


Het is mooi weer, dus sommige FOK!users vervelen zich dan en openen dit soort topics.quote:Op zaterdag 9 april 2011 10:26 schreef eleusis het volgende:
[..]
Je kent het fabelachtige fenomeen 1/3 niet?
Wat die wetenschappers ook allemaal bedenken he.
Op dinsdag 21 februari 2012 22:30 schreef JoanFranka het volgende:
PINGUINS RULEREN!! Dat zijn echt een van de grappigste dieren op aarde hahahaa
PINGUINS RULEREN!! Dat zijn echt een van de grappigste dieren op aarde hahahaa


En dat is niet waar. Stel dat een bakker drie identieke taarten heeft, en je wil daar 1/3 van kopen, dan is dat exact 1 taart.quote:Op zaterdag 9 april 2011 10:13 schreef Pakspul het volgende:
Maar in de praktijk is het eigenlijk niet te doen, mits je gaat afronden. Sommige breuken kun je in de werkelijkheid niet maken omdat ze oneindig zijn.


Maar als hij 2 taarten heeft, dan krijg je 3 stukken van 2/3. Dus dan zou je een stuk van 0,(oneindig veel zessen)6 krijgen. Dan blijft er altijd 0,(oneindig veel nullen)2 over.quote:Op zaterdag 9 april 2011 11:18 schreef ..-._---_-.- het volgende:
[..]
En dat is niet waar. Stel dat een bakker drie identieke taarten heeft, en je wil daar 1/3 van kopen, dan is dat exact 1 taart.


Als je nu 2 taarten van 300 gram each hebt.. dan heb je plots wel weer een heel getal. Krijg je potdikkeme gewoon 200 gram taart! lekker hoor.quote:Op zaterdag 9 april 2011 11:26 schreef hello_moto1992 het volgende:
[..]
Maar als hij 2 taarten heeft, dan krijg je 3 stukken van 2/3. Dus dan zou je een stuk van 0,(oneindig veel zessen)6 krijgen. Dan blijft er altijd 0,(oneindig veel nullen)2 over.
Je kan dus prima taarten in 3en delen.


Oneindig veel nullen = niets = FTW.quote:Op zaterdag 9 april 2011 11:26 schreef hello_moto1992 het volgende:
[..]
Maar als hij 2 taarten heeft, dan krijg je 3 stukken van 2/3. Dus dan zou je een stuk van 0,(oneindig veel zessen)6 krijgen. Dan blijft er altijd 0,(oneindig veel nullen)2 over.
Ik in een aantal worden omschreven: Ondernemend | Moedig | Stout | Lief | Positief | IntuÔtief | Communicatief | Humor | Creatief | Spontaan | Open | Sociaal | Vrolijk | Organisator | Pro-actief | Meedenkend | Levensgenieter | Spiritueel


Jezus Christus, leren de kinderen tegenwoordig alleen maar om toetsjes in te drukken van hun rekenmachine ofzo? 


Dat TS gewoon 3 taarten koopt....
- I'm buttwalking... is that a crime? -
-Never underestimate the predictability of stupidity-
-Never underestimate the predictability of stupidity-


Mercedes-Benz.quote:Op zaterdag 9 april 2011 08:44 schreef Viking84 het volgende:
Waarom niet? Tuurlijk wel. Zoals een Mercedeslogo:
[ afbeelding ]


Goeie. Die moet ik onthouden.quote:Op zaterdag 9 april 2011 10:02 schreef freiss het volgende:
Ja het kan: (even met paint gemaakt: rood zijn de snijlijnen, blauw zijn hulplijnen)
[ afbeelding ]
Je snijdt dus ergens in tot aan het midden. Dan bedenk je vervolgens hoe de lijn verder loopt. Dit verdere verloop deel je in twee gelijke stukken. Vervolgens kijk je waar de lijn die 90 graden op de andere lijn staat en door het middelpunt van de hulplijn gaat, de cirkel snijdt. Als je vanaf die punten een snee maakt naar het middelpunt heb je drie gelijke stukken.


Wat dan, blijft er een Higgs-Boson achter ofzo als je hem in drieŽn deelt?
Hoi, ik ben een lamzak met een passie voor flessen wasverzachter.
Neuk mijn oor en noem me Harry Mulisch
Neuk mijn oor en noem me Harry Mulisch


Dus je wil zeggen dat je dingen echt in drie delen kunt delen? Vindt dat erg ongeloofwaardig hoor.quote:Op zaterdag 9 april 2011 10:26 schreef eleusis het volgende:
[..]
Je kent het fabelachtige fenomeen 1/3 niet?
Wat die wetenschappers ook allemaal bedenken he.


TS heeft maar 3 vrienden ( die taart lusten)
You have to make the right choice. As long as you don't choose, everything remains possible.


quote:Op zaterdag 9 april 2011 13:29 schreef Granduppaaaaah het volgende:
Volgens mij hou je altijd een stukje over als je het in drie delen probeert te delen.
Deel het volgende in drieŽn:
aaa
Resultaat:
a en a en a.
Er blijft niets over.
De fout die hier constant gemaakt wordt, is dat een derde geen absoluut getal is, maar slechts een factor.
[ Bericht 8% gewijzigd door Dastan op 09-04-2011 17:48:47 ]


Ze kunnen nooit alle 3 precies even groot zijn 
Op 31-12-2010 20:01 schreef ViezeFreddiey
meest baas van FoK 2010 _O_
meest baas van FoK 2010 _O_


Jawel.quote:Op zaterdag 9 april 2011 17:49 schreef willemwaus het volgende:
Ze kunnen nooit alle 3 precies even groot zijn
quote:Op zaterdag 9 april 2011 17:27 schreef Dastan het volgende:
De fout die hier constant gemaakt wordt, is dat een derde geen absoluut getal is, maar slechts een factor.


Je houd altijd 0.0000miljardhonderste of tot hoever je wilt gaan001 over.quote:
Op 31-12-2010 20:01 schreef ViezeFreddiey
meest baas van FoK 2010 _O_
meest baas van FoK 2010 _O_


Waarom?quote:Op zaterdag 9 april 2011 17:51 schreef willemwaus het volgende:
[..]
Je houd altijd 0.0000miljardhonderste of tot hoever je wilt gaan001 over.
Stel dit is de taart:
####
####
####
Je wilt hem in drieŽn delen. Dan snijd je zo dat voor elk stuk geldt: ####. Dan houd je toch niets over?


Een driehoekige taart wel. Die kun je gewoon twee keer door de helft snijden en dan heeft iedereen evenveel, want dan blijven er ook geen kruimels achter.


quote:Op zaterdag 9 april 2011 10:02 schreef freiss het volgende:
Ja het kan: (even met paint gemaakt: rood zijn de snijlijnen, blauw zijn hulplijnen)
[ afbeelding ]
Je snijdt dus ergens in tot aan het midden. Dan bedenk je vervolgens hoe de lijn verder loopt. Dit verdere verloop deel je in twee gelijke stukken. Vervolgens kijk je waar de lijn die 90 graden op de andere lijn staat en door het middelpunt van de hulplijn gaat, de cirkel snijdt. Als je vanaf die punten een snee maakt naar het middelpunt heb je drie gelijke stukken.


0.50 x 0.50 x 0.50?quote:
Dat is wel een hele lullige taart
- I'm buttwalking... is that a crime? -
-Never underestimate the predictability of stupidity-
-Never underestimate the predictability of stupidity-


definieer "absoluut getal".quote:Op zaterdag 9 april 2011 17:27 schreef Dastan het volgende:
[..]
Deel het volgende in drieŽn:
aaa
Resultaat:
a en a en a.
Er blijft niets over.
De fout die hier constant gemaakt wordt, is dat een derde geen absoluut getal is, maar slechts een factor.
"Ik quote graag mezelf."


waar TS waarschijnlijk onbewust mee in de war is zijn passer en liniaal constructies. Kan je een cirkel in 3 gelijke stukken delen met een passer en liniaal. Het antwoord is ja.
"Ik quote graag mezelf."


het heeft geen eindige decimale reeksontwikkeling, klopt, maar dat is iets anders dan absoluut getalquote:Op zaterdag 9 april 2011 19:02 schreef Dastan het volgende:
[..]
Dat 'een derde' niet het getal 1/3 = 0,333...3 is,
"Ik quote graag mezelf."


Hoezo? Ik bedoelde te zeggen dat 'een derde' niet onveranderlijk is (absoluut), maar relatief. Het zegt immers iets over het aantal waarmee het vermenigvuldigd wordt. Een factor dus.quote:Op zaterdag 9 april 2011 19:04 schreef San_Andreas het volgende:
[..]
het heeft geen eindige decimale reeksontwikkeling, klopt, maar dat is iets anders dan absoluut getal


definieer relatieve en onveranderlijke getallenquote:Op zaterdag 9 april 2011 19:09 schreef Dastan het volgende:
[..]
Hoezo? Ik bedoelde te zeggen dat 'een derde' niet onveranderlijk is (absoluut), maar relatief. Het zegt immers iets over het aantal waarmee het vermenigvuldigd wordt. Een factor dus.
een getal op zich zegt niks over vermenigvuldigen
"Ik quote graag mezelf."


Nou ja, ik sprak ook niet in vakjargon natuurlijk. Het spijt me dat ik het niet zo kan verwoorden als ik bedoel. 


Als jullie denken dat door 3 delen moeilijk is, moet je een taart eens 2x door de helft delen. Dat is pas moeilijk.
[b]Op vrijdag 24 augustus 2007 09:50 schreef PretKroket het volgende:[/b]
dude? :') ik hoop voor je dat je niet serieus bent
Even voor jou: 2x1/2 = 1/2 x 1/2
[b]Neem mij niet tŤ serieus, dat doe ik zelf ook niet[/b]
dude? :') ik hoop voor je dat je niet serieus bent
Even voor jou: 2x1/2 = 1/2 x 1/2
[b]Neem mij niet tŤ serieus, dat doe ik zelf ook niet[/b]


Daar kan je hele topics over vullen!quote:Op zaterdag 9 april 2011 19:19 schreef Barcaconia het volgende:
Als jullie denken dat door 3 delen moeilijk is, moet je een taart eens 2x door de helft delen. Dat is pas moeilijk.
Maar hoe deel je dit dan door 3?quote:Op zaterdag 9 april 2011 19:20 schreef Dastan het volgende:
Twee keer door de helft is natuurlijk eenvoudig.
1/(0,5)=2 2/(0,5)=4. Dan heb je vier taarten.
Dat is dan 1 1/3 taart... Dan heb je nog geen eerlijke verdeling!
- I'm buttwalking... is that a crime? -
-Never underestimate the predictability of stupidity-
-Never underestimate the predictability of stupidity-


Goed punt. Als we die nu nog eens maal twee keer de helft doen:quote:Op zaterdag 9 april 2011 20:56 schreef numero_uno het volgende:
[..]
Daar kan je hele topics over vullen!
[..]
Maar hoe deel je dit dan door 3?
Dat is dan 1 1/3 taart... Dan heb je nog geen eerlijke verdeling!
4 * 0,5 + 0,5 = 2,5 En daar die helft van het begin bij optellen krijgen we 2,5 + 0,5 = 3.
3 * 1/3 = 1.


Jezus wat is dit voor een topic? Hoe moeilijk is het om een X getal door drie te delen?
It is our light, not our darkness that frightens us the most.
Our biggest fear is not that we are inadequate, our biggest fear is that we are powerful beyond measure.
Our biggest fear is not that we are inadequate, our biggest fear is that we are powerful beyond measure.


Een ronde taart kun je sowieso niet opdelen in stukken. De omtrek en oppervlak is namelijk afhankelijk van pi, en dat is een irrationeel getal. En met irrationele getallen kun je helemaal niks beginnen.


Deze man weet hetquote:Op zaterdag 9 april 2011 22:17 schreef Dastan het volgende:
[..]
Goed punt. Als we die nu nog eens maal twee keer de helft doen:
4 * 0,5 + 0,5 = 2,5 En daar die helft van het begin bij optellen krijgen we 2,5 + 0,5 = 3.
3 * 1/3 = 1.
|
|


 Op
Op 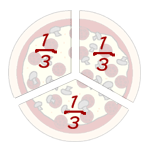


 Op
Op 