[Bèta wiskunde] Huiswerk- en vragentopic.

SES School, Studie en Onderwijs

Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni

Je bent niet ingelogd. Klik hier om in te loggen of hier om een gratis account aan te maken.

actieve topics nieuwe topics

abonnement Unibet Coolblue Bitvavo

actieve topics nieuwe topics

abonnement Unibet Coolblue Bitvavo

dinsdag 7 november 2017 @ 16:01:37 #201

_--_

In varietate concordia

Ik weet wel dit 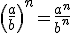$\left(\frac{a}{b}\right)^n=\frac{a^n}{b^n}$ . Maar snap niet zo goed hoe je dat toepast als er nog een minnetje voor staat en een letter tot de macht n.

Crack the following and we will get back to you: !1!llssod000;;

dinsdag 7 november 2017 @ 16:34:17 #202

Janneke141

Green, green grass of home

quote:
Op dinsdag 7 november 2017 16:01 schreef _--_ het volgende:
Ik weet wel dit $\left(\frac{a}{b}\right)^n=\frac{a^n}{b^n}$ . Maar snap niet zo goed hoe je dat toepast als er nog een minnetje voor staat en een letter tot de macht n.

Het minteken zou je kunnen zien als een vermenigvuldiging met -1. en (-1)^5 = -1, dus blijf je een minteken houden.

Had er geen vijfde maar een zesde macht gestaan dan was het minteken verdwenen, aangezien (-1)^6 = 1.

Opinion is the medium between knowledge and ignorance (Plato)

dinsdag 7 november 2017 @ 16:36:18 #203

_--_

In varietate concordia

quote:
Op dinsdag 7 november 2017 16:34 schreef Janneke141 het volgende:

[..]

Het minteken zou je kunnen zien als een vermenigvuldiging met -1. en (-1)^5 = -1, dus blijf je een minteken houden.

Had er geen vijfde maar een zesde macht gestaan dan was het minteken verdwenen, aangezien (-1)^6 = 1.

En die k^2 wordt dus k^10. Dat kan zomaar in de breuk gestopt worden?

Crack the following and we will get back to you: !1!llssod000;;

dinsdag 7 november 2017 @ 16:40:08 #204

Alrac4

quote:
Op dinsdag 7 november 2017 15:51 schreef _--_ het volgende:
$\left(-\frac{2}{3}k^2\right)^5=-\frac{2^5k^{10}}{3^5}$
Wat zijn de tussenstappen hier en waarom?

Je weet ook dat $(a b)^n = a^nb^n$ .
Dus schrijf $-\frac{2}{3}k^2$ als $(-1)\cdot\frac{2}{3}\cdot k^2$
Dan gebruik je de regel voor vermenigvuldigen:
$(-1)^5\cdot(\frac{2}{3})^5\cdot(k^2)^5$
Dan werk je alle losse termen uit:
$(-1)\cdot(\frac{2^5}{3^5})\cdot k^{10}$
En dan combineer je alles weer:
$-\frac{2^5 k^{10}}{3^5}$

dinsdag 7 november 2017 @ 16:45:12 #205

_--_

In varietate concordia

quote:
Op dinsdag 7 november 2017 16:40 schreef Alrac4 het volgende:

[..]

Je weet ook dat $(a b)^n = a^nb^n$ .
Dus schrijf $-\frac{2}{3}k^2$ als $(-1)\cdot\frac{2}{3}\cdot k^2$
Dan gebruik je de regel voor vermenigvuldigen:
$(-1)^5\cdot(\frac{2}{3})^5\cdot(k^2)^5$
Dan werk je alle losse termen uit:
$(-1)\cdot(\frac{2^5}{3^5})\cdot k^{10}$
En dan combineer je alles weer:
$-\frac{2^5 k^{10}}{3^5}$

Bedankt, dit heeft me geholpen!

nog 1 vraagje. waarom kan er eigenlijk nog een 1 komen na de '-' als er al een getal staat? in dit geval een getal kleiner dan 1.

Crack the following and we will get back to you: !1!llssod000;;

dinsdag 7 november 2017 @ 16:48:30 #206

Janneke141

Green, green grass of home

quote:
Op dinsdag 7 november 2017 16:45 schreef _--_ het volgende:

[..]

Bedankt, dit heeft me geholpen!

nog 1 vraagje. waarom kan er eigenlijk nog een 1 komen na de '-' als er al een getal staat? in dit geval een getal kleiner dan 1.

Eeh, omdat je een getal zo vaak als je wil met 1 kan vermenigvuldigen zonder dat er iets verandert?

Opinion is the medium between knowledge and ignorance (Plato)

dinsdag 7 november 2017 @ 16:49:57 #207

_--_

In varietate concordia

quote:
Op dinsdag 7 november 2017 16:48 schreef Janneke141 het volgende:

[..]

Eeh, omdat je een getal zo vaak als je wil met 1 kan vermenigvuldigen zonder dat er iets verandert?

Het is dus altijd zo dat je na een '-' een 1 moet zetten als je een opgave dergelijk moet oplossen?

Crack the following and we will get back to you: !1!llssod000;;

dinsdag 7 november 2017 @ 16:50:42 #208

Janneke141

Green, green grass of home

quote:
Op dinsdag 7 november 2017 16:49 schreef _--_ het volgende:

[..]

Het is dus altijd zo dat je na een '-' een 1 moet zetten als je een opgave dergelijk moet oplossen?

Er moet niks. Je kan ook concluderen dat een oneven macht van een minteken altijd een minteken oplevert, en een even macht niet.

Opinion is the medium between knowledge and ignorance (Plato)

dinsdag 7 november 2017 @ 16:51:17 #209

_--_

In varietate concordia

quote:
Op dinsdag 7 november 2017 16:50 schreef Janneke141 het volgende:

[..]

Er moet niks. Je kan ook concluderen dat een oneven macht van een minteken altijd een minteken oplevert, en een even macht niet.

Bedankt voor de hulp

Crack the following and we will get back to you: !1!llssod000;;

dinsdag 7 november 2017 @ 16:54:16 #210

Alrac4

quote:
Op dinsdag 7 november 2017 16:49 schreef _--_ het volgende:

[..]

Het is dus altijd zo dat je na een '-' een 1 moet zetten als je een opgave dergelijk moet oplossen?

Je kunt het minteken ook bij de 2, de k^2 of zelfs bij de 3 zetten. Als je de 5e macht dan uitwerkt zie je dat je uiteindelijk een minteken overhoudt. Zoals Janneke al zegt kom het er uiteindelijk op neer dat oneven machten van een minteken een minteken opleveren, terwijl even machten een plusteken geven.

dinsdag 7 november 2017 @ 16:56:12 #211

_--_

In varietate concordia

quote:
Op dinsdag 7 november 2017 16:54 schreef Alrac4 het volgende:

[..]

Je kunt het minteken ook bij de 2, de k^2 of zelfs bij de 3 zetten. Als je de 5e macht dan uitwerkt zie je dat je uiteindelijk een minteken overhoudt. Zoals Janneke al zegt kom het er uiteindelijk op neer dat oneven machten van een minteken een minteken opleveren, terwijl even machten een plusteken geven.

Crack the following and we will get back to you: !1!llssod000;;

dinsdag 7 november 2017 @ 17:44:10 #212

Riparius

quote:
Op dinsdag 7 november 2017 15:51 schreef _--_ het volgende:
$\left(-\frac{2}{3}k^2\right)^5=-\frac{2^5k^{10}}{3^5}$
Wat zijn de tussenstappen hier en waarom?

Gewoon gebruik maken van de bekende rekenregels voor breuken en voor machten:

$\left(-\frac{2}{3}k^2\right)^5\,=\,(-1)^5\,\cdot\,(\frac{2}{3})^5\,\cdot\,(k^2)^5\,=\,(-1)\,\cdot\,\frac{2^5}{3^5}\,\cdot\,k^{10}\,=\,-\frac{2^5k^{10}}{3^5}$

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

dinsdag 7 november 2017 @ 20:46:30 #213

_--_

In varietate concordia

quote:
Op dinsdag 7 november 2017 17:44 schreef Riparius het volgende:

[..]

Gewoon gebruik maken van de bekende rekenregels voor breuken en voor machten:

$\left(-\frac{2}{3}k^2\right)^5\,=\,(-1)^5\,\cdot\,(\frac{2}{3})^5\,\cdot\,(k^2)^5\,=\,(-1)\,\cdot\,\frac{2^5}{3^5}\,\cdot\,k^{10}\,=\,-\frac{2^5k^{10}}{3^5}$

Jow bedankt!

Crack the following and we will get back to you: !1!llssod000;;

dinsdag 7 november 2017 @ 20:46:59 #214

_--_

In varietate concordia

-Hehe laat maar.-

Crack the following and we will get back to you: !1!llssod000;;

dinsdag 7 november 2017 @ 21:40:55 #215

Adrie072

quote:
Op dinsdag 7 november 2017 16:40 schreef Alrac4 het volgende:

[..]

Je weet ook dat $(a b)^n = a^nb^n$ .
Dus schrijf $-\frac{2}{3}k^2$ als $(-1)\cdot\frac{2}{3}\cdot k^2$
Dan gebruik je de regel voor vermenigvuldigen:
$(-1)^5\cdot(\frac{2}{3})^5\cdot(k^2)^5$
Dan werk je alle losse termen uit:
$(-1)\cdot(\frac{2^5}{3^5})\cdot k^{10}$
En dan combineer je alles weer:
$-\frac{2^5 k^{10}}{3^5}$

Deze notaties, hoe krijg ik die makkelijk vanaf m`n toetsenbord op het beeld?
Alt + ... invoer, of in een word document eerst intypen/gebruik maken?

woensdag 8 november 2017 @ 00:04:51 #216

#ANONIEM

quote:
Op dinsdag 7 november 2017 21:40 schreef Adrie072 het volgende:

[..]

Deze notaties, hoe krijg ik die makkelijk vanaf m`n toetsenbord op het beeld?
Alt + ... invoer, of in een word document eerst intypen/gebruik maken?

Met LaTex door [tex] tagjes.

woensdag 8 november 2017 @ 18:20:39 #217

Adrie072

quote:
Op woensdag 8 november 2017 00:04 schreef DrNick het volgende:

[..]

Met LaTex door [tex] tagjes.

Bedankt, heb er even vluchtig na gekeken, dat heb je zo te zien niet even onder de knie.

woensdag 8 november 2017 @ 18:57:12 #218

Riparius

quote:
Op woensdag 8 november 2017 18:20 schreef Adrie072 het volgende:

[..]

Bedankt, heb er even vluchtig naar gekeken, dat heb je zo te zien niet even onder de knie.

Het is eenvoudiger dan het lijkt. Werk deze vijf blogs eens door.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

woensdag 8 november 2017 @ 22:03:57 #219

Adrie072

quote:
Op woensdag 8 november 2017 18:57 schreef Riparius het volgende:

[..]

Het is eenvoudiger dan het lijkt. Werk deze vijf blogs eens door.

Ga ik doen, merci

maandag 13 november 2017 @ 14:04:32 #220

obsama

Kan iemand de logica uitleggen van de log2 term in Shannon-entropie? Moest dit gebruiken om de purity van een set uit te rekenen maar kan de log niet plaatsen

https://nl.m.wikipedia.org/wiki/Entropie_(informatietheorie)

Redactie Sport maandag 13 november 2017 @ 14:17:00 #221

Mexicanobakker

quote:
Op woensdag 8 november 2017 18:20 schreef Adrie072 het volgende:

[..]

Bedankt, heb er even vluchtig na gekeken, dat heb je zo te zien niet even onder de knie.

Is wel verdomd handig. Ik wist niet dat FOK! LaTex faciliteerde overigens.

[i]Put me on a pedestal and I'll only disappoint you
Tell me I'm exceptional and I promise to exploit you
Give me all your money and I'll make some origami honey
I think you're a joke but I don't find you very funny[/i]

maandag 13 november 2017 @ 14:17:19 #222

#ANONIEM

quote:
Op maandag 13 november 2017 14:04 schreef obsama het volgende:
Kan iemand de logica uitleggen van de log2 term in Shannon-entropie? Moest dit gebruiken om de purity van een set uit te rekenen maar kan de log niet plaatsen

https://nl.m.wikipedia.org/wiki/Entropie_(informatietheorie)

Omdat ze informatie uitdrukken in aantal bits als ik er zo even kort naar kijk.

Edit:

Ik heb even in de Engelstalige wiki gespiekt en het concept is best interessant.

Het betreft een maat voor de 'voorspelbaarheid' van een (discrete) stochast. Het volgende voorbeeld is denk ik wel duidelijk:

Now consider the example of a coin toss. Assuming the probability of heads is the same as the probability of tails, then the entropy of the coin toss is as high as it could be. This is because there is no way to predict the outcome of the coin toss ahead of time: if we have to choose, the best we can do is predict that the coin will come up heads, and this prediction will be correct with probability 1/2. Such a coin toss has one bit (reken maar eens na) of entropy since there are two possible outcomes that occur with equal probability, and learning the actual outcome contains one bit of information. In contrast, a coin toss using a coin that has two heads and no tails has zero entropy since the coin will always come up heads, and the outcome can be predicted perfectly.

[ Bericht 41% gewijzigd door #ANONIEM op 13-11-2017 20:17:33 ]

zondag 19 november 2017 @ 00:52:35 #223

JAM

Sic transit gloria mundi.

quote:
Op maandag 13 november 2017 14:17 schreef Amoeba het volgende:

[...] (reken maar eens na) [...]

Toch wonderlijk dat ze dat zo op de Engelstalige wiki vermelden.

"The world will note that the first atomic bomb was dropped on Hiroshima, a military base."

zondag 19 november 2017 @ 17:16:52 #224

#ANONIEM

quote:
Op zondag 19 november 2017 00:52 schreef JAM het volgende:

[..]

Toch wonderlijk dat ze dat zo op de Engelstalige wiki vermelden. .

zaterdag 9 december 2017 @ 16:54:25 #225

#ANONIEM

Heb nu een vak Stochastics 2 en kom er echt niet uit. Misschien iemand hier

Een of andere leuke variant op Polya's Urn model:

We hebben een aantal boxen met label {1,..,n}. Zij X_0 het aantal rode ballen in box 0.
In iedere box zitten m ballen. De verdeling van aantal ballen in box i+1 komt zo tot stand: uit box i wordt m keer 1 bal getrokken (met terugleggen) en het resultaat wordt in box i+1 bijgeplaatst.

Dus:

In alle boxen zitten uiteindelijk m ballen. Dit spel gaat door tot Xn = 0 of Xn = m, in dat geval is de staart van de serie triviaal. Dus zij T_0, T_m gedefinieerd als de hitting time van de event X_n = 0 resp X_n = m, dus per definitie: T_0 = inf{ n s.t. X_n = 0}

Gevraagd:

Bereken Pr(T_0 < T_m | X_0 = k)
Het vak gaat nogal over martingale theory dus in die richting word ik ook geacht te zoeken.

Nu is E[ X_{n+1} | X_0, .. , X_n] = m* (X_n/m) = X_n, dus X = (X_n)n>0 zelf een martingale.

Maar hier loop ik een beetje vast. Ik heb het idee dat ik X als een random walk op (-k, m-k) kan zien, maar dat is het dan ook.

[ Bericht 0% gewijzigd door #ANONIEM op 10-12-2017 22:19:44 ]

actieve topics nieuwe topics

abonnement Unibet Coolblue Bitvavo

Forum Opties
Forumhop:
Hop naar:	(afkorting, bv 'KLB')

» school, studie en onderwijs

» school, studie en onderwijs