SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Ik was vanmiddag bezig met mijn wiskunde en liep vast op het volgende
Mijn gr gaf een MA error aan, ik snap niet helemaal wat ik verkeerd heb gedaan, of dat het aan de gr ligt. Het gaat om een casio 9860.
Ziet iemand waar de fout zit? De uitkomst ligt ergens rond de 13 dacht ik.
Mijn gr gaf een MA error aan, ik snap niet helemaal wat ik verkeerd heb gedaan, of dat het aan de gr ligt. Het gaat om een casio 9860.
Ziet iemand waar de fout zit? De uitkomst ligt ergens rond de 13 dacht ik.


Je rekenmachine probeert waarschijnlijk x = 2 in te vullen maar dan deelt hij door 0.quote:Op woensdag 4 maart 2015 23:49 schreef Mopi het volgende:
Ik was vanmiddag bezig met mijn wiskunde en liep vast op het volgende
[ afbeelding ]
Mijn gr gaf een MA error aan, ik snap niet helemaal wat ik verkeerd heb gedaan, of dat het aan de gr ligt. Het gaat om een casio 9860.
Ziet iemand waar de fout zit? De uitkomst ligt ergens rond de 13 dacht ik.
Als je alleen een benadering nodig hebt (wat een antwoord van de rekenmachine natuurlijk altijd al is) kan je als ondergrens 2.001 nemen of zo, en anders gewoon geen rekenmachine gebruiken.


Dat komt al dichter in de buurt, hieruit volgt 15,443, maar het antwoord moet 13,903 zijn. Iemand enig idee? Vind het maar apart, de opgave komt uit een getal en ruimte boek, dus zo lastig zou het niet moeten zijn.quote:Op donderdag 5 maart 2015 00:09 schreef Anoonumos het volgende:
[..]
Je rekenmachine probeert waarschijnlijk x = 2 in te vullen maar dan deelt hij door 0.
Als je alleen een benadering nodig hebt (wat een antwoord van de rekenmachine natuurlijk altijd al is) kan je als ondergrens 2.001 nemen of zo, en anders gewoon geen rekenmachine gebruiken.


quote:Op donderdag 5 maart 2015 00:30 schreef Mopi het volgende:
[..]
Dat komt al dichter in de buurt, hieruit volgt 15,443, maar het antwoord moet 13,903 zijn. Iemand enig idee? Vind het maar apart, de opgave komt uit een getal en ruimte boek, dus zo lastig zou het niet moeten zijn.
De fout is dat je überhaupt een rekenmachine gebruikt in plaats van je grijze massa.quote:Op woensdag 4 maart 2015 23:49 schreef Mopi het volgende:
Ik was vanmiddag bezig met mijn wiskunde en liep vast op het volgende
[ afbeelding ]
Mijn gr gaf een MA error aan, ik snap niet helemaal wat ik verkeerd heb gedaan, of dat het aan de gr ligt. Het gaat om een casio 9860.
Ziet iemand waar de fout zit? De uitkomst ligt ergens rond de 13 dacht ik.
Hint: substitueer
dan is
en krijgen we
Mooi hè?
De exacte waarde van deze integraal is overigens
[ Bericht 6% gewijzigd door Riparius op 05-03-2015 01:22:35 ]


Thanks voor je hulp, ik denk dat mijn wiskunde docent heel erg blij is als ik met dat antwoord op die manier aan kom zetten, maar het gaat er om dat ik het met mijn gr kan en op die 13,903 uit kom. Enig idee?quote:Op donderdag 5 maart 2015 01:11 schreef Riparius het volgende:
[..]
[..]
De fout is dat je überhaupt een rekenmachine gebruikt in plaats van je grijze massa.
Hint: substitueer
dan is
en krijgen we
Mooi hè?
De exacte waarde van deze integraal is overigens


Je GR kan geen oneigenlijke integralen berekenen. Door bovenstaande substitutie zet je de integraal om in een integraal die niet meer oneigenlijk is en die je GR wel kan berekenen. Bereken de integraal met u als variabele maar met je GR, dan zul je zien dat je het (numerieke) antwoord krijgt dat je verwacht.quote:Op donderdag 5 maart 2015 13:28 schreef Mopi het volgende:
[..]
Thanks voor je hulp, ik denk dat mijn wiskunde docent heel erg blij is als ik met dat antwoord op die manier aan kom zetten, maar het gaat er om dat ik het met mijn gr kan en op die 13,903 uit kom. Enig idee?
Als je wil weten hoe ik - uitsluitend met pen en papier - aan het exacte antwoord kom, dan moet je dit maar eens bestuderen.


hoe kom ik op 54,8 uit met de volgende berekening:
(89,3-x)/x = 0,63
(89,3-x)/x = 0,63
I'll watch that pretty life play out in pictures from afar


Wat heb je geprobeerd?quote:Op donderdag 5 maart 2015 15:47 schreef whoyoulove het volgende:
hoe kom ik op 54,8 uit met de volgende berekening:
(89,3-x)/x = 0,63
Wat kan je aan beide kanten van het =-teken doen wat handig kan zijn?
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Oh ik ben zo dom :p Ik heb 'm, dankjewel!quote:Op donderdag 5 maart 2015 15:58 schreef -J-D- het volgende:
[..]
Wat heb je geprobeerd?
Wat kan je aan beide kanten van het =-teken doen wat handig kan zijn?
I'll watch that pretty life play out in pictures from afar


OMG hoe diep zijn we gezonken met het Nederlandse wiskunde onderwijsquote:Op woensdag 4 maart 2015 23:49 schreef Mopi het volgende:
Ik was vanmiddag bezig met mijn wiskunde en liep vast op het volgende
[ afbeelding ]
Mijn gr gaf een MA error aan, ik snap niet helemaal wat ik verkeerd heb gedaan, of dat het aan de gr ligt. Het gaat om een casio 9860.
Ziet iemand waar de fout zit? De uitkomst ligt ergens rond de 13 dacht ik.


Hoe lees ik sin (x) = -(1/2)sqrt2 af op de exacte waardencirkel?
Ik weet dat deze uitkomst op te lossen is door uit de exacte waardencirkel één oplossing B af te lezen, alleen weet ik niet of ik moet kiezen uit 1 (1/4) pi of 1 (3/4) pi. Het antwoordenboek vindt B is -(1/4)pi, alleen geen idee hoe ze daarop komen.
Ik weet dat deze uitkomst op te lossen is door uit de exacte waardencirkel één oplossing B af te lezen, alleen weet ik niet of ik moet kiezen uit 1 (1/4) pi of 1 (3/4) pi. Het antwoordenboek vindt B is -(1/4)pi, alleen geen idee hoe ze daarop komen.


Dat vindt jij het grotere probleem omdat jij graag je GRM wil blijven gebruiken zodat je het niet met de hand hoeft te doen. Een probleem hiermee is dat je het vroeg of laat wel met de hand gaat moeten doen. Op het examen vragen ze tegenwoordig ook regelmatig om integralen met de hand uit te werken en als jij een opleiding gaat volgen waarvoor wiskunde B verplicht is dan moet je zulke integralen 100% zeker met de hand gaan uitwerken, dan mag je geen grafisch rekenmachientje gebruiken. Het is veel verstandiger om daar nu al mee te oefenen. Er is niets mis mee als je dat apparaat gebruikt om te controleren of dat jouw uitwerking klopt, al zijn daar betere middelen voor, maar zorg er voor dat je het zelf kan.quote:Op donderdag 5 maart 2015 13:28 schreef Mopi het volgende:
[..]
Thanks voor je hulp, ik denk dat mijn wiskunde docent heel erg blij is als ik met dat antwoord op die manier aan kom zetten, maar het gaat er om dat ik het met mijn gr kan en op die 13,903 uit kom. Enig idee?
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL


Om te beginnen moet je de sinus en cosinus van een aantal 'standaardhoeken', namelijk 0, 30, 45, 60 en 90 graden, gewoon uit het blote hoofd kennen. Daar is trouwens een eenvoudig ezelsbruggetje voor: de sinus van de genoemde hoeken is namelijk resp.quote:Op zondag 8 maart 2015 20:12 schreef rareziekte het volgende:
Hoe lees ik sin (x) = -(1/2)sqrt2 af op de exacte waardencirkel?
Ik weet dat deze uitkomst op te lossen is door uit de exacte waardencirkel één oplossing B af te lezen, alleen weet ik niet of ik moet kiezen uit 1 (1/4) pi of 1 (3/4) pi. Het antwoordenboek vindt B is -(1/4)pi, alleen geen idee hoe ze daarop komen.
½√0, ½√1, ½√2, ½√3, ½√4
en dus
0, ½, ½√2, ½√3, 1
en de cosinus van de genoemde hoeken krijg je achtereenvolgens door hetzelfde rijtje van rechts naar links op te schrijven.
Met behulp van de definitie van de sinus en de cosinus aan de hand van de eenheidscirkel (zie ook hier) zie je gemakkelijk dat tegengestelde (rotatie)hoeken tegengestelde sinussen hebben, dus
sin(−α) = −sin α
maar dezelfde cosinus, dus
cos(−α) = cos α
Goed, als je nu bedenkt dat sin 45° = ½√2 en dat 45° overeenkomt met ¼π radialen, dus sin(¼π) = ½√2, dan weet je ook dat sin(−¼π) = −½√2.
Nu is het ook nog zo dat supplementaire (rotatie)hoeken dezelfde sinus hebben, dus
sin(π−α) = sin α
maar een tegengestelde cosinus, dus
cos(π−α) = −cos α
Aangezien de sinus van −¼π gelijk is aan −½√2 is de sinus van π − (−¼π) = (5/4)·π dus eveneens gelijk aan −½√2.
Tot slot, de sinus en de cosinus zijn periodieke functies met een periode 2π, dus als complete oplossing van de vergelijking
sin x = −½√2
krijg je zo
x = −¼π + 2kπ ∨ x = (5/4)·π + 2kπ, k ∈ Z
Als je 2π optelt bij −¼π dan krijgen we (7/4)·π, zodat we dus de complete oplossing evengoed als
x = (7/4)·π + 2kπ ∨ x = (5/4)·π + 2kπ, k ∈ Z
kunnen schrijven.
Nu hangt het verder van het vraagstuk af aan welke eventuele andere voorwaarde(n) de gevraagde oplossing(en) moet(en) voldoen, maar aangezien je niet duidelijk maakt wat in je opgave met B wordt bedoeld kan ik hier geen antwoord op geven.
[ Bericht 1% gewijzigd door Riparius op 09-03-2015 02:13:57 ]


Dank je wel, ik snap nu wat mijn boek bedoelt met B, dat is namelijk de eigenlijke oplossing en valt niet af te lezen van de eenheidscirkel, maar met behulp van de eenheidscirkel.quote:Op zondag 8 maart 2015 22:27 schreef Riparius het volgende:
Aangezien de sinus van −¼π gelijk is aan −½√2 is de sinus van π − (−¼π) = (5/4)·π dus eveneens gelijk aan −½√2.
Het boek hanteert namelijk sin (A) = C geeft A=B+k2pi v A=pi-B+k2pi


Kan iemand mij de volgende vraag uitleggen?
- Laat U = W ∩ ℝ[x]5 (waarbij ℝ[x]5 de deelruimte van V is die bestaat uit polynomen van graad kleiner of gelijk aan 5). Bepaal een geordende basis C van U.
W = {f(x) ¤ V | f(0) = f(1) = 0}
Nu weet ik wel hoe je een basis moet bepalen van lineaire deelruimten bestaande uit vergelijkingen en vectoren e.d. Maar heb dit nooit hoeven doen voor polynomen. Iemand die dit kan uitleggen?
- Laat U = W ∩ ℝ[x]5 (waarbij ℝ[x]5 de deelruimte van V is die bestaat uit polynomen van graad kleiner of gelijk aan 5). Bepaal een geordende basis C van U.
W = {f(x) ¤ V | f(0) = f(1) = 0}
Nu weet ik wel hoe je een basis moet bepalen van lineaire deelruimten bestaande uit vergelijkingen en vectoren e.d. Maar heb dit nooit hoeven doen voor polynomen. Iemand die dit kan uitleggen?


hmm dat verduidelijkt het wel iets maar nog niet helemaal. Nog wat tips?quote:Op woensdag 11 maart 2015 21:03 schreef Novermars het volgende:
Kijk hier maar eens: https://math.berkeley.edu/~gmelvin/polyvsrev_m2_54f12.pdf


Ik heb dit zelf nooit gehad op deze manier, maar het is makkelijk om te zien dat elk element van U de volgende vorm heeftquote:Op woensdag 11 maart 2015 21:24 schreef Knuck-les het volgende:
[..]
hmm dat verduidelijkt het wel iets maar nog niet helemaal. Nog wat tips?
De eerste voorwaarde,
De tweede voorwaarde,
De matrix
Hieruit volgt direct dat een basis voor U wordt gegeven door
Zo moet het denk ik, maar ben daar niet zeker van.
[ Bericht 1% gewijzigd door Novermars op 11-03-2015 22:12:07 (Notatie wat verbeterd.) ]


Mathematica geeft trouwens een andere basis van de nulruimte van A aan, namelijk {{-1, 0, 0, 0, 1}, {-1, 0, 0, 1, 0}, {-1, 0, 1, 0, 0}, {-1, 1, 0, 0, 0}}
Ik zou Mathematica vertrouwen, aangezien ik dit uit mijn hoofd heb gedaan. Ik neem aan dat je het antwoord navenant kan aanpassen.
Ik zou Mathematica vertrouwen, aangezien ik dit uit mijn hoofd heb gedaan. Ik neem aan dat je het antwoord navenant kan aanpassen.


Zo is het eindelijk duidelijkquote:Op woensdag 11 maart 2015 21:55 schreef Novermars het volgende:
[..]
Ik heb dit zelf nooit gehad op deze manier, maar het is makkelijk om te zien dat elk element van U de volgende vorm heeft
De eerste voorwaarde,is hier automatisch mee voldaan.
De tweede voorwaarde,impliceert dat
, of in matrix vorm:
De matrixheeft als rank 1, dus volgens de Fundamental Theorem of Linear Algebra volgt dat de nulruimte rank/dimensie 4 heeft. Een basis voor de nulruimte van A is
Hieruit volgt direct dat een basis voor U wordt gegeven door
Zo moet het denk ik, maar ben daar niet zeker van.


Waarom mag je constante polynomen negeren? Punt is dat je argument en conclusie omdraait.quote:Op woensdag 11 maart 2015 21:55 schreef Novermars het volgende:
[..]
Ik heb dit zelf nooit gehad op deze manier, maar het is makkelijk om te zien dat elk element van U de volgende vorm heeft
De eerste voorwaarde,is hier automatisch mee voldaan.
De tweede voorwaarde,impliceert dat
, of in matrix vorm:
De matrixheeft als rank 1, dus volgens de Fundamental Theorem of Linear Algebra volgt dat de nulruimte rank/dimensie 4 heeft. Een basis voor de nulruimte van A is
Hieruit volgt direct dat een basis voor U wordt gegeven door
Zo moet het denk ik, maar ben daar niet zeker van.
[ Bericht 0% gewijzigd door #ANONIEM op 11-03-2015 22:19:58 ]


Je bedoelt dat meteen aanneem dat elementen van U geschreven kunnen worden als f = ax + bx^2 +cx^3 +dx^4 +ex^5? Dat geeft m.i. aan dat ik over het probleem heb nagedacht en niet blind ben begonnen. Het is misschien niet 100% juist geredeneerd, dus ik had er een kanttekening bij mogen zetten, maar weinig mensen die hier over zouden vallen.quote:Op woensdag 11 maart 2015 22:18 schreef Amoeba het volgende:
[..]
Waarom mag je constante polynomen negeren?


En dat doe je omdat f(0)=0? Waardoor de enige 'constante polynoom' f(x)=0 is.quote:Op woensdag 11 maart 2015 22:24 schreef Novermars het volgende:
[..]
Je bedoelt dat meteen aanneem dat elementen van U geschreven kunnen worden als f = ax + bx^2 +cx^3 +dx^4 +ex^5? Dat geeft m.i. aan dat ik over het probleem heb nagedacht en niet blind ben begonnen. Het is misschien niet 100% juist geredeneerd, dus ik had er een kanttekening bij mogen zetten, maar weinig mensen die hier over zouden vallen.


Jouw eerdere vier vectoren zijn lineair onafhankelijk en zitten allemaal in de nulruimte. Omdat de nulruimte ook vierdimensionaal is moeten die vier vectoren wel een basis vormen. Maar een basis is nooit uniek. Bijvoorbeeld {(1,0), (0,1)} en {(2,1),(1,2)} zijn al twee verschillende bases van R^2.quote:Op woensdag 11 maart 2015 22:05 schreef Novermars het volgende:
Mathematica geeft trouwens een andere basis van de nulruimte van A aan, namelijk {{-1, 0, 0, 0, 1}, {-1, 0, 0, 1, 0}, {-1, 0, 1, 0, 0}, {-1, 1, 0, 0, 0}}
Ik zou Mathematica vertrouwen, aangezien ik dit uit mijn hoofd heb gedaan. Ik neem aan dat je het antwoord navenant kan aanpassen.


Wat is precies je vraag/opmerking? In de vraag staat al dat het een subspace/deelruimte(?) is, dus per definitie is de constante polynoom f =0 een element van deze subspace.quote:Op woensdag 11 maart 2015 22:35 schreef thenxero het volgende:
[..]
En dat doe je omdat f(0)=0? Waardoor de enige 'constante polynoom' f(x)=0 is.


Zo'n vermoeden had ik ook al, maar was verbaasd dat Mathematica met deze vier vectoren kwam. Aangezien ik het even snel uit mijn hoofd had gedaan en ik vrij veel vertrouwen heb in Mathematica, heb ik er dit als kanttekening bij gezet.quote:Op woensdag 11 maart 2015 22:38 schreef thenxero het volgende:
[..]
Jouw eerdere vier vectoren zijn lineair onafhankelijk en zitten allemaal in de nulruimte. Omdat de nulruimte ook vierdimensionaal is moeten die vier vectoren wel een basis vormen. Maar een basis is nooit uniek. Bijvoorbeeld {(1,0), (0,1)} en {(2,1),(1,2)} zijn al twee verschillende bases van R^2.


Nou in het algemeen zijn vijfdegraadspolynomen van de vormquote:Op woensdag 11 maart 2015 22:40 schreef Novermars het volgende:
[..]
Wat is precies je vraag/opmerking? In de vraag staat al dat het een subspace/deelruimte(?) is, dus per definitie is de constante polynoom f =0 een element van deze subspace.
f(x) = a + bx + ... + f x^5.
Jij neemt in feite direct a=0 en Amoeba viel daarover. Maar omdat elementen in U voldoen aan f(0)=0, weet je dat f(0)=a=0 en dus kan je die constante weglaten. Ik vroeg me af of dat inderdaad de reden is waarom je de a weglaat in je argument.


Oh, op die fiets. Ja, dat is inderdaad de reden dat ik meteen aannam dat a=0. Misschien had ik inderdaad beter met de volledige vorm kunnen beginnen en met het gegeven f(0)=0 kunnen zeggen dat dat a=0 impliceert.quote:Op woensdag 11 maart 2015 22:45 schreef thenxero het volgende:
[..]
Nou in het algemeen zijn vijfdegraadspolynomen van de vorm
f(x) = a + bx + ... + f x^5.
Jij neemt in feite direct a=0 en Amoeba viel daarover. Maar omdat elementen in U voldoen aan f(0)=0, weet je dat f(0)=a=0 en dus kan je die constante weglaten. Ik vroeg me af of dat inderdaad de reden is waarom je de a weglaat in je argument.


Dat is inderdaad wat ik bedoel met argument en conclusie omdraaien.quote:Op woensdag 11 maart 2015 22:45 schreef thenxero het volgende:
[..]
Nou in het algemeen zijn vijfdegraadspolynomen van de vorm
f(x) = a + bx + ... + f x^5.
Jij neemt in feite direct a=0 en Amoeba viel daarover. Maar omdat elementen in U voldoen aan f(0)=0, weet je dat f(0)=a=0 en dus kan je die constante weglaten. Ik vroeg me af of dat inderdaad de reden is waarom je de a weglaat in je argument.


Om nog maar even een vraag te stellen:
Solve the diffusion equation with variable dissipation:
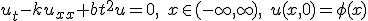
Met b>0.
Solve the diffusion equation with variable dissipation:
Met b>0.


Zie hier.quote:Op woensdag 11 maart 2015 23:45 schreef Novermars het volgende:
Om nog maar even een vraag te stellen:
Solve the diffusion equation with variable dissipation:
Met b>0.


Ik moet het vectorveld 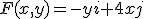 waarbij i en j de cartesische basisvectoren zijn, transformeren naar poolcoördinaten. Ik weet dat
waarbij i en j de cartesische basisvectoren zijn, transformeren naar poolcoördinaten. Ik weet dat 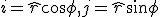 , maar wat moet ik met de (x,y)? Alvast dank!
, maar wat moet ik met de (x,y)? Alvast dank!


Dat klopt alvast niet. Een vector is geen scalar ...quote:Op donderdag 19 maart 2015 15:23 schreef Aardappeltaart het volgende:
Ik moet het vectorveldwaarbij i en j de cartesische basisvectoren zijn, transformeren naar poolcoördinaten. Ik weet dat
,
Het lijkt me de bedoeling dat je F uitdrukt in i en j als functie van de poolcoördinaten (r, φ).quote:maar wat moet ik met de (x,y)? Alvast dank!


Bedankt! Ik vind het best verwarrend dat ze r en r dakje beide gebruiken, komt het daardoor?quote:Op donderdag 19 maart 2015 15:38 schreef Riparius het volgende:
[..]
Dat klopt alvast niet. Een vector is geen scalar ...
[..]
Het lijkt me de bedoeling dat je F uitdrukt in i en j als functie van de poolcoördinaten (r, φ).
Zou iemand me verder kunnen helpen? Ik snap het niet zo goed en mijn boek zegt niks over transformaties.
Behalve:
Meer aanknopingen of een (link naar een) vergelijkbaar voorbeeld zijn erg welkom.


Ah, zo. Verwarrend inderdaad, r is een scalar, r een radiusvector en r̂ een unit radius vector. Zie hier. Je uitdrukking voor φ̂ klopt trouwens niet. Differentiëren vanquote:Op donderdag 19 maart 2015 15:46 schreef Aardappeltaart het volgende:
[..]
Bedankt! Ik vind het best verwarrend dat ze r en r dakje beide gebruiken, komt het daardoor?
Zou iemand me verder kunnen helpen? Ik snap het niet zo goed en mijn boek zegt niks over transformaties.
Behalve: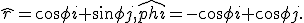
Meer aanknopingen of een (link naar een) vergelijkbaar voorbeeld zijn erg welkom.
naar φ levert een vector op die een kwart slag in tegenwijzerzin is gedraaid en daarmee hebben we
[ Bericht 9% gewijzigd door Riparius op 19-03-2015 16:45:39 ]


Je hebt gelijk, dat was een lelijke overtypfout. Ik heb nu met een trucje de basisvectortransformatie geïnverteerd en x en y naar poolcoördinaten omgeschreven. Het is aan het lukken, hoera!quote:Op donderdag 19 maart 2015 16:30 schreef Riparius het volgende:
[..]
Ah, zo. Verwarrend inderdaad, r is een scalar, r een radiusvector en r̂ een unit radius vector. Zie hier. Je uitdrukking voor φ̂ klopt trouwens niet. Differentiëren van
naar φ levert een vector op die een kwart slag in tegenwijzerzin is gedraaid en daarmee hebben we


Omdat sin^2(x)+cos^2(x) = 1 voor alle x.quote:
Dit kun je inzien door de eenheidscirkel te bekijken:
Voor ieder punt op de eenheidscirkel geldt dat de x-coordinaat wordt gegeven door cos(t), de y-coordinaat wordt gegeven door sin(t). Met de stelling van Pythagoras:
x^2 + y^2 = r^2
met r de straal van de cirkel. Maar je weet dat de straal van de eenheidscirkel 1 is (daarom heet het de eenheidscirkel). Als je in de stelling van Pythagoras dan de x-coordinaat, de y-coordinaat en de straal invult krijg je de formule die je nodig hebt.


Dank jequote:Op dinsdag 24 maart 2015 20:22 schreef Alrac4 het volgende:
[..]
Omdat sin^2(x)+cos^2(x) = 1 voor alle x


Wie kan helpen met de volgende vragen?
A) Bereken de onbepaalde integraal:
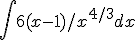
B) Bereken de onbepaalde integraal:
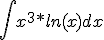
[ Bericht 17% gewijzigd door #ANONIEM op 25-03-2015 12:10:20 ]
A) Bereken de onbepaalde integraal:
B) Bereken de onbepaalde integraal:
[ Bericht 17% gewijzigd door #ANONIEM op 25-03-2015 12:10:20 ]


A) Herschrijf de integrand alsquote:Op woensdag 25 maart 2015 12:04 schreef Thommez het volgende:
Wie kan helpen met de volgende vragen?
A) Bereken de onbepaalde integraal:
B) Bereken de onbepaalde integraal:
B) Gebruik partiële integratie. Zie ook hier.


|| FOK!Stok || tatatatatataatatatattaaaaapiediedieuwtididipieuwpidibididi She said I'll throw myself away pididididum They're just photos after all! || Den Helder || Winnaar VBL Wijndal-award 2020: beste AZ-user! || Mijn concertstatistieken ||


Op een (x,y) vlak, teken de vergelijking 200x+ 300y=q, waarbij je q zelf mag kiezen.quote:
Voor elke q heb je dan een iso-winstlijn.


Dan heb ik nog een vraag, namelijk, stel ik wil sin(t)=(1/2) oplossen, waarom is 1+(2/3)pi +2kpi geen oplossing? (Als je de oplossingen afleest van de eenheidscirkel)quote:Op zondag 8 maart 2015 22:27 schreef Riparius het volgende:
[..]
Om te beginnen moet je de sinus en cosinus van een aantal 'standaardhoeken', namelijk 0, 30, 45, 60 en 90 graden, gewoon uit het blote hoofd kennen. Daar is trouwens een eenvoudig ezelsbruggetje voor: de sinus van de genoemde hoeken is namelijk resp.
½√0, ½√1, ½√2, ½√3, ½√4
en dus
0, ½, ½√2, ½√3, 1
en de cosinus van de genoemde hoeken krijg je achtereenvolgens door hetzelfde rijtje van rechts naar links op te schrijven.
Met behulp van de definitie van de sinus en de cosinus aan de hand van de eenheidscirkel (zie ook hier) zie je gemakkelijk dat tegengestelde (rotatie)hoeken tegengestelde sinussen hebben, dus
sin(−α) = −sin α
maar dezelfde cosinus, dus
cos(−α) = cos α
Goed, als je nu bedenkt dat sin 45° = ½√2 en dat 45° overeenkomt met ¼π radialen, dus sin(¼π) = ½√2, dan weet je ook dat sin(−¼π) = −½√2.
Nu is het ook nog zo dat supplementaire (rotatie)hoeken dezelfde sinus hebben, dus
sin(π−α) = sin α
maar een tegengestelde cosinus, dus
cos(π−α) = −cos α
Aangezien de sinus van −¼π gelijk is aan −½√2 is de sinus van π − (−¼π) = (5/4)·π dus eveneens gelijk aan −½√2.
Tot slot, de sinus en de cosinus zijn periodieke functies met een periode 2π, dus als complete oplossing van de vergelijking
sin x = −½√2
krijg je zo
x = −¼π + 2kπ ∨ x = (5/4)·π + 2kπ, k ∈ Z
Als je 2π optelt bij −¼π dan krijgen we (7/4)·π, zodat we dus de complete oplossing evengoed als
x = (7/4)·π + 2kπ ∨ x = (5/4)·π + 2kπ, k ∈ Z
kunnen schrijven.
Nu hangt het verder van het vraagstuk af aan welke eventuele andere voorwaarde(n) de gevraagde oplossing(en) moet(en) voldoen, maar aangezien je niet duidelijk maakt wat in je opgave met B wordt bedoeld kan ik hier geen antwoord op geven.


De oplossingen moeten in ieder geval rationale veelvouden zijn van π omdat sin(⅙π) = ½, dus de waarde die jij geeft is zeker geen oplossing. Of misschien bedoel je (5/3)·π + 2kπ, k ∈ Z, maar ook dat is geen oplossing van je vergelijking. Immers, je hebt π < (5/3)·π < 2π, dus als je het startpunt (1; 0) om de oorsprong roteert over een hoek van (5/3)·π radialen dan kom je uit op een punt onder de x-as, en daar is de y-coördinaat, en dus ook de sinus, negatief, zodat het evident is dat de sinus van (5/3)·π + 2kπ, k ∈ Z negatief moet zijn en niet ½ kan zijn.quote:Op donderdag 2 april 2015 13:44 schreef rareziekte het volgende:
[..]
Dan heb ik nog een vraag, namelijk, stel ik wil sin(t)=(1/2) oplossen, waarom is 1+(2/3)pi +2kpi geen oplossing? (Als je de oplossingen afleest van de eenheidscirkel)
Kijk nog eens naar het volgende plaatje:
We weten dat sin 30° = ½ en dat 30° gelijk is aan 1/6 deel van een gestrekte hoek en daarmee overeenkomt met π/6 rad zodat sin(⅙π) = ½. En omdat supplementaire hoeken dezelfde sinus hebben is dus ook sin 150° = ½ oftewel sin(⅚π) = ½.
Dit kun je ook in het plaatje aflezen, want driehoek OPQ in het tweede kwadrant is congruent met de gestreept getekende driehoek in het eerste kwadrant. Bedenk hierbij dat de sinus van een gegeven (rotatie)hoek per definitie de y-coördinaat is van het beeld van het startpunt (1; 0) bij een rotatie om de oorsprong over de gegeven hoek.
Verder komen we altijd weer op dezelfde punten op de eenheidscirkel uit na een extra rotatie om de oorsprong over een willekeurig aantal gehele slagen in tegenwijzerzin (positief) of in wijzerzin (negatief). Een volledige rotatie om de oorsprong komt overeen met een rotatie over 360° oftewel 2π radialen, en als complete oplossing van de vergelijking sin(t) = ½ krijgen we dus:
t = ⅙π + 2kπ ∨ t = ⅚π + 2kπ, k ∈ Z
[ Bericht 0% gewijzigd door Riparius op 02-04-2015 20:58:40 ]


Ik ben bezig met het vereenvoudigen van een som, alleen snap ik 1 stap niet. Kan iemand me hieruit helpen?
-2500e^-0,5t x 2(1+20e^-0,5t) x 20e^-0,5t x -0,5
Wordt
50000e^-0,5t x e^-0,5t x (1+20e^-0,5t)
Ik snap niet hoe ze bij dat laatste deel aan die e^-0,5t komen
-2500e^-0,5t x 2(1+20e^-0,5t) x 20e^-0,5t x -0,5
Wordt
50000e^-0,5t x e^-0,5t x (1+20e^-0,5t)
Ik snap niet hoe ze bij dat laatste deel aan die e^-0,5t komen



 Op
Op 