SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d


Hoi, kan iemand dit verklaren? Ik snap namelijk niet waarom het dezelfde determinant zal hebben als de determinant van een eenheidsmatrix? Waarvoor dient overigens die 2 die staat bij | i2 | ?


Hint: det(A)det(B) = det(AB) (Met A en B natuurlijk vierkante matrices)quote:Op maandag 16 februari 2015 20:51 schreef RustCohle het volgende:
Hoi, kan iemand dit verklaren? Ik snap namelijk niet waarom het dezelfde determinant zal hebben als de determinant van een eenheidsmatrix? Waarvoor dient overigens die 2 die staat bij | i2 | ?
[ afbeelding ]
Die twee staat voor de dimensie van de betreffende eenheidsmatrix. In dit geval dus 2x2.


Echt waar?!quote:Op maandag 16 februari 2015 21:06 schreef jatochneetoch het volgende:
Een matrix keer zijn(/haar?) inverse is toch altijd de eenheidsmatrix?


Ik snap niet dat als je A vermenigvuldigt met de inverse van A dat je dan een eenheidsmatrix krijgt..quote:Op maandag 16 februari 2015 21:45 schreef jatochneetoch het volgende:
[..]
Als het het zelfde is, dan is het toch ook logisch dat de determinant het zelfde is


Hoezo zeg je dan 'echt waar?!'?quote:Op maandag 16 februari 2015 22:16 schreef RustCohle het volgende:
[..]
Ik snap niet dat als je A vermenigvuldigt met de inverse van A dat je dan een eenheidsmatrix krijgt..
Volgensmij is dat de definitie.


De reden dat ik dat zeg, is omdat ik dat niet wist/weet.quote:Op maandag 16 februari 2015 22:28 schreef jatochneetoch het volgende:
[..]
Hoezo zeg je dan 'echt waar?!'?
Volgensmij is dat de definitie.


Waarom lees je dan niet eerst je slides doorquote:Op maandag 16 februari 2015 22:32 schreef RustCohle het volgende:
[..]
De reden dat ik dat zeg, is omdat ik dat niet wist/weet.
Onoverwinnelijk/Rotterdam/Zeerover
https://www.playgwent.com/en/ - Official beta of Gwent: The Witcher Gard Game
https://www.playgwent.com/en/ - Official beta of Gwent: The Witcher Gard Game


Lees je uberhaupt wat voordat je vragen stelt?quote:
[ Bericht 6% gewijzigd door t4rt4rus op 17-02-2015 00:21:04 (In de war met vector norm, heerlijk die streepjes) ]


Hoe hebben ze je dan uitgelegd wat een inverse matrix is?quote:Op maandag 16 februari 2015 22:32 schreef RustCohle het volgende:
[..]
De reden dat ik dat zeg, is omdat ik dat niet wist/weet.
Opinion is the medium between knowledge and ignorance (Plato)


Alleen de mogelijkheden uitgelegd waarmee je een inverse kan berekenen. Dit soort eigenschappen kwamen niet aan de orde..quote:Op dinsdag 17 februari 2015 00:13 schreef Janneke141 het volgende:
[..]
Hoe hebben ze je dan uitgelegd wat een inverse matrix is?


Een hele goedenavond!
Ik heb een vraagje met betrekking tot lineair programmeren; als ik zowel de doelfunctie als de voorwaardelijke functies opschrijf als x2 = .... ,dan vraag ik mij af hoe ik deze vraag kan oplossen, want waar moet ik een begrenzing trekken, aangezien ik bijvoorbeeld bij die eerste voorwaardelijke functie krijg: x2 < 5 - x1?
Ik heb een vraagje met betrekking tot lineair programmeren; als ik zowel de doelfunctie als de voorwaardelijke functies opschrijf als x2 = .... ,dan vraag ik mij af hoe ik deze vraag kan oplossen, want waar moet ik een begrenzing trekken, aangezien ik bijvoorbeeld bij die eerste voorwaardelijke functie krijg: x2 < 5 - x1?


Heb je een tekening gemaakt van het toegestane gebied?quote:Op dinsdag 17 februari 2015 19:05 schreef Super-B het volgende:
Een hele goedenavond!
Ik heb een vraagje met betrekking tot lineair programmeren; als ik zowel de doelfunctie als de voorwaardelijke functies opschrijf als x2 = .... ,dan vraag ik mij af hoe ik deze vraag kan oplossen, want waar moet ik een begrenzing trekken, aangezien ik bijvoorbeeld bij die eerste voorwaardelijke functie krijg: x2 < 5 - x1?
[ afbeelding ]
Opinion is the medium between knowledge and ignorance (Plato)


Wiskunde 2 tentamen komt er weer aan?
Onoverwinnelijk/Rotterdam/Zeerover
https://www.playgwent.com/en/ - Official beta of Gwent: The Witcher Gard Game
https://www.playgwent.com/en/ - Official beta of Gwent: The Witcher Gard Game


Het hele trimester hebben ze geen vragen, en nu komen ze hoor.quote:Op dinsdag 17 februari 2015 19:31 schreef CapnIzzy het volgende:
Wiskunde 2 tentamen komt er weer aan?


Ik heb de lijnen getekend. Ik weet alleen niet op welke coördinaten de begrenzingen liggen per voorwaardefunctie, aangezien ik de functies heb omgeschreven naar de vorm x2 =...quote:Op dinsdag 17 februari 2015 19:18 schreef Janneke141 het volgende:
[..]
Heb je een tekening gemaakt van het toegestane gebied?


Ik ben oprecht benieuwd wat je dan getekend hebt. Bij mij ziet het er in ieder geval zo uit:quote:Op dinsdag 17 februari 2015 20:45 schreef Super-B het volgende:
[..]
Ik heb de lijnen getekend. Ik weet alleen niet op welke coördinaten de begrenzingen liggen per voorwaardefunctie, aangezien ik de functies heb omgeschreven naar de vorm x2 =...
Het gele gebied valt binnen de grenzen. Je doelfunctie is van de vorm x2 = -x1/4 + C, en het is niet moeilijk te zien op welk hoekje van het gele gebied die komt te liggen voor C maximaal.
Opinion is the medium between knowledge and ignorance (Plato)


Goedemiddag,
Ik heb een aantal puzzels gemaakt uit het boek 'The Heart of Mathematics' (http://www.amazon.com/Hea(...)hematics+4th+edition) en daar flink van genoten. Nu wil ik eigenlijk het hele boek aanschaffen maar die is me wat duur. De vraag is dan ook, zijn jullie bekend met soortgelijke boeken? en wat zijn de aanraders?
Ik heb zelf deze gevonden (http://www.bol.com/nl/p/c(...)zz/1001004002432820/) en die spreekt me best aan, maar ik hoor graag nog wat andere tips. 'Oudere' gratis E-boeken zijn natuurlijk ook welkom, maar vind het wel erg prettig om met een boek aan tafel te kunnen gaan zitten ipv de laptop of tablet.
Alvast bedankt! (verwante boeken zijn ook welkom)
Ik heb een aantal puzzels gemaakt uit het boek 'The Heart of Mathematics' (http://www.amazon.com/Hea(...)hematics+4th+edition) en daar flink van genoten. Nu wil ik eigenlijk het hele boek aanschaffen maar die is me wat duur. De vraag is dan ook, zijn jullie bekend met soortgelijke boeken? en wat zijn de aanraders?
Ik heb zelf deze gevonden (http://www.bol.com/nl/p/c(...)zz/1001004002432820/) en die spreekt me best aan, maar ik hoor graag nog wat andere tips. 'Oudere' gratis E-boeken zijn natuurlijk ook welkom, maar vind het wel erg prettig om met een boek aan tafel te kunnen gaan zitten ipv de laptop of tablet.
Alvast bedankt! (verwante boeken zijn ook welkom)


Ik zou als eerste denken het meest rechtse punt (waar y=0 en x=5), omdat je de lijn verder naar rechts kan verschuiven dan het snijpunt van de twee lijnen: 2+x1 en 5 - x1.quote:Op dinsdag 17 februari 2015 20:59 schreef Janneke141 het volgende:
[..]
Ik ben oprecht benieuwd wat je dan getekend hebt. Bij mij ziet het er in ieder geval zo uit:
[ afbeelding ]
Het gele gebied valt binnen de grenzen. Je doelfunctie is van de vorm x2 = -x1/4 + C, en het is niet moeilijk te zien op welk hoekje van het gele gebied die komt te liggen voor C maximaal.


Hallo,
Kan iemand mij vertellen hoe ik hier een differentievergelijking van moet maken? Ik ben namelijk niet zo goed in het omzetten van verhaaltjes.. :
Ik had zelf bij a) :
Y(t+1) = 900Yt + 100t
Kan iemand mij vertellen hoe ik hier een differentievergelijking van moet maken? Ik ben namelijk niet zo goed in het omzetten van verhaaltjes.. :
Ik had zelf bij a) :
Y(t+1) = 900Yt + 100t


Dat is helemaal fout.quote:Op donderdag 19 februari 2015 12:25 schreef RustCohle het volgende:
Hallo,
Kan iemand mij vertellen hoe ik hier een differentievergelijking van moet maken? Ik ben namelijk niet zo goed in het omzetten van verhaaltjes.. :
[ afbeelding ]
[ afbeelding ]
Ik had zelf bij a) :
Y(t+1) = 900Yt + 100t
Je begint met 900 bacteriën, daar moet je niet mee vermenigvuldigen.
En er komen er elke dag 100 bij niet 100t.


Die t staat voor het aantal dagen, dus bij 3 dagen, heb je 300 bacteriën erbij dacht ik? Die 900 moet dan de beginwaarde zijn: Y0 ?quote:Op donderdag 19 februari 2015 12:38 schreef t4rt4rus het volgende:
[..]
Dat is helemaal fout.
Je begint met 900 bacteriën, daar moet je niet mee vermenigvuldigen.
En er komen er elke dag 100 bij niet 100t.


Ja je beginwaarde isquote:Op donderdag 19 februari 2015 12:42 schreef RustCohle het volgende:
[..]
Die t staat voor het aantal dagen, dus bij 3 dagen, heb je 300 bacteriën erbij dacht ik? Die 900 moet dan de beginwaarde zijn: Y0 ?
Het is geen directe formule, je moet een differentievergelijking opstellen.
Wat je ook aan het doen was...
Waar gebruik je die t en t+1 anders voor?
Trouwens, heb je je boek al gelezen?
Daar staat vast in wat een differentievergelijking is.


Ja daar staat in dat een differentievergelijking een vergelijking is met een differentie erin (ofwel een verschil). Die y0 is je beginwaarde en naarmate de tijd vordert (t) wordt, kun je door middel van y0 en de rest van de vergelijking yt berekenen (Y op elk moment van t).quote:Op donderdag 19 februari 2015 12:44 schreef t4rt4rus het volgende:
[..]
Ja je beginwaarde is
Het is geen directe formule, je moet een differentievergelijking opstellen.
Wat je ook aan het doen was...
Waar gebruik je die t en t+1 anders voor?
Trouwens, heb je je boek al gelezen?
Daar staat vast in wat een differentievergelijking is.


Nou doe dat danquote:Op donderdag 19 februari 2015 12:49 schreef RustCohle het volgende:
[..]
Ja daar staat in dat een differentievergelijking een vergelijking is met een differentie erin (ofwel een verschil). Die y0 is je beginwaarde en naarmate de tijd vordert (t) wordt, kun je door middel van y0 en de rest van de vergelijking yt berekenen (Y op elk moment van t).


Beargumenteer dat eens.quote:
Dan kom je eruit dat het nergens op slaat.
Zie ook mijn eerste en tweede reactie.
Oké een hint.
Nu hoeft jij alleen nog a en b te geven en een beginwaarde die we ook al eerder hebben besproken, maar die je al weer bent vergeten.


Y{t+1} = 2Yt + 100t, waarbij Y0 = 900.quote:Op donderdag 19 februari 2015 13:39 schreef t4rt4rus het volgende:
[..]
Beargumenteer dat eens.
Dan kom je eruit dat het nergens op slaat.
Zie ook mijn eerste en tweede reactie.
Oké een hint.
Nu hoeft jij alleen nog a en b te geven en een beginwaarde die we ook al eerder hebben besproken, maar die je al weer bent vergeten.
Ik betwijfel of het 100 of 100t is, aangezien er staat dat er elke dag 100 bijkomen.., lijkt het mij logisch om 100t te zetten, want na 2 dagen zijn er dan +200 bijgekomen.


Nee, je redeneert niet logisch (of je redeneert helemaal niet en doet maar wat). Het verschil tussen yt+1 en yt is gelijk aan yt vermeerderd met 100.quote:Op donderdag 19 februari 2015 15:41 schreef RustCohle het volgende:
[..]
Yt+1 = 2Yt + 100t, waarbij Y0 = 900.
Ik twijfel of het 100 of 100t is, aangezien er staat dat er elke dag 100 bijkomen.., lijkt het mij logisch om 100t te zetten, want na 2 dagen zijn er dan +200 bijgekomen.


Hallo mensen,
Ik heb zelf wiskunde A en doe m'n PWS over natuurkunde. Ik onderzoek hoe diep we door de aarde een soort metro kunnen bouwen. Ik heb berekend dat dat ongeveer 19 km is. Ik moet nu de hoek van de tunnel met de aarde, de afstand door de aarde (een rechte lijn met diepste punt dus 19 km, zoals dit) en de afstand die we anders over het land afgelegd zouden hebben berekenen. Hier kom ik denk ik met mijn Wiskunde A tekort. Ik snap dat dit misschien moeilijk te begrijpen is.
Ik begon met de stelling van pythagoras. Zo kon ik met een driehoek tussen het middelpunt van de aarde, het diepste punt van de lijn/tunnel en het begin van de lijn/tunnel. Zo kwam ik op een totale afstand door de aarde van 984 km.
Daarna wilde ik de afstand die we anders over de aarde af zouden leggen berekenen. maar daar kwam ik op 17 km uit.
Iemand enig idee hoe ik dat zou moeten berekenen?
Ik heb zelf wiskunde A en doe m'n PWS over natuurkunde. Ik onderzoek hoe diep we door de aarde een soort metro kunnen bouwen. Ik heb berekend dat dat ongeveer 19 km is. Ik moet nu de hoek van de tunnel met de aarde, de afstand door de aarde (een rechte lijn met diepste punt dus 19 km, zoals dit) en de afstand die we anders over het land afgelegd zouden hebben berekenen. Hier kom ik denk ik met mijn Wiskunde A tekort. Ik snap dat dit misschien moeilijk te begrijpen is.
Ik begon met de stelling van pythagoras. Zo kon ik met een driehoek tussen het middelpunt van de aarde, het diepste punt van de lijn/tunnel en het begin van de lijn/tunnel. Zo kwam ik op een totale afstand door de aarde van 984 km.
Daarna wilde ik de afstand die we anders over de aarde af zouden leggen berekenen. maar daar kwam ik op 17 km uit.
Iemand enig idee hoe ik dat zou moeten berekenen?
leef de leven


Nog even terug naar mijn eerste vraag.quote:Op donderdag 19 februari 2015 15:41 schreef RustCohle het volgende:
[..]
Y{t+1} = 2Yt + 100t, waarbij Y0 = 900.
Ik betwijfel of het 100 of 100t is, aangezien er staat dat er elke dag 100 bijkomen.., lijkt het mij logisch om 100t te zetten, want na 2 dagen zijn er dan +200 bijgekomen.
Heb je het boek al gelezen?
Want je doet nu maar wat.


Je bent er bijna.quote:Op donderdag 19 februari 2015 17:24 schreef RRuben het volgende:
Iemand enig idee hoe ik dat zou moeten berekenen?
In dezelfde driehoek die je al getekend hebt kan je de hoek berekenen tussen de twee lijnen loodrecht met het oppervlak.
Dit kan je doen met de trigonometrische functies, de cosinus in dit geval.
Heb je die hoek dan kan je ook de lengte van de kromme berekenen.
[ Bericht 0% gewijzigd door t4rt4rus op 19-02-2015 20:18:53 ]


Noem de straal van de aarde R en de grootste diepte van je tunnel d, dan geldt voor de lengte L van de tunnelquote:Op donderdag 19 februari 2015 17:24 schreef RRuben het volgende:
Hallo mensen,
Ik heb zelf wiskunde A en doe m'n PWS over natuurkunde. Ik onderzoek hoe diep we door de aarde een soort metro kunnen bouwen. Ik heb berekend dat dat ongeveer 19 km is. Ik moet nu de hoek van de tunnel met de aarde, de afstand door de aarde (een rechte lijn met diepste punt dus 19 km, zoals dit) en de afstand die we anders over het land afgelegd zouden hebben berekenen. Hier kom ik denk ik met mijn Wiskunde A tekort. Ik snap dat dit misschien moeilijk te begrijpen is.
Ik begon met de stelling van Pythagoras. Zo kon ik met een driehoek tussen het middelpunt van de aarde, het diepste punt van de lijn/tunnel en het begin van de lijn/tunnel een berekening maken. Zo kwam ik op een totale afstand door de aarde van 984 km.
Daarna wilde ik de afstand die we anders over de aarde af zouden leggen berekenen. maar daar kwam ik op 17 km uit.
Iemand enig idee hoe ik dat zou moeten berekenen?
Met R ≈ 6371 km en d = 19 km komen we dan inderdaad op L ≈ 983,3 km.
Noem nu de hoek tussen de straal vanuit het middelpunt van de aarde naar het begin van de tunnel en het lijnstuk vanuit het middelpunt van de aarde naar het midden van de tunnel α, dan hebben we verder
en daarmee
Dit is tevens de hoek die de tunnel aan de beide uiteinden met het aardoppervlak maakt (maak een tekening om te begrijpen waarom dit zo is).
De (kortste) afstand A over het aardoppervlak tussen het beginpunt en het eindpunt van de tunnel is nu een cirkelboog die een middelpuntshoek 2α omspant. Drukken we α uit in radialen, dan is A gelijk aan 2α/2π maal de omtrek 2πR van de aarde en krijgen we dus
Nu mag je zelf α en A nog even uitrekenen.
[ Bericht 0% gewijzigd door Riparius op 19-02-2015 22:02:52 ]


Ik heb het syllabus gelezen ja. Ik ben er al uit:quote:Op donderdag 19 februari 2015 18:06 schreef t4rt4rus het volgende:
[..]
Nog even terug naar mijn eerste vraag.
Heb je het boek al gelezen?
Want je doet nu maar wat.
Yt = 2y0 + 100


Nee, maar leg eens uit wat je doet.quote:Op donderdag 19 februari 2015 20:20 schreef RustCohle het volgende:
[..]
Ik heb het syllabus gelezen ja. Ik ben er al uit:
Yt = 2y0 + 100
Gewoon even in woorden uitleggen wat er staat.


Oke bedankt voor de antwoorden! Kijk er morgen nog even goed naar, maar ik hiermee lukt het denk ik wel 
leef de leven


Nee. Je hebt je syllabus dan misschien gelezen, maar zeker niet begrepen. Bovenstaande betrekking impliceert dat het aantal bacteriën yt op tijdstip t constant zou zijn, maar het is gegeven dat dat niet zo is. Je begrijpt er dus nog steeds niets van, en ik heb dan ook ernstige twijfels of je iets begrepen hebt van mijn eerdere antwoord op je vraag over een lineaire eerste orde inhomogene differentievergelijking (c.q. recurrente betrekking) met constante coëfficiënten.quote:Op donderdag 19 februari 2015 20:20 schreef RustCohle het volgende:
[..]
Ik heb het de syllabus gelezen ja. Ik ben er al uit:
yt = 2y0 + 100
Gegeven is dat het aantal bacteriën zich elke dag verdubbelt en dat daar, eveneens elke dag, nog eens 100 bacteriën van buitenaf bij komen. Anders gezegd, de toename van het aantal bacteriën tussen tijdstip t en tijdstip t+1 (uitgedrukt in dagen) is gelijk aan het aantal bacteriën op tijdstip t vermeerderd met 100. Deze toename is niets anders dan het verschil tussen yt+1 en yt zodat we dus hebben
oftewel
oftewel
Dit is de gevraagde (inhomogene) differentievergelijking. Los deze nu op volgens de methode die ik eerder heb aangegeven, namelijk door eerst de algemene oplossing te bepalen van de corresponderende homogene differentievergelijking
en door een particuliere oplossing te bepalen van de inhomogene differentievergelijking. De algemene oplossing van de inhomogene differentievergelijking met constante coëfficiënten is dan de som van de algemene oplossing van de homogene differentievergelijking en een particuliere oplossing van de inhomogene differentievergelijking, zie ook hier.
Heb je de algemene oplossing van de inhomogene differentievergelijking bepaald, dan kun je vervolgens de unieke oplossing bepalen die voldoet aan de beginvoorwaarde
[ Bericht 3% gewijzigd door Riparius op 20-02-2015 03:13:59 ]


Ja. Doordat je zo'n beroerde schets hebt gemaakt, kun je niet zien dat de lijn x1+x2=3, oftewel je eerste voorwaarde, dwars door het rode gebied gaat.quote:Op vrijdag 20 februari 2015 21:33 schreef Super-B het volgende:
Snapt iemand wat ik fout doe?:
[ afbeelding ]
[ afbeelding ]
Opinion is the medium between knowledge and ignorance (Plato)


Hello everyone,
Ligt het aan mij of moet het eindantwoord niet 1 - e-11 zijn? Dus dat het -11 is in plaats van 11 in de macht van e?
Ligt het aan mij of moet het eindantwoord niet 1 - e-11 zijn? Dus dat het -11 is in plaats van 11 in de macht van e?


Krijgen we daar nog een opgave bij, of moeten we die zelf verzinnen?quote:Op vrijdag 20 februari 2015 22:03 schreef Andijvie_ het volgende:
Hello everyone,
Ligt het aan mij of moet het eindantwoord niet 1 - e-11 zijn? Dus dat het -11 is in plaats van 11 in de macht van e?
Zo niet, dan moet het eindantwoord 42 zijn.
[ Bericht 7% gewijzigd door Janneke141 op 20-02-2015 22:13:59 ]
Opinion is the medium between knowledge and ignorance (Plato)


Plakken ging niet goed:quote:Op vrijdag 20 februari 2015 22:07 schreef Janneke141 het volgende:
[..]
Krijgen we daar nog een opgave bij, of moeten we die zelf verzinnen?
Zo niet, dan moet het eindantwoord 42 zijn.


Moet inderdaad -11 zijn.quote:Op vrijdag 20 februari 2015 22:30 schreef Andijvie_ het volgende:
[..]
Plakken ging niet goed:
[ afbeelding ]
Opinion is the medium between knowledge and ignorance (Plato)


Klopt. Het moet inderdaad een plus zijn.quote:Op vrijdag 20 februari 2015 23:04 schreef Andijvie_ het volgende:
[..]
Nog één:
[ afbeelding ]
Moet het niet X2 = 2 + 2X3 zijn in plaats van X2 = 2 - 2X3 ?


Dat wordt feest volgende weekquote:Op vrijdag 20 februari 2015 21:33 schreef Super-B het volgende:
Snapt iemand wat ik fout doe?:
[ afbeelding ]
[ afbeelding ]
Onoverwinnelijk/Rotterdam/Zeerover
https://www.playgwent.com/en/ - Official beta of Gwent: The Witcher Gard Game
https://www.playgwent.com/en/ - Official beta of Gwent: The Witcher Gard Game


Kan iemand me helpen met het volgende probleem: Geef de differentiaal en afgeleide van sp(AX^-1) met X een inverteerbare matrix en A een constante matrix.
Edit: laat maar, heb hem al gevonden via de standaardafgeleide van X^-1
[ Bericht 21% gewijzigd door Wouterw17 op 21-02-2015 12:11:14 ]
Edit: laat maar, heb hem al gevonden via de standaardafgeleide van X^-1
[ Bericht 21% gewijzigd door Wouterw17 op 21-02-2015 12:11:14 ]


Toppie, heb er nog één:quote:Op vrijdag 20 februari 2015 23:13 schreef Ensemble het volgende:
[..]
Klopt. Het moet inderdaad een plus zijn.
Moet het niet -2x ln (x) zijn in plaats van -x ln (x)?


Nee, je hebt een factor 1/2 in je 1/(2sqrt(x)) en je krijgt een 1/2 van ln(sqrt(x)) = 1/2 * ln(x)quote:Op zaterdag 21 februari 2015 13:32 schreef Andijvie_ het volgende:
[..]
Toppie, heb er nog één:
[ afbeelding ]
Moet het niet -2x ln (x) zijn in plaats van -x ln (x)?


ohhhh dankje..quote:Op zaterdag 21 februari 2015 13:36 schreef Alrac4 het volgende:
[..]
Nee, je hebt een factor 1/2 in je 1/(2sqrt(x)) en je krijgt een 1/2 van ln(sqrt(x)) = 1/2 * ln(x)


Nee. -x ln(x) is gewoon goed. Hint: ln(sqrt(x)) = 1/2ln(x).quote:Op zaterdag 21 februari 2015 13:32 schreef Andijvie_ het volgende:
[..]
Toppie, heb er nog één:
[ afbeelding ]
Moet het niet -2x ln (x) zijn in plaats van -x ln (x)?
Edit: Ah te laat. Zag de nieuwe pagina nog niet.


Ik moet voor een verslag weten voor welke positieve Kd (afhankelijk van alle andere positieve parameters) geldt:
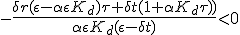
Ik wil graag weten hoe ik dit ofwel op een handige manier kan bepalen, ofwel door middel van Mathematica kan bepalen. Kan iemand me helpen? Dank!
Ik wil graag weten hoe ik dit ofwel op een handige manier kan bepalen, ofwel door middel van Mathematica kan bepalen. Kan iemand me helpen? Dank!


Je hebt een minteken vóór je quotiënt staan, dus het quotiënt zelf moet positief zijn. Dit is het geval als hetzij teller en noemer beide positief zijn hetzij teller en noemer beide negatief zijn. Aldus krijg je twee sets van twee lineaire ongelijkheden in Kd waarbij gelijktijdig aan beide ongelijkheden binnen een set moet worden voldaan en waaruit je kunt herleiden aan welke voorwaarde(n) Kd moet voldoen.quote:Op zaterdag 21 februari 2015 14:55 schreef Aardappeltaart het volgende:
Ik moet voor een verslag weten voor welke positieve Kd (afhankelijk van alle andere positieve parameters) geldt:
Ik wil graag weten hoe ik dit ofwel op een handige manier kan bepalen, ofwel door middel van Mathematica kan bepalen. Kan iemand me helpen? Dank!


Bedankt. Ik hoopte dat het makkelijker kon dan met gevalonderscheiding.quote:Op zaterdag 21 februari 2015 15:07 schreef Riparius het volgende:
[..]
Je hebt een minteken vóór je quotiënt staan, dus het quotiënt zelf moet positief zijn. Dit is het geval als hetzij teller en noemer beide positief zijn hetzij teller en noemer beide negatief zijn. Aldus krijg je twee sets van twee lineaire ongelijkheden in Kd waarbij gelijktijdig aan beide ongelijkheden binnen een set moet worden voldaan en waaruit je kunt herleiden aan welke voorwaarde(n) Kd moet voldoen.
Weet iemand toevallig hoe ik deze antwoorden vind met Mathematica? Met Solve[] lukt het me niet...


Ben er door het hier posten achtergekomen dat ik ergens in een tussenstap een T geïntroduceerd heb die de Tau op een paar plaatsen vervangen heeft. Dit maakt dingen makkelijker...


Dit zal geen unieke oplossing hebben.quote:Op maandag 23 februari 2015 17:51 schreef Borizzz het volgende:
Ik kwam deze tegen
Wie lost 'm op?
[ afbeelding ]
Opinion is the medium between knowledge and ignorance (Plato)


Dat vroeg ik ook niet.quote:Op maandag 23 februari 2015 17:57 schreef Janneke141 het volgende:
[..]
Dit zal geen unieke oplossing hebben.
kloep kloep


Zit hier een grap achter ofzo?quote:Op maandag 23 februari 2015 17:51 schreef Borizzz het volgende:
Ik kwam deze tegen
Wie lost 'm op?
[ afbeelding ]
x=7, y=0, z=0 geeft 7*wortel(2). En nu?


plus 17.quote:Op maandag 23 februari 2015 19:07 schreef thenxero het volgende:
[..]
Zit hier een grap achter ofzo?
x=7, y=0, z=0 geeft 7*wortel(2). En nu?
En x=0, y=0, z=7 geeft iets heel anders. Als dit een of ander raadsel is, ontgaat ie mij ook.
Opinion is the medium between knowledge and ignorance (Plato)


Ik kwam hem tegen op FB; een post van de docentenopleiding aan de FLOT.quote:Op maandag 23 februari 2015 19:12 schreef Janneke141 het volgende:
[..]
plus 17.
En x=0, y=0, z=7 geeft iets heel anders. Als dit een of ander raadsel is, ontgaat ie mij ook.
kloep kloep


Het is volslagen onduidelijk wat de opgave is. Wellicht is het de bedoeling om gehele waarden te vinden voor x, y en z zodanig dat de uitdrukking op de tweede regel eveneens geheel is? Maar als dit de bedoeling is - en ik zeg als - dan moet je dat er wél bij zeggen. Geef je je eigen leerlingen ook van dit soort non-opgaven? Fijne docent ben je dan.quote:Op maandag 23 februari 2015 19:13 schreef Borizzz het volgende:
[..]
Ik kwam hem tegen op FB; een post van de docentenopleiding aan de FLOT.


Pardon? Je hoeft me niet zo aan te vallen!quote:Op maandag 23 februari 2015 20:24 schreef Riparius het volgende:
[..]
Het is volslagen onduidelijk wat de opgave is. Wellicht is het de bedoeling om gehele waarden te vinden voor x, y en z zodanig dat de uitdrukking op de tweede regel eveneens geheel is? Maar als dit de bedoeling is - en ik zeg als - dan moet je dat er wél bij zeggen. Geef je je eigen leerlingen ook van dit soort non-opgaven? Fijne docent ben je dan.
Zoals ik al zei, kwam ik dit op Facebook tegen. Het was een post van de fontys lerarenopleiding tilburg. Aangezien ik zelf niks met die opgave kon (maar wel benieuwd was naar een antwoord) postte ik hem hier, in de hoop dat een van jullie wel tot een antwoord kon komen,
kloep kloep


Snap je de vraag zelf?quote:Op maandag 23 februari 2015 20:34 schreef Borizzz het volgende:
[..]
Pardon? Je hoeft me niet zo aan te vallen!
Zoals ik al zei, kwam ik dit op Facebook tegen. Het was een post van de fontys lerarenopleiding tilburg. Aangezien ik zelf niks met die opgave kon (maar wel benieuwd was naar een antwoord) postte ik hem hier, in de hoop dat een van jullie wel tot een antwoord kon komen,


Het enige wat ik lees is dat je niets met de opgave kunt, maar ik lees nergens of je de vraag zelf snapt. Misschien snap je de vraag maar kan je het niet oplossen.quote:Op maandag 23 februari 2015 22:08 schreef Borizzz het volgende:
[..]
Lees jij wel eens posts van users?


Slechte dag gehad?quote:Op maandag 23 februari 2015 20:24 schreef Riparius het volgende:
[..]
Het is volslagen onduidelijk wat de opgave is. Wellicht is het de bedoeling om gehele waarden te vinden voor x, y en z zodanig dat de uitdrukking op de tweede regel eveneens geheel is? Maar als dit de bedoeling is - en ik zeg als - dan moet je dat er wél bij zeggen. Geef je je eigen leerlingen ook van dit soort non-opgaven? Fijne docent ben je dan.
Opinion is the medium between knowledge and ignorance (Plato)


Alleen op het punt dat de opgave niet helder is. De rest verzint hij er ter plekke bij en is onnodig lomp.quote:
Opinion is the medium between knowledge and ignorance (Plato)


Dat ik er ter plekke dingen bij heb verzonnen klopt als een bus. Dat dit onnodig lomp zou zijn is jouw perceptie. Maar wat verwacht je anders als iemand aan komt zetten met een evident incomplete opgave zonder enige moeite te doen om de kennelijk ontbrekende informatie aan te vullen en ik een poging doe om daar toch nog chocola van te maken?quote:Op maandag 23 februari 2015 23:30 schreef Janneke141 het volgende:
[..]
Alleen op het punt dat de opgave niet helder is. De rest verzint hij er ter plekke bij en is onnodig lomp.
Het leek mij gezien de volkomen kwadraten 49, 64 en 81 onder de worteltekens duidelijk dat je iets met Pythagoreïsche tripletten moest doen. De som van de drie vierkantswortels kun je opvatten als de som van drie hypotenusae van drie rechthoekige driehoeken waarvan de rechthoekszijden resp. x en 7, y en 8 en z en 9 zijn. Als je aanneemt dat deze drie rechthoekige driehoeken gelijkvormig zijn dan is de som van deze hypotenusae de hypotenusa van een grotere rechthoekige driehoek met rechthoekszijden x + y + z = 7 en 7 + 8 + 9 = 24, zodat de hypotenusa van de grote rechthoekige driehoek dus 25 zou moeten zijn. Goed, nu hebben we dus
en de oplossing van dit stelsel is
Nu mag je zelf even narekenen dat we inderdaad hebben


Of het nu jouw vak is of niet, je neemt in dit topic de rol van leraar aan. Dan verwacht ik dat je ook op een nette manier om kan gaan met 'leerlingen' die een in jouw perceptie domme vraag stellen. Het zou je in ieder geval sieren.quote:Op dinsdag 24 februari 2015 01:33 schreef Riparius het volgende:
Dat ik er ter plekke dingen bij heb verzonnen klopt als een bus. Dat dit onnodig lomp zou zijn is jouw perceptie. Maar wat verwacht je anders als iemand aan komt zetten met een evident incomplete opgave zonder enige moeite te doen om de kennelijk ontbrekende informatie aan te vullen en ik een poging doe om daar toch nog chocola van te maken?
Het is op zijn zachtst gezegd ironisch dat jij in jouw post aan een ander moet vragen 'wat voor docent hij wel niet is'.
Opinion is the medium between knowledge and ignorance (Plato)


En daarnaast heb ik ook nooit gezegd dat jij antwoord moet geven. Dat jij je daartoe geroepen voelt is jouw zaak.
Ik was met name geïnteresseerd in de inhoudelijke discussie die kan ontstaan naar aanleiding van dit (incomplete) vraagstuk.
Maar goed, OT maar weer.
Ik was met name geïnteresseerd in de inhoudelijke discussie die kan ontstaan naar aanleiding van dit (incomplete) vraagstuk.
Maar goed, OT maar weer.
kloep kloep


Ik wil even benadrukken dat ik vermoed dat Riparius de 'je' als in 'men' bedoelde, dus niet specifiek op de persoon waarop hij reageerde maar in het algemeen. Riparius viel in mijn ogen de persoon aan die de post op Facebook geplaatst had, terecht overigens, maar daar heeft Borizzz weinig aan.quote:Op dinsdag 24 februari 2015 07:47 schreef Janneke141 het volgende:
[..]
Of het nu jouw vak is of niet, je neemt in dit topic de rol van leraar aan. Dan verwacht ik dat je ook op een nette manier om kan gaan met 'leerlingen' die een in jouw perceptie domme vraag stellen. Het zou je in ieder geval sieren.
Het is op zijn zachtst gezegd ironisch dat jij in jouw post aan een ander moet vragen 'wat voor docent hij wel niet is'.


Ik zou hiervoor geogebra gebruiken.quote:Op dinsdag 24 februari 2015 12:24 schreef RRuben het volgende:
Weet iemand een goed en gratis programma om cirkel meetkunde enzo op de computer te doen? Ik kan misschien we paint () gebruiken maar dat gaat denk ik niet zo goed werken.
Edit: om zulke dingen te maken:
[ afbeelding ]
kloep kloep


Ik zie niet hoe het posten van overduidelijk incomplete vraagstukken zou kunnen leiden tot inhoudelijk interessante discussies. Het is evident dat je gisteren maar een deel van het vraagstuk hebt gepost. Even verder spitten levert nog het volgende plaatje op, nota bene in hetzelfde handschrift en op hetzelfde type papier:quote:Op dinsdag 24 februari 2015 09:07 schreef Borizzz het volgende:
En daarnaast heb ik ook nooit gezegd dat jij antwoord moet geven. Dat jij je daartoe geroepen voelt is jouw zaak.
Ik was met name geïnteresseerd in de inhoudelijke discussie die kan ontstaan naar aanleiding van dit (incomplete) vraagstuk.
Maar goed, OT maar weer.
I rest my case.


Dankje! ziet er prima uit!quote:Op dinsdag 24 februari 2015 12:33 schreef Borizzz het volgende:
[..]
Ik zou hiervoor geogebra gebruiken.
leef de leven


Nee. Dit plaatje werd vanmorgen gepost onder het flot account op Facebook. Als oplossing van het vraagstuk (het eerste papiertje) dat gisteren op Facebook werd gezet.quote:Op dinsdag 24 februari 2015 13:06 schreef Riparius het volgende:
[..]
Ik zie niet hoe het posten van overduidelijk incomplete vraagstukken zou kunnen leiden tot inhoudelijk interessante discussies. Het is evident dat je gisteren maar een deel van het vraagstuk hebt gepost. Even verder spitten levert nog het volgende plaatje op, nota bene in hetzelfde handschrift en op hetzelfde type papier:
[ afbeelding ]
I rest my case.
kloep kloep


Je ziet dat hier gebruik wordt gemaakt van de additionele aanname x : y : z = 7 : 8 : 9, precies zoals in de oplossing die ik afgelopen nacht al heb gegeven. Zonder deze of een andere additionele aanname is er geen eenduidige oplossing en is het vraagstuk dus onvolledig.quote:Op dinsdag 24 februari 2015 14:07 schreef Borizzz het volgende:
[..]
Nee. Dit plaatje werd vanmorgen gepost onder het flot account op Facebook. Als oplossing van het vraagstuk (het eerste papiertje) dat gisteren op Facebook werd gezet.


Iemand stuurde mij de onderstaande vraag (de 7200 en 4500 zijn in mm). Mijn antwoord, 2700m, werd niet geaccepteerd omdat de langste zijde van het gebouw waar de buis uit komt maar 250m lang is, dus dan is de uitkomst onrealistisch groot. Iemand die hier iets zinnigs over kan zeggen? 
[ Bericht 1% gewijzigd door #ANONIEM op 25-02-2015 21:44:50 ]
[ Bericht 1% gewijzigd door #ANONIEM op 25-02-2015 21:44:50 ]


hmm raar, ik zou ook 2700m zeggen. Weet je misschien wat het goede antwoord is? Dan kan je kijken waar je een beetje naar toe moet werken.quote:Op woensdag 25 februari 2015 21:42 schreef 2thmx het volgende:
Iemand stuurde mij de onderstaande vraag (de 7200 en 4500 zijn in mm). Mijn antwoord, 2700m, werd niet geaccepteerd omdat de langste zijde van het gebouw waar de buis uit komt maar 250m lang is, dus dan is de uitkomst onrealistisch groot. Iemand die hier iets zinnigs over kan zeggen?
[ afbeelding ]
leef de leven


Als je met dat vervalpercentage niet kan marchanderen (zoals verticale stukken inbouwen) dan kun je dat hoogteverschil niet overbruggen met een kortere leiding. Maar ik heb geen kennis van bouwkundige technieken. Met gaten in gebouwen die op resp. 72 en 45 meter zitten, zijn het trouwens beste fabrieken. De Sint Steven haalt het niet, qua hoogte.
Opinion is the medium between knowledge and ignorance (Plato)


7,2 meter en 4,5 meter  . Mijn tip was ook om met 't hellingspercentage te spelen, maar schijnt niet te kunnen (er zit koelwater in ofzo). Het 'goede antwoord' ken ik niet, het schijnt een soort van realistische situatie te zijn die zijzelf heeft geabstraheerd tot het bovenstaande. Maar ja, bedankt voor de reacties, zal doorgeven dat 't toch echt 2700 meter is met deze gegevens
. Mijn tip was ook om met 't hellingspercentage te spelen, maar schijnt niet te kunnen (er zit koelwater in ofzo). Het 'goede antwoord' ken ik niet, het schijnt een soort van realistische situatie te zijn die zijzelf heeft geabstraheerd tot het bovenstaande. Maar ja, bedankt voor de reacties, zal doorgeven dat 't toch echt 2700 meter is met deze gegevens  .
.
[ Bericht 7% gewijzigd door #ANONIEM op 25-02-2015 22:18:40 ]
[ Bericht 7% gewijzigd door #ANONIEM op 25-02-2015 22:18:40 ]


Kuch. Oeps. Millimeters.quote:Op woensdag 25 februari 2015 22:17 schreef 2thmx het volgende:
7,2 meter en 4,5 meter. Mijn tip was ook om met 't hellingspercentage te spelen, maar schijnt niet te kunnen (er zit koelwater in ofzo). Het 'goede antwoord' ken ik niet, het schijnt een soort van realistische situatie te zijn die zijzelf heeft geabstraheerd tot het bovenstaande. Maar ja, bedankt voor de reacties, zal doorgeven dat 't toch echt 2700 meter is met deze gegevens
.
Opinion is the medium between knowledge and ignorance (Plato)


Nee. Je tekent allemaal lijnen door de oorsprong, en op de voorwaarden x≥0 en y≥0 na, horen ze daar helemaal niet te zitten.quote:
Voorbeeld: de voorwaarde x - y ≤ 2. De lijn x - y = 2 is de rechte door de punten (2,0) en (0,-2). De punten die aan de voorwaarde voldoen, liggen links/boven die lijn.
Opinion is the medium between knowledge and ignorance (Plato)


Maar klopt het dat het geen oplossing heeft doordat groene gebied? Ziet het gebied er zo uit, even de slechte schets wegkijkend?quote:Op donderdag 26 februari 2015 19:28 schreef Janneke141 het volgende:
[..]
Nee. Je tekent allemaal lijnen door de oorsprong, en op de voorwaarden x≥0 en y≥0 na, horen ze daar helemaal niet te zitten.
Voorbeeld: de voorwaarde x - y ≤ 2. De lijn x - y = 2 is de rechte door de punten (2,0) en (0,-2). De punten die aan de voorwaarde voldoen, liggen links/boven die lijn.


Er is maar één relevante overeenkomst tussen jouw schets en het echte plaatje, en dat is dat het groene gebied aan de rechterkant onbegrensd is. Daardoor is er inderdaad geen maximum aan je doelfunctie.quote:Op donderdag 26 februari 2015 20:25 schreef RustCohle het volgende:
[..]
Maar klopt het dat het geen oplossing heeft doordat groene gebied? Ziet het gebied er zo uit, even de slechte schets wegkijkend?
Maar volgens mij heb je geen idee wat je getekend hebt in je schets. Dat heeft niets te maken met netheid, maar met het op de juiste plek en in de juiste richting kunnen tekenen van die lijnen. Ik zou daar nog eens goed naar kijken, als ik jou was.
Opinion is the medium between knowledge and ignorance (Plato)


Als je de voorwaarden herschrijft als functie van y, dan krijg je:quote:Op donderdag 26 februari 2015 20:25 schreef RustCohle het volgende:
[..]
Maar klopt het dat het geen oplossing heeft doordat groene gebied? Ziet het gebied er zo uit, even de slechte schets wegkijkend?
y >= x - 2
y <= 2x + 1
y <= x + 3
Grafisch zoiets:
Herschrijf je de functie die je moet maximaliseren naar y, dan krijg je: y = 2x - c/2
Je wil een zo hoog mogelijke C; bij een hogere C wordt het snijpunt met de y-as lager, maar doordat de rc van deze lijn (rc=2) groter is dan die van de twee grenzen van het 'open' gebied (rc=1), zal de lijn voor elke C (groter dan -2) door het toegestane gebied gaan.
Uit algemene interesse, bij welke studie horen de opgaven die je hier post eigenlijk?


Wo Economiequote:Op donderdag 26 februari 2015 20:50 schreef 2thmx het volgende:
[..]
Als je de voorwaarden herschrijft als functie van y, dan krijg je:
y >= x - 2
y <= 2x + 1
y <= x + 3
Grafisch zoiets:
[ afbeelding ]
Herschrijf je de functie die je moet maximaliseren naar y, dan krijg je: y = 2x - c/2
Je wil een zo hoog mogelijke C; bij een hogere C wordt het snijpunt met de y-as lager, maar doordat de rc van deze lijn (rc=2) groter is dan die van de twee grenzen van het 'open' gebied (rc=1), zal de lijn voor elke C (groter dan -2) door het toegestane gebied gaan.
Uit algemene interesse, bij welke studie horen de opgaven die je hier post eigenlijk?


Je ziet dat er rechts sinc met een c staat en geen sin? Het is de definitie van sinc.quote:Op zaterdag 28 februari 2015 22:39 schreef Bram_van_Loon het volgende:
Waarom geldt deze gelijkheid?
[ afbeelding ]
Voor de duidelijkheid, het invullen van de integraal is uiteraard geen probleem, het is de stap daarna die ik niet volg.


Dat begrijp ik ook wel, het gaat om het eerste =-teken, waarom is de ingevulde integraal gelijk aan die sin(pi*f)/(pi*f)?quote:Op zaterdag 28 februari 2015 22:54 schreef Anoonumos het volgende:
[..]
Je ziet dat er rechts sinc met een c staat en geen sin? Het is de definitie van sinc.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL


mag ik vragen welk programma dat is?quote:Op dinsdag 17 februari 2015 20:59 schreef Janneke141 het volgende:
[..]
Ik ben oprecht benieuwd wat je dan getekend hebt. Bij mij ziet het er in ieder geval zo uit:
[ afbeelding ]
Het gele gebied valt binnen de grenzen. Je doelfunctie is van de vorm x2 = -x1/4 + C, en het is niet moeilijk te zien op welk hoekje van het gele gebied die komt te liggen voor C maximaal.


Zou iemand kunnen controleren of ik op de juiste weg zit?
A) Bij a=2 is de matrix inderdaad inconsistent, maar bij bijv. a= -2 en b=0 ook niet, waardoor deze stelling niet voldoet aan het 'slechts als' voorwaarde.
B) Dan is de matrix juist wel consistent.
C) Klopt.
D) Hij is inconsistent voor elke b indien a=2, dus niet slechts voor b!=0.
A) Bij a=2 is de matrix inderdaad inconsistent, maar bij bijv. a= -2 en b=0 ook niet, waardoor deze stelling niet voldoet aan het 'slechts als' voorwaarde.
B) Dan is de matrix juist wel consistent.
C) Klopt.
D) Hij is inconsistent voor elke b indien a=2, dus niet slechts voor b!=0.











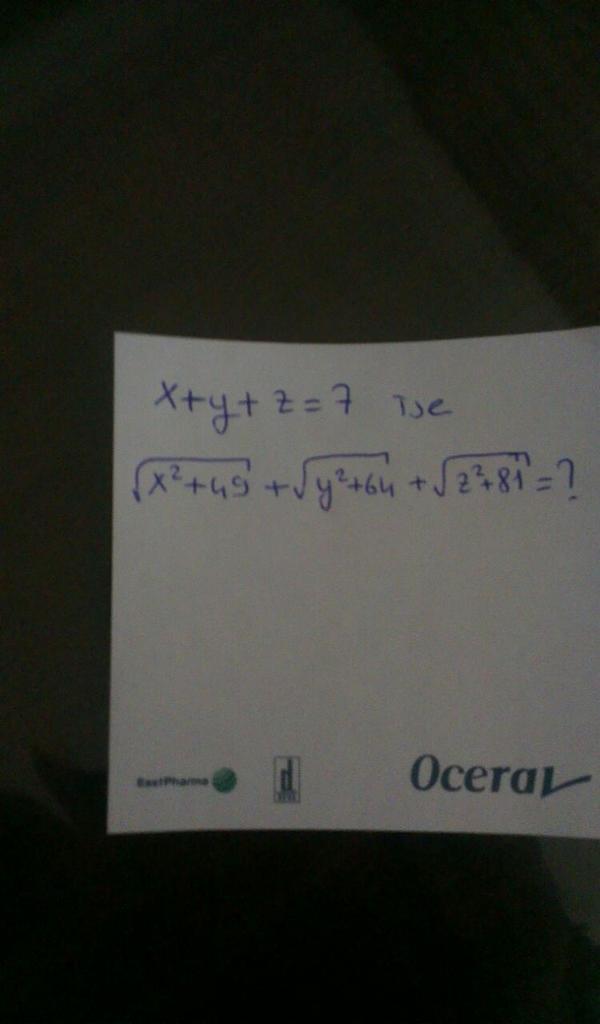







 Op
Op 