SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
Hallo,
Het is al een tijd geleden dat ik wat in dit topic had gevraagd, maar nu heb ik toch wel weer wat vragen. Komende week heb ik een tentamen en de basics begrijp ik onderhand wel, echter zijn de wat 'harder problems' een probleem voor mij. In plaats van het topic vol te spammen met posts met vragen, heb ik besloten om al mijn vragen in één post te verwerken:
Van het volgende snap ik niet waar ik moet beginnen en wat de bedoeling is.. met 'implies that..''
a-1b-1 c-1 = 1/4 implies (abc)4 =
Van het volgende ben ik ten einde raad vanwege de -c...
''Show that the division below leaves a remainder for all values of c''
(x4 + 3x² + 5) : (x-c)
''Solve the following equations'' --> ik weet niet wat ik moet doen als er een ln bij staat... Zelf dacht ik om gewoon te bepalen wanneer x = 0 en de ln even wegdenkend, maar dat werkte dus niet..
ln[x(x-2)] = 0
x ln(x+3) / (x² + 1) = 0
en tenslotte:
ln√(x-5) = 0
[ Bericht 1% gewijzigd door Super-B op 13-09-2014 12:34:01 ]
Het is al een tijd geleden dat ik wat in dit topic had gevraagd, maar nu heb ik toch wel weer wat vragen. Komende week heb ik een tentamen en de basics begrijp ik onderhand wel, echter zijn de wat 'harder problems' een probleem voor mij. In plaats van het topic vol te spammen met posts met vragen, heb ik besloten om al mijn vragen in één post te verwerken:
Van het volgende snap ik niet waar ik moet beginnen en wat de bedoeling is.. met 'implies that..''
a-1b-1 c-1 = 1/4 implies (abc)4 =
Van het volgende ben ik ten einde raad vanwege de -c...
''Show that the division below leaves a remainder for all values of c''
(x4 + 3x² + 5) : (x-c)
''Solve the following equations'' --> ik weet niet wat ik moet doen als er een ln bij staat... Zelf dacht ik om gewoon te bepalen wanneer x = 0 en de ln even wegdenkend, maar dat werkte dus niet..
ln[x(x-2)] = 0
x ln(x+3) / (x² + 1) = 0
en tenslotte:
ln√(x-5) = 0
[ Bericht 1% gewijzigd door Super-B op 13-09-2014 12:34:01 ]
Laatste post vorig topic:
quote:Op zaterdag 13 september 2014 12:20 schreef Janneke141 het volgende:
[..]
Ik heb het gevoel dat de opgave zoals je die hier neerzet niet klopt. Moet het niet toevallig zijn
a-1b-1 c-1 = 1/4 implies (abc) =4
[..]
Ze willen dat je aantoont dat (x-c) geen deler is van het gegeven polynoom, oftewel dat er geen ontbinding te vinden is waarvan (x-c) een van de termen is, voor welke waarde van c dan ook.
Eerder in het topic zijn enkele posts besteed aan het maken van staartdelingen met polynomen, ik denk dat je daarmee deze opgave relatief eenvoudig kan oplossen.
[..]
Voor welk getal q is ln q = 0?
Opinion is the medium between knowledge and ignorance (Plato)
a-1b-1 c-1 = 1/4 implies (abc)4 = ?
Dus ze vragen om (abc)4 uit te rekenen, gegeven dat a-1b-1 c-1 = 1/4.
Lijkt me.
Dus ze vragen om (abc)4 uit te rekenen, gegeven dat a-1b-1 c-1 = 1/4.
Lijkt me.
Exact.. Dus als het één ... is, dan is het ander ...quote:
a-1b-1 c-1 = 1/4 implies (abc)4 = ?
Dus ze vragen om (abc)4 uit te rekenen, gegeven dat a-1b-1 c-1 = 1/4.
Lijkt me.
Polynoom delen is mij wel gelukt, althans bij de opgaven, maar met een -c raak ik echt in de war.quote:
Het lijkt mij dat die -c steeds in de weg zal staan.ln q = 0 wanneer q = 0 denk ik?
e^e = 1
e^0 = 1
Dus eigenlijk spreek ik me tegen dat q = 0, maar verder lijkt mij niet dat er een ander logisch antwoord kan zijn.. e^1 = e..
Gebruik datquote:
[..]
Exact.. Dus als het één ... is, dan is het ander ...
(abc)4 = (a-1b-1c-1)-4
Dus ik moet er gewoon een vergelijking van maken en het dan 'oplossen' ?quote:
[..]
Gebruik dat
(abc)4 = (a-1b-1c-1)-4
Ah ja natuurlijk... maar er stond geen =-teken achter (abc)4quote:
a-1b-1 c-1 = 1/4 implies (abc)4 = ?
Dus ze vragen om (abc)4 uit te rekenen, gegeven dat a-1b-1 c-1 = 1/4.
Lijkt me.
Maar goed.
a-1b-1 c-1 = (abc)-1, en je weet dat dat
(abc)-1 = 4-1.
Dat moet een heel eind voldoende zijn toch?
Opinion is the medium between knowledge and ignorance (Plato)
Kijk nog eens goed terug naar de eigenschappen van de (natuurlijke) logaritme. e0 = 1 klopt, maar dat ee=1 is natuurlijk niet waar.quote:
[..]
Polynoom delen is mij wel gelukt, althans bij de opgaven, maar met een -c raak ik echt in de war.
ln q = 0 wanneer q = 0 denk ik?
e^e = 1
e^0 = 1
Dus eigenlijk spreek ik me tegen dat q = 0, maar verder lijkt mij niet dat er een ander logisch antwoord kan zijn.. e^1 = e..
De (natuurlijke) logaritme is, even kort gezegd, de inverse functie van de e-macht. Dat betekent dat
als ln a = b <=> eb = a
Dus als e0 = 1, dan...
Uit wat hierboven staat volgt trouwens ook dat ln 0 helemaal niet is gedefiniëerd. Er is immers geen enkel getal b waarvoor geldt dat eb = 0
Opinion is the medium between knowledge and ignorance (Plato)
(abc)-1 = 4-1.quote:
[..]
Ah ja natuurlijk... maar er stond geen =-teken achter (abc)4
Maar goed.
a-1b-1 c-1 = (abc)-1, en je weet dat dat
(abc)-1 = 4-1.
Dat moet een heel eind voldoende zijn toch?
(abc)4 = (1/4)-4 dan toch?
Kan dus geschreven worden alsquote:
Ik heb een kwadratische vergelijking met 3 integere variabelen, deze moet geminimaliseerd worden.
Is dit nog analytisch te doen of kan dit alleen opgelost worden door te proberen?
(en misschien is dat ook wel makkelijker)
G = a^2 + b^2 + 2c^2 + ab - 2ca - 2cb
-edit-
G != 0, anders was het niet zo moeilijk
En dan moet ik dus "alle" oplossingen vinden.
G = (a - c)^2 + (b - c)^2 + ab
En G /= 0.
(1, 0, 0) geeft 1 wat dan ook het minimum moet zijn.
Dus dan wordt de vergelijking
(a - c)^2 + (b - c)^2 + ab = 1
-edit-
Alle oplossing zijn denk ik
quote:-1 -1 -1
-1 0 -1
-1 0 0
-1 1 0
0 -1 -1
0 -1 0
0 1 0
0 1 1
1 -1 0
1 0 0
1 0 1
1 1 1
Hmm.. ik weet het niet hoor. Ik begrijp wel wat je bedoeld, maar terugkomend op mijn vragen m.b.t. de ln functies weet ik het niet meer.quote:
[..]
Kijk nog eens goed terug naar de eigenschappen van de (natuurlijke) logaritme. e0 = 1 klopt, maar dat ee=1 is natuurlijk niet waar.
De (natuurlijke) logaritme is, even kort gezegd, de inverse functie van de e-macht. Dat betekent dat
als ln a = b <=> eb = a
Dus als e0 = 1, dan...
Uit wat hierboven staat volgt trouwens ook dat ln 0 helemaal niet is gedefiniëerd. Er is immers geen enkel getal b waarvoor geldt dat eb = 0
We bekijken één van de vergelijkingen die je geeft:quote:
[..]
Hmm.. ik weet het niet hoor. Ik begrijp wel wat je bedoeld, maar terugkomend op mijn vragen m.b.t. de ln functies weet ik het niet meer.
ln[x(x-2)] = 0
ln q = 0 dan en slechts dan als q = 1.
Voor een oplossing van je vergelijking moet dus gelden dat
x(x-2) = 1
Dus x2 - 2x = 1,
Dus (x-1)2 = 2,
Dus x = 1 ± √2
Opinion is the medium between knowledge and ignorance (Plato)
Aha duidelijk, hartstikke bedankt voor je tijd, moeite en uitleg!quote:
[..]
We bekijken één van de vergelijkingen die je geeft:
ln[x(x-2)] = 0
ln q = 0 dan en slechts dan als q = 1.
Voor een oplossing van je vergelijking moet dus gelden dat
x(x-2) = 1
Dus x2 - 2x = 1,
Dus (x-1)2 = 2,
Dus x = 1 ± √2
Ik snap alleen het vetgedrukte niet?
x² - 2x = 1 is toch x(x-2) = 1 --> x = 1 of x = 2?
(x-1)² = x² - 2x + 1 en geen x² - 2x - 1 hoor?
En het kwadraat van 1 is geen 2 hoor..?
Er worden hier altijd vrij veel links naar boeken en dictaten/syllabi geplaatst, misschien handig om deze in de begin post te verzamelen? Eventueel kunnen de uitgebreide posts van Riparius daar ook bij, aangezien deze vaak ook erg nuttig zijn.
Wat ik hier doe is een kwadraat afsplitsen, maar als je die techniek niet kent of niet beheerst raad ik je aan om 'gewoon' de abc-formule toe te passen.quote:
[..]
Aha duidelijk, hartstikke bedankt voor je tijd, moeite en uitleg!
Ik snap alleen het vetgedrukte niet?
x² - 2x = 1 is toch x(x-2) = 1 --> x = 1 of x = 2?
(x-1)² = x² - 2x + 1 en geen x² - 2x - 1 hoor?
Ik voeg even één regeltje toe:
Daarnaast zou ik nog eens even heel goed kijken naarquote:x2 - 2x = 1
x2 - 2x + 1 = 1 + 1
(x-1)2 = 2,
Dus x = 1 ± √2
om er gniffelend achter te komen dat dit natuurlijk helemaal niet klopt.quote:x² - 2x = 1 is toch x(x-2) = 1 --> x = 1 of x = 2?
Opinion is the medium between knowledge and ignorance (Plato)
Ik beheers het kwadraat afsplitsing wel, want mij alleen verbaast is dat je het toepast bij x² - 2x = 1, aangezien de kwadraat afsplitsing meestal gebruikt wordt wanneer de c niet een goed getal is om te factoriseren (toch?).quote:
[..]
Wat ik hier doe is een kwadraat afsplitsen, maar als je die techniek niet kent of niet beheerst raad ik je aan om 'gewoon' de abc-formule toe te passen.
Ik voeg even één regeltje toe:
[..]
Daarnaast zou ik nog eens even heel goed kijken naar
[..]
om er gniffelend achter te komen dat dit natuurlijk helemaal niet klopt.
die 1 komt omdat ln 0 is wanneer ln = 1 toch?
Hoezo? Als het x² - 2x = 0 zou zijn, zou x(x -2)=0 --> x =0 of x = 2 wel van toepassing zijn...quote:
[..]
Wat ik hier doe is een kwadraat afsplitsen, maar als je die techniek niet kent of niet beheerst raad ik je aan om 'gewoon' de abc-formule toe te passen.
Ik voeg even één regeltje toe:
[..]
Daarnaast zou ik nog eens even heel goed kijken naar
[..]
om er gniffelend achter te komen dat dit natuurlijk helemaal niet klopt.
"Hoeveel bedraagt per 1 januari aanstaande de contante waarde van een eeuwigdurende jaarlijkse rente van ¤ 5.000, waarvan de eerste termijn op 1 oktober van het volgend jaar vervalt? De berekening is te baseren op 5 intrest per jaar."
Dat was alles, er is geen aanvullend info. Ik kom er niet uit, of het antwoordmodel is verkeerd. Iemand die mij kan helpen?
Dat was alles, er is geen aanvullend info. Ik kom er niet uit, of het antwoordmodel is verkeerd. Iemand die mij kan helpen?
Kwadraat afsplitsen gebruik ik als er geen eenvoudige ontbinding (x+p)(x+q) te vinden valt, alhoewel het in principe altijd mogelijk is. En ik durf te vermoeden dat jij de ontbinding (x-1+√2)(x-1-√2) niet eenvoudig ziet.quote:
[..]
Ik beheers het kwadraat afsplitsing wel, want mij alleen verbaast is dat je het toepast bij x² - 2x = 1, aangezien de kwadraat afsplitsing meestal gebruikt wordt wanneer de c niet een goed getal is om te factoriseren (toch?).
Het antwoord op wat je bedoelt zal ongetwijfeld 'ja' zijn, maar probeer wat te letten op je wijze van formuleren. Dit lijkt nergens op.quote:die 1 komt omdat ln 0 is wanneer ln = 1 toch?
Probeer je te herinneren waarom je bij het oplossen van (tweedegraads) vergelijkingen altijd eerst ging zorgen dat rechts slechts een =0 overbleef. Dat was omdatquote:
[..]
Hoezo? Als het x² - 2x = 0 zou zijn, zou x(x -2)=0 --> x =0 of x = 2 wel van toepassing zijn...
Als pq=0, dan MOET p=0 OF q=0.
Iets wat voor ieder ander willekeurig getal achter het =-teken natuurlijk nooit geldt.
Als pq=1 dan geldt er helemaal niet dat p=1 of q=1. Wat je opschrijft in post #16 hierboven klopt dus helemaal niet.
[ Bericht 0% gewijzigd door Janneke141 op 13-09-2014 13:45:17 ]
Opinion is the medium between knowledge and ignorance (Plato)
Eens.quote:
Er worden hier altijd vrij veel links naar boeken en dictaten/syllabi geplaatst, misschien handig om deze in de begin post te verzamelen? Eventueel kunnen de uitgebreide posts van Riparius daar ook bij, aangezien deze vaak ook erg nuttig zijn.
Aha.. maar ik begrijp het kwadraat afsplitsen in de deze vraag niet? Er is namelijk geen c?quote:
[..]
Kwadraat afsplitsen gebruik ik als er geen eenvoudige ontbinding (x+p)(x+q) te vinden valt, alhoewel het in principe altijd mogelijk is. En ik durf te vermoeden dat jij de ontbinding (x-1+√2)(x-1-√2) niet eenvoudig ziet.
[..]
Het antwoord op wat je bedoelt zal ongetwijfeld 'ja' zijn, maar probeer wat te letten op je wijze van formuleren. Dit lijkt nergens op.
[..]
Probeer je te herinneren waarom je bij het oplossen van (tweedegraads) vergelijkingen altijd eerst ging zorgen dat rechts slechts een =0 overbleef. Dat was omdat
Als pq=0, dan MOET p=0 OF q=0.
Iets wat voor ieder ander willekeurig getal achter het =-teken natuurlijk nooit geldt.
Als pq=1 dan geldt er helemaal niet dat p=1 of q=1. Wat je opschrijft in post #16 hierboven klopt dus helemaal niet.
Laat maar. Het is mij al duidelijk.quote:
[..]
Aha.. maar ik begrijp het kwadraat afsplitsen in de deze vraag niet? Er is namelijk geen c?
Ik heb nog een vraagje:quote:
[..]
Kwadraat afsplitsen gebruik ik als er geen eenvoudige ontbinding (x+p)(x+q) te vinden valt, alhoewel het in principe altijd mogelijk is. En ik durf te vermoeden dat jij de ontbinding (x-1+√2)(x-1-√2) niet eenvoudig ziet.
[..]
Het antwoord op wat je bedoelt zal ongetwijfeld 'ja' zijn, maar probeer wat te letten op je wijze van formuleren. Dit lijkt nergens op.
[..]
Probeer je te herinneren waarom je bij het oplossen van (tweedegraads) vergelijkingen altijd eerst ging zorgen dat rechts slechts een =0 overbleef. Dat was omdat
Als pq=0, dan MOET p=0 OF q=0.
Iets wat voor ieder ander willekeurig getal achter het =-teken natuurlijk nooit geldt.
Als pq=1 dan geldt er helemaal niet dat p=1 of q=1. Wat je opschrijft in post #16 hierboven klopt dus helemaal niet.
Solve the following equation for x:
3x 4x+2 = 8
Ik had:
3x 4x+2 = 8 wanneer (12)x 42 = 8, and so 12sup]x[/sup] = 1/2
Dus ik had als eindantwoord: x = ln 1/2 / ln 12
Echter zegt het antwoordenboek:
Beide antwoorden zijn correct, immersquote:
[..]
Ik heb nog een vraagje:
Solve the following equation for x:
3x 4x+2 = 8
Ik had:
3x 4x+2 = 8 wanneer (12)x 42 = 8, and so 12sup]x[/sup] = 1/2
Dus ik had als eindantwoord: x = ln 1/2 / ln 12
Echter zegt het antwoordenboek:
[ afbeelding ]
[ afbeelding ]
Aha duidelijk, maar hoe komen ze aan -2 i.p.v. -1/2 ? Ik weet wel dat delen door een breuk vermenigvuldiging met het omgekeerde is, maar dan zou het resulteren tot -1.quote:
[..]
Beide antwoorden zijn correct, immers
[ Bericht 4% gewijzigd door Super-B op 13-09-2014 14:32:23 ]
Kijk eens goed naar de post waar je op reageert.quote:
[..]
Aha duidelijk, maar hoe komen ze aan -2 i.p.v. -1/2 ? Ik weet wel dat delen door een breuk vermenigvuldiging met het omgekeerde is, maar dan zou het resulteren tot -1.
Ja klopt.. Ben alleen benieuwd hoe het antwoordenboek aan -2 komt.quote:Op zaterdag 13 september 2014 14:31 schreef OllieWilliams het volgende:
[..]
Kijk eens goed naar de post waar je op reageert.
quote:
[..]
Ja klopt.. Ben alleen benieuwd hoe het antwoordenboek aan -2 komt.
Nog één voor het oplossen van x:
4x - 4x-1 = 3x+1 - 3x
Ik heb dit herschreven tot:
4x - 4x * 4-1 = 3x * 31 * 3x
Dit resulteert tot:
4-1 = 31 .... De getallen met de exponent x valt dus weg en dit wordt het dan en hier klopt dan ook geen kant van....
[ Bericht 0% gewijzigd door Super-B op 13-09-2014 14:43:35 ]
4x - 4x-1 = 3x+1 - 3x
Ik heb dit herschreven tot:
4x - 4x * 4-1 = 3x * 31 * 3x
Dit resulteert tot:
4-1 = 31 .... De getallen met de exponent x valt dus weg en dit wordt het dan en hier klopt dan ook geen kant van....
[ Bericht 0% gewijzigd door Super-B op 13-09-2014 14:43:35 ]
Van de tweede vergelijking klopt de linkerkant nog.quote:
Nog één voor het oplossen van x:
4x - 4x-1 = 3x+1 - 3x
Ik heb dit herschreven tot:
4x - 4x * 4-1 = 3x * 3-1 3x
Dit resulteert tot:
4-1 = 31 .... De getallen met de exponent x valt dus weg en dit wordt het dan en hier klopt dan ook geen kant van....
Verder niks, wat ben je aan het doen?
welke regels pas je toe?
Ik zou nog eens goed naar de rekenregels voor logaritmen kijken, als je daar goed mee bekend bent is dit een fluitje van een cent.quote:
[..]
Oh zo.. Ja ik interpreteerde het anders...Thanks.
ln 1/2 = ln 2-1 = -1 * ln 2
Oeps aan de rechterkant moet het exponent 1 zijn i.p.v. -1.quote:
[..]
Van de tweede vergelijking klopt de linkerkant nog.
Verder niks, wat ben je aan het doen?
welke regels pas je toe?
Ik dacht ik schrijf ze los van elkaar en dan trek ik de grondgetallen, die hetzelfde zijn, met het exponent x van elkaar af..quote:
[..]
Van de tweede vergelijking klopt de linkerkant nog.
Verder niks, wat ben je aan het doen?
welke regels pas je toe?
Dan is ie nog niet goed.quote:
[..]
Oeps aan de rechterkant moet het exponent 1 zijn i.p.v. -1.
Ik heb wel eens van logaritmes gehoord, maar de materie zelf is nieuw voor mij. Mijn vooropleidingen zijn de havo en het propedeuse jaar van het hbo. Ik zit nu in het eerste jaar van een wo opleiding. De materie die aan bod komt zijn grotendeels nieuw voor me.quote:
[..]
Ik zou nog eens goed naar de rekenregels voor logaritmen kijken, als je daar goed mee bekend bent is dit een fluitje van een cent.
ln 1/2 = ln 2-1 = -1 * ln 2
De FOK!-bibliografie:
Basisschool
Spijkerreeks?
Middelbareschool
Getal en Ruimte
Basisboek wiskunde
Hoger onderwijs
Algemeen/Multidisciplinair
J. Stewart, Calculus, Early Transcendentals, Cengage Learning 2007(?)
C.P. Simon & L. Blume, Mathematics for Economists , W.W. Norton & Company 1994
Analyse
S. Abbot, Understanding Analysis, Springer 2010(?)
T.M. Apostel, Calculus, Vol. II, John Wiley & Sons 1969
Rudin, Principles of Mathematical Analysis
Topologie
Munkres, Topology
Lineaire Algebra
Lay, Linear Algebra and Aplications
H. Minc, Nonnegative Matrices, John Wiley and Sons 1988
P. Lancaster & M. Tismenetsky, The theory of matrices, Academic Press 1985
A. Berman & R.J. Plemmons, Nonnegative matrices in the mathematical sciences, Academic Press 1979
Discrete Wiskunde
R.P. Grimaldi, Discrete and combinatorial mathematics. An applied introduction, Addison-Wesley Publishing Company 1989
Lineair en Niet-Lineair Programmeren
Kansberekening en (Wiskundige) Statistiek
A. Azzalini, Statistical Inference Based on the likelihood, Chapman & Hall/CRC 1996
Miller & Miller, Mathematical Statistics with Applications, (...)
(Mogen we van FOK! links plaatsen naar copyrighted materiaal, dus pdf's van boeken?)
TO DO: Meer boeken, structuur bepalen van verwijzing
Basisschool
Spijkerreeks?
Middelbareschool
Getal en Ruimte
Basisboek wiskunde
Hoger onderwijs
Algemeen/Multidisciplinair
J. Stewart, Calculus, Early Transcendentals, Cengage Learning 2007(?)
C.P. Simon & L. Blume, Mathematics for Economists , W.W. Norton & Company 1994
Analyse
S. Abbot, Understanding Analysis, Springer 2010(?)
T.M. Apostel, Calculus, Vol. II, John Wiley & Sons 1969
Rudin, Principles of Mathematical Analysis
Topologie
Munkres, Topology
Lineaire Algebra
Lay, Linear Algebra and Aplications
H. Minc, Nonnegative Matrices, John Wiley and Sons 1988
P. Lancaster & M. Tismenetsky, The theory of matrices, Academic Press 1985
A. Berman & R.J. Plemmons, Nonnegative matrices in the mathematical sciences, Academic Press 1979
Discrete Wiskunde
R.P. Grimaldi, Discrete and combinatorial mathematics. An applied introduction, Addison-Wesley Publishing Company 1989
Lineair en Niet-Lineair Programmeren
Kansberekening en (Wiskundige) Statistiek
A. Azzalini, Statistical Inference Based on the likelihood, Chapman & Hall/CRC 1996
Miller & Miller, Mathematical Statistics with Applications, (...)
(Mogen we van FOK! links plaatsen naar copyrighted materiaal, dus pdf's van boeken?)
TO DO: Meer boeken, structuur bepalen van verwijzing
Wow... Ik heb hier een hele simpele functie die ik niet weet op te lossen, maar dat komt omdat er zowel links en recht een x staat... en omdat er een +32 staat. Als die +32 er niet stond, kon je gemakkelijk de 6/2 = 3 methode toepassen... toch geprobeerd, maar heb het gevoel alsof het compleet fout is.
''Bereken wat x is'.'
x = 9/5 * x + 32
Simpel te herschrijven tot x = 9x/5 + 32
Vervolgens steeds de 6/2 = 3 methode toepassen en de +32 tijdelijk wegdenken:
9x/x = x/5 + 32
9 = x/5 + 32
x= 9 * 5 + 32
x = 77
''Bereken wat x is'.'
x = 9/5 * x + 32
Simpel te herschrijven tot x = 9x/5 + 32
Vervolgens steeds de 6/2 = 3 methode toepassen en de +32 tijdelijk wegdenken:
9x/x = x/5 + 32
9 = x/5 + 32
x= 9 * 5 + 32
x = 77
x - (9/5)x = 32quote:
Wow... Ik heb hier een hele simpele functie die ik niet weet op te lossen, maar dat komt omdat er zowel links en recht een x staat... en omdat er een +32 staat. Als die +32 er niet stond, kon je gemakkelijk de 6/2 = 3 methode toepassen... toch geprobeerd, maar heb het gevoel alsof het compleet fout is.
''Bereken wat x is'.'
x = 9/5 * x + 32
Simpel te herschrijven tot x = 9x/5 + 32
Vervolgens steeds de 6/2 = 3 methode toepassen en de +32 tijdelijk wegdenken:
9x/x = x/5 + 32
9 = x/5 + 32
x= 9 * 5 + 32
x = 77
-(4/5)x = 32
x = -40
Had ik moeten weten.quote:
[..]
x - (9/5)x = 32
-(4/5)x = 32
x = -40
Welke rekenregel zou je daarvoor willen toepassen?quote:
[..]
Ik dacht ik schrijf ze los van elkaar en dan trek ik de grondgetallen, die hetzelfde zijn, met het exponent x van elkaar af..
Opinion is the medium between knowledge and ignorance (Plato)
Geen idee.quote:
[..]
Welke rekenregel zou je daarvoor willen toepassen?
Schrijf het nog eens op, want ik heb nu geen idee waar je het over hebt.quote:
[..]
Vermenigvuldigingsteken moest tussen de laatste twee grondgetallen (3).
En zet er ook eens bij welke regel je gebruikt.
Ik betwijfel of je het wel begrijpt. De vergelijking x² − 2x = 1 is niet (eenvoudig) op te lossen via ontbinden in factoren maar juist prima via kwadraatafsplitsing (die overigens altijd toepasbaar is om een vierkantsvergelijking op te lossen). Ik wil je sterk aanbevelen deze recente post van mij eens goed door te nemen.quote:
[..]
Ik beheers het kwadraat afsplitsing wel, want mij alleen verbaast is dat je het toepast bij x² - 2x = 1, aangezien de kwadraat afsplitsing meestal gebruikt wordt wanneer de c niet een goed getal is om te factoriseren (toch?).
Ik begrijp wat je wil zeggen maar zo mag je dit niet opschrijven. Je bedoelt te zeggen dat ln x = 0 equivalent is met x = 1, dus zeg dat dan ook.quote:die 1 komt omdat ln 0 is wanneer ln = 1 toch?
Een logaritme van een gegeven getal is niets anders dan een exponent, namelijk de exponent waartoe je een vast getal (het grondtal van de logaritme) moet verheffen om het gegeven getal te verkrijgen. Voor de natuurlijke logaritme, aangegeven met het functiesymbool ln (dat staat voor logarithmus naturalis) is het grondtal het bijzondere getal e. Het getal e is zo bijzonder omdat e het enige (positieve, reële) getal is waarvoor geldt dat de grafiek van f(x) = ex in elk punt precies even steil loopt als de functiewaarde voor dat punt aangeeft. De functie f(x) = ex heeft dus zichzelf als afgeleide.
De uitspraak
ln x = y
betekent niets anders dan dat y de exponent is waartoe we e moeten verheffen om x te krijgen, dus
ey = x
Zo zie je gemakkelijk dat ln 1 = 0, want 0 is immers de exponent waartoe we e moeten verheffen om 1 te krijgen: e0 = 1. Ook zie je zo gemakkelijk dat ln e = 1, want we moeten e tot de macht 1 verheffen om e te krijgen: e1 = e.
Alle rekenregels die gelden voor het werken met logaritmen volgen gemakkelijk uit de rekenregels voor het werken met machten, want een logaritme is immers niets anders dan een exponent.
Heb je bijvoorbeeld
ln a = p, ln b = q
dan betekent dit
ep = a, eq = b
Maar dan is dus ook
ep·eq = ab
En omdat exponenten optellen bij het vermenigvuldigen van twee machten met hetzelfde grondtal hebben we dus
ep+q = ab
Maar als het zo is dat je e moet verheffen tot de macht p + q om ab te krijgen, dan betekent dit niets anders dan dat de natuurlijke logaritme van ab gelijk is aan p + q, dus
ln ab = p + q
Maar nu is p = ln a en q = ln b zodat we dus hebben
ln ab = ln a + ln b
Je ziet dus dat de bekende regel die zegt dat de (natuurlijke) logaritme van een product van twee (positieve, reële) getallen gelijk is aan de som van de (natuurlijke) logaritmen van elk van de factoren niets anders is dan een andere gedaante van de regel die zegt dat exponenten optellen bij vermenigvuldiging van twee machten van hetzelfde grondtal. Op een soortgelijke manier zijn ook alle andere rekenregels voor logaritmen af te leiden uit rekenregels voor het werken met machten.
[ Bericht 0% gewijzigd door Riparius op 13-09-2014 21:50:51 ]
Dit is al fout, want je had in het rechterlid een product waar je een minteken moet hebben, maar dit zal wellicht een verschrijving zijn (die niettemin verraadt dat je niet zorgvuldig genoeg werkt).quote:
Nog één voor het oplossen van x:
4x - 4x-1 = 3x+1 - 3x
Ik heb dit herschreven tot:
4x - 4x * 4-1 = 3x * 31 - 3x
Nee jongeman, dit lijkt nergens op. Je begon nochtans goed (afgezien van die verschrijving).quote:Dit resulteert tot:
[cut crap]
Als je links een factor 4x buiten haakjes haalt en rechts een factor 3x buiten haakjes haalt dan krijg je
4x(1 − 4−1) = 3x(3 − 1)
Nu mag je eens even gaan nadenken hoe je verder kunt gaan.
Super-B, als ik jou was zou ik eens gaan inversteren in bijles of een cursus. Want je mist gewoon zoveel basiskennis. Ik weet niet welke studie je doet, maar als je zo door gaat vrees ik het ergste voor je.
Bedankt voor de tip, maar ik vind het tot nu toe vrij goed te doen met zelfstudie en dit topic.quote:
Super-B, als ik jou was zou ik eens gaan inversteren in bijles of een cursus. Want je mist gewoon zoveel basiskennis. Ik weet niet welke studie je doet, maar als je zo door gaat vrees ik het ergste voor je.
Gelukkig behoren de vragen die ik stel tot de stof van het tentamen voor volgende week en behoren ze volgens het boek tot 'harder problems'. De basic-opgaven gaan mij wel makkelijk af.
Echter is er nog veel werk te doen om de kennis goed te beheersen, maar ik denk dat het tentamen wel te doen is.De stof van het (deel)tentamen is het volgende:
De onderwerpen die ik tot nu toe nog wel pittig vind zijn:
-Logartime (niet de regels, maar de wat moeilijkere opgaven met log, ln en/of het getal e)
-Polynomen en staartdelingen.
-Afgeleiden (nieuwe materie voor mij)
-Regels voor differentiëren (ook nieuwe materie voor mij).
Inverse functies en samengestelde functies zijn ook nieuw voor mij, echter begrijp ik het tot dusverre wel.
Voor velen in dit topic is dit een eitje en zullen mijn vragen dan ook niet de moeilijkste zijn, maar het gaat tot nu toe wel goed met leren (met hier en daar nog wat slordigheidsfoutjes en wat fouten waaraan te zien is dat ik het nog niet goed beheers).
Dank voor de zéér, maar dan ook zéér duidelijke uitleg.quote:
[..]
Ik betwijfel of je het wel begrijpt. De vergelijking x² − 2x = 1 is niet (eenvoudig) op te lossen via ontbinden in factoren maar juist prima via kwadraatafsplitsing (die overigens altijd toepasbaar is om een vierkantsvergelijking op te lossen). Ik wil je sterk aanbevelen deze recente post van mij eens goed door te nemen.
[..]
Ik begrijp wat je wil zeggen maar zo mag je dit niet opschrijven. Je bedoelt te zeggen dat ln x = 0 equivalent is met x = 1, dus zeg dat dan ook.
Een logaritme van een gegeven getal is niets anders dan een exponent, namelijk de exponent waartoe je een vast getal (het grondtal van de logaritme) moet verheffen om het gegeven getal te verkrijgen. Voor de natuurlijke logaritme, aangegeven met het functiesymbool ln (dat staat voor logarithmus naturalis) is het grondtal het bijzondere getal e. Het getal e is zo bijzonder omdat e het enige (positieve, reële) getal is waarvoor geldt dat de grafiek van f(x) = ex in elk punt precies even stijl loopt als de functiewaarde voor dat punt aangeeft. De functie f(x) = ex heeft dus zichzelf als afgeleide.
De uitspraak
ln x = y
betekent niets anders dan dat y de exponent is waartoe we e moeten verheffen om x te krijgen, dus
ey = x
Zo zie je gemakkelijk dat ln 1 = 0, want 0 is immers de exponent waartoe we e moeten verheffen om 1 te krijgen: e0 = 1. Ook zie je zo gemakkelijk dat ln e = 1, want we moeten e tot de macht 1 verheffen om e te krijgen: e1 = e.
Alle rekenregels die gelden voor het werken met logaritmen volgen gemakkelijk uit de rekenregels voor het werken met machten, want een logaritme is immers niets anders dan een exponent.
Heb je bijvoorbeeld
ln a = p, ln b = q
dan betekent dit
ep = a, eq = b
Maar dan is dus ook
ep·eq = ab
En omdat exponenten optellen bij het vermenigvuldigen van twee machten met hetzelfde grondtal hebben we dus
ep+q = ab
Maar als het zo is dat je e moet verheffen tot de macht p + q om ab te krijgen, dan betekent dit niets anders dan dat de natuurlijke logaritme van ab gelijk is aan p + q, dus
ln ab = p + q
Maar nu is p = ln a en q = ln b zodat we dus hebben
ln ab = ln a + ln b
Je ziet dus dat de bekende regel die zegt dat de (natuurlijke) logaritme van een product van twee (positieve, reële) getallen gelijk is aan de som van de (natuurlijke) logaritmen van elk van de factoren niets anders is dan een andere gedaante van de regel die zegt dat exponenten optellen bij vermenigvuldiging van twee machten van hetzelfde grondtal. Op een soortgelijke manier zijn ook alle andere rekenregels voor logaritmen af te leiden uit rekenregels voor het werken met machten.
"Verschuif de lijn m over de vector p = OP→ en noem de verschoven lijn l."
Wat wordt bedoeld met verschuiven? Alleen in x/y richting verschuiven? Of ook z?.
Wat wordt bedoeld met verschuiven? Alleen in x/y richting verschuiven? Of ook z?.
Onzin, je hebt voor de zomervakantie een paar maanden lang allemaal vragen gepost over differentiëren. Weet je nog, met de ketting/product/som/quotiëntregel?quote:
[..]
Bedankt voor de tip, maar ik vind het tot nu toe vrij goed te doen met zelfstudie en dit topic.
Gelukkig behoren de vragen die ik stel tot de stof van het tentamen voor volgende week en behoren ze volgens het boek tot 'harder problems'. De basic-opgaven gaan mij wel makkelijk af.
De stof van het (deel)tentamen is het volgende:
[ afbeelding ]
De onderwerpen die ik tot nu toe nog wel pittig vind zijn:
-Logartime (niet de regels, maar de wat moeilijkere opgaven met log, ln en/of het getal e)
-Polynomen en staartdelingen.
-Afgeleiden (nieuwe materie voor mij)
-Regels voor differentiëren (ook nieuwe materie voor mij).
Inverse functies en samengestelde functies zijn ook nieuw voor mij, echter begrijp ik het tot dusverre wel.
Voor velen in dit topic is dit een eitje en zullen mijn vragen dan ook niet de moeilijkste zijn, maar het gaat tot nu toe wel goed met leren (met hier en daar nog wat slordigheidsfoutjes en wat fouten waaraan te zien is dat ik het nog niet goed beheers).
Riparius had hem ook al verteld dat hij de Spijkerreeks moet kopen, een tijd terug, of dat was tegen een andere hbo'er die ook economie wilde gaan doen. Anyhow, dat heeft diegene ook niet gedaan.quote:
Super-B, als ik jou was zou ik eens gaan inversteren in bijles of een cursus. Want je mist gewoon zoveel basiskennis. Ik weet niet welke studie je doet, maar als je zo door gaat vrees ik het ergste voor je.
Iets meer context?quote:
"Verschuif de lijn m over de vector p = OP→ en noem de verschoven lijn l."
Wat wordt bedoeld met verschuiven? Alleen in x/y richting verschuiven? Of ook z?.
Een vector is een gericht lijnstuk (of een equivalentieklasse van gerichte lijnstukken met dezelfde lengte en dezelfde richting) en een vector definieert aldus een translatie. Als je niet vertelt welke vector je vector p = OP is, dan is je vraag ook niet te beantwoorden.quote:
"Verschuif de lijn m over de vector p = OP→ en noem de verschoven lijn l."
Wat wordt bedoeld met verschuiven? Alleen in x/y richting verschuiven? Of ook z?.
quote:
Paragraaf 1.2: http://www.staff.science.(...)inalg2013dictaat.pdfquote:
[..]
Een vector is een gericht lijnstuk (of een equivalentieklasse van gerichte lijnstukken met dezelfde lengte en dezelfde richting) en een vector definieert aldus een translatie. Als je niet vertelt welke vector je vector p = OP is, dan is je vraag ook niet te beantwoorden.
Zoals ik het interpreteer in alle dimensies. De verzamelingquote:
[..]
[..]
Paragraaf 1.2: http://www.staff.science.(...)inalg2013dictaat.pdf
OK, dus als je een voorbeeld maakt, zou het er zo uit kunnen zien? https://www.dropbox.com/s(...)oorstelling.png?dl=0quote:
[..]
Zoals ik het interpreteer in alle dimensies. De verzamelingmoet je zien als alle evenwijdige lijnen van de vector
.
Teken gewoon eens een plaatje, in een plat vlak om het simpel te houden. Kies een punt O (als oorsprong) en een punt A ≠ O en teken vector OA = a, dan is elk punt op de rechte door O en A het eindpunt van een vector v = λa voor een zekere λ ∈ R, en als je λ de verzameling R van alle reële getallen laat doorlopen dan krijg je voor het eindpunt van vector v = λa elk punt op de rechte door O en A. We noemen v = λa daarom een vectorvoorstelling van de rechte m door O en A.quote:
[..]
[..]
Paragraaf 1.2: http://www.staff.science.(...)inalg2013dictaat.pdf
Kies vervolgens een willekeurig punt P buiten lijn m en verschuif lijn m dan in één rechte beweging zodanig dat punt O op lijn m in punt P komt te liggen. Dan hebben we als beeld van de rechte lijn m een rechte lijn l door punt P die evenwijdig is aan lijn m. Elk punt op deze lijn l is nu het eindpunt van een vector v = p + λa voor een zekere λ ∈ R, en als je λ weer de verzameling R van alle reële getallen laat doorlopen dan krijg je als eindpunt van vector v = p + λa elk punt op de rechte l door P evenwijdig aan m. Aldus is v = p + λa een vectorvoorstelling van l. Vector a heet een richtingsvector van lijn l en vector p heet een steunvector (ook wel een plaatsvector) van lijn l.
Vóór de zomervakantie. Dat was voor de toelatingstoets wiskunde voor de universiteit. Heb het afgerond met een 7.0. Desondanks blijt de materie nog nieuw voor mij. Het is alweer weggezakt en havo/hbo wiskunde stelt niet zoveel voor.quote:
[..]
Onzin, je hebt voor de zomervakantie een paar maanden lang allemaal vragen gepost over differentiëren. Weet je nog, met de ketting/product/som/quotiëntregel?
Als ik (e0,001 - 1) / 1 invul in mijn rekenmachine krijg ik geen , maar 0,0010005 Doe ik iets fout of..?
Je deelt door 1 ipv x.quote:
[ afbeelding ]
Als ik (e0,001 - 1) / 1 invul in mijn rekenmachine krijg ik geen [ afbeelding ], maar 0,0010005 Doe ik iets fout of..?
Ja, je doet iets fout, en in mijn glazen bol zie ik dat je waarschijnlijk alleen ex − 1 hebt berekend voor x = 0,001. Je bent dus helemaal vergeten dat je het resultaat weer door x moest delen.quote:
[ afbeelding ]
Als ik (e0,001 - 1) / 1 invul in mijn rekenmachine krijg ik geen [ afbeelding ], maar 0,0010005 Doe ik iets fout of..?
quote:
Slordig!quote:
[..]
Ja, je doet iets fout, en in mijn glazen bol zie ik dat je waarschijnlijk alleen ex hebt berekend voor x = 0,001. Je bent dus helemaal vergeten dat je van die ex nog 1 af moest trekken en het resultaat weer door x moest delen.
Thanks!
Wiskunde is echt een heerlijk vak, met name door de uitdaging die er in zit.
Hopelijk zie je ook waarom die limiet van (ex − 1)/x voor x → 0 oftewel de limiet van (eh − 1)/h voor h → 0 nu zo interessant is. Als je de afgeleide gaat bepalen vanquote:
[..]
[..]
Wiskunde is echt een heerlijk vak, met name door de uitdaging die er in zit.
f(x) = ax
voor een a ∈ R+ met behulp van de definitie van de afgeleide, dan krijg je
f'(x) = limh→0 (ax+h − ax)/h
en aangezien ax+h = ax·ah kunnen we een factor ax buiten haakjes halen in de teller van het differentiequotiënt en omdat ax niet afhangt van h kunnen we deze factor ax voor de limiet brengen zodat we kunnen schrijven
f'(x) = ax · limh→0 (ah − 1)/h
Maar omdat 1 = a0 is limh→0 (ah − 1)/h = limh→0 (ah − a0)/h niets anders dan de afgeleide van de functie in het punt x = 0 oftewel f'(0). We vinden voor de functie f(x) = ax dus
f'(x) = f'(0)·ax
Een exponentiële functie heeft dus een afgeleide die weer een exponentiële functie is met datzelfde grondtal, maar dan wel vermenigvuldigd met een constante factor die de steilheid geeft van de grafiek van de functie bij x = 0. En nu blijkt er precies één positief reëel getal a te zijn waarbij de steilheid van de exponentiële curve bij x = 0 precies gelijk is aan 1, en dat getal noemen we e. Voor a = e heb je zo dus
f'(x) = ex
als afgeleide van
f(x) = ex
Natuurlijk wil je nu ook nog weten wat die f'(0) = limh→0 (ah − 1)/h voor een willekeurige (positieve, reële) a nu in het algemeen voorstelt, en dat blijkt niets anders te zijn dan de natuurlijke logaritme van a, dus
limh→0 (ah − 1)/h = ln a
Zo hebben we dus voor
f(x) = ax
met a ∈ R+ in het algemeen als afgeleide
f'(x) = ax·ln a
Okay volgens mij is dit redelijk simpel maar ik zie het gewoon niet, ik hoop dat iemand mij kan helpen.
Is de som: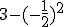
hetzelfde als: 
?
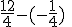Naar mijn inzien namelijk wel maar de antwoorden verschillen. het antwoord van som 1 is namelijk 2,75 en die van som twee 3,25.
Is de som:
Naar mijn inzien namelijk wel maar de antwoorden verschillen. het antwoord van som 1 is namelijk 2,75 en die van som twee 3,25.
Nee, dit is niet hetzelfde. Je negeert namelijk de rekenregel min maal min geeft plus. Het kwadraat van −½ is ¼, niet −¼.quote:
Okay volgens mij is dit redelijk simpel maar ik zie het gewoon niet, ik hoop dat iemand mij kan helpen.
Is de som:
Naar mijn inzien namelijk wel maar de antwoorden verschillen. het antwoord van som 1 is namelijk 2,75 en die van som twee 3,25.
