SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Die min kun je in principe gewoon d.m.v. een soort regel (wat jij postte zojuist) altijd buiten de wortel halen?quote:Op vrijdag 6 juni 2014 18:18 schreef Riparius het volgende:
[..]
Bij onevenmachtswortels kun je binnen de reële getallen wel de wortel nemen van een negatief getal. En aangezien
3√(−1) = −1
heb je dus ook
3√(−12) = 3√((−1)·12) = 3√(−1)·3√12 = −3√12
Breng eerst het minteken vóór het wortelteken, en daarmee vóór de breuk, aangezien a/(−b) = −a/b.quote:
Daarnaast:
5√7 / 5√-27
Hoe ga ik met die -27 om in priemgetallen? Ik wil het ontbinden zodat ik de priemgetallen heb.. Maar moet ik dan gewoon beginnen met -27 / 3 of -27 / -3 ?
Niet altijd, alleen bij onevenmachtswortels. En het is niet een of andere duistere regel, maar gewoon de regelquote:
[..]
Die min kun je in principe gewoon d.m.v. een soort regel (wat jij postte zojuist) altijd buiten de wortel halen?
n√(a·b) = n√a · n√b
Let wel op dat deze regel voor even n alleen geldt als a en b beide niet negatief zijn. Bij oneven n mogen a of b (of beide) wel negatief zijn.
Je bent een held. Dank je wel!quote:
[..]
Niet altijd, alleen bij onevenmachtswortels. En het is niet een of andere duistere regel, maar gewoon de regel
n√(a·b) = n√a · n√b
Let wel op dat deze regel voor even n alleen geldt als a en b beide niet negatief zijn. Bij oneven n mogen a of b (of beide) wel negatief zijn.
Laatste ''wortel''vraag:
Hoe vermenigvuldig/deel je wortels die ongelijk aan elkaar zijn? Gewoon herschrijven naar machtenvorm en vervolgens de regels voor machten toepassen?
Geef eens een voorbeeld en laat zien hoe je dat zelf zou herleiden.quote:
Hoe vermenigvuldig/deel je wortels die ongelijk aan elkaar zijn? Gewoon herschrijven naar machtenvorm en vervolgens de regels voor machten toepassen?
Drie voorbeelden (twee m.b.t. machten en wortels en één m.b.t. ongelijke wortels):quote:
[..]
Geef eens een voorbeeld en laat zien hoe je dat zelf zou herleiden.
1 / (2 4√2) --> 2-1/4 * 2
3 / ²√3 -- > geen idee vanwege die 3 in de teller?
²√2 : ³√2 --> 2-1/2 : 2-1/3 en vervolgens ....dan:
2-1/6 volgens de machtregel van het delen van letters/getallen met machten.
Nee, die factor 2 staat in de noemer van de breuk en is dus 1/2 = 2−1.quote:
[..]
Drie voorbeelden (twee m.b.t. machten en wortels en één m.b.t. ongelijke wortels):
1 / (2 4√2) --> 2-1/4 * 2
1 / (2·4√2) = 2−1·2−1/4 = 2−5/4
Tuurlijk weet je dit wel. 3 = 2√9, dusquote:3 / ²√3 -- > geen idee vanwege die 3 in de teller?
3 / 2√3 = 2√9 / 2√3 = 2√(9/3) = 2√3
Nee. Je hebt voor a > 0quote:²√2 : ³√2 --> 2-1/2 : 2-1/3 en vervolgens ....dan:
2-1/6 volgens de machtregel van het delen van letters/getallen met machten.
n√a = a1/n
en
ap : aq = ap−q
dus
2√2 : 3√2 = 21/2 : 21/3 = 21/2 − 1/3 = 21/6
[ Bericht 0% gewijzigd door Riparius op 07-06-2014 15:21:09 ]
Die tweede begrijp ik geen donder van.quote:
[..]
Nee, die factor 2 staat in de noemer van de breuk en is dus 1/2 = 2−1.
1 / (2·4√2) = 2−1·2−1/4 = 2−5/4
[..]
Tuurlijk weet je dit wel. 3 = 2√9, dus
3 / 2√3 = 2√9 / 2√3 = 2√(9/3) = 2√3
[..]
Nee. Je hebt voor a ≥ 0
n√a = a1/n
en
ap : aq = ap−q
dus
2√2 : 3√2 = 21/2 : 21/3 = 21/2 − 1/3 = 21/6
Ik snap die overgang niet van het begin naar 3 / 2√3
Vierkantswortels komen zo vaak voor dat men de 2 dan meestal weglaat, dus 2√9 is hetzelfde als √9. En je weet toch dat 3 = √9 en ook dat voor a,b > 0 geldtquote:
[..]
Die tweede begrijp ik geen donder van.
√a / √b = √(a/b)
Dus hebben we
3 / √3 = √9 / √3 = √3
Andere manier: vermenigvuldig teller en noemer van 3 / √ 3 met √3, dan krijg je
3 / √3 = 3√3 / 3 = √3
Laat maar heb het al!quote:
[..]
Vierkantswortels komen zo vaak voor dat men de 2 dan meestal weglaat, dus 2√9 is hetzelfde als √9. En je weet toch dat 3 = √9 en ook dat voor a,b > 0 geldt
√a / √b = √(a/b)
Dus hebben we
3 / √3 = √9 / √3 = √3
Andere manier: vermenigvuldig teller en noemer van 3 / √ 3 met √3, dan krijg je
3 / √3 = 3√3 / 3 = √3
Thanks!
Is het ook goed als ik jouw methode voor die tweede gebruik? Dus een deling met wortels oplossen dmv priemgetallen ipv de wortel met hetzelfde wortel te vermenigvuldigen?quote:
[..]
Nee, die factor 2 staat in de noemer van de breuk en is dus 1/2 = 2−1.
1 / (2·4√2) = 2−1·2−1/4 = 2−5/4
[..]
Tuurlijk weet je dit wel. 3 = 2√9, dus
3 / 2√3 = 2√9 / 2√3 = 2√(9/3) = 2√3
[..]
Nee. Je hebt voor a ≥ 0
n√a = a1/n
en
ap : aq = ap−q
dus
2√2 : 3√2 = 21/2 : 21/3 = 21/2 − 1/3 = 21/6
Ik los nu wortels op dmv priemgetallen en dat gaat een stuk beter en ik begrijp het ook veel beter. Eerst ging ik trial and error uitoefenen op de wortels.. om zodoende op een getal uit te komen dat vereenvoudigbaar is etc.. Duurde veelste lang en was ook maar 70% kans dat het goed uitkwam.
Nog éénquote:
[..]
Vierkantswortels komen zo vaak voor dat men de 2 dan meestal weglaat, dus 2√9 is hetzelfde als √9. En je weet toch dat 3 = √9 en ook dat voor a,b > 0 geldt
√a / √b = √(a/b)
Dus hebben we
3 / √3 = √9 / √3 = √3
Andere manier: vermenigvuldig teller en noemer van 3 / √ 3 met √3, dan krijg je
3 / √3 = 3√3 / 3 = √3
7 / 5√7
Ik gebruikte de priemgetallen methode en dus:
5√7 * 7^4 (om zodoende een 5e macht ervan te maken) levert dus op 5√2401 en dat is gewoon 7
en dan de teller:
7 = 5√16807
Aangzien ook de noemer weg is gewerkt dmv 7^4 via de priemgetallen methode, dus ook de teller met 7^4 vermenigvuldigen dus:
5√16807 * 7^4
En dus
5√40353607 / 7
Wat doe ik fout?
Je wil hier kennelijk 5√7 vermenigvuldigen met 5√(74) om 5√(75) = 7 te krijgen in de noemer, maar dan moet je de teller ook vermenigvuldigen met 5√(74).quote:
[..]
Nog één
7 / 5√7
Ik gebruikte de priemgetallen methode en dus:
5√7 * 7^4 (om zodoende een 5e macht ervan te maken) levert dus op 5√2401 en dat is gewoon 7
Nee, zo werkt dat niet, omdat je iets anders doet dan je beweert. Je hebt de noemer niet vermenigvuldigd met 74 en dus mag je de teller ook niet vermenigvuldigen met 74. Je hebt de noemer immers vermenigvuldigd met 5√(74) en dus moet je nu de teller ook vermenigvuldigen met 5√(74). En dan krijg je voor de tellerquote:en dan de teller:
7 = 5√16807
Ja, maar je moet hier niet met van die grote getallen gaan rekenen. Je kunt wel zeggen dat
7 = 5√(75)
Aangzien ook de noemer weg is gewerkt dmv 7^4 via de priemgetallen methode, dus ook de teller met 7^4 vermenigvuldigen dus:
5√(75) · 5√(74) = 5√(79)
En de breuk wordt dan
5√(79−5) = 5√(74)
Maar denk je nu echt dat dit handig is? Wat zou je denken van
7 / 5√7 = 7 / 71/5 = 74/5 = 5√(74) = 5√2401
?
[ Bericht 0% gewijzigd door Riparius op 06-06-2014 22:44:55 ]
Hoe verandert 7 / 71/5 opeens in 74/5 ?quote:
[..]
Je wil hier kennelijk 5√7 vermenigvuldigen met 5√(74) om 5√(75) = 7 te krijgen in de noemer, maar dan moet je de teller ook vermenigvuldigen met 5√(74).
[..]
Nee, zo werkt dat niet, omdat je iets anders doet dan je beweert. Je hebt de noemer niet vermenigvuldigd met 74 en dus mag je de teller ook niet vermenigvuldigen met 74. Je hebt de noemer immers vermenigvuldigd met 5√(74) en dus moet je nu de teller ook vermenigvuldigen met 5√(74). En dan krijg je voor de teller
5√(75) · 5√(74) = 5√(79)
En de breuk wordt dan
5√(79−5) = 5√(74)
Maar denk je nu echt dat dit handig is? Wat zou je denken van
7 / 5√7 = 7 / 71/5 = 74/5 = 5√(74) = 5√2401
?
Ik heb dit keer dit gedaan:quote:
[..]
Je wil hier kennelijk 5√7 vermenigvuldigen met 5√(74) om 5√(75) = 7 te krijgen in de noemer, maar dan moet je de teller ook vermenigvuldigen met 5√(74).
[..]
Nee, zo werkt dat niet, omdat je iets anders doet dan je beweert. Je hebt de noemer niet vermenigvuldigd met 74 en dus mag je de teller ook niet vermenigvuldigen met 74. Je hebt de noemer immers vermenigvuldigd met 5√(74) en dus moet je nu de teller ook vermenigvuldigen met 5√(74). En dan krijg je voor de teller
5√(75) · 5√(74) = 5√(79)
En de breuk wordt dan
5√(79−5) = 5√(74)
Maar denk je nu echt dat dit handig is? Wat zou je denken van
7 / 5√7 = 7 / 71/5 = 74/5 = 5√(74) = 5√2401
?
5 √(7^5 * 7^4) / 5 √(7^1 * 7^4)
= 7 5√(7^4) / 7
En dus 5√(7^4) en dus 74/5
Welke rekenregel voor machten ken je met betrekking tot delingen?quote:
[..]
Hoe verandert 7 / 71/5 opeens in 74/5 ?
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Leer de regels nu eens goed en pas ze systematisch toe...
Weer de bekende rekenregelquote:
[..]
Hoe verandert 7 / 71/5 opeens in 74/5 ?
ap : aq = ap−q
en aangezien 7 = 71 krijg je dan
7 / 71/5 = 71 : 71/5 = 71−1/5 = 74/5
Omdat je de vraag verkeerd interpreteert of overschrijft. Er staat nu ergens a-2. Dat is wiskundige onzin.quote:
((a-²)³(2a³)²)²
Ik kom uit op -a12 * 16a12
Dus -16a24
Antwoordenboek zegt 16a i.p.v -16 ?!
Ik weet niet wat de goede formulering van de vraag wel is, maar bedenk je dit:
(-a)2 = -a*-a =a2, maar -(a2) = -a2. Of een getal eerst gekwadrateerd wordt en dan negatief wordt of andersom is dus essentieel.
Oeps er moest -a^2 staan.. voor de rest staat het er zo.quote:
[..]
Omdat je de vraag verkeerd interpreteert of overschrijft. Er staat nu ergens a-2. Dat is wiskundige onzin.
Ik weet niet wat de goede formulering van de vraag wel is, maar bedenk je dit:
(-a)2 = -a*-a =a2, maar -(a2) = -a2. Of een getal eerst gekwadrateerd wordt en dan negatief wordt of andersom is dus essentieel.
Dan heeft het precies met mijn opmerking te maken. Heb je die gelezen?quote:Op vrijdag 6 juni 2014 23:38 schreef Super-B het volgende:
[..]
Oeps er moest -a^2 staan.. voor de rest staat het er zo.
((−a2)3(2a3)2)2 = (−a6·22·a6)2 = (−4a12)2 = (−4)2(a12)2 = 16a24quote:
[..]
Oeps er moest -a^2 staan.. voor de rest staat het er zo.
Je had natuurlijk direct moeten zien dat er niet iets negatiefs uit kon komen, aangezien de uitdrukking die je moest herleiden een kwadraat is, namelijk het kwadraat van (−a2)3(2a3)2.
Ik heb de uitslag van de wiskunde deficiëntie toets ontvangen via de post. Ik heb een 7,0 behaald! 
[ Bericht 37% gewijzigd door Super-B op 07-06-2014 16:16:58 ]
[ Bericht 37% gewijzigd door Super-B op 07-06-2014 16:16:58 ]
Gefeliciteerdquote:
Ik heb de uitslag van de wiskunde deficiëntie toets ontvangen via de post. Ik heb een 7,0 behaald!
Thanks!quote:
Ik was nog hartstikke onzeker erover toen de toets voorbij was. Want de stof was vrijwel nieuw voor mij. Nja diepgaander, zal ik het zo stellen. Op de havo en op het hbo stelde wiskunde niks voor.
Grappige is dat ik al was begonnen met het leren voor de herkansing. Gelukkig heb ik het voor ''niets'' geleerd. Wat een verademing die 7,0. Ben echt blij!
Nu nog het cijfergemiddelde boven de 7,5 houden (nu tussen de 7,5 a 7,7/7,8) en dan kan ik naar mijn gewenste wo-opleiding.
Gefeliciteerd!!!quote:
Gefeliciteerd SuperB! Ik ben ook geslaagd, met een 8,6
Alleen nog mijn cijfergemiddelde. Enige wegversperring op dit moment!
Heb ik mij de hele tijd voor niks druk gemaaktquote:
[..]
Gefeliciteerd!!!
Alleen nog mijn cijfergemiddelde. Enige wegversperring op dit moment!
Achja
Ik was vandaag en gister nog keihard aan het leren voor de herkansing.quote:
[..]
Heb ik mij de hele tijd voor niks druk gemaakt
Achja
Gelukkig heb ik voor niks geleerd. Liever voor niks leren dan daadwerkelijk moeten herkansen.
Alleen nog die cijfergemiddelde en dan is het echt feest!
Ik denk dat mijn motivatie naar een nulpunt was gedaald als ik een onvoldoende hadquote:
[..]
Ik was vandaag en gister nog keihard aan het leren voor de herkansing.
Gelukkig heb ik voor niks geleerd. Liever voor niks leren dan daadwerkelijk moeten herkansen.
Alleen nog die cijfergemiddelde en dan is het echt feest!
Ik zit wel goed met mijn gemiddelde, ik ben dus zo goed als binnen
Wil je nog voor mij bidden?quote:
[..]
Ik denk dat mijn motivatie naar een nulpunt was gedaald als ik een onvoldoende had
Ik zit wel goed met mijn gemiddelde, ik ben dus zo goed als binnen
Hmm, even een vraag. Als je hebt: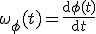 
Waarin φ(t) de hoek is, en dus Omegaphi(t) de hoeksnelheid is, wat voor soort functie is φ(t) dan?
Is sin(x) een voorbeeld van zo'n functie?
Nog een vraag: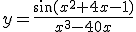
is het mogelijk om van y de afgeleide te bepalen met alleen de kettingregel? Ik had namelijk: 
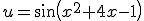en 
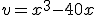waardoor 
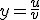en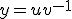 
. 
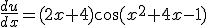met behulp van de kettingregel. En 
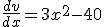. Ik heb geen idee hoe ik nu verder moet.
[ Bericht 12% gewijzigd door netchip op 18-06-2014 21:34:08 ]
Is sin(x) een voorbeeld van zo'n functie?
Nog een vraag:
[ Bericht 12% gewijzigd door netchip op 18-06-2014 21:34:08 ]
hoekpositiequote:
Hmm, even een vraag. Als je hebt:
quote:
Hmm, even een vraag. Als je hebt:
Is sin(x) een voorbeeld van zo'n functie?
Klein detail, sin(x) voldoet niet hieraan, want deze functie is afhankelijk van x en niet van t
Ken je de productregel of de quotiëntregel? Volgens mij is het niet mogelijk om dit met alleen de kettingregel te doen, maar daar denkt Riparius vast anders overquote:Nog een vraag:met behulp van de kettingregel. En
Je maakt hier wel een foutje met de kettingregel. Als je
Dat was een tikfoutjequote:Op woensdag 18 juni 2014 21:21 schreef Alrac4 het volgende:
[..]kan iedere functie zijn die van de tijd afhangt. In veel situaties is dit een periodieke functie, dus dan kom je vaak bij een sinus of cosinus uit, maar dat hoeft zeker niet!
Klein detail, sin(x) voldoet niet hieraan, want deze functie is afhankelijk van x en niet van t
[..]
Ken je de productregel of de quotiëntregel? Volgens mij is het niet mogelijk om dit met alleen de kettingregel te doen, maar daar denkt Riparius vast anders over
Je maakt hier wel een foutje met de kettingregel. Als jeberekent, moet je ook de afgeleide van de sinus meenemen. Snap je?
Ik heb al een tijdje niet meer gedifferentieerd, ik was de hele productregel vergeten 
Nu kan ik hem wel oplossen
Is sin(t) dan wel goed?
Je was kennelijk niet alleen de productregel maar ook de quotiëntregel vergeten. Wonderlijk dat je je dan de kettingregel nog wel kon herinneren. Er is nochtans een eenvoudig ezelsbruggetje om de zowel de productregel als de quotiëntregel af te leiden uit de kettingregel. Ga uit van de bekende rekenregelquote:
[..]
Ik heb al een tijdje niet meer gedifferentieerd, ik was de hele productregel vergeten
ln(uv) = ln(u) + ln(v)
en veronderstel dat u en v differentieerbare functies zijn van eenzelfde variabele. Beide leden differentiëren met behulp van de kettingregel geeft, aangenomen dat u en v alleen positieve waarden aannemen
(uv)'/uv = u'/u + v'/v
en beide leden vermenigvuldigen met uv geeft dan
(uv)' = u'v + uv'
waamee je de productregel hebt gevonden. Geheel analoog kun je de quotiëntregel afleiden door uit te gaan van de rekenregel
ln(u/v) = ln(u) − ln(v)
en beide leden te differentiëren met behulp van de kettingregel, zodat je krijgt
(u/v)'/(u/v) = u'/u − v'/v
Beide leden vermenigvuldigen met u/v geeft dan
(u/v)'= u'/v − uv'/v²
oftewel
(u/v)' = (u'v − uv')/v²
waarmee je de quotiëntregel hebt gevonden. Uiteraard gelden de product- en quotiëntregel eveneens als u en of v niet-positieve waarden aannemen, behalve dat v niet nul mag zijn in het quotiënt u/v aangezien het quotiënt dan geen betekenis heeft.
Inderdaad. Het zal je na lezing van het bovenstaande duidelijk zijn dat het in principe mogelijk is het gebruik van de product- en quotiëntregel te vermijden door gebruik te maken van logaritmisch differentiëren, maar ik raad dit niet aan, en zeker niet aan iemand die de kettingregel niet foutloos kan toepassen.quote:
Ken je de productregel of de quotiëntregel? Volgens mij is het niet mogelijk om dit met alleen de kettingregel te doen, maar daar denkt Riparius vast anders over
Hallo Allemaal,
Ik zit echt met een probleempje
Voor school ben ik al zo ontzettend lang bezig met het analyseren van kwantitatieve gegevens uit Google Analytics. Mijn eindrapport moet minimaal 3 verschillende beschrijvende Statistische methodes en minimaal 2 verschillende verklarende statistische methodes bevatten.
Nu was de ondersteuning in dit cijfermatig gebeuren vanuit de opleiding BAR-slecht. Ik heb meerdere malen tijdens een vragen tienminuutje geprobeerd wijzer te worden, maar in deze tien minuten werd ik niet wijzer, maar juist meer verward. Volgens mij zijn hier mensen die echt verstand hebben van correlaties, regressies en dergelijke. Kan iemand mij op weg helpen met eventueel een voorbeeld?
PS. we worden geadviseerd om met Excel te werken.
Ik zit echt met een probleempje
Voor school ben ik al zo ontzettend lang bezig met het analyseren van kwantitatieve gegevens uit Google Analytics. Mijn eindrapport moet minimaal 3 verschillende beschrijvende Statistische methodes en minimaal 2 verschillende verklarende statistische methodes bevatten.Nu was de ondersteuning in dit cijfermatig gebeuren vanuit de opleiding BAR-slecht. Ik heb meerdere malen tijdens een vragen tienminuutje geprobeerd wijzer te worden, maar in deze tien minuten werd ik niet wijzer, maar juist meer verward. Volgens mij zijn hier mensen die echt verstand hebben van correlaties, regressies en dergelijke. Kan iemand mij op weg helpen met eventueel een voorbeeld?
PS. we worden geadviseerd om met Excel te werken.
Nobody exists on purpose. Nobody belongs anywhere. We're all going to die. Come watch TV.
Ik ben momenteel een keuze-onderwerp aan het voorbereiden van het mondeling examen VWO WisB dat halverwege volgende maand plaatsvind. Het gekozen onderwerp is voortgezette integraalrekening. Het gaat aardig, maar ik betrap mezelf erop dat ik werk met trucjes: ik pas de stappen toe, maar ik begrijp de onderliggende gedachte niet echt. Het begint eigenlijk al bij de volgende (basis-)notatie:
df(x) = f'(x) * dx
df(x) staat voor de afgeleide van f(x), nietwaar? Maar dan zou df(x) = f'(x) toch waar zijn? Waarom staat dx er dan achter? Want dx is toch niets anders dan de afgeleide van x? Of is dit net als bij kettingregel met bijvoorbeeld:
d(x2 + 5)3 = d(u3) = 3u2 * u' = 3(x2 + 5)2 * 2x
Voor de duidelijkheid: ik ben dus wat in de war over de betekenis en toepassing van dx. Bij voorbaat dank
df(x) = f'(x) * dx
df(x) staat voor de afgeleide van f(x), nietwaar? Maar dan zou df(x) = f'(x) toch waar zijn? Waarom staat dx er dan achter? Want dx is toch niets anders dan de afgeleide van x? Of is dit net als bij kettingregel met bijvoorbeeld:
d(x2 + 5)3 = d(u3) = 3u2 * u' = 3(x2 + 5)2 * 2x
Voor de duidelijkheid: ik ben dus wat in de war over de betekenis en toepassing van dx. Bij voorbaat dank
Nee, dy/dx = y'
En omdat vaak geldt y = f(x) geldt dus
d(f(x))/dx = f'(x)
En dus
d(f(x)) = f'(x)dx
Nu staat d(f(x))/dx voor de richtingsafgeleide van f naar de variabele x. Maw je differentieert naar x.
Stel dat je een functie van 2 variabelen hebt, dus g(x,y). Dan dg/dy is de partiële afgeleide van g naar y en dg/dx kun je dan vast wel raden.
[ Bericht 48% gewijzigd door #ANONIEM op 20-06-2014 14:14:12 ]
En omdat vaak geldt y = f(x) geldt dus
d(f(x))/dx = f'(x)
En dus
d(f(x)) = f'(x)dx
Nu staat d(f(x))/dx voor de richtingsafgeleide van f naar de variabele x. Maw je differentieert naar x.
Stel dat je een functie van 2 variabelen hebt, dus g(x,y). Dan dg/dy is de partiële afgeleide van g naar y en dg/dx kun je dan vast wel raden.
[ Bericht 48% gewijzigd door #ANONIEM op 20-06-2014 14:14:12 ]
De uitdrukking df geeft een zogenoemde differentiaalvorm weer. Differentiaalvormen zijn in het algemeen sommen van uitdrukkingen fdg, waarbij f en g functies zijn:quote:
Ik ben momenteel een keuze-onderwerp aan het voorbereiden van het mondeling examen VWO WisB dat halverwege volgende maand plaatsvind. Het gekozen onderwerp is voortgezette integraalrekening. Het gaat aardig, maar ik betrap mezelf erop dat ik werk met trucjes: ik pas de stappen toe, maar ik begrijp de onderliggende gedachte niet echt. Het begint eigenlijk al bij de volgende (basis-)notatie:
df(x) = f'(x) * dx
df(x) staat voor de afgeleide van f(x), nietwaar? Maar dan zou df(x) = f'(x) toch waar zijn? Waarom staat dx er dan achter? Want dx is toch niets anders dan de afgeleide van x? Of is dit net als bij kettingregel met bijvoorbeeld:
d(x2 + 5)3 = d(u3) = 3u2 * u' = 3(x2 + 5)2 * 2x
Voor de duidelijkheid: ik ben dus wat in de war over de betekenis en toepassing van dx. Bij voorbaat dank
Er gelden allerlei rekenregels voor die differentiaalvormen:
Verder geldt ook voor een functie f(x):
Maar de variabele x kun je gewoon als functie interpreteren (dx is niet wezenlijk anders dan df), dus je krijgt hieruit bijvoorbeeld de kettingregel:
Goed om te horen. Op Wikipedia staat ook een heel stuk over differentiaalvormen, waarin ook meer algemene ruimten met meerdere dimensies behandeld worden (mijn post beperkt zich slechts tot differentiaalvormen op een rechte lijn).quote:
Amoeba en thabit, bedankt! Het is nu wél duidelijk
http://en.wikipedia.org/wiki/Differential_form
Dat moet je zo niet opschrijven. De kettingregel luidt in de notatie van Leibnizquote:
d(x2 + 5)3 = d(u3) = 3u2 * u' = 3(x2 + 5)2 * 2x
Voor de duidelijkheid: ik ben dus wat in de war over de betekenis en toepassing van dx. Bij voorbaat dank
dy/dx = dy/du · du/dx
Is nu u = x2 + 5 en y = u3 dan is y = (x2 + 5)3 en dan krijg je dus
d((x2 + 5)3)/dx = d((x2 + 5)3)/d(x2 + 5) · d(x2 + 5)/dx = 3·(x2 + 5)2·2x
Lees dit eens goed door, wellicht begint het dan te dagen.
Ik moet ook dat mondeling gedoe doen. Alleen weet ik niet waar ik me op moet voorbereiden. Heb jij mischien nuttige informatie hierover?quote:Ik ben momenteel een keuze-onderwerp aan het voorbereiden van het mondeling examen VWO WisB dat halverwege volgende maand plaatsvind
hallo
Hoe herken je gemakkelijk welk integraalformule je moet toepassen? Ik raak vaak in de war tussen de afgeleide
integraal f ' (x)*g(x)dx = f(x)*g(x) - integral f(x)* g ' (x) dx
of
integraal f(x)*g ' (x)dx = f(x)*g(x) - integral f ' (x)*g(x) dx
integraal f ' (x)*g(x)dx = f(x)*g(x) - integral f(x)* g ' (x) dx
of
integraal f(x)*g ' (x)dx = f(x)*g(x) - integral f ' (x)*g(x) dx
Geen ervaring met Google Analytics data, wel bijna in het bezit van m'n bachelor diploma Econometrie, dus wieweet?quote:
Hallo Allemaal,
Ik zit echt met een probleempje
Nu was de ondersteuning in dit cijfermatig gebeuren vanuit de opleiding BAR-slecht. Ik heb meerdere malen tijdens een vragen tienminuutje geprobeerd wijzer te worden, maar in deze tien minuten werd ik niet wijzer, maar juist meer verward. Volgens mij zijn hier mensen die echt verstand hebben van correlaties, regressies en dergelijke. Kan iemand mij op weg helpen met eventueel een voorbeeld?
PS. we worden geadviseerd om met Excel te werken.
"Fear is going to be a player in your life, but you get to decide how much."
"You can fail at what you don't want, so you might as well take a chance on doing what you love."
"You can fail at what you don't want, so you might as well take a chance on doing what you love."
Bedankt nog voor de reactie, maar het is nu te laat. De deadline was helaas gisteren, maar ik hoop toch op een voldoende...quote:
[..]
Geen ervaring met Google Analytics data, wel bijna in het bezit van m'n bachelor diploma Econometrie, dus wieweet?
Nobody exists on purpose. Nobody belongs anywhere. We're all going to die. Come watch TV.
f(x)= sin(x2 + x)
Ik weet dat f'(x) = (2x + 1) cos(x2 + x)
Maar ik snap niet echt hoe ik tot de uitwerking kom. Ik dacht zelf het volgende:
f'(x) = (f(x+dx) - f(x))/dx
Maar dan loop ik vast wanneer ik de limiet van dx --> 0 neem...
Ik kom uit op
f'(x)= cos(x2+x) (limdx-->0) (sin(dx2+dx)/dx - sin(x2 + x)(limdx-->0 (1-cos(dx2+dx))/dx
Maar ik snap nu niet hoe ik verder moet en/of ik wel de goede kant op ga. Kan iemand hier mij een duwtje in de goede richting geven?overigens excuses voor het niet gebruiken van Latex
Ik weet dat f'(x) = (2x + 1) cos(x2 + x)
Maar ik snap niet echt hoe ik tot de uitwerking kom. Ik dacht zelf het volgende:
f'(x) = (f(x+dx) - f(x))/dx
Maar dan loop ik vast wanneer ik de limiet van dx --> 0 neem...
Ik kom uit op
f'(x)= cos(x2+x) (limdx-->0) (sin(dx2+dx)/dx - sin(x2 + x)(limdx-->0 (1-cos(dx2+dx))/dx
Maar ik snap nu niet hoe ik verder moet en/of ik wel de goede kant op ga. Kan iemand hier mij een duwtje in de goede richting geven?overigens excuses voor het niet gebruiken van Latex
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |