[Bèta wiskunde] Huiswerk- en vragentopic

Index

» school, studie en onderwijs

actieve topics nieuwe topics
abonnement Unibet Coolblue Bitvavo
pi_139828804
quote:
1s.gif Op zondag 11 mei 2014 16:09 schreef Super-B het volgende:

[..]

Differentiëren kan ik, op de quotiëntregel na.
Snap je dat

\displaystyle \lim_{x \to 0} \frac{e^{x} - 1}{x}

De afgeleide van ex is in het punt x = 0 en dus gelijk aan e0 = 1 ?
pi_139828805
quote:
0s.gif Op zondag 11 mei 2014 13:53 schreef Anoonumos het volgende:
\displaystyle \lim_{x \to 0} \frac{e^{x} - 1}{x} = e^0 = 1
Want die limiet is de afgeleide van ex in x = 0, en de afgeleide van ex is ex.

Daaruit volgt voor elke b:

\displaystyle \lim_{x \to 0} \frac{e^{b x} - 1}{x} = \lim_{x \to 0} \ b \cdot \frac{e^{b x} - 1}{bx} = b \cdot e^0 = b

En dus voor elke a:

\displaystyle \lim_{x \to 0} \frac{a^x - 1}{x} = \lim_{x \to 0} \frac{e^{x \ln a}- 1}{x} = \ln a
Ik snap niet waar de b * vandaan komt en de bx?
pi_139828815
quote:
0s.gif Op zondag 11 mei 2014 16:11 schreef Anoonumos het volgende:

[..]

Snap je dat

\displaystyle \lim_{x \to 0} \frac{e^{x} - 1}{x}

De afgeleide van ex is in het punt x = 0 en dus gelijk aan e0 = 1 ?
Dat begrijp ik. :)
  zondag 11 mei 2014 @ 16:11:48 #154
383325 nodig
ZOEEEEEFF
pi_139828825
quote:
12s.gif Op zondag 11 mei 2014 16:10 schreef Viezze het volgende:

[..]

Deze kroon ik tot de rekenregel van de dag
SPOILER
Om spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
Op maandag 1 juli 2013 18:51 schreef Spatieloos het volgende:
http://vocaroo.com/i/s0UHSJjg0hd5 :@
  zondag 11 mei 2014 @ 16:14:11 #155
383325 nodig
ZOEEEEEFF
pi_139828899
quote:
1s.gif Op zondag 11 mei 2014 16:09 schreef Super-B het volgende:

[..]

Differentiëren kan ik, op de quotiëntregel na.
Die is niet zo heel moeilijk, vind ik.
Op maandag 1 juli 2013 18:51 schreef Spatieloos het volgende:
http://vocaroo.com/i/s0UHSJjg0hd5 :@
pi_139828976
quote:
1s.gif Op zondag 11 mei 2014 16:11 schreef Super-B het volgende:

[..]

Ik snap niet waar de b * vandaan komt en de bx?
\lim_{x \to 0} \frac{e^{bx} - 1}{x}

Vermenigvuldig teller en noemer met b

\lim_{x \to 0} b \cdot \frac{e^{bx} - 1}{bx}

Maar dit is hetzelfde als

b \cdot \lim_{x \to 0} \frac{e^{bx} - 1}{bx} = b \cdot \lim_{bx \to 0} \frac{e^{bx} - 1}{bx}

En die limiet is ook weer de afgeleide van ex in het punt x = 0 want je kan schrijven y = bx en dan wordt het

\lim_{bx \to 0} \frac{e^{bx} - 1}{bx} = \lim_{y \to 0} \frac{e^{y} - 1}{y} = 1

De conclusie is dus

\lim_{x \to 0} \frac{e^{bx} - 1}{x} = b \cdot 1 = b
pi_139829133
quote:
0s.gif Op zondag 11 mei 2014 16:16 schreef Anoonumos het volgende:

[..]

\lim_{x \to 0} \frac{e^{bx} - 1}{x}

Vermenigvuldig teller en noemer met b

\lim_{x \to 0} b \cdot \frac{e^{bx} - 1}{bx}

Maar dit is hetzelfde als

b \cdot \lim_{x \to 0} \frac{e^{bx} - 1}{bx} = b \cdot \lim_{bx \to 0} \frac{e^{bx} - 1}{bx}

En die limiet is ook weer de afgeleide van ex in het punt x = 0 want je kan schrijven y = bx en dan wordt het

\lim_{bx \to 0} \frac{e^{bx} - 1}{bx} = \lim_{y \to 0} \frac{e^{y} - 1}{y} = 1

De conclusie is dus

\lim_{x \to 0} \frac{e^{bx} - 1}{x} = b \cdot 1 = b
Hoe kom je tot de conclusie b * 1 en vervolgens dat het antwoord b is? Ik zie hem niet. Evenals de functie met de y waaruit 1 volgt, waaraan zie je dat?
pi_139829197
quote:
0s.gif Op zondag 11 mei 2014 16:09 schreef Alrac4 het volgende:

[..]

Het eerste deel van je antwoord is goed, dus dat stuk neem ik niet mee. Dan kun je jouw antwoord omschrijven:

\frac{1}{2}*(x+1)^{-1/2}*ln(x) = \frac{1}{2}*\frac{1}{(x+1)^{1/2}}*ln(x) = \frac{1}{2}*\frac{1}{\sqrt{x+1}}*ln(x) = \frac{ln(x)}{2\sqrt{x+1}}
Toppie. Wat doe ik aan deze fout?

Ln x * x^(1/3)

1/x * x^(1/3) + ln x * 1/3x^(-2/3)

1/3 + ln 1/3x^(1/3)

echter hoort die 1/3x gewoon x te zijn, maar geen idee waarom.
pi_139829383
quote:
1s.gif Op zondag 11 mei 2014 16:21 schreef Super-B het volgende:

[..]

Hoe kom je tot de conclusie b * 1 en vervolgens dat het antwoord b is? Ik zie hem niet. Evenals de functie met de y waaruit 1 volgt, waaraan zie je dat?
\displaystyle \lim_{x \to 0} \frac{e^{x} - 1}{x} = e^0= 1
Omdat het de afgeleide van ex in het punt x = 0 is.

\displaystyle \lim_{x \to 0} \frac{e^{bx} - 1}{x} = \lim_{x \to 0} b \cdot \frac{e^{bx} - 1}{bx} = b \cdot \lim_{x \to 0} \frac{e^{bx} - 1}{bx} = b \cdot \lim_{bx \to 0} \frac{e^{bx} - 1}{bx} = b \cdot \lim_{y \to 0} \frac{e^{y} - 1}{y} = b \cdot 1 = b

Die limiet met y volgt dus uit die limiet bovenaan deze post (of je nou x of y gebruikt maakt niks uit)
En ik gebruik dat x -> 0 hetzelfde is als bx -> 0 omdat b toch een constante is.
Goed dat je het probeert te begrijpen maar het is vrij lastig en je hoeft het niet zelf te kunnen op je toets.
Ik denk niet dat ik dit geleerd heb op het vwo.
pi_139829761
quote:
0s.gif Op zondag 11 mei 2014 16:29 schreef Anoonumos het volgende:

[..]

\displaystyle \lim_{x \to 0} \frac{e^{x} - 1}{x} = e^0= 1
Omdat het de afgeleide van ex in het punt x = 0 is.

\displaystyle \lim_{x \to 0} \frac{e^{bx} - 1}{x} = \lim_{x \to 0} b \cdot \frac{e^{bx} - 1}{bx} = b \cdot \lim_{x \to 0} \frac{e^{bx} - 1}{bx} = b \cdot \lim_{bx \to 0} \frac{e^{bx} - 1}{bx} = b \cdot \lim_{y \to 0} \frac{e^{y} - 1}{y} = b \cdot 1 = b

Die limiet met y volgt dus uit die limiet bovenaan deze post (of je nou x of y gebruikt maakt niks uit)
En ik gebruik dat x -> 0 hetzelfde is als bx -> 0 omdat b toch een constante is.
Goed dat je het probeert te begrijpen maar het is vrij lastig en je hoeft het niet zelf te kunnen op je toets.
Ik denk niet dat ik dit geleerd heb op het vwo.
Oh oke gelukkig. Nee maar ik snap niet hoe je kan zien dat het uiteindelijk b * 1 is?
  zondag 11 mei 2014 @ 16:40:38 #161
383325 nodig
ZOEEEEEFF
pi_139829882
Oké,
Bepaal de tweede afgeleide van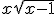 x\sqrt{x-1}

Dus ik kom bij de 1e afgeleide tot:
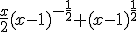
\frac{x}{2}(x-1)^{-\frac{1}{2}}+(x-1)^{\frac{1}{2}}

Maar nu moet ik naar de tweede afgeleide:
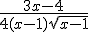
\frac{3x-4}{4(x-1)\sqrt{x-1}}

Hoe doe ik dit?
Op maandag 1 juli 2013 18:51 schreef Spatieloos het volgende:
http://vocaroo.com/i/s0UHSJjg0hd5 :@
pi_139829893
quote:
1s.gif Op zondag 11 mei 2014 16:38 schreef Super-B het volgende:

[..]

Oh oke gelukkig. Nee maar ik snap niet hoe je kan zien dat het uiteindelijk b * 1 is?
\displaystyle \lim_{y \to 0} \frac{e^{y} - 1}{y} = \lim_{x \to 0} \frac{e^{x} - 1}{x} = e^0= 1

(Met die eerste gelijkheid bedoel ik dat het niet uitmaakt welke variabele je gebruikt)
En dus

b \cdot \displaystyle \lim_{y \to 0} \frac{e^{y} - 1}{y} = b \cdot 1 = b
pi_139829923
Ln x^(1/2) * (1-x^2)

ln x(1-x^2) / 2Wx - ln-2x^(3/2) + 2x^2

ik doe wat fout aan de rechterkant...

Ik deed aan de rechterkant dit:

Ln * x^(1/2) * (1-x^2) * -2x
Ln * x^(1/2) * -2x + 2x^2

zo kom ik aan de rechterkant.
pi_139829976
quote:
1s.gif Op zondag 11 mei 2014 16:23 schreef RustCohle het volgende:

[..]

Toppie. Wat doe ik aan deze fout?

Ln x * x^(1/3)

1/x * x^(1/3) + ln x * 1/3x^(-2/3)

1/3 + ln 1/3x^(1/3)

echter hoort die 1/3x gewoon x te zijn, maar geen idee waarom.
Ik begrijp niet helemaal wat je doet tussen de tweede en derde stap. Probeer dit eens iets beter uit te schrijven.

Verder, maak in je posts duidelijk wanneer je een afgeleide neemt en wanneer je je functie omschrijft dus:
f(x) = ln(x)+x^2
f '(x) = 1/x + 2x

En niet:
ln(x)+x^2
1/x + 2x
pi_139829993
quote:
0s.gif Op zondag 11 mei 2014 16:40 schreef Anoonumos het volgende:

[..]

\displaystyle \lim_{y \to 0} \frac{e^{y} - 1}{y} = \lim_{x \to 0} \frac{e^{x} - 1}{x} = e^0= 1

(Met die eerste gelijkheid bedoel ik dat het niet uitmaakt welke variabele je gebruikt)
En dus

b \cdot \displaystyle \lim_{y \to 0} \frac{e^{y} - 1}{y} = b \cdot 1 = b
Ik zie het licht bij het eindantwoord gewoon niet. Hoe kom je aan e^0 en b = 1 ? Ik kan dat gewoon niet zien. De rest is mij wel geheel duidelijk, evenals het variabele dat kan veranderen.
pi_139830076
quote:
0s.gif Op zondag 11 mei 2014 16:40 schreef nodig het volgende:
Oké,
Bepaal de tweede afgeleide van x\sqrt{x-1}

Dus ik kom bij de 1e afgeleide tot:
\frac{x}{2}(x-1)^{-\frac{1}{2}}+(x-1)^{\frac{1}{2}}

Maar nu moet ik naar de tweede afgeleide:
\frac{3x-4}{4(x-1)\sqrt{x-1}}

Hoe doe ik dit?
(x-1)^{\frac{3}{2}} = (x-1)^{\frac{1}{2}} \cdot (x-1) = \sqrt{x-1} (x-1)
Helpt dit?
pi_139830250
quote:
1s.gif Op zondag 11 mei 2014 16:43 schreef Super-B het volgende:

[..]

Ik zie het licht bij het eindantwoord gewoon niet. Hoe kom je aan e^0 en b = 1 ? Ik kan dat gewoon niet zien. De rest is mij wel geheel duidelijk, evenals het variabele dat kan veranderen.
Niet b = 1 maar 1 * b = b.

\lim_{x \to 0} \frac{e^{x} - 1}{x} = e^0 = 1

Die limiet is de afgeleide van ex in het punt x = 0. (Definitie van de afgeleide)
De afgeleide van ex is ex.
Dus de afgeleide van ex in het punt x = 0 is e0 en er geldt e0 = 1.
pi_139830306
quote:
0s.gif Op zondag 11 mei 2014 16:43 schreef Alrac4 het volgende:

[..]

Ik begrijp niet helemaal wat je doet tussen de tweede en derde stap. Probeer dit eens iets beter uit te schrijven.

Verder, maak in je posts duidelijk wanneer je een afgeleide neemt en wanneer je je functie omschrijft dus:
f(x) = ln(x)+x^2
f '(x) = 1/x + 2x

En niet:
ln(x)+x^2
1/x + 2x
De functie is -->

x^(1/2) ln (1-x²)

Hiervan moet ik de afgeleide weten en ik herschreef de functie als:

ln x^(1/2) * (1-x²)

Hierop pas ik de productregel toe, dus:

1/x^(1/2) * (1-x²) + ln x^(1/2) * -2x (1-x²)

Dit wordt:

1/x^(1/2) * (1-x²) + ln x^(1/2) * -2x + 2x³)

1-x² / x^(3/2) + ln x^(1/2) * -2x + 2x³)
pi_139830340
quote:
0s.gif Op zondag 11 mei 2014 13:53 schreef Anoonumos het volgende:
\displaystyle \lim_{x \to 0} \frac{e^{x} - 1}{x} = e^0 = 1
Want die limiet is de afgeleide van ex in x = 0, en de afgeleide van ex is ex.
Dat klopt uiteraard, maar om aan te tonen dat f(x) = ex zichzelf als afgeleide heeft wordt meestal gebruik gemaakt van de 'standaardlimiet'

\displaystyle \lim_{h \to 0} \frac{e^{h} - 1}{h} = 1

en dan beland je dus in een cirkelredenatie als je je weer gaat beroepen op de afgeleide van f(x) = ex in het punt x = 0 om deze limiet te rechtvaardigen ...

Je zou dus eerst deze limiet aan moeten tonen zonder gebruik te maken van de afgeleide van f(x) = ex.

quote:
Daaruit volgt voor elke b:

\displaystyle \lim_{x \to 0} \frac{e^{b x} - 1}{x} = \lim_{x \to 0} \ b \cdot \frac{e^{b x} - 1}{bx} = b \cdot e^0 = b

En dus voor elke a:

\displaystyle \lim_{x \to 0} \frac{a^x - 1}{x} = \lim_{x \to 0} \frac{e^{x \ln a}- 1}{x} = \ln a
Wellicht was het verhelderend geweest als je hierbij even had opgemerkt dat eb = a equivalent is met b = ln a.
Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus
  zondag 11 mei 2014 @ 16:55:36 #170
383325 nodig
ZOEEEEEFF
pi_139830493
quote:
0s.gif Op zondag 11 mei 2014 16:45 schreef Anoonumos het volgende:

[..]

(x-1)^{\frac{3}{2}} = (x-1)^{\frac{1}{2}} \cdot (x-1) = \sqrt{x-1} (x-1)
Helpt dit?
Nee. Die -4 in de teller kan ik nog wel beredeneren. Maar waar die 3x vandaan komt en waar het 2e gedeelte gelaten wordt is me een raadsel.
Op maandag 1 juli 2013 18:51 schreef Spatieloos het volgende:
http://vocaroo.com/i/s0UHSJjg0hd5 :@
pi_139830552
quote:
0s.gif Op zondag 11 mei 2014 16:49 schreef Anoonumos het volgende:

[..]

Niet b = 1 maar 1 * b = b.

\lim_{x \to 0} \frac{e^{x} - 1}{x} = e^0 = 1

Die limiet is de afgeleide van ex in het punt x = 0. (Definitie van de afgeleide)
De afgeleide van ex is ex.
Dus de afgeleide van ex in het punt x = 0 is e0 en er geldt e0 = 1.
Oke.. x = 0? Waaraan zie je dat in de functie... Waar ik in de war van raak is dat als de functie geen x had maar -3x dat het dan opeens -3 wordt?!
pi_139830651
quote:
0s.gif Op zondag 11 mei 2014 16:51 schreef Riparius het volgende:

[..]

Dat klopt uiteraard, maar om aan te tonen dat f(x) = ex zichzelf als afgeleide heeft wordt meestal gebruik gemaakt van de 'standaardlimiet'

\displaystyle \lim_{h \to 0} \frac{e^{h} - 1}{h} = 1

en dan beland je dus in een cirkelredenatie als je je weer gaat beroepen op de afgeleide van f(x) = ex in het punt x = 0 om deze limiet te rechtvaardigen ...

Je zou dus eerst deze limiet aan moeten tonen zonder gebruik te maken van de afgeleide van f(x) = ex.

Ja, daar heb je gelijk in.
Ik begrijp het wel dat mensen in de war raken als je op deze manier in een halve pagina het getal e introduceert, zonder docent.
pi_139830792
quote:
0s.gif Op zondag 11 mei 2014 16:51 schreef RustCohle het volgende:

[..]

De functie is -->

x^(1/2) ln (1-x²)

Hiervan moet ik de afgeleide weten en ik herschreef de functie als:

ln x^(1/2) * (1-x²)

Hierop pas ik de productregel toe, dus:

1/x^(1/2) * (1-x²) + ln x^(1/2) * -2x (1-x²)

Dit wordt:

1/x^(1/2) * (1-x²) + ln x^(1/2) * -2x + 2x³)

1-x² / x^(3/2) + ln x^(1/2) * -2x + 2x³)
Dit is hartstikke fout. Ik kan niet meer verder. Kan iemand hem even doen voor me? Helaas heeft het antwoordenboek alleen een antwoord staan en geen uitwerking.
pi_139830808
quote:
0s.gif Op zondag 11 mei 2014 16:51 schreef RustCohle het volgende:

[..]

De functie is -->

x^(1/2) ln (1-x²)

Hiervan moet ik de afgeleide weten en ik herschreef de functie als:

ln x^(1/2) * (1-x²)

Hierop pas ik de productregel toe, dus:

1/x^(1/2) * (1-x²) + ln x^(1/2) * -2x (1-x²)

Dit wordt:

1/x^(1/2) * (1-x²) + ln x^(1/2) * -2x + 2x³)

1-x² / x^(3/2) + ln x^(1/2) * -2x + 2x³)
Volgens mij gaat het helemaal in het begin al fout
x^{1/2}*ln(1-x^2) \ne ln(x^{1/2})*(1-x^2)
pi_139830940
quote:
0s.gif Op zondag 11 mei 2014 17:02 schreef Alrac4 het volgende:

[..]

Volgens mij gaat het helemaal in het begin al fout
x^{1/2}*ln(1-x^2) \ne ln(x^{1/2})*(1-x^2)
Ik dacht dat je dat mocht omdraaien omdat het vermenigvuldiging is en de volgorde niet uitmaakt
pi_139831129
quote:
0s.gif Op zondag 11 mei 2014 17:02 schreef Alrac4 het volgende:

[..]

Volgens mij gaat het helemaal in het begin al fout
x^{1/2}*ln(1-x^2) \ne ln(x^{1/2})*(1-x^2)
Nu kom ik uit op:

1/2x^(-1/2) * ln - lnx² + x^(1/2) * -2x + 2x³
pi_139831293
quote:
0s.gif Op zondag 11 mei 2014 16:55 schreef nodig het volgende:

[..]

Nee. Die -4 in de teller kan ik nog wel beredeneren. Maar waar die 3x vandaan komt en waar het 2e gedeelte gelaten wordt is me een raadsel.
f(x) = \frac{x}{2} (x-1)^{- \frac{1}{2}}

Met productregel

f ' (x) = \frac{1}{2} (x-1)^{-\frac{1}{2}} - \frac{x}{4} (x-1)^{-\frac{3}{2}} = \frac{1}{2 \sqrt{x-1}} - \frac{x}{4(x-1)\sqrt{x-1}}

En

g(x) = (x-1)^{\frac{1}{2}}

Geeft

g ' (x) = \frac{1}{2}(x-1)^{- \frac{1}{2}} = \frac{1}{2 \sqrt{x-1}}

Dus

f ' (x) + g ' (x) = \frac{1}{2 \sqrt{x-1}} - \frac{x}{4(x-1)\sqrt{x-1}} + \frac{1}{2 \sqrt{x-1}} = \frac{1}{ \sqrt{x-1}} - \frac{x}{4(x-1)\sqrt{x-1}} = \frac{4(x-1)}{4(x-1) \sqrt{x-1}} - \frac{x}{4(x-1)\sqrt{x-1}} = \frac{3x-4}{4(x-1) \sqrt{x-1}}

[ Bericht 0% gewijzigd door Anoonumos op 11-05-2014 17:38:07 ]
pi_139831438
quote:
0s.gif Op zondag 11 mei 2014 17:08 schreef RustCohle het volgende:

[..]

Nu kom ik uit op:

1/2x^(-1/2) * ln - lnx² + x^(1/2) * -2x + 2x³
Dit resulteert tot

ln(1-x²) / 2√x - 2x^(3/2) / ..... op dit puntjes weet ik niet wat er moet komen, er blijft wel +2x³ over... maar dat moet daar niet staan, dat weet ik wel.
pi_139831982
quote:
0s.gif Op zondag 11 mei 2014 16:59 schreef Anoonumos het volgende:

[..]

Ja, daar heb je gelijk in.
Ik begrijp het wel dat mensen in de war raken als je op deze manier in een halve pagina het getal e introduceert, zonder docent.
Vroeger werd in het elementair onderwijs vaak eerst de afgeleide van de algemene logaritmische functie f(x) = glog x hehandeld en dan kom je uit bij de limiet van (1 + k)1/k voor k → 0 (zie hier en hier). Dat is een natuurlijker manier om leerlingen het getal e te laten 'ontdekken'. Een andere methode was om de behandeling van e uit te stellen tot de behandeling van de integraalrekening. De zoektocht (samen met de leerlingen) naar de 'ontbrekende' primitieve van x−1 leidde dan tot een functie die alle eigenschappen van een logaritmische functie bleek te hebben en dus ook een logaritmische functie was, maar dan wel één met een bijzonder grondtal.
Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus
  zondag 11 mei 2014 @ 17:34:28 #180
383325 nodig
ZOEEEEEFF
pi_139832473
quote:
0s.gif Op zondag 11 mei 2014 17:12 schreef Anoonumos het volgende:

[..]

f(x) = \frac{x}{2} (x-1)^{- \frac{1}{2}}

Met productregel

f ' (x) = \frac{1}{2} (x-1)^{-\frac{1}{2}} - \frac{x}{4} (x-1)^{-\frac{3}{2}} = \frac{1}{2 \sqrt{x-1}} - \frac{x}{4(x-1)\sqrt{x-1}}

En

g(x) = (x-1)^{-\frac{1}{2}}

Geeft

g ' (x) = \frac{1}{2}(x-1)^{- \frac{1}{2}} = \frac{1}{2 \sqrt{x-1}}

Dus

f ' (x) + g ' (x) = \frac{1}{2 \sqrt{x-1}} - \frac{x}{4(x-1)\sqrt{x-1}} + \frac{1}{2 \sqrt{x-1}} = \frac{1}{ \sqrt{x-1}} - \frac{x}{4(x-1)\sqrt{x-1}} = \frac{4(x-1)}{4(x-1) \sqrt{x-1}} - \frac{x}{4(x-1)\sqrt{x-1}} = \frac{3x-4}{4(x-1) \sqrt{x-1}}
Dankjewel!

Hoezo tel je g'(x) erbij op? Ik dacht dat het antwoord datgene na de productregel al was.
Op maandag 1 juli 2013 18:51 schreef Spatieloos het volgende:
http://vocaroo.com/i/s0UHSJjg0hd5 :@
pi_139832608
quote:
0s.gif Op zondag 11 mei 2014 17:34 schreef nodig het volgende:

[..]

Dankjewel!

Hoezo tel je g(x) erbij op?
Je begon met
x \sqrt{x-1}
De afgeleide daarvan is
f(x) + g(x)
(zoals je zelf had laten zien, ik heb alleen de namen f(x) en g(x) gegeven)

En (f(x) + g(x)) ' = f' ' (x) + g ' (x) rekenregel

Ik had een foutje gemaakt bij het schrijven van g(x). Nu aangepast.
  zondag 11 mei 2014 @ 17:40:27 #182
371309 t4rt4rus
Tartarus
pi_139832749
quote:
1s.gif Op zondag 11 mei 2014 16:09 schreef Super-B het volgende:

[..]

Differentiëren kan ik, op de quotiëntregel na.
Als in het onthouden van dat ding?
Dan los je het gewoon anders op

\frac{f(x)}{g(x)} = f(x) [g(x)]^{-1}
  zondag 11 mei 2014 @ 17:44:51 #183
383325 nodig
ZOEEEEEFF
pi_139832921
quote:
0s.gif Op zondag 11 mei 2014 17:37 schreef Anoonumos het volgende:

[..]

Je begon met
x \sqrt{x-1}
De afgeleide daarvan is
f(x) + g(x)
(zoals je zelf had laten zien, ik heb alleen de namen f(x) en g(x) gegeven)

En (f(x) + g(x)) ' = f' ' (x) + g ' (x) rekenregel

Ik had een foutje gemaakt bij het schrijven van g(x). Nu aangepast.
Oh, ik zie het al, ik was die g(x) even uit het oog verloren :P

En ik maar kijken welke differentieerregel ik over het hoofd zag :P
Thanks trouwens! Zonder jouw hulp was ik er niet uitgekomen :)
Op maandag 1 juli 2013 18:51 schreef Spatieloos het volgende:
http://vocaroo.com/i/s0UHSJjg0hd5 :@
pi_139833815
Kan iemand helpen bij het differentieren van :

√x (^5log x³)

^5 is dus het grondgetal van de log.

Ik had:

1/2x^(-1/2) * ^5log x³ + x^(1/2) * 1 / (x³ ln 5)
pi_139833822
quote:
0s.gif Op zondag 11 mei 2014 17:05 schreef RustCohle het volgende:

[..]

Ik dacht dat je dat mocht omdraaien omdat het vermenigvuldiging is en de volgorde niet uitmaakt
Nee, dat mag in dit geval niet op deze manier. De natuurlijke logaritme is een functie. Dat betekent dat hij werkt op een getal. Het stuk ln(1-x2) hoort bij elkaar en dit mag je alleen als geheel verschuiven. Je kunt dus wel zeggen:
x^{1/2}*ln(1-x^2) = ln(1-x^2)*x^{1/2}

quote:
0s.gif Op zondag 11 mei 2014 17:08 schreef RustCohle het volgende:

[..]

Nu kom ik uit op:

1/2x^(-1/2) * ln - lnx² + x^(1/2) * -2x + 2x³
Volgens mij doe je hier:
ln(1-x2) = ln(1) - ln(x2)
Dit mag niet!
Vergelijk het met kwadrateren, daar geldt ook niet (2+3)2 = 22+32
Als je iets hebt van de vorm ln(a+b) moet je dat gewoon zo laten staan, dit kun je niet verder vereenvoudigen.

Ook in de tweede term gaat iets fout.
Je moet inderdaad x1/2 gewoon laten staan. Maar dit moet je dan vermenigvuldigen met de afgeleide van ln(1-x2).
Wat is deze afgeleide volgens jou?
  zondag 11 mei 2014 @ 18:11:02 #186
371309 t4rt4rus
Tartarus
pi_139833902
quote:
0s.gif Op zondag 11 mei 2014 18:07 schreef RustCohle het volgende:
Kan iemand helpen bij het differentieren van :

√x (^5log x³)

^5 is dus het grondgetal van de log.

Ik had:

1/2x^(-1/2) * ^5log x³ + x^(1/2) * 1 / (x³ ln 5)
Ooit van kettingregel gehoord?
pi_139833923
quote:
0s.gif Op zondag 11 mei 2014 18:08 schreef Alrac4 het volgende:

[..]

Nee, dat mag in dit geval niet op deze manier. De natuurlijke logaritme is een functie. Dat betekent dat hij werkt op een getal. Het stuk ln(1-x2) hoort bij elkaar en dit mag je alleen als geheel verschuiven. Je kunt dus wel zeggen:
x^{1/2}*ln(1-x^2) = ln(1-x^2)*x^{1/2}

[..]

Volgens mij doe je hier:
ln(1-x2) = ln(1) - ln(x2)
Dit mag niet!
Vergelijk het met kwadrateren, daar geldt ook niet (2+3)2 = 22+32
Als je iets hebt van de vorm ln(a+b) moet je dat gewoon zo laten staan, dit kun je niet verder vereenvoudigen.

Ook in de tweede term gaat iets fout.
Je moet inderdaad x1/2 gewoon laten staan. Maar dit moet je dan vermenigvuldigen met de afgeleide van ln(1-x2).
Wat is deze afgeleide volgens jou?
Oh even kijken.. Ik ga hem even opnieuw proberen, dus ik mag met ln niet kwadrateren ofwel de bananenformule toepassen? Gewoon zo laten staan?
pi_139833937
quote:
0s.gif Op zondag 11 mei 2014 18:11 schreef t4rt4rus het volgende:

[..]

Ooit van kettingregel gehoord?
Ja.Ik dacht dat ik de productregel moest toepassen?
  zondag 11 mei 2014 @ 18:12:57 #189
371309 t4rt4rus
Tartarus
pi_139833966
quote:
0s.gif Op zondag 11 mei 2014 18:12 schreef RustCohle het volgende:

[..]

Ja.Ik dacht dat ik de productregel moest toepassen?
Ook, dat heb je dus deels gedaan, nu moet je alleen nog de kettingregel toepassen om het af te maken.
pi_139834011
quote:
0s.gif Op zondag 11 mei 2014 18:12 schreef t4rt4rus het volgende:

[..]

Ook, dat heb je dus deels gedaan, nu moet je alleen nog de kettingregel toepassen om het af te maken.
Ik heb het even opnieuw gedaan en kwam dit keer uit op:

1/2x^(-1/2) * 3 (^5log x) + x^(1/2) * (1 / x ln 5) * 3
pi_139834081
quote:
0s.gif Op zondag 11 mei 2014 18:11 schreef RustCohle het volgende:

[..]

Oh even kijken.. Ik ga hem even opnieuw proberen, dus ik mag met ln niet kwadrateren ofwel de bananenformule toepassen? Gewoon zo laten staan?
Inderdaad, je mag hier niet de haakjes uitwerken. Je moet dit gewoon zo laten staan
  zondag 11 mei 2014 @ 18:17:37 #192
371309 t4rt4rus
Tartarus
pi_139834094
quote:
0s.gif Op zondag 11 mei 2014 18:14 schreef RustCohle het volgende:

[..]

Ik heb het even opnieuw gedaan en kwam dit keer uit op:

1/2x^(-1/2) * 3 (^5log x) + x^(1/2) * (1 / x ln 5) * 3
Schrijf even de stappen op. En echt een keer duidelijk, maar goed dat heb ik je nog niet zien doen..

Wat krijg je als je f(x) ln(g(x)) differentieerd?
pi_139834164
quote:
0s.gif Op zondag 11 mei 2014 18:17 schreef Alrac4 het volgende:

[..]

Inderdaad, je mag hier niet de haakjes uitwerken. Je moet dit gewoon zo laten staan
1/2x^(-1/2) * ln ( 1 - x² )

wordt

1/2x^(-1/2) * ln (1-x²) + x^(1/2) * -2x * (1-x²)


Ik heb nu

(ln (1-x²) / 2x ) - 2x^(3/2) * (1-x²)

Nu weet ik niet wat ik met - 2x^(3/2) * (1-x²) aan moet>?
pi_139834187
quote:
0s.gif Op zondag 11 mei 2014 18:17 schreef t4rt4rus het volgende:

[..]

Schrijf even de stappen op. En echt een keer duidelijk, maar goed dat heb ik je nog niet zien doen..

Wat krijg je als je f(x) ln(g(x)) differentieerd?
Oke ga ik nu even doen.
  zondag 11 mei 2014 @ 18:25:07 #195
371309 t4rt4rus
Tartarus
pi_139834373
quote:
0s.gif Op zondag 11 mei 2014 18:20 schreef RustCohle het volgende:

[..]

Oke ga ik nu even doen.
Oh en niet alleen maar "wordt" en "dus" gebruiken.
Gewoon zeggen wat je ook echt aan het doen bent.
pi_139834463
quote:
0s.gif Op zondag 11 mei 2014 18:25 schreef t4rt4rus het volgende:

[..]

Oh en niet alleen maar "wordt" en "dus" gebruiken.
Gewoon zeggen wat je ook echt aan het doen bent.
√x (^5 log x³)

Herschrijven tot:

x^(1/2) * (^5 log x³)

Productregel toepassen en dus de afgeleide bepalen;

1/2x^(-1/2) * (^5 log x³) + x^(1/2 ) * ( 1 / x³ ln 5 )

Hier zit ik vast.
  zondag 11 mei 2014 @ 18:28:34 #197
371309 t4rt4rus
Tartarus
pi_139834512
quote:
0s.gif Op zondag 11 mei 2014 18:27 schreef RustCohle het volgende:

[..]

√x (^5 log x³)

Herschrijven tot:

x^(1/2) * (^5 log x³)

Productregel toepassen en dus de afgeleide bepalen;

1/2x^(-1/2) * (^5 log x³) + x^(1/2 ) * ( 1 / x³ ln 5 )

Hier zit ik vast.
Ja dat had je net ook al.
Maar hoe heb jij de afgeleide van (^5log x³) berekend?
pi_139834803
quote:
0s.gif Op zondag 11 mei 2014 18:28 schreef t4rt4rus het volgende:

[..]

Ja dat had je net ook al.
Maar hoe heb jij de afgeleide van (^5log x³) berekend?
Standaardfuncties en hun afgeleiden:

^a log x ' = 1 / x ln a

Dus ik dacht

(^5 log x³) ' = 1 / x³ ln 5
  zondag 11 mei 2014 @ 18:37:44 #199
371309 t4rt4rus
Tartarus
pi_139834836
quote:
0s.gif Op zondag 11 mei 2014 18:36 schreef RustCohle het volgende:

[..]

Standaardfuncties en hun afgeleiden:

^a log x ' = 1 / x ln a

Dus ik dacht

(^5 log x³) ' = 1 / x³ ln 5
En wat is de kettingregel?
pi_139835238
quote:
0s.gif Op zondag 11 mei 2014 18:37 schreef t4rt4rus het volgende:

[..]

En wat is de kettingregel?
afgeleide van functie f(x) optellen met de afgeleide van functie g(x)
actieve topics nieuwe topics
abonnement Unibet Coolblue Bitvavo
[Bèta wiskunde] Huiswerk- en vragentopic
Index

» school, studie en onderwijs

Forum Opties
Forumhop:
Hop naar:
(afkorting, bv 'KLB')