SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Ik heb gevonden bij de ongelijkheid x^2 < 2x+8
voor x > -2 en x < 4.
Waarom schrijf je dit als -2 < x < 4 ? Ik snap de logica van die notatie niet.
voor x > -2 en x < 4.
Waarom schrijf je dit als -2 < x < 4 ? Ik snap de logica van die notatie niet.
Je behandelt nu een pseudo-cilindrische projectie, correct? Met een oorsprong in het middelpunt vd aarde, dus gnomonisch?
Ik begrijp wat je bedoelt. Je wilt alle parallellen nog steeds opschalen naar de lengte vd evenaar, dus horizontaal gezien vermenigvuldig je moet sec φ, dus verticaal vermenigvuldig je met cos φ, zodat je de constante behoudt. Inderdaad krijg je dan weer de gegeven aanpak om tot de differentiaalvergelijking te komen, de constante vervalt vanwege je laatste regel. Helder.
Ik ben nu echter bezig met directe projecties, zonder niet-geometrische bewerkingen. Snap je mij?
Wederom bedankt voor je heldere uitleg.
Ik ga hier iets mee doen.
Ik begrijp wat je bedoelt. Je wilt alle parallellen nog steeds opschalen naar de lengte vd evenaar, dus horizontaal gezien vermenigvuldig je moet sec φ, dus verticaal vermenigvuldig je met cos φ, zodat je de constante behoudt. Inderdaad krijg je dan weer de gegeven aanpak om tot de differentiaalvergelijking te komen, de constante vervalt vanwege je laatste regel. Helder.
Ik ben nu echter bezig met directe projecties, zonder niet-geometrische bewerkingen. Snap je mij?
Wederom bedankt voor je heldere uitleg.
Ik ga hier iets mee doen.
Scheelt wat schrijfwerk. Er staat precies hetzelfde hoor.quote:Op maandag 10 december 2012 19:25 schreef rareziekte het volgende:
Ik heb gevonden bij de ongelijkheid x^2 < 2x+8
voor x > -2 en x < 4.
Waarom schrijf je dit als -2 < x < 4 ? Ik snap de logica van die notatie niet.
Ja, dat is een sluitend bewijs voor conformiteit. Inderdaad is de hoek die twee snijdende krommen met elkaar maken niets anders dan de hoek tussen de raaklijnen aan de krommen in het snijpunt. Merk op dat een loxodroom op het boloppervlak zo een logaritmische oftewel een equiangulaire spiraal oplevert in het projectievlak bij een stereografische projectie.quote:Op maandag 10 december 2012 17:57 schreef Amoeba het volgende:
[..]
De methode door te bewijzen (meetkundig) dat de hoek die 2 raaklijnen aan een bol maken equivalent is aan de hoek die de projecties van die lijnen met elkaar maken, is dat ook een sluitend bewijs? Immers, de hoek die 2 krommen maken is gelijk aan de hoek die hun raaklijnen maken.
Als je een analytische functie w = f(z) hebt en een (gladde) kromme z = γ(t) in het complexe vlak dan wordt de richting van de raaklijn aan de kromme in een punt z0 = γ(t0) bepaald door het argument van dz/dt voor t = t0, dus het argument van γ'(t0). En de richting van de raaklijn aan de afbeelding w = f(γ(t)) van de kromme in het w-vlak wordt dan evenzo bepaald door het argument van dw/dt voor t = t0 oftewel het argument van f'(z0)∙γ'(t0) aangezien dw/dt = dw/dz ∙ dz/dt (kettingregel). En aangezien vermenigvuldiging met f'(z0) ≠ 0 een draaistrekking inhoudt (i.e. een schaling met een factor | f'(z0) | en tevens een rotatie equivalent met het argument van f'(z0)) zie je dat een analytische functie w = f(z) een (lokaal) conforme afbeelding geeft van (een deel van) het z-vlak op (een deel van) het w-vlak mits f'(z) ≠ 0.
Als twee krommen elkaar onder een bepaalde hoek snijden in een punt z0 dan snijden hun afbeeldingen in het w-vlak elkaar in het punt w0 = f(z0) onder dezelfde hoek aangezien de rotatie van elk van de raaklijnen gelijk is aan het argument van f'(z0) ≠ 0 zodat hun onderlinge hoek gelijk blijft. Een mooi voorbeeld is de functie f(z) = ez die horizontale rechte lijnen (evenwijdig aan de reële as) afbeeldt als lijnen door de oorsprong in het w-vlak, terwijl verticale rechte lijnen (evenwijdig aan de imaginaire as) worden afgebeeld als cirkels rond de oorsprong. Je ziet dus dat de afbeeldingen van een horizontale en een verticale rechte lijn elkaar inderdaad weer loodrecht snijden, aangezien een rechte lijn door het middelpunt van een cirkel de cirkel loodrecht snijdt.
[ Bericht 0% gewijzigd door Riparius op 10-12-2012 21:09:18 ]
x voldoet tegelijk aan allebei die eisen en ligt tussen die twee waarden, dat is wat de logica achter die notatie is.quote:
Ik heb gevonden bij de ongelijkheid x^2 < 2x+8
voor x > -2 en x < 4.
Waarom schrijf je dit als -2 < x < 4 ? Ik snap de logica van die notatie niet.
Als je het beter wil snappen: teken de x-as als een staaf en kleur de gebieden, waar x is volgens de eisen, in. Het gebied dat je dubbel inkleurt is dan -2 < x < 4.
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Waarom niet -2 > x < 4 ?quote:
[..]
x voldoet tegelijk aan allebei die eisen en ligt tussen die twee waarden, dat is wat de logica achter die notatie is.
Als je het beter wil snappen: teken de x-as als een staaf en kleur de gebieden, waar x is volgens de eisen, in. Het gebied dat je dubbel inkleurt is dan -2 < x < 4.
Je moet -2 < x < 4 lezen als "-2 < x (-2 is kleiner dan x, dus x is groter dan -2) en x < 4 (x is kleiner dan 4)". Voeg die twee samen en je hebt "x tussen -2 en 4". In jouw notatie staat er "-2 > x (dus -2 groter dan x, x kleiner dan -2) en x < 4". Het tweede statement is dan overbodig.quote:
The biggest argument against democracy is a five minute discussion with the average voter.
Oke, thxquote:
[..]
Je moet -2 < x < 4 lezen als "-2 < x (-2 is kleiner dan x, dus x is groter dan -2) en x < 4 (x is kleiner dan 4)". Voeg die twee samen en je hebt "x tussen -2 en 4". In jouw notatie staat er "-2 > x (dus -2 groter dan x, x kleiner dan -2) en x < 4". Het tweede statement is dan overbodig.
Ah, ik snap je probleemquote:
> is een teken dat betekent: is groter dan.
Dus
4 > 3 houdt in: 4 is groter dan.
x > -2 houdt in: x is groter dan -2.
< is een teken dat betekent: is kleiner dan.
Dus
2 < 3 houdt in: 2 is kleiner dan 3.
x < 4 houdt in: x is kleiner dan 4.
-2<x<4 houdt in: x is groter dan -2 en x is kleiner dan 4. Equivalent geformuleerd: x is groter dan -2 en kleiner dan 4.
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Dankjewel. Nu komt betreffende dit onderdeel mijn laatste vraag.quote:
[..]
Ja, dat is een sluitend bewijs voor conformiteit. Inderdaad is de hoek die twee snijdende krommen met elkaar maken niets anders dan de hoek tussen de raaklijnen aan de krommen in het snijpunt. Merk op dat een loxodroom op het boloppervlak zo een logaritmische oftewel een equiangulaire spiraal oplevert in het projectievlak bij een stereografische projectie.
Deze afbeelding:
Heeft dus een paar eigenschappen. De lijnen m en l zijn raaklijnen aan de bol in P. Nu vormt de lijn WV een lijn in het grondvlak (tevens projectievlak en raakvlak aan de as), is punt A de projectie van P (stereografisch (cilindrisch)), en is ON de as van de bol. Goed, nu is mijn vraag:
Je ziet bij R een hoekje staan van 90 graden, waarom is dit zo? Ofwel, waarom snijdt WV NA loodrecht. Dat is het enige stukje wat ik niet volg aan de bewijsvoering. Doordat WV in het raakvlak ligt, en R in de driehoek NPA ligt? *gezien PN feitelijk loodrecht op l en m moet staan, want N ligt op de as van de bol.
Ik begrijp niet precies wat je met deze term bedoelt, ik reageerde op jouw eerdere vraag hierboven waar je naar het Wikipedia artikel over de orthografische oftewel oppervlaktegetrouwe cilinderprojectie van Lambert verwijst. Je hebt natuurlijk ook nog de equidistante cilinderprojectie, maar die is weer niet oppervlaktegetrouw.quote:
Je behandelt nu een pseudo-cilindrische projectie, correct? Met een oorsprong in het middelpunt vd aarde, dus gnomonisch?
Uiteindelijk zijn alle kaartprojecties ook zuiver meetkundig te beschrijven.quote:Ik ben nu echter bezig met directe projecties, zonder niet-geometrische bewerkingen. Snap je mij?
Het raakvlak aan punt P van de bol staat loodrecht op straal MP en het raakvlak aan punt N van de bol (i.e. het projectievlak) staat loodrecht op straal MN. Dus staan zowel zowel het raakvlak aan punt P als het projectievlak loodrecht op het vlak bepaald door de punten M, N en P. En aangezien WR in het projectievlak ligt en RA in het vlak bepaald door de punten M,N,P is dus WR ⟂ RA.quote:Op maandag 10 december 2012 20:24 schreef Amoeba het volgende:
[..]
Dankjewel. Nu komt betreffende dit onderdeel mijn laatste vraag.
Deze afbeelding:
[ afbeelding ]
Heeft dus een paar eigenschappen. De lijnen m en l zijn raaklijnen aan de bol in P. Nu vormt de lijn WV een lijn in het grondvlak (tevens projectievlak en raakvlak aan de as), is punt A de projectie van P (stereografisch (cilindrisch)), en is ON de as van de bol. Goed, nu is mijn vraag:
Je ziet bij R een hoekje staan van 90 graden, waarom is dit zo? Ofwel, waarom snijdt WV NA loodrecht. Dat is het enige stukje wat ik niet volg aan de bewijsvoering.
Pseudo-cilindrisch betekent een niet directe projectie. Dus een Mercatorprojectie, maar geen stereografische cilindrische projectie (van Braun), maar met een schaalafhankelijke correctie.quote:
[..]
Ik begrijp niet precies wat je met deze term bedoelt, ik reageerde op jouw eerdere vraag hierboven waar je naar het Wikipedia artikel over de orthografische oftewel oppervlaktegetrouwe cilinderprojectie van Lambert verwijst. Je hebt natuurlijk ook nog de equidistante cilinderprojectie, maar die is weer niet oppervlaktegetrouw.
Gnomonisch, als je die bedoelt, is dat de oorsprong van de projectie in het midden van de figuur ligt. Dus punt M in mijn figuur, maar gezien de projectie stereografisch is is dus het projectiepunt O.
Eenvoudig eigenlijk. Dank.quote:
[..]
Het raakvlak aan punt P van de bol staat loodrecht op straal MP en het raakvlak aan punt N van de bol (i.e. het projectievlak) staat loodrecht op straal MN. Dus staan zowel zowel het raakvlak aan punt P als het projectievlak loodrecht op het vlak bepaald door de punten M, N en P. En aangezien WR in het projectievlak ligt en RA in het vlak bepaald door de punten M,N,P is dus WR ⟂ RA.
Kan ik morgen weer aan de gang.
[ Bericht 3% gewijzigd door #ANONIEM op 10-12-2012 21:53:40 ]
O zo.quote:
[..]
Pseudo-cilindrisch betekent een niet directe projectie. Dus een Mercatorprojectie, maar geen stereografische cilindrische projectie (van Braun), maar met een schaalafhankelijke correctie.
Ik ben geen cartograaf, maar ik heb inmiddels het Wikipedia artikel gelezen en ik zie wat je bedoelde.quote:Gnomonisch, als je die bedoelt, is dat de oorsprong van de projectie in het midden van de figuur ligt. Dus punt M in mijn figuur, maar gezien de projectie stereografisch is is dus het projectiepunt O.
Ben je al klaar met de complexe getallen omdat je je nu weer in de cartografie stort?quote:[..]
Eenvoudig eigenlijk. Dank.
Kan ik morgen weer aan de gang.
Jazeker, hoofdstuk afgerond met een 9,6 voor het proefwerk. Ik doe mijn profielwerkstuk over de cilindrische projecties, vandaar dat ik het weer opgepakt heb. Wiskunde D houdt nu een hoofdstukje Kansen en Beslissingen in. Hypothesetoetsen en zulk soort zooi. Altijd beter dan Duits, enfin.
En je gaf een flink stuk complexe getallen net.. Het enige wat ik begreep was de projecties van reëele delen en imaginaire delen bij ez. Spijtig.
[ Bericht 22% gewijzigd door #ANONIEM op 10-12-2012 22:17:41 ]
En je gaf een flink stuk complexe getallen net.. Het enige wat ik begreep was de projecties van reëele delen en imaginaire delen bij ez. Spijtig.
[ Bericht 22% gewijzigd door #ANONIEM op 10-12-2012 22:17:41 ]
Denk ik toch anders over. Een goede leesvaardigheid Duits is heel nuttig als je verder wil met wiskunde. Er zijn massa's Duitse boeken, artikelen, dictaten e.d. te vinden over bijna elk denkbaar onderwerp, en daar zitten kwalitatief uitstekende teksten bij.quote:Op maandag 10 december 2012 22:16 schreef Amoeba het volgende:
Jazeker, hoofdstuk afgerond met een 9,6 voor het proefwerk. Ik doe mijn profielwerkstuk over de cilindrische projecties, vandaar dat ik het weer opgepakt heb. Wiskunde D houdt nu een hoofdstukje Kansen en Beslissingen in. Hypothesetoetsen en zulk soort zooi. Altijd beter dan Duits, enfin.
Vreemd, ik dacht dat ik het toch duidelijk had uitgelegd. Een analytische (of : holomorfe) functie geeft een (lokaal) conforme afbeelding. Lees anders nog eens in het boekje van Maor na (hier) hoe hij de Mercatorprojectie in verband brengt met de complexe logaritme.quote:En je gaf een flink stuk complexe getallen net.. Het enige wat ik begreep was de projecties van reële delen en imaginaire delen bij ez. Spijtig.
[ Bericht 1% gewijzigd door Riparius op 10-12-2012 22:58:11 ]
Bijna alle wetenschap gaat toch in het Engels? Volgens mij zijn er wel veel oude werken die alleen in het Duits te lezen zijn, dus voor jou is Duitse kennis onmisbaar. Maar als je moderne onderwerpen bestudeert heb je voor zover ik weet geen Duitse taal nodig.quote:
[..]
Denk ik toch anders over. Een goede leesvaardigheid Duits is heel nuttig als je verder wil met wiskunde. Er zijn massa's Duitse boeken, artikelen, dictaten e.d. te vinden over bijna elk denkbaar onderwerp, en daar zitten kwalitatief uitstekende teksten bij.
Maar ik ben het er wel mee eens dat je Duits (en basisstatistiek) niet moet afdoen als zooi
Ik kom ook voor moderne onderwerpen nog wel Duits tegen, twee artikels in de afgelopen paar jaar.quote:
[..]
Bijna alle wetenschap gaat toch in het Engels? Volgens mij zijn er wel veel oude werken die alleen in het Duits te lezen zijn, dus voor jou is Duitse kennis onmisbaar. Maar als je moderne onderwerpen bestudeert heb je voor zover ik weet geen Duitse taal nodig.
Maar ik ben het er wel mee eens dat je Duits (en basisstatistiek) niet moet afdoen als zooi
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Oh grappig. Gingen die artikelen over statistiek/econometrie ?quote:
[..]
Ik kom ook voor moderne onderwerpen nog wel Duits tegen, twee artikels in de afgelopen paar jaar.
Tja, wat heet nodig? Kijk, ik bestudeer onderwerpen het liefst vanuit verschillende perspectieven en vanuit verschillende achtergronden, en er is echt ook heel veel moderne literatuur in het Duits. Dus waarom zou ik mezelf het gebruik van bronnen ontzeggen in andere talen dan het Engels of het Nederlands? In het Duitse universitaire wiskunde onderwijs zul je ook niet zo snel Engelstalige boeken zien, ook niet voor wat meer gevorderde onderwerpen. In Nederland gebeurt dat wel in toenemende mate, en dat vind ik geen goede ontwikkeling. Ik heb ook regelmatig het idee hier op FOK dat mensen een stukje wiskundige uitleg mede niet goed begrijpen omdat ze het Engels niet goed begrijpen, ook al denken ze prima Engels te kunnen lezen.quote:
[..]
Bijna alle wetenschap gaat toch in het Engels? Volgens mij zijn er wel veel oude werken die alleen in het Duits te lezen zijn, dus voor jou is Duitse kennis onmisbaar. Maar als je moderne onderwerpen bestudeert heb je voor zover ik weet geen Duitse taal nodig.
[ Bericht 0% gewijzigd door Riparius op 12-12-2012 17:46:47 ]
over wiskundige optimaliseringquote:
[..]
Oh grappig. Gingen die artikelen over statistiek/econometrie ?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik vind het juist wel goed dat er veel Engelse literatuur wordt gebruikt. De wetenschap is voornamelijk in het Engels, dus dan hoef je ook geen switch te maken als je Engelse wetenschappelijke artikelen gaat lezen.quote:
[..]
Tja, wat heet nodig? Kijk, ik bestudeer onderwerpen het liefst vanuit verschillende perspectieven en vanuit verschillende achtergronden, en er is echt ook heel veel moderne literatuur in het Duits. Dus waarom zou ik mezelf het gebruik van bronnen ontzeggen in andere talen dan het Engels of het Nederlands? In het Duitse universitaire wiskunde onderwijs zul je ook niet zo snel Engelstalige boeken zien, ook niet voor wat meer gevorderde onderwerpen. In Nederland gebeurt dat wel in toenemende mate, en dat ik vind ik geen goede ontwikkeling. Ik heb ook regelmatig het idee hier op FOK dat mensen een stukje wiskundige uitleg mede niet goed begrijpen omdat ze Engels niet goed begrijpen, ook al denken ze prima Engels te kunnen lezen.
Ik heb eerder dat ik een Nederlandse uitleg niet begrijp, omdat ik vaker de Engelse dan de Nederlandse term ken
.
Ja, ik begrijp je punt en ik zie ook wel de voordelen van het gebruik van Engelstalige leerboeken (sommige mensen hebben het over tekstboeken, maar dat is dan weer een anglicisme), maar er zijn ook nadelen. Het is me op de site van Hogendijk bijvoorbeeld opgevallen dat, hij, nu hij (van hogerhand?) wordt gedwongen te werken met het Engelstalige boek van Adams & Essex meteen al één van de eerste colleges uitluidt met een causerie over Nederlandse woorden in de wiskunde, en deze besluit met: Houd het Nederlands in ere! Ik zie daar een stil protest in.quote:
[..]
Ik vind het juist wel goed dat er veel Engelse literatuur wordt gebruikt. De wetenschap is voornamelijk in het Engels, dus dan hoef je ook geen switch te maken als je Engelse wetenschappelijke artikelen gaat lezen.
Ik heb eerder dat ik een Nederlandse uitleg niet begrijp, omdat ik vaker de Engelse dan de Nederlandse term ken
De hele discussie over de voor- en nadelen van het gebruik van een internationale taal is trouwens niet nieuw: in vroeger eeuwen vond het onderwijs aan de universiteiten, ook in Nederland, plaats in het Latijn en werden wetenschappelijke artikelen en boeken ook in het Latijn geschreven. Dat is eeuwenlang zo geweest, tot het Latijn plaats maakte voor de landstalen. In Frankrijk gebeurde dat al vrij vroeg, maar in bijvoorbeeld Duitsland was het zelfs tot in het midden van de 19e eeuw niet ongebruikelijk om in het Latijn te publiceren. Ik heb een beetje het idee dat we die hele discussie over de voor- en nadelen van het gebruik van een internationale taal nu dunnetjes over doen en dat men al lang is vergeten waarom het Latijn ooit af is geschaft als internationale wetenschapstaal.
[ Bericht 0% gewijzigd door Riparius op 11-12-2012 00:01:34 ]
Allemaal Esperanto leren 
[ Bericht 31% gewijzigd door Dale. op 11-12-2012 00:45:19 ]
Ik denk dat we daar niet te moeilijk over moeten denken. Er werd eenvoudig weg steeds minder les gegeven in het Latijn omdat studenten, wellicht te lui waren of doordat de universiteit steeds toegangelijker werd voor mensen die geen Latijn spraken en dat professor zich aanpaste aan de studenten die geen Latijn konden.quote:Ik heb een beetje het idee dat we die hele discussie over de voor- en nadelen van het gebruik van een internationale taal nu dunnetjes over doen en dat men al lang is vergeten waarom het Latijn ooit af is geschaft als internationale wetenschapstaal.
[ Bericht 31% gewijzigd door Dale. op 11-12-2012 00:45:19 ]
Ik zie nergens "Houd het Nederlands in ere!" staan.quote:
[..]
Ja, ik begrijp je punt en ik zie ook wel de voordelen van het gebruik van Engelstalige leerboeken (sommige mensen hebben het over tekstboeken, maar dat is dan weer een anglicisme), maar er zijn ook nadelen. Het is me op de site van Hogendijk bijvoorbeeld opgevallen dat, hij, nu hij (van hogerhand?) wordt gedwongen te werken met het Engelstalige boek van Adams & Essex meteen al één van de eerste colleges uitluidt met een causerie over Nederlandse woorden in de wiskunde, en deze besluit met: Houd het Nederlands in ere! Ik zie daar een stil protest in.
Lattijn ?quote:Op dinsdag 11 december 2012 00:21 schreef Dale. het volgende:
Allemaal Esperanto leren
[..]
Ik denk dat we daar niet te moeilijk over moeten denken. Er werd eenvoudig weg steeds minder les gegeven in het Lattijn omdat studenten, wellicht te lui waren of doordat de universiteit steeds toegangelijker werd voor mensen die geen Lattijn spraken en dat professor zich aanpaste aan de studenten die geen Lattijn konden.
Oepsquote:
[..]
Ik zie nergens "Houd het Nederlands in ere!" staan.
[..]
Lattijn ?
Hier, laatste pagina.quote:
[..]
Ik zie nergens "Houd het Nederlands in ere!" staan.
Mijn excuses, het is niet dat je uitleg onduidelijk is, het schort mij aan basiskennis over complexe functies en eigenschappen van zijn afgeleide.quote:
[..]
Denk ik toch anders over. Een goede leesvaardigheid Duits is heel nuttig als je verder wil met wiskunde. Er zijn massa's Duitse boeken, artikelen, dictaten e.d. te vinden over bijna elk denkbaar onderwerp, en daar zitten kwalitatief uitstekende teksten bij.
[..]
Vreemd, ik dacht dat ik het toch duidelijk had uitgelegd. Een analytische (of : holomorfe) functie geeft een (lokaal) conforme afbeelding. Lees anders nog eens in het boekje van Maor na (hier) hoe hij de Mercatorprojectie in verband brengt met de complexe logaritme.
Ik zal het doornemen.
Niet meer echt motivatie voor Duits. Basisstatistiek gaat dan nog wel..quote:
[..]
Bijna alle wetenschap gaat toch in het Engels? Volgens mij zijn er wel veel oude werken die alleen in het Duits te lezen zijn, dus voor jou is Duitse kennis onmisbaar. Maar als je moderne onderwerpen bestudeert heb je voor zover ik weet geen Duitse taal nodig.
Maar ik ben het er wel mee eens dat je Duits (en basisstatistiek) niet moet afdoen als zooi
Met uw permissie heb ik dit rechtstreeks in mijn werkstuk gezet, in plaats van te parafraseren. Alhoewel dat eigenlijk niet helemaal mag is dit wel de kortste manier, en ik moet een beetje op de lengte gaan letten.quote:
[..]
Het raakvlak aan punt P van de bol staat loodrecht op straal MP en het raakvlak aan punt N van de bol (i.e. het projectievlak) staat loodrecht op straal MN. Dus staan zowel zowel het raakvlak aan punt P als het projectievlak loodrecht op het vlak bepaald door de punten M, N en P. En aangezien WR in het projectievlak ligt en RA in het vlak bepaald door de punten M,N,P is dus WR ⟂ RA.
Lijkt me prima, het is geen originele gedachte maar gewoon heel eenvoudige stereometrie hoor: als eene lijn loodrecht staat op een vlak, dan zal elk vlak, dat door die lijn gaat, loodrecht op dat vlak staan. (link). Maar ja, wie leert er nog stereometrie?quote:Op dinsdag 11 december 2012 20:43 schreef Amoeba het volgende:
[..]
Met uw permissie heb ik dit rechtstreeks in mijn werkstuk gezet, in plaats van te parafraseren. Alhoewel dat eigenlijk niet helemaal mag is dit wel de kortste manier, en ik moet een beetje op de lengte gaan letten.
Daar gaan ook enkele colleges van Functies en Reeksen over. Als je eens een uurtje over hebt zou je kunnen kijken of je er wat van volgt (over het algemeen zijn hoorcolleges goed te volgen, zelfs als je niet echt alle voorkennis hebt) bij de webcolleges Functies en Reeksen. Het 9e college gaat over complexe differentieerbaarheid.quote:
[..]
Mijn excuses, het is niet dat je uitleg onduidelijk is, het schort mij aan basiskennis over complexe functies en eigenschappen van zijn afgeleide.
Ik zal het doornemen.
Even doorlezen. Dat was wel mijn enige gedachte erbij, mag je zeggen dat ieder vlak dat door diameter ON gaat loodrecht op WR staat? En dan bedoel ik niet 'verticaal loodrecht', maar juist horizontaal, ofwel de rechte hoek in het projectievlak.quote:
[..]
Lijkt me prima, het is geen originele gedachte maar gewoon heel eenvoudige stereometrie hoor: als eene lijn loodrecht staat op een vlak, dan zal elk vlak, dat door die lijn gaat, loodrecht op dat vlak staan. (link). Maar ja, wie leert er nog stereometrie?
Ik denk dat je een fout maakt. De hoek van 90 graden volgt niet uit dat WR in het projectievlak ligt, maar juist in het raakvlak r, want dat staat loodrecht op straal MR welk in vlak MNP ligt, en in dat vlak is RA dus ook vertegenwoordigd. Klopt dit?
[ Bericht 1% gewijzigd door #ANONIEM op 11-12-2012 21:19:21 ]
Nee, dat mag je niet zeggen want het klopt niet. Elk vlak door ON staat loodrecht op het projectievlak en WR ligt in het projectievlak, dat wel.quote:
[..]
Even doorlezen. Dat was wel mijn enige gedachte erbij, mag je zeggen dat ieder vlak dat door diameter ON gaat loodrecht op WR staat?
Dit is onduidelijk, ik begrijp niet wat je hier bedoelt.quote:En dan bedoel ik niet 'verticaal loodrecht', maar juist horizontaal, ofwel de rechte hoek in het projectievlak.
Ik denk dat er iets niet klopt aan je uitleg, zoals ik al stelde in mijn vorige post. Zoals jij het stelde leek dit wel zo..quote:
[..]
Nee, dat mag je niet zeggen want het klopt niet. Elk vlak door ON staat loodrecht op het projectievlak en WR ligt in het projectievlak, dat wel.
[..]
Dit is onduidelijk, ik begrijp niet wat je hier bedoelt.
Je hoeft alleen te constateren dat de lijnstukken WR en RA in twee verschillende vlakken liggen die loodrecht op elkaar staan om te kunnen concluderen dat ∠WRA = 90°. Lijnstuk WR ligt zowel in het projectievlak als in het raakvlak aan de bol in punt P, maar het projectievlak en dit raakvlak staan beide loodrecht op het vlak bepaald door de punten MNP waarin lijnstuk RA ligt.quote:
[..]
Ik denk dat je een fout maakt. De hoek van 90 graden volgt niet uit dat WR in het projectievlak ligt, maar juist in het raakvlak r, want dat staat loodrecht op straal MR welk in vlak MNP ligt, en in dat vlak is RA dus ook vertegenwoordigd. Klopt dit?
Zie een examinator maar eens in 20 minuten uit te leggen hoe zo'n projectie in elkaar steekt.
Dit is dus het nadeel van staatsexamen, je moet circa 80 uur in een profielwerkstuk geven, en daar naderhand een presentatie over geven. Hoe moet ik zo'n presentatie vorm geven? Een projectie behandelen? In het kort allemaal? Ik wil al enkel cilindrische projecties gaan doen, dus misschien een vergelijking opzetten. En het mooie is, ze krijgen die ochtend een stapel met profielwerkstukken, dus waarschijnlijk hebben ze 10 minuten tijd om het door te nemen. Al dat werk voor een half uurtje beoordeling.
Dit is dus het nadeel van staatsexamen, je moet circa 80 uur in een profielwerkstuk geven, en daar naderhand een presentatie over geven. Hoe moet ik zo'n presentatie vorm geven? Een projectie behandelen? In het kort allemaal? Ik wil al enkel cilindrische projecties gaan doen, dus misschien een vergelijking opzetten. En het mooie is, ze krijgen die ochtend een stapel met profielwerkstukken, dus waarschijnlijk hebben ze 10 minuten tijd om het door te nemen. Al dat werk voor een half uurtje beoordeling.
Dat is een beetje het nadeel van je met dingen bezighouden die wat ingewikkelder zijn dan het gemiddelde. Ik had op het vwo ook een profielwerkstuk waar ik echt een hele zooi werk in had zitten (het ging over muziek, en ik had me vooral gefocust op digitale muziek en signaalverwerking, digitale effecten en dat soort dingen, vond ik destijds heel leuk). Dat werkstuk bevatte ook redelijk wat wiskunde (ik heb er geloof ik ook behoorlijk wat Fouriertheorie in gestopt, wat wel nuttig is bij het begrijpen van geluid). Dat werkstuk ging ook richting de 100 pagina's. Kreeg ik van mijn beoordeler (een biologie-docent die geloof ik niet echt van wiskunde hield) doodleuk te horen dat hij het te ingewikkeld vond, en had hij me een 6 gegeven.quote:
Zie een examinator maar eens in 20 minuten uit te leggen hoe zo'n projectie in elkaar steekt.
Dit is dus het nadeel van staatsexamen, je moet circa 80 uur in een profielwerkstuk geven, en daar naderhand een presentatie over geven. Hoe moet ik zo'n presentatie vorm geven? Een projectie behandelen? In het kort allemaal? Ik wil al enkel cilindrische projecties gaan doen, dus misschien een vergelijking opzetten. En het mooie is, ze krijgen die ochtend een stapel met profielwerkstukken, dus waarschijnlijk hebben ze 10 minuten tijd om het door te nemen. Al dat werk voor een half uurtje beoordeling.
Ik was dan ook vrij pissig toen een jongen die zijn profielwerkstuk letterlijk in één avond had geschreven (16 pagina's, veel plaatjes en witte bladzijden), flink hoger had dan ik (hij had geloof ik een 7 of 8, in ieder geval een 7 of hoger). Daarna heb ik het er nog met mijn beoordeler over gehad, en nadat hij overlegd heeft met een natuurkundedocent heb ik toch een 7 gekregen.
Mijn eigen docenten mogen me niet eens beoordelen. Ik moet mijn profielwerkstuk opsturen naar DUO/IB, begin mei ofzo. Er wordt iemand aangewezen om mij te examineren betreffende het profielwerkstuk. Als hij hier aankomt op school, een docent van een andere school, nooit die van mijzelf, krijgt hij de profielwerkstukken van de leerlingen die hij moet examineren. Nou goed, hele dag examineren en tussendoor de werkstukken doornemen. Je ziet 'm al hangen hé.?quote:
[..]
Dat is een beetje het nadeel van je met dingen bezighouden die wat ingewikkelder zijn dan het gemiddelde. Ik had op het vwo ook een profielwerkstuk waar ik echt een hele zooi werk in had zitten (het ging over muziek, en ik had me vooral gefocust op digitale muziek en signaalverwerking, digitale effecten en dat soort dingen, vond ik destijds heel leuk). Dat werkstuk bevatte ook redelijk wat wiskunde (ik heb er geloof ik ook behoorlijk wat Fouriertheorie in gestopt, wat wel nuttig is bij het begrijpen van geluid). Dat werkstuk ging ook richting de 100 pagina's. Kreeg ik van mijn beoordeler (een biologie-docent die geloof ik niet echt van wiskunde hield) doodleuk te horen dat hij het te ingewikkeld vond, en had hij me een 6 gegeven.
Ik was dan ook vrij pissig toen een jongen die zijn profielwerkstuk letterlijk in één avond had geschreven (16 pagina's, veel plaatjes en witte bladzijden), flink hoger had dan ik (hij had geloof ik een 7 of 8, in ieder geval een 7 of hoger). Daarna heb ik het er nog met mijn beoordeler over gehad, en nadat hij overlegd heeft met een natuurkundedocent heb ik toch een 7 gekregen.
Dat krijg ik trouwens ook altijd te horen. Wat ik doe is te ingewikkeld, hij begrijpt het niet en blijft dan ook uitstellen. Volgende week dinsdag heb ik vastgepind, dan stuur ik hem een verzameling documentatie die hij door mag nemen.
[ Bericht 5% gewijzigd door #ANONIEM op 11-12-2012 23:21:16 ]
Kan iemand mij stock en cash dividend uitleggen. Heb morgen SE, maar ben het weer vergeten. Je moet de cash en stock dividend percentages bij elkaar optellen, en dan dit getal van het geplaatst AK. Maar verder weer ik het niet.. Cash was belasting en Stock niet. Ik mis 1 of 2 stapjes, als iemand me die even zou kunnen uitleggen.. Bedankt!
hoe heet dit topic?quote:
Kan iemand mij stock en cash dividend uitleggen. Heb morgen SE, maar ben het weer vergeten. Je moet de cash en stock dividend percentages bij elkaar optellen, en dan dit getal van het geplaatst AK. Maar verder weer ik het niet.. Cash was belasting en Stock niet. Ik mis 1 of 2 stapjes, als iemand me die even zou kunnen uitleggen.. Bedankt!
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Riparius, bij de Mercatorprojectie worden de cartesische coördinaten gegeven door
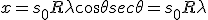
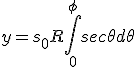
Als ik x/y neem, volgt daar dan direct uit dat de projectie conform is? Aangezien de secans toch ook een schaalfactor in verticale richting is?
Of maak ik hier een (fundamentele) denkfout?
[ Bericht 2% gewijzigd door #ANONIEM op 12-12-2012 14:14:42 ]
Als ik x/y neem, volgt daar dan direct uit dat de projectie conform is? Aangezien de secans toch ook een schaalfactor in verticale richting is?
Of maak ik hier een (fundamentele) denkfout?
[ Bericht 2% gewijzigd door #ANONIEM op 12-12-2012 14:14:42 ]
Aha dank je wel!quote:
[..]
Het klassieke ε/3 trucje. Het bewijs staat vast wel ergens in de een of andere vorm in je leerboek, en anders moet je maar even hier kijken.
Ik heb nog een vraagje:
als ik een functie v(x,t) met x in ]0,L[ en t in ]0,+oneindig[ heb, die ik kan schrijven als:
(1/2)*(f(x+at)+f(x-at)) met a een constante, die niet 0 is.
En ik weet bovendien dat in het gegeven gebied v(x,t) continu is, mag ik dan concluderen dat f continu is in heel R? Volgens de cursus kan dit, maar ik zie niet direct in waarom.
Je maakt een fundamentele denkfout.quote:
Riparius, bij de Mercatorprojectie worden de cartesische coördinaten gegeven door
Als ik x/y neem, volgt daar dan direct uit dat de projectie conform is? Aangezien de secans toch ook een schaalfactor in verticale richting is?
Of maak ik hier een (fundamentele) denkfout?
Laten we zeggen dat we een punt op aarde hebben met geografische coördinaten (λ;φ) waarbij λ in radialen wordt uitgedrukt (positief voor oosterlengte, negatief voor westerlengte) en dat φ eveneens in radialen wordt uitgedrukt (positief voor noorderbreedte en negatief voor zuiderbreedte). Laten we verder zeggen dat dit punt met geografische coördinaten (λ;φ) op de Mercatorprojectie wordt afgebeeld als het punt met (cartesische) coördinaten (x;y). En laten we de horizontale en de verticale schaalfactoren voor het punt met geografische coördinaten (λ;φ) op onze kaart aangeven met resp. sh(λ;φ) en sv(λ;φ). Voor een conforme (hoekgetrouwe) afbeelding moet dan gelden sh(λ;φ) = sv(λ;φ) voor elk punt (λ;φ). Om dit aan te tonen berekenen we nu sh(λ;φ) en sv(λ;φ) zoals die volgen uit bovenstaande formules.
Eerst de horizontale schaalfactor voor het punt met geografische coördinaten (λ;φ). Verplaatsen we ons op aarde in oost-west richting van een punt met coördinaten (λ;φ) naar een punt met coördinaten (λ+Δλ;φ), waarbij je moet bedenken dat Δλ zowel positief kan zijn (verplaatsing in oostelijke richting) als negatief (verplaatsing in westelijke richting), dan leggen we op aarde een afstand af die, afgezien van het teken, R∙cosφ∙Δλ bedraagt. Laten we de (geörienteerde) afstand langs de breedtecirkel tot de nulmeridiaan a noemen, dan kunnen we de afgelegde afstand aangeven met Δa = R∙cosφ∙Δλ, waarbij Δa weer zowel positief kan zijn (verplaatsing in oostelijke richting) als negatief (verplaatsing in westelijke richting). Als nu op de kaart het punt (λ+Δλ;φ) wordt afgebeeld op het punt met cartesische coördinaten (x+Δx;y), dan bedraagt de horizontale schaalfactor voor het punt (λ;φ)
dus:
sh(λ;φ) = Δx/Δa = Δx/(R∙cosφ∙Δλ) = (1/(R∙cosφ))∙(Δx/Δλ) = (1/(R∙cosφ))∙s0∙R = s0∙sec φ
Nu de verticale schaalfactor voor het punt met geografische coördinaten (λ;φ). Verplaatsen we ons in noord-zuid richting naar een punt op aarde met geografische coördinaten (λ;φ+Δφ) waarbij Δφ weer zowel positief kan zijn (verplaatsing in noordelijke richting) als negatief (verplaatsing in zuidelijke richting), en noemen we de wijziging in de (geörienteerde) afstand a tot de evenaar Δa, dan is Δa = R∙Δφ. Als nu op de kaart het punt met geografische coördinaten (λ;φ+Δφ) wordt afgebeeld op een punt met cartesische coördinaten (x;y+Δy), dan bedraagt de verticale schaalfactor over deze afstand Δy/Δa = Δy/(R∙Δφ) = (1/R)∙Δy/Δφ, alleen is dit een gemiddelde schaalfactor voor de afbeelding op de kaart van het traject van (λ;φ) naar (λ;φ+Δφ), omdat Δy/Δφ geen constante is maar afhangt van φ. Om de verticale schaalfactor in het punt (λ;φ) op de kaart te bepalen moeten we de limiet nemen van de trajectschaling Δy/Δa voor Δφ → 0, dus dy/da = (1/R)∙dy/dφ. Voor de verticale schaalfactor op de kaart in het punt met geografische coördinaten (λ;φ) krijgen we dus:
sv(λ;φ) = (1/R)∙dy/dφ = (1/R)∙s0∙R∙sec φ = s0∙sec φ
Zoals je ziet hebben we dus sh(λ;φ) = sv(λ;φ), QED.
[ Bericht 0% gewijzigd door Riparius op 13-12-2012 20:39:53 ]
Je redenering kan ik volgen. Alleen het vetgedrukte, ik zie je dat wel vaker zeggen, wat bedoel je daar precies mee?quote:
[..]
Je maakt een fundamentele denkfout.
Laten we zeggen dat we een punt op aarde hebben met geografische coördinaten (λ;φ) waarbij λ in radialen wordt uitgedrukt (positief voor oosterlengte, negatief voor westerlengte) en dat φ eveneens in radialen wordt uitgedrukt (positief voor noorderbreedte en negatief voor zuiderbreedte). Laten we verder zeggen dat dit punt met geografische coördinaten (λ;φ) op de Mercatorprojectie wordt afgebeeld als het punt met (cartesische) coördinaten (x;y). En laten we de horizontale en de verticale schaalfactoren voor het punt met geografische coördinaten (λ;φ) op onze kaart aangeven met resp. sh(λ;φ) en sv(λ;φ). Voor een conforme (hoekgetrouwe) afbeelding moet dan gelden sh(λ;φ) = sv(λ;φ) voor elk punt (λ;φ). Om dit aan te tonen berekenen we nu sh(λ;φ) en sv(λ;φ) zoals die volgen uit bovenstaande formules.
Eerst de horizontale schaalfactor voor het punt met geografische coördinaten (λ;φ). Verplaatsen we ons op aarde in oost-west richting van een punt met coördinaten (λ;φ) naar een punt met coördinaten (λ+Δλ;φ), waarbij je moet bedenken dat Δλ zowel positief kan zijn (verplaatsing in oostelijke richting) als negatief (verplaatsing in westelijke richting), dan leggen we op aarde een afstand af die, afgezien van het teken, R∙cosφ∙Δλ bedraagt. Laten we de (geörienteerde) afstand langs de breedtecirkel tot de nulmeridiaan a noemen, dan kunnen we de afgelegde afstand aangeven met Δa = R∙cosφ∙Δλ, waarbij Δa weer zowel positief kan zijn (verplaatsing in oostelijke richting) als negatief (verplaatsing in westelijke richting). Als nu op de kaart het punt (λ+Δλ;φ) wordt afgebeeld op het punt met cartesische coördinaten (x+Δx;y), dan bedraagt de horizontale schaalfactor voor het punt (λ;φ)
dus:
sh(λ;φ) = Δx/Δa = Δx/(R∙cosφ∙Δλ) = (1/(R∙cosφ))∙(Δx/Δλ) = (1/(R∙cosφ))∙s0∙R = s0∙sec φ
Nu de verticale schaalfactor voor het punt met geografische coördinaten (λ;φ). Verplaatsen we ons in noord-zuid richting naar een punt op aarde met geografische coördinaten (λ;φ+Δφ) waarbij Δφ weer zowel positief kan zijn (verplaatsing in noordelijke richting) als negatief (verplaatsing in zuidelijke richting), en noemen we de wijziging in de (geörienteerde) afstand a tot de evenaar Δa, dan is Δa = R∙Δφ. Als nu op de kaart het punt met geografische coördinaten (λ;φ+Δφ) wordt afgebeeld op een punt met cartesische coördinaten (x;y+Δy), dan bedraagt de verticale schaalfactor over deze afstand Δy/Δa = Δy/(R∙Δφ) = (1/R)∙Δy/Δφ, alleen is dit een gemiddelde schalingsfactor voor de afbeelding op de kaart van het traject van (λ;φ) naar (λ;φ+Δφ), omdat Δy/Δφ geen constante is maar afhangt van φ. Om de de verticale schalingsfactor in het punt (λ;φ) op de kaart te bepalen moeten we de limiet nemen van de trajectschaling Δy/Δa voor Δφ → 0, dus dy/da = (1/R)∙dy/dφ. Voor de verticale schaalfactor op de kaart in het punt met geografische coördinaten (λ;φ) krijgen we dus:
sv(λ;φ) = (1/R)∙dy/dφ = (1/R)∙s0∙R∙sec φ = s0∙sec φ
En zoals je ziet hebben we dus sh(λ;φ) = sv(λ;φ), QED.
Je weet niet of het + of - is. De richting is dus onbekend (zoals Riparius daarvoor uitlegt), maar de afstand niet.quote:
[..]
Je redenering kan ik volgen. Alleen het vetgedrukte, ik zie je dat wel vaker zeggen, wat bedoel je daar precies mee?
gr gr
Oh zo, moet je dit vermelden?quote:
[..]
Je weet niet of het + of - is. De richting is dus onbekend (zoals Riparius daarvoor uitlegt), maar de afstand niet.
Ja, want afstanden zijn niet negatief, terwijl Δa wel negatief kan zijn. Echter is Δa alleen negatief als Δλ resp. Δφ negatief is, en dan zijn ook Δx resp. Δy negatief, zodat de schaalfactoren Δx/Δa en Δy/Δa dus altijd positief zijn.quote:
Ik kom bij een vraagstuk niet uit. Het gaat over een vector F projecteren op v:
vector v = 3i + 4j
vector F = 4i + j
a) Vind de component van F parallel aan v
b) Vind de component van F loodrecht aan v
c) Vind de arbeid W gedaan door kracht F door de verplaatsing van v
antwoorden zijn:
a) 1.92i + 2.56j
b) 2.08i - 1.56j
c) W= 16
Met de formule van F= Fparallel + Fperpendicular klopt a en b iniedergeval wel. Zou iemand me kunnen laten zien hoe je deze sommen maakt?
Bvd
vector v = 3i + 4j
vector F = 4i + j
a) Vind de component van F parallel aan v
b) Vind de component van F loodrecht aan v
c) Vind de arbeid W gedaan door kracht F door de verplaatsing van v
antwoorden zijn:
a) 1.92i + 2.56j
b) 2.08i - 1.56j
c) W= 16
Met de formule van F= Fparallel + Fperpendicular klopt a en b iniedergeval wel. Zou iemand me kunnen laten zien hoe je deze sommen maakt?
Bvd
Vraagje... Is er een methode waarmee ik kan bepalen hoeveel invloed het veranderen van iedere parameter heeft op een functie?
Bijvoorbeeld; y = f(x) = 1/a*(b*c*d*x^2 + e*f*g)*x + h
Ik weet bijvoorbeeld dat a ergens tussen 0.7 en 0.85 ligt. Dit weet ik voor iedere parameter. Nu wil ik zeg maar kunnen afleiden hoeveel invloed iedere parameter heeft op het eind antwoord. Zorgt a verandering van a bijvoorbeeld dat het antwoord omhoog schiet of juist maar een klein beetje omhoog schiet.
Bijvoorbeeld; y = f(x) = 1/a*(b*c*d*x^2 + e*f*g)*x + h
Ik weet bijvoorbeeld dat a ergens tussen 0.7 en 0.85 ligt. Dit weet ik voor iedere parameter. Nu wil ik zeg maar kunnen afleiden hoeveel invloed iedere parameter heeft op het eind antwoord. Zorgt a verandering van a bijvoorbeeld dat het antwoord omhoog schiet of juist maar een klein beetje omhoog schiet.
Een partiële afgeleide komt denk ik nog het dichtst in de buurt van wat jij bedoelt (hoewel er omstandigheden te bedenken zijn waarin de partiële afgeleide groot en de invloed op de functie slechts klein). Of had je daar al over nagedacht?quote:Op donderdag 13 december 2012 00:29 schreef Dale. het volgende:
Vraagje... Is er een methode waarmee ik kan bepalen hoeveel invloed het veranderen van iedere parameter heeft op een functie?
Bijvoorbeeld; y = f(x) = 1/a*(b*c*d*x^2 + e*f*g)*x + h
Ik weet bijvoorbeeld dat a ergens tussen 0.7 en 0.85 ligt. Dit weet ik voor iedere parameter. Nu wil ik zeg maar kunnen afleiden hoeveel invloed iedere parameter heeft op het eind antwoord. Zorgt a verandering van a bijvoorbeeld dat het antwoord omhoog schiet of juist maar een klein beetje omhoog schiet.
Anders zou je kunnen kijken naar het bereik van de functie als je a varieert en de anderen variabelen vast laat, maar dat is een stuk ingewikkelder. Misschien zijn er nog andere methoden, dit is wat ik zo even snel kan bedenken.
Maak eens een plaatje met de vectoren. Gebruik dat voor het inproduct tussen twee vectoren a en b geldt:quote:
Ik kom bij een vraagstuk niet uit. Het gaat over een vector F projecteren op v:
vector v = 3i + 4j
vector F = 4i + j
a) Vind de component van F parallel aan v
b) Vind de component van F loodrecht aan v
c) Vind de arbeid W gedaan door kracht F door de verplaatsing van v
antwoorden zijn:
a) 1.92i + 2.56j
b) 2.08i - 1.56j
c) W= 16
Met de formule van F= Fparallel + Fperpendicular klopt a en b iniedergeval wel. Zou iemand me kunnen laten zien hoe je deze sommen maakt?
Bvd
waarbij alfa de hoek tussen a en b is.
Voor c gebruik je dat de arbeid gegeven wordt door het inproduct tussen kracht en snelheid.
Bepaal eerst een vector w die loodrecht staat op v. Aangezien (3;4) het eindpunt is van vector v en een punt (a;b) bij rotatie om de oorsprong over een rechte hoek tegen de klok in overgaat in het punt met coördinaten (b;-a) hebben we dan w = 4i - 3j. Nu willen we vector F schrijven als een lineaire combinatie van v en w, dus:quote:
Ik kom bij een vraagstuk niet uit. Het gaat over een vector F projecteren op v:
vector v = 3i + 4j
vector F = 4i + j
a) Vind de component van F parallel aan v
b) Vind de component van F loodrecht aan op v
c) Vind de arbeid W gedaan door kracht F door bij de verplaatsing van v
antwoorden zijn:
a) 1.92i + 2.56j
b) 2.08i - 1.56j
c) W = 16
Met de formule van F= Fparallel + Fperpendicular klopt a en b in ieder geval wel. Zou iemand me kunnen laten zien hoe je deze sommen opgaven maakt?
Bvd
F = λ∙v + μ∙w
Dit geeft:
4i + j = λ∙(3i + 4j) + μ∙(4i - 3j)
Uitwerken geeft nu:
4i + j = (3λ + 4μ)i + (4λ - 3μ)j
En dus moet gelden:
3λ + 4μ = 4
4λ - 3μ = 1
Oplossen van dit lineaire stelsel geeft λ = 16/25 en μ = 13/25.
De component van F parallel aan v is dus:
λ∙v = 16/25 ∙ (3i + 4j) = 48/25 ∙ i + 64/25 ∙ j
En de component van F loodrecht op v (en parallel aan w) is dus:
μ∙w = 13/25 ∙ (4i - 3j) = 52/25 ∙ i - 39/25 ∙ j
Om nu de arbeid W gedaan door kracht F bij een verplaatsing langs v te berekenen kun je natuurlijk de lengte van de component van F langs v vermenigvuldigen met de lengte van v en dan vind je W = 5∙√((48/25)2 + (64/25)2) = 5 ∙ 16/5 = 16. Maar het is veel eenvoudiger om het inproduct te nemen van F en v, dan hebben we direct:
W = F∙v = (4i + j)∙(3i + 4j) = 4∙3 + 1∙4 = 16
[ Bericht 0% gewijzigd door Riparius op 13-12-2012 02:33:20 ]
Ja had al aan partiële afgeleide gedacht. maar nog niet verder naar gekeken vanwege de reden die je zelf al opnoemt.quote:
[..]
Een partiële afgeleide komt denk ik nog het dichtst in de buurt van wat jij bedoelt (hoewel er omstandigheden te bedenken zijn waarin de partiële afgeleide groot en de invloed op de functie slechts klein). Of had je daar al over nagedacht?
Anders zou je kunnen kijken naar het bereik van de functie als je a varieert en de anderen variabelen vast laat, maar dat is een stuk ingewikkelder. Misschien zijn er nog andere methoden, dit is wat ik zo even snel kan bedenken.
Probleem is dat ik een dataset heb. Hier moet een theoretische functie op gefit worden. Ik weet van alle variabelen wat deze ongeveer, minimum waarde en maximum waarde, zijn. Echter met de huidige bounderies op m'n variabelen krijg ik hem niet gefit.
Nu wil ik zeg maar soort van berekenen hoe groot de kans is dat de waarde van een bepaalde variabele fout is. Een aantal kan ik vrijwel meteen wegstrepen maar 4 variabelen niet.
Ik zit al even met de volgende som, snap niet helemaal wat de weg er naartoe is:
Een beweging van een element is als volgt:
Nu moet de snelheid mbv de spatial/eulerian description berekend worden.
De eerste component komt uit op:
Echter snap ik niet hoe je hier systematisch precies op komt.
Een beweging van een element is als volgt:
Nu moet de snelheid mbv de spatial/eulerian description berekend worden.
De eerste component komt uit op:
Echter snap ik niet hoe je hier systematisch precies op komt.
Kan iemand uitleggen waarom een rotatie matrix is zoals hij is:
http://nl.wikipedia.org/wiki/Rotatiematrix
Ik ben bezig aan een 3d engine maar nu ik bij rotaties uitkom vraag ik me af waarom dit werkt.. al googlend kom ik op filmpjes van mensen die het voordoen, maar niet die het uitleggen..
iemand?
http://nl.wikipedia.org/wiki/Rotatiematrix
Ik ben bezig aan een 3d engine maar nu ik bij rotaties uitkom vraag ik me af waarom dit werkt.. al googlend kom ik op filmpjes van mensen die het voordoen, maar niet die het uitleggen..
iemand?
Ik zal dit simpel uitleggenquote:
iemand uitleggen waarom een rotatie matrix is zoals hij is:
http://nl.wikipedia.org/wiki/Rotatiematrix
Ik ben bezig aan een 3d engine maar nu ik bij rotaties uitkom vraag ik me af waarom dit werkt.. al googlend kom ik op filmpjes van mensen die het voordoen, maar niet die het uitleggen..
iemand?
Probeer zelf een simpele vector (x,y) linksom te roteren met een 2 keer 2 matrix, zodat de vector zijn lengte behoudt.
Je kunt ook dan vervolgens vectoren als (x,y,z) roteren door drie keer één as niet te roteren (drie rotaties), dus met die rotatie matrices in jouw link voor in de drie dimensies.
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Bedankt, dat had ik doorquote:
[..]
Ik zal dit simpel uitleggen
Probeer zelf een simpele vector (x,y) linksom te roteren met een 2 keer 2 matrix, zodat de vector zijn lengte behoudt.
Je kunt ook dan vervolgens vectoren als (x,y,z) roteren door drie keer één as niet te roteren (drie rotaties), dus met die rotatie matrices in jouw link voor in de drie dimensies.
De vraag is dat ook meer hoe ze op die gonio komen.
Kijk eens op welke punten [1 0 0], [0 1 0] en [0 0 1] terecht moeten komen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
pff voel me best dom maar ga het toch vragen:
Ik heb de partieel afgeleiden van L en K nodig van :
/niet zozeer nodig, ik heb ze wel, maar de stappen hoe ze er aan komen is mij nogal vaag
Ik heb de partieel afgeleiden van L en K nodig van :
/niet zozeer nodig, ik heb ze wel, maar de stappen hoe ze er aan komen is mij nogal vaag
Oké, je snapt dan hoe je van 2 dimensies naar 3 dimensies gaat. Dus het is genoeg om alleen 2 dimensies te behandelen.quote:
[..]
Bedankt, dat had ik door
Je wil vectoren roteren en omdat je wil dat de vectoren niet van lengte veranderen, roteer je ze over de éénheidscirkel. Dus teken een goniometrische cirkel zoals op de middelbare school, http://commons.wikimedia.(...)e-cirkel-sin-cos.png. Beschouw twee verschillende hoeken en druk de bijbehorende x en y component uit in zijn hoek met de sinus en cosinus. Bekijk vervolgens hoe je van de ene x naar de andere x gaat. Doe hetzelfde voor de y.
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Herschrijf je uitdrukking eens alsquote:
pff voel me best dom maar ga het toch vragen:
Ik heb de partiële afgeleiden van naar L en K nodig van :
[ afbeelding ]
/niet zozeer nodig, ik heb ze wel, maar de stappen hoe ze er aan komen is mij nogal vaag
2∙K1/2∙L3/2
Nu zie je toch wel hoe je ∂(2∙K1/2∙L3/2)/∂K en ∂(2∙K1/2∙L3/2)/∂L bepaalt?
quote:
Kijk eens op welke punten [1 0 0], [0 1 0] en [0 0 1] terecht moeten komen.
Ik ben niet heel handig met die sinussenquote:
[..]
Oké, je snapt dan hoe je van 2 dimensies naar 3 dimensies gaat. Dus het is genoeg om alleen 2 dimensies te behandelen.
Je wil vectoren roteren en omdat je wil dat de vectoren niet van lengte veranderen, roteer je ze over de éénheidscirkel. Dus teken een goniometrische cirkel zoals op de middelbare school, http://commons.wikimedia.(...)e-cirkel-sin-cos.png. Beschouw twee verschillende hoeken en druk de bijbehorende x en y component uit in zijn hoek met de sinus en cosinus. Bekijk vervolgens hoe je van de ene x naar de andere x gaat. Doe hetzelfde voor de y.
Als ik iets roteer over de eenheidscirkel dan krijg je uiteraard x=cos(a) en y=sin(a). dit geldt voor vector: [1,0] als in [x,y] nu lijkt het mij logisch dat een zelfde draaiing er voor zorgt dat de vector [0,1] dan hetzelfde krijgt maar 90 graden verder terecht komt, wat neerkomt op de afgeleides van cos en sin. Nogmaals, ik faal hier nogal mee, denk ik enigsinds in de juiste richting?
oohhh easy money, zo, bedankt. Die notatiewijze van mij is ook nooit zo denderend trouwensquote:
[..]
Herschrijf je uitdrukking eens als
2∙K1/2∙L3/2
Nu zie je toch wel hoe je ∂(2∙K1/2∙L3/2)/∂K en ∂(2∙K1/2∙L3/2)/∂L bepaalt?
(van ipv naar etc)
Hm nee daar klopte waarschijnlijk niet veel van. Het probleem is een beetje dat ik als eerstejaars een tweedejaarsvak als keuze heb gekozen, terwijl je voor dit vak eigenlijk lineaire algebra nodig had als voorkennis..
Ik ben zelf aan het blunderen. Je roteert gewoon over een cirkel en niet per se over de éénheidscirkel. Je leert dit niet bij de vak lineaire algebra. De opgave dat ik je gaf, ziet er niet echt prettig uit (nu ik het zelf probeer). Sorry, ik heb zelf niet echt veel tijd om je te helpen. Je moet daarom op Riparius wachten, die wil je vast wel helpen.quote:Op zondag 16 december 2012 16:59 schreef dramatic het volgende:
Hm nee daar klopte waarschijnlijk niet veel van. Het probleem is een beetje dat ik als eerstejaars een tweedejaarsvak als keuze heb gekozen, terwijl je voor dit vak eigenlijk lineaire algebra nodig had als voorkennis..
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Precies dat ja. Vervolgens kun je een vector [a; b] schrijven als a*[1; 0] + b*[0; 1], en dan moet je kijken wat er gebeurt als je dit met de rotatiematrix vermenigvuldigt.quote:
[..]
[..]
Ik ben niet heel handig met die sinussen
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Het heeft uiteindelijk te maken met de definities van de cosinus en de sinus aan de hand van de eenheidscirkel. Je kunt ook heel fraai met vectoren werken om in te zien hoe de coördinaten (x;y) van een punt P zijn gerelateerd aan de coördinaten (x';y') van het beeld P' van P bij een rotatie om de oorsprong over een hoek θ.quote:
[..]
[..]
Ik ben niet heel handig met die sinussen
Je weet dat de vectoren ex en ey met lengte één langs de positieve x-as resp. langs de positieve y-as een (orthonormale) basis vormen voor de cartesische coördinaten. Hebben we nu de vector p = OP met als eindpunt P(x;y), dan geldt dus:
(1) p = x∙ex + y∙ey
Laten we zeggen dat de basis {ex,ey} bij een rotatie om de oorsprong over een hoek θ overgaat in {ex',ey'} en dat vector p daarbij overgaat in vector p'. Dan geldt dus:
(2) p' = x∙ex' + y∙ey'
Als we nu de beeldvectoren ex' en ey' uit kunnen drukken in ex en ey, dan kunnen we die uitdrukkingen invullen in (2) en zo dus de coördinaten van het eindpunt van vector p' oftewel de coördinaten (x';y') van het beeldpunt P' uitdrukken in de coördinaten (x;y) van punt P.
Welnu, het eindpunt (1;0) van vector ex gaat bij rotatie om de oorsprong over een hoek θ per definitie over in een punt met coördinaten (cos θ ; sin θ). Dat is een rechtstreekse consequentie van de definitie van de cosinus en de sinus aan de hand van de eenheidscirkel. Dus hebben we:
(3) ex' = cos θ ∙ ex + sin θ ∙ ey
Het is iets lastiger te zien hoe je ey' uit kunt drukken in ex en ey, maar bekijk dit eens als volgt. Als we de basis {ex,ey} roteren over een rechte hoek tegen de klok in, dan gaat vector ex over in vector ey en gaat vector ey over in vector -ex. Kiezen we nu even {ey,-ex} als basis, dan heeft het eindpunt van vector ey in deze basis de coördinaten (1;0), zodat het beeld van ey bij rotatie om de oorsprong over een hoek θ dus een vector ey' geeft waarvan de coördinaten van het eindpunt in deze basis weer per definitie gelijk zijn aan (cos θ ; sin θ), zodat dus geldt:
ey' = cos θ ∙ ey + sin θ ∙ (-ex)
En omdat sin θ ∙ (-ex) = -sin θ ∙ ex hebben we dus:
(4) ey' = cos θ ∙ ey - sin θ ∙ ex
Door nu (3) en (4) te substitueren in (2) krijgen we dus:
(5) p' = x∙(cos θ ∙ ex + sin θ ∙ ey) + y∙(cos θ ∙ ey - sin θ ∙ ex)
En door (5) uit te werken en de termen met ex en ey weer te hergroeperen krijgen we dan:
(6) p' = (x∙cos θ - y∙sin θ)∙ex + (x∙sin θ + y∙cos θ)∙ey
En aangezien voor de coördinaten (x';y') van het eindpunt P' van vector OP' = p' geldt p' = x'∙ex + y'∙ey hebben we dus:
(7a) x' = x∙cos θ - y∙sin θ
(7b) y' = x∙sin θ + y∙cos θ
Het is uiteraard ook mogelijk om omgekeerd de coördinaten (x;y) van het origineel P uit te drukken in de coördinaten (x';y') van het beeld P' en dat zou je kunnen doen door x en y op te lossen uit (7a) en (7b). Maar je kunt ook bedenken dat punt P'(x';y') weer overgaat in punt P(x;y) bij een rotatie om de oorsprong over een hoek -θ, zodat we door verwisseling van (x;y) en (x';y') en met gebruik van de identiteiten cos(-θ) = cos θ en sin(-θ) = -sin θ uit (7a) en (7b) direct kunnen afleiden dat ook geldt:
(8a) x = x'∙cos θ + y'∙sin θ
(8b) y = -x'∙sin θ + y'∙cos θ
Je opmerking dat differentiatie van de cosinus en de sinus functies beantwoordt aan een rotatie over een rechte hoek tegen de klok in is overigens juist, zie ook hier.
[ Bericht 0% gewijzigd door Riparius op 18-12-2012 18:25:31 ]
Erg veel dank voor deze uitvoerige uitleg!quote:
[..]
Het heeft uiteindelijk te maken met de definities van de cosinus en de sinus aan de hand van de eenheidscirkel. Je kunt ook heel fraai met vectoren werken om in te zien hoe de coördinaten van het beeld van een punt P(x;y) zijn gerelateerd aan de coördinaten van het beeldpunt P'(x';y') bij rotatie om de oorsprong over een hoek θ.
Je weet dat de vectoren ex en ey met lengte één langs de positieve x-as resp. langs de positieve y-as een (orthonormale) basis vormen voor de cartesische coördinaten. Hebben we nu de vector p = OP met als eindpunt P(x;y), dan geldt dus:
(1) p = x∙ex + y∙ey
Laten we zeggen dat de basis {ex,ey} bij een rotatie om de oorsprong over een hoek θ overgaat in {ex',ey'} en dat vector p daarbij overgaat in vector p'. Dan geldt dus:
(2) p' = x∙ex' + y∙ey'
Als we nu de beeldvectoren ex' en ey' uit kunnen drukken in ex en ey, dan kunnen we we die uitdrukkingen invullen in (2) en zo dus de coördinaten van het eindpunt van vector p' oftewel de coördinaten (x';y') van het beeldpunt P' uitdrukken in de coördinaten (x;y) van punt P.
Welnu, het eindpunt (1;0) van vector ex gaat bij rotatie om de oorsprong over een hoek θ per definitie over in een punt met coördinaten (cos θ ; sin θ). Dat is een rechtstreekse consequentie van de definitie van de cosinus en de sinus aan de hand van de eenheidscirkel. Dus hebben we:
(3) ex' = cos θ ∙ ex + sin θ ∙ ey
Het is iets lastiger te zien hoe je ey' uit kunt drukken in ex en ey, maar bekijk dit eens als volgt. Als we de basis {ex,ey} roteren over een rechte hoek tegen de klok in, dan gaat vector ex over in vector ey en gaat vector ey over in vector -ex. Kiezen we nu even {ey,-ex} als basis, dan heeft het eindpunt van vector ey in deze basis de coördinaten (1;0), zodat het beeld van ey bij rotatie om de oorsprong over een hoek θ dus een vector ey' geeft waarvan de coördinaten van het eindpunt in deze basis weer per definitie gelijk zijn aan (cos θ ; sin θ), zodat dus geldt:
ey' = cos θ ∙ ey + sin θ ∙ (-ex)
En omdat sin θ ∙ (-ex) = -sin θ ∙ ex hebben we dus:
(4) ey' = cos θ ∙ ey - sin θ ∙ ex
Door nu (3) en (4) te substitueren in (2) krijgen we dus:
(5) p' = x∙(cos θ ∙ ex + sin θ ∙ ey) + y∙(cos θ ∙ ey - sin θ ∙ ex)
En door (5) uit te werken en de termen met ex en ey weer te hergroeperen krijgen we dan:
(6) p' = (x∙cos θ - y∙sin θ)∙ex + (x∙sin θ + y∙cos θ)∙ey
En aangezien voor de coördinaten (x';y') van het eindpunt P' van vector OP' = p' geldt p' = x'∙ex + y'∙ey hebben we dus:
(7a) x' = x∙cos θ - y∙sin θ
(7b) y' = x∙sin θ + y∙cos θ
Het is uiteraard ook mogelijk om omgekeerd de coördinaten van het origineel P(x;y) uit te drukken in de coördinaten van het beeld P'(x';y') en dat zou je kunnen doen door x en y op te lossen uit (7a) en (7b). Maar je kunt ook bedenken dat punt P'(x';y') weer overgaat in punt P(x;y) bij een rotatie om de oorsprong over een hoek -θ, zodat we door verwisseling van (x;y) en (x';y') en met gebruik van de identiteiten cos(-θ) = cos θ en sin(-θ) = -sin θ uit (7a) en (7b) direct kunnen afleiden dat ook geldt:
(8a) x = x'∙cos θ + y'∙sin θ
(8b) y = -x'∙sin θ + y'∙cos θ
Je opmerking dat differentiatie van de cosinus en de sinus functies beantwoordt aan een rotatie over een rechte hoek tegen de klok in is overigens juist, zie ook hier.
E(X^2)=E(X)^2+V(X), en E(X)=0 en V(X)=t.quote:
Waarom is de verwachtingswaarde van een gekwadrateerd wiener proces gelijk aan t?
Soort van vervolgvraag hierop. Ik probeer nu deze op te lossen:quote:
[..]
Als ik je linkje doorlees, dan denk ik dat je D2u moet schrijven, niet D2x, want u is je afhankelijke variabele, niet x: Any character immediately following a differentiation operator is a dependent variable. En dan natuurlijk ook u(0) en u(L) schrijven. Overigens gaan dit soort dingen gemakkelijk in WolframAlpha.
http://www.wolframalpha.c(...)+0%2C+u%28L%29+%3D+0
Echter krijg ik weer de 0-oplossing. Slechts als ik 1 van de 2 randvoorwaarden toevoeg krijg ik een oplossing van de vorm waar ik naar op zoek ben, maar uiteraard wel verschillende oplossingen. Wat doe ik nu weer fout?
gr gr
Akkoord. Had ik. Waarom V(X)=t?quote:
[..]
E(X^2)=E(X)^2+V(X), en E(X)=0 en V(X)=t.
Wat gebruik je als definitie van je Wiener proces?quote:
[..]
Akkoord. Had ik. Waarom V(X)=t?
Ik ken de definitie dat W een Wiener proces is als (onder andere) W(t) - W(s) normaal verdeeld is met gemiddelde 0 en variantie t-s.
Je doet deze keer niets fout, maar het is hier zo dat je randvoorwaarden u(0) = 0 en u(L) = 0 maken dat u(x) = 0 inderdaad de (enige) oplossing is van je DV. Je kunt dit gemakkelijk inzien door als randvoorwaarden u(0) = 0 en u(L) = c te nemen (klik), dan zie je dat u(x) een functie is met een constante factor c, zodat de functie dus identiek gelijk wordt aan nul voor c = 0. Wellicht heb je dus je randvoorwaarden niet goed overgenomen van de oorspronkelijke opgave.quote:
[..]
Soort van vervolgvraag hierop. Ik probeer nu deze op te lossen:
http://www.wolframalpha.c(...)+0%2C+u%28L%29+%3D+0
Echter krijg ik weer de 0-oplossing. Slechts als ik 1 van de 2 randvoorwaarden toevoeg krijg ik een oplossing van de vorm waar ik naar op zoek ben, maar uiteraard wel verschillende oplossingen. Wat doe ik nu weer fout?
Ik heb een vraag over galois theory. Stel we hebben de volgende situatie.Stel L is een splitting field voor een polynoom f over K. Verder geldt dat E een subfield is van L dat tevens K bevat. Laat phi een K-monomorphism zijn van E into L. Waarom is L ook een splitting field voor f over E en phi(E)?
-
L is ook een splitting field van f over E, omdat je E nog met de resterende nulpunten van f uitbreidt tot L. Hetzelfde geldt volgens mij ook voor phi(E).quote:
Ik heb een vraag over galois theory. Stel we hebben de volgende situatie.Stel L is een splitting field voor een polynoom f over K. Verder geldt dat E een subfield is van L dat tevens K bevat. Laat phi een K-monomorphism zijn van E into L. Waarom is L ook een splitting field voor f over E en phi(E)?
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Je uitleg volg ik niet helemaal. Zou je dit kunnen verduidelijken met een voorbeeld? Speelt de monomorphism nog een rol?quote:
[..]
L is ook een splitting field van f over E, omdat je E nog met de resterende nulpunten van f uitbreidt tot L. Hetzelfde geldt volgens mij ook voor phi(E).
-
Bekijk f=(x^2+1)(x^2-2) met coëfficiënten inquote:
[..]
Je uitleg volg ik niet helemaal. Zou je dit kunnen verduidelijken met een voorbeeld? Speelt de monomorphism nog een rol?
Een K-monomorfisme stuurt alle elementen uit K naar K en de uitbreidingselementen worden injectief naar de uitbreidingselementen gestuurd. Dus phi(E) is dan gewoon E en phi(E_1) is dan of E of E_1 of E_2 of
[ Bericht 2% gewijzigd door Mathemaat op 18-12-2012 16:18:06 ]
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Wat voor vergelijking wil je maken met wat voor formule?quote:
Kan iemand mij eens vertellen hoe je een vergelijking moet maken bij een formule ?
Nee, dat kan niemand je vertellen als je niet wat meer bijzonderheden geeft, of een uitgewerkt voorbeeld van wat je bedoelt.quote:
Kan iemand mij eens vertellen hoe je een vergelijking moet maken bij een formule ?
quote:
[..]
Nee, dat kan niemand je vertellen als je niet wat meer bijzonderheden geeft, of een uitgewerkt voorbeeld van wat je bedoelt.
Sorry hier de opgavequote:
[..]
Wat voor vergelijking wil je maken met wat voor formule?
\
[ Bericht 1% gewijzigd door Beverwijker op 18-12-2012 19:37:15 (verkeerde afbeelding) ]
prijs = 12.75 + 8.95*tquote:
[..]
[..]
Sorry hier de opgave
\
[ afbeelding ]
prijs = 120.15
Kan je dit samenvatten in één vergelijking/formule (is hetzelfde)?
[quote] Op dinsdag 18 december 2012 19:39 schreef thenxero het volgende:
[..]
Op dinsdag 18 december 2012 19:39 schreef thenxero het volgende:[..]
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.edit: de verkeerde gequote zie ik nu
Noem de huurprijs in euro's uitgedrukt H en de tijdsduur uitgedrukt in dagen T, dan heb je dus:quote:
[..]
[..]
Sorry hier de opgave
\
[ afbeelding ]
(1) H = 12,75 + 8,95∙T
Nu is ook gegeven dat:
(2) H = 120,15
Uit (1) en (2) volgt dus:
(3) 12,75 + 8,95∙T = 120,15
Een lineaire vergelijking als deze oplossen met 'inklemmen' is flauwekul, dus daar doe ik niet aan. Als je van beide leden van (3) 12,75 aftrekt krijg je:
(4) 8,95∙T = 107,4
En beide leden van (4) delen door 8,95 geeft dan:
(5) T = 12
Inklemmen is inderdaad je reinste onzin; echter op vmbo behoort dit tot de reguliere stof. Dus er mogen m.i. best vragen over gesteld worden hier. Dit topic is er voor wiskunde vragen en niet alleen voor alleen voor de slimste FOK!kers.
kloep kloep
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Trouwens , Van mijn leraar hoeven wij niet in te klemmen hij heeft ons een trucje gegeven hoe je het ook kan doen .
Als we soms les hebben van een andere leraar dan moeten we het wel gebruiken dus het is wel altijd handig om te weten.
Als we soms les hebben van een andere leraar dan moeten we het wel gebruiken dus het is wel altijd handig om te weten.
Zo nu en dan is dat wel geinig om te zien in dit topic... staat er in de vraag 'los op met inklemmen' --> nee dat is flauwekul, zo gaan we het doen. Staat er in de vraag één klein detail verkeerd opgeschreven --> nee de vraag klopt niet en ik los hem ook niet op voor je.
Tja, je zult ongetwijfeld hebben gemerkt dat ik nogal eens compete uitwerkingen of afleidingen post, en dat doe ik niet zonder reden, ik hoop namelijk dat de vragenstellers, maar mogelijk ook andere meelezers die het nodig hebben, daar iets van opsteken. Een helder uitgewerkt vraagstuk kan dienen als model om te imiteren en zo soortgelijke vraagstukken zelf te leren oplossen. In oudere schoolboeken zie je dan ook dat alle stof compleet wordt uitgelegd en dat werkt het beste. Maar omdat dat in de huidige schoolboeken niet niet meer gebeurt en er kennelijk ook geen les meer wordt gegeven krijg je mensen die het zelfs aan de meest basale vaardigheden ontbreekt en die ook niet in staat zijn om een uitwerking helder en correct op te schrijven, en dat is niet goed.quote:
[..]
Misschien beter als je niet direct alles voordoet.
Heb je er wel eens over gedacht om een wiki te beginnen, en die te vullen met voorbeelden aan de hand van de antwoorden die je hier geeft? Dat je die wiki uitbreidt elke keer als er hier een vraag gesteld wordt?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
De doelgroep heeft waarschijnlijk toch geen zin om te zoeken. Als ze dat wel hadden, hadden ze al duizenden van dat soort wiki's gevonden.
Ja, maar daar gaat nog een hoop werk in zitten, net als in het (niet gerealiseerde) idee van Bram om lijsten te maken met linkjes naar vrij beschikbaar studiemateriaal per gebied van de wiskunde. Hij wilde daar een topic(reeks) van maken, maar ik heb toen gezegd dat een Wiki (binnen FOK) beter zou zijn omdat die zich beter leent om voortdurend te actualiseren en om het materiaal te ordenen, vooral als dat wat omvangrijker wordt. Maar ook daar gaat erg veel tijd in zitten. Mensen die oude posts van mij willen vinden moeten maar de zoekfunctie van FOK gebruiken, of anders Google, met de toevoeging site:.fok.nl achter de zoekopdracht.quote:
Heb je er wel eens over gedacht om een wiki te beginnen, en die te vullen met voorbeelden aan de hand van de antwoorden die je hier geeft? Dat je die wiki uitbreidt elke keer als er hier een vraag gesteld wordt?
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |