SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
[ Bericht 0% gewijzigd door GlowMouse op 22-05-2012 21:22:48 ]
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
[ Bericht 0% gewijzigd door GlowMouse op 22-05-2012 21:22:48 ]


dat hoef je niet te vermelden aangezien je ook op het pijltje naast de topictitel kunt klikkenquote:Op dinsdag 22 mei 2012 21:10 schreef Amoeba het volgende:
Vorig topic:
[Bèta wiskunde] Huiswerk- en vragentopic
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Thanks, dat wist ik niet. Nu je er toch bent: Ik wil graag weten hoe je die LaTeX code gebruikt, maar die URL werkt niet meer. Is er een handig tooltje om die 'integralen' en formules op te stellen? (Dus in een GUI vorm?)quote:Op dinsdag 22 mei 2012 21:11 schreef GlowMouse het volgende:
[..]
dat hoef je niet te vermelden aangezien je ook op het pijltje naast de topictitel kunt klikken


Je kunt de tex-tag gebruiken. Die werkt niet voor tekst, maar wel voor formules:
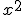
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


En hoe zet ik dan die integraal (van a tot b) op?quote:Op dinsdag 22 mei 2012 21:21 schreef GlowMouse het volgende:
Je kunt de tex-tag gebruiken. Die werkt niet voor tekst, maar wel voor formules:


Nou goed, dan gaan we verder met de functie:
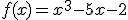
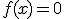
Dan krijgen we dus de vergelijking:
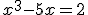
Ik had D al uitgerekend, dat was kleiner dan 0. In de spoiler even de toevoeging!
Dan krijgen we dus de vergelijking:
Ik had D al uitgerekend, dat was kleiner dan 0. In de spoiler even de toevoeging!
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Verder:
(substitutie)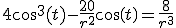
Gaan we r uitrekenen:
Dus r is bekend:
Wat moet ik hier nu mee.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
[ Bericht 26% gewijzigd door #ANONIEM op 22-05-2012 22:15:43 ]


quote:Op dinsdag 22 mei 2012 21:56 schreef Amoeba het volgende:
Nou goed, dan gaan we verder met de functie:
Dan krijgen we dus de vergelijking:
Ik had D al uitgerekend, dat was kleiner dan 0. In de spoiler even de toevoeging!SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Verder:
(substitutie)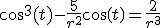
Gaan we r uitrekenen:
Dus r is bekend:
Wat moet ik hier nu mee.Edit: je vergeet inderdaad met 4 te vermenigvuldigen. Overigens zie je hier gemakkelijk dat x = -2 een oplossing is, dus kun je x3 - 5x - 2 door (x + 2) delen, en dat levert via een staartdeling x2 - 2x - 1 op, zodat de andere twee wortels dus 1 + √2 en 1 - √2 zijn. Controleer maar eens of je dat via de goniometrische methode ook vindt.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
[ Bericht 9% gewijzigd door Riparius op 22-05-2012 22:45:36 ]


Er zat wel een foutje in, had niet met vier vermenigvuldigd.
Ach, dan komt er een arccos antwoord uit.
En het ging me niet om het rekenwerk, maar om die [tex] opmaak.
Maargoed, het is begrepen. Ik had alle 3 exacte antwoorden wel getypt, maar die rot TEX kan niet overweg met dat tekentje, en ik had geen zin meer om het aan te passen.
[ Bericht 32% gewijzigd door #ANONIEM op 22-05-2012 22:35:17 ]
Ach, dan komt er een arccos antwoord uit.
En het ging me niet om het rekenwerk, maar om die [tex] opmaak.
Maargoed, het is begrepen. Ik had alle 3 exacte antwoorden wel getypt, maar die rot TEX kan niet overweg met dat tekentje, en ik had geen zin meer om het aan te passen.
[ Bericht 32% gewijzigd door #ANONIEM op 22-05-2012 22:35:17 ]


Ik gebruik zelf geen TeX, maar wel Unicode. Veel oude postings op FOK in het wiskunde topic zijn volkomen onleesbaar geworden omdat de server waarop TeX vroeger draaide niet meer werkt. En niemand kan garanderen dat dat niet weer gebeurt.quote:Op dinsdag 22 mei 2012 22:20 schreef Amoeba het volgende:
Er zat wel een foutje in, had niet met vier vermenigvuldigd.
Ach, dan komt er een arccos antwoord uit.
En het ging me niet om het rekenwerk, maar om die [tex] opmaak.
Maargoed, het is begrepen. Ik had alle 3 exacte antwoorden wel getypt, maar die rot TEX kan niet overweg met dat tekentje, en ik had geen zin meer om het aan te passen.


Welk tekentje bedoel je? Met TeX kun je vrijwel alles weergeven.quote:Op dinsdag 22 mei 2012 22:20 schreef Amoeba het volgende:
Er zat wel een foutje in, had niet met vier vermenigvuldigd.
Ach, dan komt er een arccos antwoord uit.
En het ging me niet om het rekenwerk, maar om die [tex] opmaak.
Maargoed, het is begrepen. Ik had alle 3 exacte antwoorden wel getypt, maar die rot TEX kan niet overweg met dat tekentje, en ik had geen zin meer om het aan te passen.
Ik zie nu overigens dat we via de goniometrische oplossing en de oplossing door te factoriseren tot de conclusie kunnen komen dat:
2∙√(5/3)∙cos((1/3)∙arccos((3/5)∙√(3/5))) = 1 + √2
Lijkt me wel een aardige uitdaging om dit via herleiding te bewijzen ...


pi in unicode. πquote:Op dinsdag 22 mei 2012 23:19 schreef Riparius het volgende:
[..]
Welk tekentje bedoel je? Met TeX kun je vrijwel alles weergeven.
Ik zie nu overigens dat we via de goniometrische oplossing en de oplossing door te factoriseren tot de conclusie kunnen komen dat:
2∙√(5/3)∙cos((1/3)∙arccos((3/5)∙√(3/5))) = 1 + √2
Lijkt me wel een aardige uitdaging om dit via herleiding te bewijzen ...
knip
Waarom precies deel je door (x+2) Als x=-2 komt er een duivelse breuk uit
En ik beheers geen staartdeling. Wel breuken uitdelen..
[ Bericht 5% gewijzigd door #ANONIEM op 22-05-2012 23:50:48 ]


Pi is in TeX gewoon \pi:quote:
The biggest argument against democracy is a five minute discussion with the average voter.


Nee hoor.quote:Op dinsdag 22 mei 2012 23:42 schreef Amoeba het volgende:
[..]
pi in unicode. π
knip
Waarom precies deel je door (x+2) Als x=-2 komt er een duivelse breuk uit
Dat blijkt. Heb je tóch nodig, gauw leren dus.quote:En ik beheers geen staartdeling.
Als x = -2 een nulpunt is van een polynoom in x, dan is dat polynoom deelbaar door (x + 2). Je hebt:
x3 - 5x - 2 = (x + 2)(x2 - 2x - 1)
Controleer maar door de haakjes uit te werken. De twee andere wortels zijn dus de wortels van de vierkantsvergelijking x2 - 2x - 1 = 0, zijnde 1 + √2 en 1 - √2.


Ik snapte er nog steeds geen zak van totdat ik de wiskundige regel zag. Helder. Ik heb m'n best gedaan om het te leren, maar met breuken uitdelen lukt het toch ook?quote:Op woensdag 23 mei 2012 00:06 schreef Riparius het volgende:
[..]
Nee hoor.
[..]
Dat blijkt. Heb je tóch nodig, gauw leren dus.
Als x = -2 een nulpunt is van een polynoom in x, dan is dat polynoom deelbaar door (x + 2). Je hebt:
x3 - 5x - 2 = (x + 2)(x2 - 2x - 1)
Controleer maar door de haakjes uit te werken. De twee andere wortels zijn dus de wortels van de vierkantsvergelijking x2 - 2x - 1 = 0, zijnde 1 + √2 en 1 - √2.


Kennelijk niet of niet zo goed, anders had je meteen gezien dat het klopte.quote:Op woensdag 23 mei 2012 00:13 schreef Amoeba het volgende:
[..]
Ik snapte er nog steeds geen zak van totdat ik de wiskundige regel zag. Helder. Ik heb m'n best gedaan om het te leren, maar met breuken uitdelen lukt het toch ook?


..quote:Op woensdag 23 mei 2012 00:18 schreef Riparius het volgende:
[..]
Kennelijk niet of niet zo goed, anders had je meteen gezien dat het klopte.
Ik zag niet dat je de functie aan het ombouwen was tot (...) = 0 v (......) = 0
En uiteraard ( x+2)(......) is de originele functie.
Enfin, ik ben er weg van. Wederom loopt over 4 uur de wekker af..


@Amoeba: aangezien Riparius al gezegd had dat x = -2 een oplossing is moet dus gelden dat de kubische vgl te schrijven is als een product van de lineaire factor (x+2) en een kwadratische factor (ax2 + bx + c)
Dus kunnen we gelijk met die (x+2) de polynoomstaartdeling uitwerken.
(x+2) | x3 - 5x - 2
....x2...| x3 + 2x2____-
...........|-2x2 -5x -2
..-2x....| -2x2-4x____-
...........|...........-x -2
...-1....|_____-x -2__-
.............................0
Wat dus uiteindelijk x3 - 5x - 2 = (x + 2)(x2 - 2x - 1) oplevert
Dus kunnen we gelijk met die (x+2) de polynoomstaartdeling uitwerken.
(x+2) | x3 - 5x - 2
....x2...| x3 + 2x2____-
...........|-2x2 -5x -2
..-2x....| -2x2-4x____-
...........|...........-x -2
...-1....|_____-x -2__-
.............................0
Wat dus uiteindelijk x3 - 5x - 2 = (x + 2)(x2 - 2x - 1) oplevert


Ik had het al door.quote:Op woensdag 23 mei 2012 03:11 schreef VanishedEntity het volgende:
@Amoeba: aangezien Riparius al gezegd had dat x = -2 een oplossing is moet dus gelden dat de kubische vgl te schrijven is als een product van de lineaire factor (x+2) en een kwadratische factor (ax2 + bx + c)
Dus kunnen we gelijk met die (x+2) de polynoomstaartdeling uitwerken.
(x+2) | x3 - 5x - 2
....x2...| x3 + 2x2____-
...........|-2x2 -5x -2
..-2x....| -2x2-4x____-
...........|...........-x -2
...-1....|_____-x -2__-
.............................0
Wat dus uiteindelijk x3 - 5x - 2 = (x + 2)(x2 - 2x - 1) oplevert


Vraagje hoe heet een curve die sterk lijkt op B.V. http://www.wolframalpha.com/input/?i=1-exp%28-x%29+from+0+to+3? Halve s-curve? Of heeft het geen naam?


In het Duits heet dit een Exponentielle Annäherungskurve, maar in het Nederlands (of in het Engels) is er dacht ik geen specifieke naam voor. Maar ja, in het Duits heeft zo ongeveer alles een naam. Zo is er bijvoorbeeld ook geen goed Engels equivalent voor Drehstreckung, zodat Engelse auteurs dan soms maar de Duitse term gebruiken. In dit laatste geval ligt de Nederlandse vertaling draaistrekking wel voor de hand, maar die term is nooit echt populair geworden.quote:Op donderdag 24 mei 2012 15:31 schreef Dale. het volgende:
Vraagje hoe heet een curve die sterk lijkt op B.V. http://www.wolframalpha.com/input/?i=1-exp%28-x%29+from+0+to+3? Halve s-curve? Of heeft het geen naam?


Oke thanks! Meende te herinneren dat er een woord voor was in het Engelsquote:Op donderdag 24 mei 2012 19:01 schreef Riparius het volgende:
[..]
In het Duits heet dit een Exponentielle Annäherungskurve, maar in het Nederlands (of in het Engels) is er dacht ik geen specifieke naam voor. Maar ja, in het Duits heeft zo ongeveer alles een naam. Zo is er bijvoorbeeld ook geen goed Engels equivalent voor Drehstreckung, zodat Engelse auteurs dan soms maar de Duitse term gebruiken. In dit laatste geval ligt de Nederlandse vertaling draaistrekking wel voor de hand, maar die term is nooit echt populair geworden.


Na een beetje googelen vind ik dat biologen en andere toegepaste wetenschappers wel de term asymptotic exponential curve gebruiken. Wiskundig onzinnig natuurlijk want andere exponentiële curves hebben evengoed een horizontale asymptoot, maar misschien is dat wat je zocht?quote:Op donderdag 24 mei 2012 20:34 schreef Dale. het volgende:
[..]
Oke thanks! Meende te herinneren dat er een woord voor was in het Engels


Toch maar in het gewone wiskundetopic, want daar past het het best denk ik.
Ik heb dit probleem:
Ik ben al flink bezig geweest met omschrijven, maar ik kom niet uit op de onderste formule voor tau. Ik snap niet waar die pi nou vandaan komt. Iemand die het wel doorheeft?
Ik heb dit probleem:
Ik ben al flink bezig geweest met omschrijven, maar ik kom niet uit op de onderste formule voor tau. Ik snap niet waar die pi nou vandaan komt. Iemand die het wel doorheeft?
gr gr


Lijkt me eenvoudig. Je hebt:quote:Op donderdag 24 mei 2012 23:18 schreef Quyxz_ het volgende:
Toch maar in het gewone wiskundetopic, want daar past het het best denk ik.
Ik heb dit probleem:
[ afbeelding ]
Ik ben al flink bezig geweest met omschrijven, maar ik kom niet uit op de onderste formule voor tau. Ik snap niet waar die pi nou vandaan komt. Iemand die het wel doorheeft?
F(x) + k∙x = 0,
dus:
m∙x''(t) + k∙x(t) = 0,
of:
x''(t) = -(k/m)∙x(t)
Dit is een tweede orde lineaire homogene differentiaalvergelijking. Los deze eens op de bekende manier op door te substitueren:
x(t) = eλt
[ Bericht 0% gewijzigd door Riparius op 26-05-2012 12:30:00 ]


Iemand toevallig van het programa Mathematica en state space models?
Blues ain't nothing but a good man feeling bad...


Dat kan ik doen, maar ik kom dan nog steeds niet uit op die vergelijking voor tau.quote:Op donderdag 24 mei 2012 23:34 schreef Riparius het volgende:
[..]
Lijkt me eenvoudig. Je hebt:
F(x) + k∙x = 0,
dus:
m∙x''(t) + k∙x(t) = 0,
of:
x''(t) = -(k/m)∙x(t)
Dit is een tweede orde lineaire homogene differentiaalvergelijking. Los deze eens op de bekende manier op door te substitueren:
x(t) = C∙eλt
En sowieso heb ik dan 4 onbekenden en maar 2 randvoorwaarden.
[ Bericht 4% gewijzigd door Quyxz_ op 25-05-2012 11:07:20 ]
gr gr


k en m worden als bekend beschouwd (je kan ze dus gewoon in je antwoord laten staan). Los eerst de differentiaalvergelijking eens op, zoals Riparius al suggereerde, en bedenk dan nog eens wat voor punt je precies zoekt.quote:Op vrijdag 25 mei 2012 11:01 schreef Quyxz_ het volgende:
[..]
Dat kan ik doen, maar ik kom dan nog steeds niet uit op die vergelijking voor tau.
En sowieso heb ik dan 4 onbekenden en maar 2 randvoorwaarden.


Ik heb het nu opgelost met een ietwat andere benadering. Geen idee of het geheel correct is, maar ik kom iig wel goed uit. Ik zal zo de berekening plaatsen.quote:Op vrijdag 25 mei 2012 11:31 schreef kutkloon7 het volgende:
[..]
k en m worden als bekend beschouwd (je kan ze dus gewoon in je antwoord laten staan). Los eerst de differentiaalvergelijking eens op, zoals Riparius al suggereerde, en bedenk dan nog eens wat voor punt je precies zoekt.
Edit: Dit is mijn berekening. Wat is er allemaal fout?
[ Bericht 13% gewijzigd door Quyxz_ op 25-05-2012 11:59:31 ]
gr gr


De oplossing die je uiteindelijk voor je differentiaalvergelijking vindt is goed, namelijk:quote:Op vrijdag 25 mei 2012 11:46 schreef Quyxz_ het volgende:
[..]
Ik heb het nu opgelost met een ietwat andere benadering. Geen idee of het geheel correct is, maar ik kom iig wel goed uit. Ik zal zo de berekening plaatsen.
Edit: Dit is mijn berekening. Wat is er allemaal fout?
[ afbeelding ]
x(t) = cos ωt,
met
ω = √(k/m)
Maar de manier waarop je dat opschrijft is niet correct. Je algemene oplossing is namelijk een lineaire combinatie niet van cos ωt en i∙sin ωt maar van eiωt en e-iωt. Uit
λ2 = -k/m
volgt immers (aangezien m en k positief zijn):
λ = i∙√(k/m) ∨ λ = -i∙√(k/m),
zodat:
x(t) = c1∙ei∙√(k/m)∙t + c2∙e-i∙√(k/m)∙t
de algemene oplossing is van de differentiaalvergelijking. Met behulp van de beginvoorwaarden x(0) = 1 en x'(0) = 0 vind je dan c1 + c2 = 1 en c1 - c2 = 0, zodat c1 = c2 = ½ en we dus krijgen:
x(t) = (ei∙√(k/m)∙t + e-i∙√(k/m)∙t)/2 = cos (√(k/m)∙t)
Hiervoor kunnen we schrijven x(t) = cos ωt met ω = √(k/m) waarbij ω (= 2πf) de cirkelfrequentie wordt genoemd. De periodeduur T (= 1/f) is nu het kleinste positieve getal zodanig dat voor elke t geldt:
x(t + T) = x(t)
Aangezien cos t een periode 2π heeft, heeft x(t) = cos ωt een periode
T = 2π/ω,
immers:
x(t + 2π/ω) = cos(ω(t + 2π/ω)) = cos(ωt + 2π) = cos ωt = x(t)
Verder had je al correct aangegeven dat:
τ = ¼T,
zodat we inderdaad krijgen:
τ = π/2ω
[ Bericht 0% gewijzigd door Riparius op 25-05-2012 23:07:16 ]


We hebben nu graaftheorie, maar ik vind die bewijsvragen behoorlijk lastig moet ik zeggen..
Zij D = (V, A) een gerichte graaf, en zij R een gesloten gerichte wandeling in
D. Bevat R een gerichte cykel? Zo ja, geef een bewijs. Zo nee, geef een
tegenvoorbeeld.
Een gerichte wandeling in een gerichte graaf van v0 naar vk is een rij v0,e1,v1,..,ek,vk van punten pijlen z.d.d ei een pijl is van vi-1 naar vi. Als de gerichte wandeling gesloten is dan is v0 gelijk aan vk. Dus R is een rij v0,e1,v1,..ek,v0.
Een gerichte cykel in een gerichte graaf is een gesloten gerichte wandeling waarin alle pijlen en alle punten (behalve begin- en eindpunt) verschillend zijn.
Ik denk zelf dat een gesloten gerichte wandeling R in een gerichte graaf D per definitie een gerichte cykel bevat met lengte kleiner dan of gelijk aan de lengte van R.
Alleen hoe bewijs ik zoiets nou perfect?
Zij D = (V, A) een gerichte graaf, en zij R een gesloten gerichte wandeling in
D. Bevat R een gerichte cykel? Zo ja, geef een bewijs. Zo nee, geef een
tegenvoorbeeld.
Een gerichte wandeling in een gerichte graaf van v0 naar vk is een rij v0,e1,v1,..,ek,vk van punten pijlen z.d.d ei een pijl is van vi-1 naar vi. Als de gerichte wandeling gesloten is dan is v0 gelijk aan vk. Dus R is een rij v0,e1,v1,..ek,v0.
Een gerichte cykel in een gerichte graaf is een gesloten gerichte wandeling waarin alle pijlen en alle punten (behalve begin- en eindpunt) verschillend zijn.
Ik denk zelf dat een gesloten gerichte wandeling R in een gerichte graaf D per definitie een gerichte cykel bevat met lengte kleiner dan of gelijk aan de lengte van R.
Alleen hoe bewijs ik zoiets nou perfect?


Ik heb niet zoveel verstand van graaftheorie, maar in de definitie van de gerichte cykel wordt nog extra geëist dat alle tussenliggende punten verschillend zijn.quote:Op dinsdag 29 mei 2012 22:56 schreef Physics het volgende:
We hebben nu graaftheorie, maar ik vind die bewijsvragen behoorlijk lastig moet ik zeggen..
Zij D = (V, A) een gerichte graaf, en zij R een gesloten gerichte wandeling in
D. Bevat R een gerichte cykel? Zo ja, geef een bewijs. Zo nee, geef een
tegenvoorbeeld.
Een gerichte wandeling in een gerichte graaf van v0 naar vk is een rij v0,e1,v1,..,ek,vk van punten pijlen z.d.d ei een pijl is van vi-1 naar vi. Als de gerichte wandeling gesloten is dan is v0 gelijk aan vk. Dus R is een rij v0,e1,v1,..ek,v0.
Een gerichte cykel in een gerichte graaf is een gesloten gerichte wandeling waarin alle pijlen en alle punten (behalve begin- en eindpunt) verschillend zijn.
Ik denk zelf dat een gesloten gerichte wandeling R in een gerichte graaf D per definitie een gerichte cykel bevat met lengte kleiner dan of gelijk aan de lengte van R.
Alleen hoe bewijs ik zoiets nou perfect?
Als je bijvoorbeeld de volgende graaf pakt:
(1) <--------> (2) <---------> (3)
Dan is R =[1,2,3,2,1] (met de juiste bijbehorende edges) een gesloten gerichte wandeling. Wordt er met 'R bevat een cykel' bedoeld dat er een deelrij is van R dat een een cykel vormt?
In dit geval is [1,2,1] een cykel bevat in R.
Het volgt in ieder geval niet direct uit de definitie.
[ Bericht 0% gewijzigd door thenxero op 29-05-2012 23:26:09 ]


Nog bedankt hiervoor trouwens.quote:Op vrijdag 25 mei 2012 15:34 schreef Riparius het volgende:
[..]
De oplossing die je uiteindelijk voor je differentiaalvergelijking vindt is goed, namelijk:
x(t) = cos ωt,
met
ω = √(k/m)
Maar de manier waarop je dat opschrijft is niet correct. Je algemene oplossing is namelijk een lineaire combinatie niet van cos ωt en i∙sin ωt maar van eiωt en e-iωt. Uit
λ2 = -k/m
volgt immers (aangezien m en k positief zijn):
λ = i∙√(k/m) ∨ λ = -i∙√(k/m),
zodat:
x(t) = c1∙ei∙√(k/m)∙t + c2∙e-i∙√(k/m)∙t
de algemene oplossing is van de differentiaalvergelijking. Met behulp van de beginvoorwaarden x(0) = 1 en x'(0) = 0 vind je dan c1 + c2 = 1 en c1 - c2 = 0, zodat c1 = c2 = ½ en we dus krijgen:
x(t) = (ei∙√(k/m)∙t + e-i∙√(k/m)∙t)/2 = cos (√(k/m)∙t)
Hiervoor kunnen we schrijven x(t) = cos ωt met ω = √(k/m) waarbij ω (= 2πf) de cirkelfrequentie wordt genoemd. De periodeduur T (= 1/f) is nu het kleinste positieve getal zodanig dat voor elke t geldt:
x(t + T) = x(t)
Aangezien cos t een periode 2π heeft, heeft x(t) = cos ωt een periode
T = 2π/ω,
immers:
x(t + 2π/ω) = cos(ω(t + 2π/ω)) = cos(ωt + 2π) = cos ωt = x(t)
Verder had je al correct aangegeven dat:
τ = ¼T,
zodat we inderdaad krijgen:
τ = π/2ω
gr gr


Het is ook een gerichte graaf, dus (1)<---->(2) is dan al niet mogelijk, alleen (1)-->(2) of (1)<--(2). Anders zou de stelling inderdaad niet gelden.quote:Op dinsdag 29 mei 2012 23:18 schreef thenxero het volgende:
[..]
Ik heb niet zoveel verstand van graaftheorie, maar in de definitie van de gerichte cykel wordt nog extra geëist dat alle tussenliggende punten verschillend zijn.
Als je bijvoorbeeld de volgende graaf pakt:
(1) <--------> (2) <---------> (3)
Dan is R =[1,2,3,2,1] (met de juiste bijbehorende edges) een gesloten gerichte wandeling. Wordt er met 'R bevat een cykel' bedoeld dat er een deelrij is van R dat een een cykel vormt?
In dit geval is [1,2,1] een cykel bevat in R.
Het volgt in ieder geval niet direct uit de definitie.


In een gerichte graaf mogen pijlen toch gewoon 2 kanten op getekend worden? 
En waarom geldt de stelling dan niet?
En waarom geldt de stelling dan niet?


Nee, in een gerichte graaf, heeft elke lijn tussen twee punten één richting. Als dat niet geld dan kan je een wandeling maken die heen en terug loopt tussen twee punten, dat is geen cykel.. (kan je met tegenvoorbeeld precies laten zien)quote:Op dinsdag 29 mei 2012 23:59 schreef thenxero het volgende:
In een gerichte graaf mogen pijlen toch gewoon 2 kanten op getekend worden?
En waarom geldt de stelling dan niet?
Wat ik zelf nu heb:
Zij R een gerichte wandeling v_0,v_1,...,_v_n dan zijn er gehele getallen i,k met i<k zodanig dat v_i=v_k. k is dan het kleinste geheel getal waarvoor dit geldt, dus k is de eerste v_k waarvoor v_i=v_k. Hieruit ontstaat dan de deelgraaf v_i,_v_i+1,...,v_k, dit is een gerichte cykel.


Ja maar je kan toch een lijn van a naar b tekenen en ook van b naar a? Anders hanteer je wel een aparte definitie van gerichte graaf. Je krijgt dan inderdaad wandelingen die geen cykel zijn.quote:Op woensdag 30 mei 2012 00:23 schreef Physics het volgende:
[..]
Nee, in een gerichte graaf, heeft elke lijn tussen twee punten één richting. Als dat niet geld dan kan je een wandeling maken die heen en terug loopt tussen twee punten, dat is geen cykel.. (kan je met tegenvoorbeeld precies laten zien)
Wat ik zelf nu heb:
Zij R een gerichte wandeling v_0,v_1,...,_v_n dan zijn er gehele getallen i,k met i<k zodanig dat v_i=v_k. k is dan het kleinste geheel getal waarvoor dit geldt, dus k is de eerste v_k waarvoor v_i=v_k. Hieruit ontstaat dan de deelgraaf v_i,_v_i+1,...,v_k, dit is een gerichte cykel.
R moet wel gesloten zijn natuurlijk.
Dus of dit correct is hangt volledig af van je definitie van gerichte grafen... controleer dat maar eens in je boek.


Ja klopt, hij moet wel gesloten zijn! Was ik even vergeten te typenquote:Op woensdag 30 mei 2012 00:33 schreef thenxero het volgende:
[..]
Ja maar je kan toch een lijn van a naar b tekenen en ook van b naar a? Anders hanteer je wel een aparte definitie van gerichte graaf. Je krijgt dan inderdaad wandelingen die geen cykel zijn.
R moet wel gesloten zijn natuurlijk.
Dus of dit correct is hangt volledig af van je definitie van gerichte grafen... controleer dat maar eens in je boek.
Volgens mij klopt het wel, mijn syllabus beschrijft de lijnen tussen punten in een gerichte graaf als één richting, die ofwel een inpijl danwel een uitpijl beschrijft.
Van wikipedia:
Dus hier zeggen dat ze een richting aanwijzen van de pijl, dus normaliter zijn (x,y) en (y,x) toegestaan, hier is alleen (x,y) of (y,x), afhankelijk van de richting.quote:An orientation of a simple undirected graph is obtained by assigning a direction to each edge


Waar zie je staan dat je niet (x,y) en (y,x) mag hebben als edges?
Of hoe noem je grafen waar je dan wel twee kanten op kan?
Of hoe noem je grafen waar je dan wel twee kanten op kan?


Grafen waar je wel twee kanten op kan zijn "undirected" ofwel gewone grafen. Directed is een extra eigenschap die je aan de lijnen/edges toevoegt.quote:Op woensdag 30 mei 2012 00:43 schreef thenxero het volgende:
Waar zie je staan dat je niet (x,y) en (y,x) mag hebben als edges?
Of hoe noem je grafen waar je dan wel twee kanten op kan?


Als je ionen moet benoemen he, en je hebt bijvoorbeeld Au³+, heet het dan gewoon goud-ion?
En klopt het ook dat Mn²+ het mangaan(II)-ion is?
En klopt het ook dat Mn²+ het mangaan(II)-ion is?


@wicky, dit is wiskunde he? Over de namen van de stoffen: kijk wat Fe is en wat N is. Staat allemaal keurig in de binas


Kaliumsulfide, ijzer(III)nitride en tin(tetra/IV)jodide?quote:Op woensdag 30 mei 2012 18:25 schreef Wicky15 het volgende:
Weet ook iemand wat de naam is van K2S, FeN en SnI4?
[ Bericht 0% gewijzigd door zoem op 30-05-2012 19:51:59 ]


Zat inderdaad verkeerd, sorry!quote:Op woensdag 30 mei 2012 18:54 schreef Don_Vanelli het volgende:
@wicky, dit is wiskunde he? Over de namen van de stoffen: kijk wat Fe is en wat N is. Staat allemaal keurig in de binas
Bedankt!quote:Op woensdag 30 mei 2012 19:13 schreef zoem het volgende:
[..]
Kaliumsulfide, ijzernitride en tin(tetra/IV)jodide?


Ik heb een vraag over conflictlijnen. Als je twee hoeken hebt die dezelfde kant op staan (dus: < <), is dan de middelloodlijn die op de bissectrice van de buitenste hoek ligt de conflictlijn? (Ik weet niet of het nou goed beschrijf, maar ik denk het wel...)


Ik ben tegen het gebruik van de term conflictlijn (zie ook hier) omdat het een term is waarbij allerlei verschillende meetkundige begrippen op één hoop worden gegooid, wat het inzicht niet ten goede komt en daarmee didactisch helemaal fout is. De term wordt kennelijk ook alleen maar in Nederland gehanteerd (hoe typisch). Maar afgezien daarvan is je vraagstelling onduidelijk. Probeer een plaatje te maken dat je vraagstelling illustreert.quote:Op vrijdag 1 juni 2012 16:40 schreef Aardappel2610 het volgende:
Ik heb een vraag over conflictlijnen. Als je twee hoeken hebt die dezelfde kant op staan (dus: < <), is dan de middelloodlijn die op de bissectrice van de buitenste hoek ligt de conflictlijn? (Ik weet niet of het nou goed beschrijf, maar ik denk het wel...)


En zulke grafen dan?quote:Op woensdag 30 mei 2012 00:46 schreef Physics het volgende:
[..]
Grafen waar je wel twee kanten op kan zijn "undirected" ofwel gewone grafen. Directed is een extra eigenschap die je aan de lijnen/edges toevoegt.
(1) < --- > (2) ---> (3)


In het Engels is er ook een woord voorquote:Op vrijdag 1 juni 2012 17:14 schreef Riparius het volgende:
[..]
De term wordt kennelijk ook alleen maar in Nederland gehanteerd (hoe typisch).
http://en.wikipedia.org/wiki/Locus_(mathematics)


Nee, locus is de Engelse term voor wat vooral vroeger in het Nederlands een meetkundige plaats werd genoemd. Dat is een begrip uit de klassieke Euclidische meetkunde, in tegenstelling tot het modebegrip conflictlijn. Een ellips of een hyperbool bijvoorbeeld wordt als een meetkundige plaats gedefinieerd, niet als een conflictlijn. Het hele begrip conflictlijn is overbodig en schept alleen maar verwarring.quote:Op vrijdag 1 juni 2012 17:55 schreef twaalf het volgende:
[..]
In het Engels is er ook een woord voor
http://en.wikipedia.org/wiki/Locus_(mathematics)
[ Bericht 0% gewijzigd door Riparius op 01-06-2012 22:06:43 ]


In het bericht waar je naar verwees staat dat een parabool wel een conflictlijn is. Waarom kun je hyperbool en ellips dan geen conflictlijn noemen?


Die heb ik nog ziet langskomen eigenlijk, volgens mij is dat niet gedefinieerd (maar durf ik niet met zekerheid te zeggen)?quote:Op vrijdag 1 juni 2012 17:30 schreef thenxero het volgende:
[..]
En zulke grafen dan?
(1) < --- > (2) ---> (3)


thenxero heeft gelijk, een directed graaf kan best arcs (a,b) en (b,a) hebben.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Omdat een ellips en een hyperbool niet worden gedefinieerd als een verzameling punten met gelijke afstanden tot twee andere punten of puntverzamelingen. Hetzelfde geldt uiteraard voor de cirkel.quote:Op vrijdag 1 juni 2012 18:26 schreef twaalf het volgende:
In het bericht waar je naar verwees staat dat een parabool wel een conflictlijn is. Waarom kun je hyperbool en ellips dan geen conflictlijn noemen?
Het begrip meetkundige plaats is veel algemener, het gaat daarbij om een verzameling van alle punten in het vlak die aan een bepaalde voorwaarde voldoen, en dat kan van alles zijn. Zo is bij twee gegeven punten A en B de meetkundige plaats van de punten P zodanig dat ∠APB recht is een cirkel met middellijn AB uitgezonderd de punten A en B zelf, maar dit is uiteraard geen conflictlijn.


Hihihi jij volgt het vak numerieke analyse op de TU/equote:Op donderdag 24 mei 2012 23:18 schreef Quyxz_ het volgende:
Toch maar in het gewone wiskundetopic, want daar past het het best denk ik.
Ik heb dit probleem:
[ afbeelding ]
Ik ben al flink bezig geweest met omschrijven, maar ik kom niet uit op de onderste formule voor tau. Ik snap niet waar die pi nou vandaan komt. Iemand die het wel doorheeft?


Dit is gecompliceerder dan je denkt. Aangenomen dat de beide hoeken recht zijn en de afstand van elk van de benen van hoek 1 tot de parallelle benen van hoek 2 gelijk is, is je conflictlijn binnen het vierkant dat wordt gevormd door de hoekpunten van beide hoeken en de voetpunten van de loodlijnen van het hoekpunt van hoek 1 op de benen van hoek 2 geen recht lijnstuk maar een paraboolsegment.quote:Op vrijdag 1 juni 2012 18:31 schreef Aardappel2610 het volgende:
[ afbeelding ]
Het gaat om de ruimte tussen 1 en 2.


Ik vermoedde al dat er iets met een parabool gedaan moest worden... Maar ergens lijkt dat heel onlogisch.
Ik heb het nu even uitgetekend en het resultaat is een kromme lijn in het hoekpunt. Als ik het goed begrijp moet zo'n hoek dus behandeld worden als een punt, i.p.v. twee lijnen die elkaar raken?
Ik heb het nu even uitgetekend en het resultaat is een kromme lijn in het hoekpunt. Als ik het goed begrijp moet zo'n hoek dus behandeld worden als een punt, i.p.v. twee lijnen die elkaar raken?


Nee, er is niets onlogisch aan. Zodra je binnen het genoemde vierkant zit, geldt dat de minimale afstand tot hoek 1 altijd gelijk is aan de afstand tot het hoekpunt van hoek 1, immers alle andere punten op de beide benen van hoek 1 liggen dan verder weg. Voor de minimale afstand tot hoek 2 geldt binnen het genoemde vierkant dat je de lengte van de kortste van de twee loodlijnen op elk van de benen van hoek 2 moet nemen als 'de' kortste afstand tot hoek 2.quote:Op vrijdag 1 juni 2012 19:07 schreef Aardappel2610 het volgende:
Ik vermoedde al dat er iets met een parabool gedaan moest worden... Maar ergens lijkt dat heel onlogisch.
Nee. Ik begrijp trouwens niet wat je hiermee precies bedoelt. Je moet de definitie van de conflictlijn hanteren. Maar zoals je zelf ziet leidt dat al gauw tot verwarringen.quote:Ik heb het nu even uitgetekend en het resultaat is een kromme lijn in het hoekpunt. Als ik het goed begrijp moet zo'n hoek dus behandeld worden als een punt, i.p.v. twee lijnen die elkaar raken?


Wel.quote:Op vrijdag 1 juni 2012 18:37 schreef Riparius het volgende:
[..]
Omdat een ellips en een hyperbool niet worden gedefinieerd als een verzameling punten met gelijke afstanden tot twee andere punten of puntverzamelingen.


Ken je de definities van een een ellips of een hyperbool als meetkundige plaats aan de hand van twee brandpunten F1 en F2 of aan de hand van één brandpunt F en een richtlijn d (directrix) wel?quote:


De verzameling van alle punten met gelijke afstand tot een vast punt en een vaste cirkel heet een ellips als het punt binnen de cirkel ligt en een hyperbool als het punt buiten de cirkel ligt. In die zin zie ik niet waarom ellips en hyperbool geen conflictlijnen zijn en de parabool wel. Ik ken ook de definitie met brandpunten, maar die doet er hier niet toe.quote:Op vrijdag 1 juni 2012 20:26 schreef Riparius het volgende:
[..]
Ken je de definities van een een ellips of een hyperbool als meetkundige plaats aan de hand van twee brandpunten F1 en F2 of aan de hand van één brandpunt F en een richtlijn d (directrix) wel?


Ja, zo kunnen ellips en hyperbool conflictlijnen zijn, maar zo worden ze niet gedefinieerd.quote:Op vrijdag 1 juni 2012 20:32 schreef twaalf het volgende:
[..]
De verzameling van alle punten met gelijke afstand tot een vast punt en een vaste cirkel heet een ellips als het punt binnen de cirkel ligt en een hyperbool als het punt buiten de cirkel ligt. In die zin zie ik niet waarom ellips en hyperbool geen conflictlijnen zijn en de parabool wel. Ik ken ook de definitie met brandpunten, maar die doet er hier niet toe.
Ik ken tenminste geen (leer)boeken waarin dit zo wordt gedaan.


Nee, er is niets zwaks aan mijn argumenten. Het lijkt erop alsof jij geen scherp onderscheid wenst te maken tussen definities en stellingen, terwijl dat onderscheid toch wezenlijk is voor de gehele wiskunde.quote:Op vrijdag 1 juni 2012 22:24 schreef twaalf het volgende:
Zwak argument, linksom of rechtsom is het een conflictlijn.
Een parabool kunnen we definiëren als de meetkundige plaats van punten in een plat vlak die op gelijke afstanden liggen van een lijn in dat vlak en een punt in dat vlak buiten die lijn. En deze definitie kunnen we inderdaad herformuleren in termen van een conflictlijn: een parabool is dan te (her)definiëren als een conflictlijn van een rechte en een punt buiten die rechte.
Maar de meetkundige definities van een ellips of een hyperbool, ongeacht of we deze definiëren aan de hand van twee vaste punten (de brandpunten of foci) of aan de hand van één vast punt (brandpunt of focus) en een rechte (richtlijn of directrix) zijn niet te herformuleren in termen van een conflictlijn gerelateerd aan de twee gegeven punten resp. het gegeven punt en de gegeven lijn. Dit brengt meteen ook de nutteloosheid van het begrip conflictlijn aan het licht: elke conflictlijn is een meetkundige plaats (locus), maar niet elke meetkundige plaats is een conflictlijn. We hebben dus voldoende aan het begrip meetkundige plaats, zoals dat al meer dan twee millennia wordt gebruikt in de euclidische meetkunde. Het begrip conflictlijn wordt sinds een jaar of vijftien gepropageerd door het Freudenthalinstituut, maar daar komen wel meer onzinnige ideeën vandaan t.a.v. de hervorming van het Nederlandse wiskunde-onderwijs. Het is ook een teken aan de wand dat het begrip conflictlijn verder nergens buiten Nederland wordt gebruikt, ook niet in Vlaanderen.
Nu kun je beweren dat de conflictlijn van een cirkel en een punt binnen die cirkel een ellips is, maar dat is dan geen definitie van een ellips, maar een stelling. En een stelling behoeft een bewijs, zie bijvoorbeeld hier.


Twaalf bedoelt denk ik dat je een ellips kan definiëren als de conflictlijn tussen een punt en een cirkel als het punt in de cirkel ligt. Met die definitie werkte ik ook op de middelbare school.
Staat ook zo in je bestandje:
Staat ook zo in je bestandje:
Ik zie het probleem niet.quote:De conflictlijn E van een punt P en de cirkel K heet een ellips


Ja, ik begrijp dat dat kan, als je twee equivalente definities A en B hebt dan kun je A of B kiezen als 'de' definitie, en de andere definitie tot een stelling maken door de equivalentie te bewijzen. Dick Klingens zit een beetje te schipperen in het PDFje waarnaar ik hierboven link, want hij zegt eerst (p. 6) "De conflictlijn E van het punt P en de cirkel K heet ellips" (mijn cursivering, Riparius), waarmee hij dus een definitie suggereert, maar even later geeft hij dan de bekende definitie van de ellips als meetkundige plaats van de punten waarvan de som van de afstanden tot twee vaste punten constant is. Maar goed, Klingens zit een beetje tussen twee vuren in als docent van de oude stempel en als lid van adviescommissies voor de vernieuwing van het wiskunde-onderwijs en dat verklaart wel waarom hij het zo doet.quote:Op zondag 3 juni 2012 17:26 schreef thenxero het volgende:
Twaalf bedoelt denk ik dat je een ellips kan definiëren als de conflictlijn tussen een punt en een cirkel als het punt in de cirkel ligt. Met die definitie werkte ik ook op de middelbare school.
[ Bericht 0% gewijzigd door Riparius op 03-06-2012 18:08:48 ]
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |



