SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Check haar filmpjesquote:Op woensdag 14 maart 2012 22:14 schreef bloodysunday het volgende:
[..]
Les gehad, werd ik niet veel wijzer van. Heb een boek, maar dat staat vol fouten dus dat schiet lekker op


Je droomt er zeker van dat ze jou het squeeze theorem nog eens persoonlijk komt uitleggen?quote:


Mwa, ik zou het in ieder geval niet weigeren.quote:Op woensdag 14 maart 2012 22:51 schreef Riparius het volgende:
[..]
Je droomt er zeker van dat ze jou het squeeze theorem nog eens persoonlijk komt uitleggen?


Toegepaste Wiskunde voor het Hoger Onderwijs.quote:Op woensdag 14 maart 2012 22:20 schreef Riparius het volgende:
[..]
Welk boek is dat, als ik vragen mag?
Je kunt natuurlijk zelf op zoek gaan naar een beter leerboek. Of kijk eens in Wikipedia.
AJAX AMSTERDAM!


Op een tentamen stond een keer de volgende vraag:
Je hebt 90 meter hekwerk. Het hek moet aan 1 zijde open zijn. Bepaal de maximale oppervlakte.
Wat voor formule moet je hier bij opzetten.
De oppervlakte is lxb maar aangezien je 1 zijde minder hebt moet het (lxb)-l zijn ofzo?
Je hebt 90 meter hekwerk. Het hek moet aan 1 zijde open zijn. Bepaal de maximale oppervlakte.
Wat voor formule moet je hier bij opzetten.
De oppervlakte is lxb maar aangezien je 1 zijde minder hebt moet het (lxb)-l zijn ofzo?
AJAX AMSTERDAM!


duidelijke vraagstelling!quote:Op donderdag 15 maart 2012 10:31 schreef bloodysunday het volgende:
Op een tentamen stond een keer de volgende vraag:
Je hebt 90 meter hekwerk. Het hek moet aan 1 zijde open zijn. Bepaal de maximale oppervlakte.
Wat voor formule moet je hier bij opzetten.
De oppervlakte is lxb maar aangezien je 1 zijde minder hebt moet het (lxb)-l zijn ofzo?


Wat jij doet kan niet; je trekt een lengte van een oppervlakte af. Let op je dimensiesquote:Op donderdag 15 maart 2012 10:31 schreef bloodysunday het volgende:
Op een tentamen stond een keer de volgende vraag:
Je hebt 90 meter hekwerk. Het hek moet aan 1 zijde open zijn. Bepaal de maximale oppervlakte.
Wat voor formule moet je hier bij opzetten.
De oppervlakte is lxb maar aangezien je 1 zijde minder hebt moet het (lxb)-l zijn ofzo?
Stel eerst de formule voor de oppervlakte op. Aangenomen dat het een rechthoekig vlak is, kun je het volgende zeggen: De rechthoek heeft vier zijdes, waarvan er eentje open is. De twee zijdes die grenzen aan de opening noem je
Het maximum vind je door de eerste afgeleide naar
[edit]
Inderdaad, ik ben vergeten het uiteindelijke antwoord te geven.
Hoezo is het niet duidelijk? Het enige wat niet expliciet gegeven is, is dat het een rechthoek moet zijn.quote:
[ Bericht 12% gewijzigd door zoem op 15-03-2012 15:02:31 ]


Inderdaad. Maar de vragensteller citeert de opgave kennelijk uit het hoofd, bij de oorspronkelijke opgave zal er wel bij hebben gestaan dat het ging om een rechthoekig terrein. Vaak was dat dan een terrein dat langs het water lag of zo.quote:Op donderdag 15 maart 2012 10:52 schreef zoem het volgende:
[..]
Hoezo is het niet duidelijk? Het enige wat niet expliciet gegeven is, is dat het een rechthoek moet zijn.
Je moet trouwens nog wel even het gevraagde antwoord geven: de maximaal af te rasteren oppervlakte bedraagt 1012,5 m². Vroeger waren dit gewone algebra opgaven die je geacht werd zonder differentiaalrekening op te kunnen lossen. De uitdrukking voor de oppervlakte is middels kwadraatafsplitsing te schrijven als A = 1012,5 - 2(x - 22,5)² zodat direct duidelijk is dat het maximum van 1012,5 m² bereikt wordt bij x = 22,5 m aangezien het kwadraat hier niet negatief kan zijn.


Dat kan ik me niet voorstellen, tenzij het een hele slechte docent was. Want stel dat we het hek in een halve cirkel plaatsen, of dat we het hek twee zijden van een gelijkzijdige driehoek laten vormen, of de twee rechthoekszijden van een rechthoekige driehoek, dan kun je zonder nadere gegevens net zo goed volhouden dat het hek 'aan één zijde open' is.quote:Op donderdag 15 maart 2012 18:30 schreef bloodysunday het volgende:
Nee dit was een zo'n beetje de vraag.


Ik heb een vraag over kansrekenen:
Een gezamenlijke kansdichtheid:
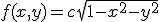
normaliseren geeft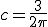
Nu zoek ik de marginale kansdichtheden.
Ik zag dit als plakjes snijden uit de bol, en wilde dan de oppervlakte van die plakjes bepalen. Alleen is f(x,y) geen echte bol. Hoe kan ik dit nu aanpakken?
Voor de andere vragen gebruikte ik poolcoordinaten om te integreren, maar ik weet niet of je daar de marginale kansdichtheden uit kon halen.
Een gezamenlijke kansdichtheid:
normaliseren geeft
Nu zoek ik de marginale kansdichtheden.
Ik zag dit als plakjes snijden uit de bol, en wilde dan de oppervlakte van die plakjes bepalen. Alleen is f(x,y) geen echte bol. Hoe kan ik dit nu aanpakken?
Voor de andere vragen gebruikte ik poolcoordinaten om te integreren, maar ik weet niet of je daar de marginale kansdichtheden uit kon halen.


Het is een ellips(oïde), de oppervlakte van een 'plakje' wordt gegeven door 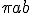 , waarin a en b de halve assen zijn. Voor gegeven x kun je a en b uitrekenen.
, waarin a en b de halve assen zijn. Voor gegeven x kun je a en b uitrekenen.


quote:Op zaterdag 17 maart 2012 23:29 schreef twaalf het volgende:
Het is een ellips(oïde), de oppervlakte van een 'plakje' wordt gegeven door, waarin a en b de halve assen zijn. Voor gegeven x kun je a en b uitrekenen.
Het is toch gewoon een bol?
Sorry je hebt gelijk, die c gooit roet in het eten.


Het is gelukt. Je kon ook uitgaan van een bol en dan normaliseren, maar nu snap ik het beter. Bedankt.


pi *a*b reduceert gewoon tot pi*r^2 (de bol wordt in de richting van de z-as uitgerekt door c)quote:Op zaterdag 17 maart 2012 23:58 schreef thabit het volgende:
Maakt het überhaupt iets uit dat daar een c staat? Het is toch alleen maar een schalingsfactor?


Weet iemand hoe je T=27•0,4^t•(3-0,4^2t) herleidt tot de vorm T=a•g^t+b•h^t ?
"Nibnub. A name to remember."


Wat je dan nog kan schrijven als:quote:Op zondag 18 maart 2012 12:18 schreef Anoonumos het volgende:
Dus eerst de haakjes uitwerken en dan gebruiken dat
Gebruikmakende van
[ Bericht 0% gewijzigd door Nelis89 op 18-03-2012 14:36:38 ]
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]


Fixedquote:Op zondag 18 maart 2012 14:33 schreef Riparius het volgende:
[..]
Het antwoord van Nelis89 klopt niet, want 0,43 = 0,064.
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]


Ik ben mijn wiskunde aan het oppoetsen en me langzaam door een dik wiskunde boek aan het werken.
Ik kom echter bij het volgende voorbeeld niet verder:
Maar daarna wordt me het spoor bijster. Waar komt die "+ 2k + 1" vandaan, en waar komt daarna de "+ 1 + (2k - 6)" vandaan?
Ik begrijp waarom de uitdrukking altijd waar is voor elke n ≥ 8, ik volg alleen de redenering en de inductie niet.
Als dit niet de juiste plek is voor mijn vraag, dan hoor ik het wel!

Ik kom echter bij het volgende voorbeeld niet verder:
Ik kan het nog net volgen tot: (k + 1)2 = k2 + 2k + 1 > ....quote:Bewijs dat n2 > 7n + 1 for alle n >= 8
Oplossing: Het resultaat is waar wanneer n = 8, want 82 = 64 en 7 * 8 + 1 = 57. Veronderstel dat het waar is voor iedere n wanneer k ≥ 8, dat wil zeggen k2 > 7k + 1
(k + 1)2 = k2 + 2k + 1 > (7k + 1) + 2k + 1 = 7(k + 1) + 1 + (2k - 6)
Omdat k ≥ 8, is 2k - 6 een natuurlijk nummer, en de laatste uitdrukking boven is groter dan 7(k + 1). De inductie stap is geverifiëerd, en dus is het resultaat waar voor alle n ≥ 8.
(vrij vertaald uit het Engels uit Discrete Mathematics van Normal L. Biggs)
Maar daarna wordt me het spoor bijster. Waar komt die "+ 2k + 1" vandaan, en waar komt daarna de "+ 1 + (2k - 6)" vandaan?
Ik begrijp waarom de uitdrukking altijd waar is voor elke n ≥ 8, ik volg alleen de redenering en de inductie niet.
Als dit niet de juiste plek is voor mijn vraag, dan hoor ik het wel!


Uit de kut van tante Sjaan!quote:Op maandag 19 maart 2012 21:28 schreef RedVampire het volgende:
Ik ben mijn wiskunde aan het oppoetsen en me langzaam door een dik wiskunde boek aan het werken.
Ik kom echter bij het volgende voorbeeld niet verder:
[..]
Ik kan het nog net volgen tot: (k + 1)2 = k2 + 2k + 1 > ....
Maar daarna wordt me het spoor bijster. Waar komt die "+ 2k + 1" vandaan, en waar komt daarna de "+ 1 + (2k - 6)" vandaan?
Je gebruikt hier k2 > 7k + 1; dat mag je doen omdat dat de inductiehypothese is.


Ik heb het een beetje herschreven en verduidelijkt:
quote:Bewijs dat n² > 7n + 1 for alle n >= 8
Oplossing: Het resultaat is waar wanneer n = 8, want 82 = 64 en 7 * 8 + 1 = 57. Veronderstel dat het waar is voor een k ≥ 8, dat wil zeggen k² > 7k + 1. (Hiermee willen we aantonen dat het ook geldt voor k+1). Dan
(k + 1)² = k² + 2k + 1
> (7k + 1) + 2k + 1 (vanwege de inductiehypothese: k² > 7k + 1)
= 7(k + 1) + 1 + (2k - 6) (herschrijven)
Omdat k ≥ 8, is 2k - 6>0, dus de laatste uitdrukking boven is groter dan 7(k + 1). De inductie stap is geverifiëerd, en dus is het resultaat waar voor alle n ≥ 8.
(vrij vertaald uit het Engels uit Discrete Mathematics van Normal L. Biggs)


Dus als ik het goed begrijpt, volg je de volgende stappen:quote:Op maandag 19 maart 2012 22:24 schreef thenxero het volgende:
Ik heb het een beetje herschreven en verduidelijkt:
[..]
1. schrijf de (k + 1)2 uit
2. voeg het verschil tussen k2 en (k + 1)2 bij 7k + 1
3. herschrijf je die functie naar het format 7(k + 1) + 1 + ...
De volgende stap snap ik nog steeds niet helemaal, want als k = 8, dan is 2k - 6 toch 10? En (2k - 6) is toch al groter dan 0 vanaf k = 4?


En dus ook vanaf k = 8.quote:Op maandag 19 maart 2012 22:57 schreef RedVampire het volgende:
[..]
De volgende stap snap ik nog steeds niet helemaal, want als k = 8, dan is 2k - 6 toch 10? En (2k - 6) is toch al groter dan 0 vanaf k = 4?


Wat je met stap 2 bedoelt is nogal vaag. Ik heb het idee dat je inductie nog niet helemaal snapt.quote:Op maandag 19 maart 2012 22:57 schreef RedVampire het volgende:
[..]
Dus als ik het goed begrijpt, volg je de volgende stappen:
1. schrijf de (k + 1)2 uit
2. voeg het verschil tussen k2 en (k + 1)2 bij 7k + 1
3. herschrijf je die functie naar het format 7(k + 1) + 1 + ...
De volgende stap snap ik nog steeds niet helemaal, want als k = 8, dan is 2k - 6 toch 10? En (2k - 6) is toch al groter dan 0 vanaf k = 4?
Het idee van inductie is dat je een uitspraak P bewijst vanaf een 'basis' (in dit geval n=8). Dan stel je dat dat P(k) waar is (dat heet de inductiehypothese), en dan laat je zien dat P(k+1) waar is. Als dat lukt, dan heb je bewezen dat het waar is voor iedere n groter dan de basis. Want uit het geval n=8 volgt het voor n=9, daaruit weer voor n=10, etc, als een soort domino-effect.
In dit specifieke neem je voor P(n) de uitspraak n² > 7n + 1. Dan bewijs je P(8), en stel je dat P(k) : k² > 7k + 1waar is (dat is je inductiehypothese). Je wil laten zien dat P(k+1) ook waar is, oftewel (k+1)² > 7(k+1) + 1. Dat doe je door (k+1)² uit te werken, je inductiehypothese te gebruiken, en te herschrijven. Dan zie je dat inderdaad (k + 1)² > 7(k + 1) + 1 + (2k - 6) > 7(k+1)+1, omdat (2k-6)>0 voor k>8. We bekijken k>8, omdat we het willen bewijzen voor k >= 8 (en k=8 is al bewezen). Dat het ook al geldt vanaf k=4 is fijn, maar dat heb je niet eens nodig.


Je hebt gelijk, ik heb inderdaad wat moeite met het concept. Ik snapte het met de voorgaande voorbeelden wel, die begonnen met sommatie waar dan een functie voor was gegeven en die je dan voor k=1 en k=k+1 moest bewijzen dat die functie de sommatie correct beschreef.quote:Op maandag 19 maart 2012 23:44 schreef thenxero het volgende:
[..]
Wat je met stap 2 bedoelt is nogal vaag. Ik heb het idee dat je inductie nog niet helemaal snapt.
Het idee van inductie is dat je een uitspraak P bewijst vanaf een 'basis' (in dit geval n=8). Dan stel je dat dat P(k) waar is (dat heet de inductiehypothese), en dan laat je zien dat P(k+1) waar is. Als dat lukt, dan heb je bewezen dat het waar is voor iedere n groter dan de basis. Want uit het geval n=8 volgt het voor n=9, daaruit weer voor n=10, etc, als een soort domino-effect.
In dit specifieke neem je voor P(n) de uitspraak n² > 7n + 1. Dan bewijs je P(8), en stel je dat P(k) : k² > 7k + 1waar is (dat is je inductiehypothese). Je wil laten zien dat P(k+1) ook waar is, oftewel (k+1)² > 7(k+1) + 1. Dat doe je door (k+1)² uit te werken, je inductiehypothese te gebruiken, en te herschrijven. Dan zie je dat inderdaad (k + 1)² > 7(k + 1) + 1 + (2k - 6) > 7(k+1)+1, omdat (2k-6)>0 voor k>8. We bekijken k>8, omdat we het willen bewijzen voor k >= 8 (en k=8 is al bewezen). Dat het ook al geldt vanaf k=4 is fijn, maar dat heb je niet eens nodig.
Maar begrijp ik je nu goed dat de eerste stap in de inductie heeft bewezen waar het punt ligt dat k2 groter wordt dan 7k + 1, en dat de k+1 stap in deze heeft bewezen dat de k2 tegenover 7k + 1 alsmaar groter wordt?


Nee, niet helemaal. Je hebt niet bewezen dat n=8 het kleinste getal is waar de uitspraak waar wordt (maar dat is natuurlijk wel eenvoudig na te gaan door n=7 in te vullen en te concluderen dat de uitspraak onwaar wordt). Je hebt wel al bewezen dat de uitspraak waar is vanaf n=8.quote:Op dinsdag 20 maart 2012 00:07 schreef RedVampire het volgende:
[..]
Je hebt gelijk, ik heb inderdaad wat moeite met het concept. Ik snapte het met de voorgaande voorbeelden wel, die begonnen met sommatie waar dan een functie voor was gegeven en die je dan voor k=1 en k=k+1 moest bewijzen dat die functie de sommatie correct beschreef.
Maar begrijp ik je nu goed dat de eerste stap in de inductie heeft bewezen waar het punt ligt dat k2 groter wordt dan 7k + 1
Probeer dit eens helder te formuleren.quote:en dat de k+1 stap in deze heeft bewezen dat de k2 tegenover 7k + 1 alsmaar groter wordt?


 Op
Op