SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Hee, dat is precies dezelfde opdracht als een die ik moest doenquote:Op dinsdag 11 oktober 2011 14:46 schreef bezemsteeltaart het volgende:
Hoe bereken ik de inverse van N=2^(5-3L)
Dus L=...N
ik weet dat ik ln/e moet gebruiken maar ik kom er niet echt uit, een voorzet is ook goed. BVD
Doe je ook het oefententamen bij Wiskunde 1 op de Eur? Nog bedankt voor het helpen, op het moment dat ik mijn vraag enkele posts hier boven stelde schoot het me te binnen, het is best wel simpel eigenlijk..
jep snuf, vindt jij het goed te doen? ik heb A gehad en heb er redelijk moeite mee maar het moet wel lukken denk ik
Ik ga hier verder maar niet op in, daar is het het topic niet voor. Laten we het er maar op houden dat we duidelijk van mening verschillen over toedracht en inhoud.quote:
[..]
Ik reageerde op de opvatting van thenxzero dat het gebruik van vectoren het eenvoudigst zou zijn. Maar los daarvan begrijp ik de kritiek niet. Je leidt namelijk zelf eerst een andere goniometrische identiteit af, tan α1∙tan α2 = 1 - cos(α1 + α2)/cos α1∙cos α2, die zo mogelijk nog veel onbekender is dan de formules voor tan(α-β) (resp. tan(α+β)) die gewoon tot het standaardrepertoire van goniometrische identiteiten behoren.
[..]
Zo 'natuurlijk' is dat niet. Als geldt a1a2 = -1 dan is 1 : a1 = -a2 : 1, zodat in je figuur de rechthoekige driehoek met hoekpunten (0,2), (1,2), (1, f(1)) gelijkvormig is met de rechthoekige driehoek met hoekpunten (1, g(1)), (1,2), (0,2), waaruit volgt dat α1 + α2 = π/2. Is omgekeerd α1 + α2 = π/2, dan zijn de genoemde driehoeken gelijkvormig, waaruit volgt dat 1 : a1 = -a2 : 1 en dus a1a2 = -1. Daar heb ik 'Pythagoras' niet voor nodig.
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
u(x, y) = min{2x, y}, bepaal u'y(8, 20).
u'y(8, 20) = 0 (volgens de uitwerkingen)
Moet dit niet u'y(8, 20) = 1 zijn?
u'y(8, 20) = 0 (volgens de uitwerkingen)
Moet dit niet u'y(8, 20) = 1 zijn?
Jij leest die posts ook echt?!?!quote:
[..]
Ik ga hier verder maar niet op in, daar is het het topic niet voor. Laten we het er maar op houden dat we duidelijk van mening verschillen over toedracht en inhoud.
Op 
Bepaal de afgeleide van y(x) = e2x−1
Volgens dictaat: y′(x) = (2x−1)e2x−1(2) = (4x-2)e2x−1
Ik dacht: y'(x) = 2(e2x-1), want de afgeleide van ex = ex
Wie zit er fout?
Volgens dictaat: y′(x) = (2x−1)e2x−1(2) = (4x-2)e2x−1
Ik dacht: y'(x) = 2(e2x-1), want de afgeleide van ex = ex
Wie zit er fout?
Thanks.
Waarom kan een universiteit geen fatsoenlijke uitwerkingen online zetten? Het stikt echt van de fouten.
Waarom kan een universiteit geen fatsoenlijke uitwerkingen online zetten? Het stikt echt van de fouten.
Klunzige fout zelfs. Dit is geen tikfoutje of zo maar echt een technische fout.quote:
Thanks.
Waarom kan een universiteit geen fatsoenlijke uitwerkingen online zetten? Het stikt echt van de fouten.
f '(x) = (e2x-1) ' = (2x-1) ' * de2x-1/d(2x-1) = 2e2x-1quote:
Bepaal de afgeleide van y(x) = e2x−1
Volgens dictaat: y′(x) = (2x−1)e2x−1(2) = (4x-2)e2x−1
Ik dacht: y'(x) = 2(e2x-1), want de afgeleide van ex = ex
Wie zit er fout?
Het dictaat heeft het fout. Beste blunder van die Uni
.
Casus:
8000 births, 3000 single mom, 5000 /w partner
Out of 3000 single moms, 1450 gave birth to son
Out of 5000 /w partner, 2250 gave birth to son.
Test at 5% significance
(a) Test whether the probability for a mom /w partner getting a son exceeds 50%
(b) Test whether the probability for a single mom getting a son is smaller than 50%.
(c) Test whether the probability of getting a son differs between the two groups of mothers.
(a) Nee
(b) Nee
(c) Nee
Dacht ik, maar nu twijfel of ik de juiste methode gebruikt heb..
8000 births, 3000 single mom, 5000 /w partner
Out of 3000 single moms, 1450 gave birth to son
Out of 5000 /w partner, 2250 gave birth to son.
Test at 5% significance
(a) Test whether the probability for a mom /w partner getting a son exceeds 50%
(b) Test whether the probability for a single mom getting a son is smaller than 50%.
(c) Test whether the probability of getting a son differs between the two groups of mothers.
(a) Nee
(b) Nee
(c) Nee
Dacht ik, maar nu twijfel of ik de juiste methode gebruikt heb..
Ik heb een 95% betrouwbaarheidsinterval van de fractie p (zoon) geconstrueerd. Bij (a) krijg ik 0.496-0.523, bij (b) .465-.5012quote:
Je intervallen zijn sowieso tweezijdig, dus klopt dat niet bij de eenzijdige toetsen in a en b. Maar misschien zou je eens kruistabellen o.i.d. moeten proberen?
Je hebt hier een leuke test voor, p. 498 van het grijze deel van je boek als ik het goed heb.
Normale benadering van dit geval.
Normale benadering van dit geval.
Beneath the gold, bitter steel
Thanks man, dit was idd wat ik zocht.quote:
Je hebt hier een leuke test voor, p. 498 van het grijze deel van je boek als ik het goed heb.
Normale benadering van dit geval.
Bij (b) krijg ik uit dat z=-1.83 en het significantieniveau komt uit op -1.645. Dus -1.83<-1.645. De verwachting bij verwerpen van H0 dan zou z<-1.645 moeten zijn toch? Dus verwerpen in dit geval en accepteren Ha.
Het moet toch ook pooled variance test zijn?quote:
c is leuk, gepoolde variantie nemen anders trekt Heij puntjes af
Het is tenslotte niet dezelfde groep die je twee keer test.
Correct.quote:
[..]
Het moet toch ook pooled variance test zijn?
Het is tenslotte niet dezelfde groep die je twee keer test.
Beneath the gold, bitter steel
Nee, de conclusie is altijd 'verwerp H0' of 'verwerp H0 niet'.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Daar zit nog een bepaald filosofisch verschil tussen. Aangezien de inferentiële methode bestaat uit het verwerpen van H0, kan het resultaat van die methode nooit zijn dat je H0 accepteert. De methode heeft maar twee uitkomsten, of je verwerpt wel of je verwerpt niet.
Maar over die filosofie moet je je na een tijdje maar heen zetten. Ik zeg na een toets gewoon altijd H0 is waar of H1 is waar, iedereen snapt toch wat je daarmee bedoelt.
Maar over die filosofie moet je je na een tijdje maar heen zetten. Ik zeg na een toets gewoon altijd H0 is waar of H1 is waar, iedereen snapt toch wat je daarmee bedoelt.
Jongens, ik heb ENORM veel problemen met mijn schakeljaar, de wiskundige vakken steek ik ENORM veel tijd in, de theorie, vooral achter Lineaire Algebra, is onbegrijpelijk. Weet niet hoe ik dit moet oppakken, werk soms tot 10 uur 's avonds op de TU door met het huiswerk, en voornamelijk de theoretsiche vragen zijn moeilijk en onbegrijpelijk... dit is trowuens mijn tweede keer... hoe pak ik dit nou op?
Ja je toetst of H0 verworpen kan worden dus de uitkomst is wel of niet verwerpen. Toch snap ik het niet helemaal waarom je niet het woord accepteren mag gebruiken, zeker als je dat resultaat wel in je verdere berekeningen voor waar aanneemt.quote:
Daar zit nog een bepaald filosofisch verschil tussen. Aangezien de inferentiële methode bestaat uit het verwerpen van H0, kan het resultaat van die methode nooit zijn dat je H0 accepteert. De methode heeft maar twee uitkomsten, of je verwerpt wel of je verwerpt niet.
Maar over die filosofie moet je je na een tijdje maar heen zetten. Ik zeg na een toets gewoon altijd H0 is waar of H1 is waar, iedereen snapt toch wat je daarmee bedoelt.
Even een voorbeeld:
H0: P is waar
H1: P is niet waar
Je gaat een toets doen en je kan H0 niet verwerpen. Vervolgens neem je aan dat P waar is in je verdere berekeningen. Dan heb je de uitspraak "P is waar" toch niet alleen niet verworpen, maar ook geaccepteerd? Dat je het niet zeker weet dat P echt waar is, dat klopt. Maar ook als je H0 verwerpt weet je niet zeker of dat terecht is en dat P niet waar is.
Dat jij H0 is waar of H1 is waar zegt is eigenlijk hetzelfde als zeggen dat je H0 of H1 accepteert, dus dat mag dan ook niet. En wat is de filosofie precies?
Blijven oefenen en doorzetten. Hoe meer je oefent hoe sneller je het op gaat pikken... je moet die manier van denken trainenquote:
Jongens, ik heb ENORM veel problemen met mijn schakeljaar, de wiskundige vakken steek ik ENORM veel tijd in, de theorie, vooral achter Lineaire Algebra, is onbegrijpelijk. Weet niet hoe ik dit moet oppakken, werk soms tot 10 uur 's avonds op de TU door met het huiswerk, en voornamelijk de theoretsiche vragen zijn moeilijk en onbegrijpelijk... dit is trowuens mijn tweede keer... hoe pak ik dit nou op?
.
Veel vragen lukt het mij om te maken... de manier om het op te schrijven en te verklaren, DAAR heb ik problemen mee, en daar verneuk ik tentamens mee, terwijl ik de sommen gewoon kan maken...quote:
[..]
Blijven oefenen en doorzetten. Hoe meer je oefent hoe sneller je het op gaat pikken... je moet die manier van denken trainen
http://liesandstats.wordp(...)r-fail-to-reject-it/quote:
[..]
Ja je toetst of H0 verworpen kan worden dus de uitkomst is wel of niet verwerpen. Toch snap ik het niet helemaal waarom je niet het woord accepteren mag gebruiken, zeker als je dat resultaat wel in je verdere berekeningen voor waar aanneemt.
Even een voorbeeld:
H0: P is waar
H1: P is niet waar
Je gaat een toets doen en je kan H0 niet verwerpen. Vervolgens neem je aan dat P waar is in je verdere berekeningen. Dan heb je de uitspraak "P is waar" toch niet alleen niet verworpen, maar ook geaccepteerd? Dat je het niet zeker weet dat P echt waar is, dat klopt. Maar ook als je H0 verwerpt weet je niet zeker of dat terecht is en dat P niet waar is.
Dat jij H0 is waar of H1 is waar zegt is eigenlijk hetzelfde als zeggen dat je H0 of H1 accepteert, dus dat mag dan ook niet. En wat is de filosofie precies?
Het is wat stelliger om te zeggen dat iets waar is, dan dat er niet genoeg bewijs is om de veronderstelde situatie te verwerpen. Je weet niet of iets waar is of niet, je weet enkel dat er geen reden is om de veronderstelde situatie te verwerpen indien er geen significante afwijkingen zijn gevonden.
Waarom zou je er niet mee doorrekenen als je niet kunt aantonen dat het niet waar is?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik heb m'n post al veranderdquote:
Waarom zou je er niet mee doorrekenen als je niet kunt aantonen dat het niet waar is?
Ik vroeg mij dat zelf ook af.
Schakeljaar waarvan precies?quote:
Jongens, ik heb ENORM veel problemen met mijn schakeljaar, de wiskundige vakken steek ik ENORM veel tijd in, de theorie, vooral achter Lineaire Algebra, is onbegrijpelijk. Weet niet hoe ik dit moet oppakken, werk soms tot 10 uur 's avonds op de TU door met het huiswerk, en voornamelijk de theoretsiche vragen zijn moeilijk en onbegrijpelijk... dit is trowuens mijn tweede keer... hoe pak ik dit nou op?
Beneath the gold, bitter steel
3.11 Splits de volgende reele polynomen in re ¨ ele lineaire factoren en re ¨ ele kwa- ¨
dratische factoren met een negatieve discriminant
Bij z^4+2z^2+1 = (z^2+1)^2
Bij z^4-2z^2+1 = ((z-1)^2)*((z+1)^2)
Waarom bij de 2e niet gewoon (z^2-1)^2?
dratische factoren met een negatieve discriminant
Bij z^4+2z^2+1 = (z^2+1)^2
Bij z^4-2z^2+1 = ((z-1)^2)*((z+1)^2)
Waarom bij de 2e niet gewoon (z^2-1)^2?
Heel eenvoudig, omdat je bij de tweede conform de opdracht kunt factoriseren in lineaire factoren met reële coëfficiënten, en bij de eerste niet. z2 - 1 heeft dan ook geen negatieve discriminant.quote:
3.11 Splits de volgende reële polynomen in reële lineaire factoren en reële kwadratische factoren met een negatieve discriminant
Bij z^4+2z^2+1 = (z^2+1)^2
Bij z^4-2z^2+1 = ((z-1)^2)*((z+1)^2)
Waarom bij de 2e niet gewoon (z^2-1)^2?
Oh, misschien had ik de opdracht moeten lezenquote:
[..]
Heel eenvoudig, omdat je bij de tweede conform de opdracht kunt factoriseren in lineaire factoren met reële coëfficiënten, en bij de eerste niet. z2 - 1 heeft dan ook geen negatieve discriminant.
Bewijs dat de som van k=1 t/m N met k^3 gelijk is aan (de som van k=1 t/m N met k)^2
Mag ik dan gebruiken dat de som van k=1 t/m N met k gelijk is aan 1/2n(n+1)?
Mag ik dan gebruiken dat de som van k=1 t/m N met k gelijk is aan 1/2n(n+1)?
Het mag wel (want het is makkelijk aan te tonen), maar ik vraag me af of inductie niet simpeler is.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik snap het punt, maar je zou ook kunnen zeggen dat je met accepteren niet bedoelt dat het waar is, maar dat er niet voldoende reden is om iets anders aan te nemen.quote:
[..]
http://liesandstats.wordp(...)r-fail-to-reject-it/
Het is wat stelliger om te zeggen dat iets waar is, dan dat er niet genoeg bewijs is om de veronderstelde situatie te verwerpen. Je weet niet of iets waar is of niet, je weet enkel dat er geen reden is om de veronderstelde situatie te verwerpen indien er geen significante afwijkingen zijn gevonden.
Zo werkt het ook in de natuurkunde. Een theorie als quantummechanica wordt geaccepteerd door onderzoekers, mede omdat de theorie overeenkomt met experimenten (oftewel: er is niet voldoende bewijs om H0: quantummechanica klopt te verwerpen), maar dat betekent nog niet dat de theorie echt klopt.
Dus: je kan best iets accepteren zonder dat je zeker weet of het zo is. Het zit 'm denk ik in je definitie van accepteren.
[ Bericht 4% gewijzigd door thenxero op 15-10-2011 12:47:00 ]
Het nadeel van een bewijs met inductie is dat het niet heuristisch is, dus je moet al weten wat de formule is voor e.g. de som van de kwadraten of kubieken (derde machten) van de eerste n natuurlijke getallen alvorens je een bewijs met inductie kunt geven. Een afleiding van een dergelijke formule is toch wat anders. In dit geval weet Physics al wat hij moet bewijzen, en is gebruik van inductie dus inderdaad de aangewezen weg, maar eerder vroeg Physics ook al naar een uitdrukking voor de som van de kwadraten van de eerste n natuurlijke getallen en hoe je aan die formule komt, en dan is het geven van de kant en klare formule met de opmerking dat je deze kunt bewijzen met inductie geen antwoord op de eigenlijke vraag.quote:
Het mag wel (want het is makkelijk aan te tonen), maar ik vraag me af of inductie niet simpeler is.
[ Bericht 0% gewijzigd door Riparius op 15-10-2011 20:01:30 ]
Ja, en dat is inderdaad zelfs handig als je het gevraagde middels inductie wil bewijzen. Als je wil zien waarom en hoe het bewijs dan gaat moet je maar even hier kijken. Wil je daarentegen een afleiding van de somformule zonder gebruik van inductie, dan kan ik je aanraden eens naar het verschil van de vierde machten van opeenvolgende natuurlijke getallen te kijken en deze verschillen te sommeren. Je krijgt dan een zogeheten telescoopreeks waarin alle termen uitgezonderd de eerste en de laatste tegen elkaar weg vallen.quote:
Bewijs dat de som van k=1 t/m N met k^3 gelijk is aan (de som van k=1 t/m N met k)^2
Mag ik dan gebruiken dat de som van k=1 t/m N met k gelijk is aan 1/2n(n+1)?
Ik zie dat je met inductie ook de somformule nodig hebt van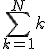 
. Met die formule is het bewijs vijf regeltjes.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik heb eerst die somformule bewezen en daarmee de oorspronkelijke vraag bewezen dmv volledige inductie.quote:
Ik zie dat je met inductie ook de somformule nodig hebt van
Ja bedankt, het is me zelf ook al gelukt!quote:
[..]
Ja, en dat is inderdaad zelfs handig als je het gevraagde middels inductie wil bewijzen. Als je wil zien waarom en hoe het bewijs dan gaat moet je maar even hier kijken. Wil je daarentegen een afleiding van de somformule zonder gebruik van inductie, dan kan ik je aanraden eens naar het verschil van de vierde machten van opeenvolgende natuurlijke getallen te kijken en deze verschillen te sommeren. Je krijgt dan een zogeheten telescoopreeks waarin alle termen uitgezonderd de eerste en de laatste tegen elkaar weg vallen.
[ Bericht 42% gewijzigd door Physics op 15-10-2011 19:19:04 ]
Beschouw de nutsfunctie u(x, y) = min{4x, 3y + 2}. Bereken u′y(1, 1)
Waarom is het u′y(1, 1) = 0 en niet 1?
Soortgelijke vraag van pagina 9:
Waarom is het u′y(1, 1) = 0 en niet 1?
Soortgelijke vraag van pagina 9:
quote:
u(x, y) = min{2x, y}, bepaal u'y(8, 20).
u'y(8, 20) = 0 (volgens de uitwerkingen)
Moet dit niet u'y(8, 20) = 1 zijn?
Dit is het antwoord van een tentamen van vorig jaar, dus ik kan me niet voorstellen dat het fout is.quote:
Mijn vorige antwoord was fout 
min{2x,y} geeft de kleinste van 2x en y, voor (x,y) = (8,20) geeft hij dus 16; de 2x is actief daar, dus de afgeleide naar y is 0.
min{2x,y} geeft de kleinste van 2x en y, voor (x,y) = (8,20) geeft hij dus 16; de 2x is actief daar, dus de afgeleide naar y is 0.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Beschouw de nutsfunctie u(x, y) = min{5x, 6y + 2}. Bereken u′y(3, 2)
5x > 6y+2, dan u′y(3, 2) = 6
5x < 6y+2, dan u′y(3, 2) = 0
5.3 = 15
6.2 + 2 = 14
15 > 14
u′y(3, 2) = 6
Redeneer ik zo goed?
5x > 6y+2, dan u′y(3, 2) = 6
5x < 6y+2, dan u′y(3, 2) = 0
5.3 = 15
6.2 + 2 = 14
15 > 14
u′y(3, 2) = 6
Redeneer ik zo goed?
ja; en u′y(4, 3) is niet gedefinieerd.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dat je hier 5x = 6y+2 mist.quote:
5x > 6y+2, dan u′y(3, 2) = 6
5x < 6y+2, dan u′y(3, 2) = 0
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
