SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



In vervolg op wat GlowMouse zegt:quote:Op vrijdag 7 oktober 2011 15:22 schreef Tauchmeister het volgende:
ex ln(x + 1/2) = 0
⇒ ln(x + 1/2) = 0
Waarom kan ik ex hier weglaten?
en e^x kan nooit 0 zijn, dus moet het andere stuk wel gelijk aan 0 zijn en kan je e^x gewoon weg laten.


Waarom geldt:
Ik snap er niks van
(hints worden ook erg op prijs gesteld )
)
[ Bericht 16% gewijzigd door minibeer op 07-10-2011 23:00:41 ]
Ik snap er niks van
(hints worden ook erg op prijs gesteld
[ Bericht 16% gewijzigd door minibeer op 07-10-2011 23:00:41 ]
Finally, someone let me out of my cage


Ik zal alvast een aanzet geven:
Er staat een binomiaalcoëfficient in de formule, dus we hebben
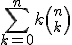
Nu prop ik daar vrolijk een x-macht bij:
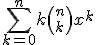
Dit moeten we dan evalueren in x=1.
Nog meer hints? .
.
Er staat een binomiaalcoëfficient in de formule, dus we hebben
Nu prop ik daar vrolijk een x-macht bij:
Dit moeten we dan evalueren in x=1.
Nog meer hints?


Het kan zelfs nog simpeler bedenk ik me opeens, je kan factoren k in de teller en noemer tegen elkaar wegstrepen, dan staat het er zowat.


Als je hints wil hebben is het wel handig als iedereen je plaatje kan zien. Ik zie het hier niet omdat de links naar plaatjes van Wolfram maar een beperkte tijd geldig zijn.quote:Op vrijdag 7 oktober 2011 17:31 schreef minibeer het volgende:
Waarom geldt:
[ afbeelding ]
Ik snap er niks van
(hints worden ook erg op prijs gesteld)


Excuses, ik kan geen latex, anders zou ik het wel even ingetypt hebben. Gefixt nu.quote:Op vrijdag 7 oktober 2011 19:24 schreef Riparius het volgende:
[..]
Als je hints wil hebben is het wel handig als iedereen je plaatje kan zien. Ik zie het hier niet omdat de links naar plaatjes van Wolfram maar een beperkte tijd geldig zijn.
[ Bericht 0% gewijzigd door minibeer op 07-10-2011 23:01:48 ]
Finally, someone let me out of my cage


Kan ook makkelijk zonder inductie.quote:Op vrijdag 7 oktober 2011 17:31 schreef minibeer het volgende:
Waarom geldt:
[ afbeelding ]
Ik snap er niks van
(hints worden ook erg op prijs gesteld)
Hint:
Volgens het Binomium van Newton.


Ik zie het nu wel inderdaad, ik zie het helaas alleen de andere kant op, als ik met jou hint begin en die vervolgens vermenigvuldig met n zie ik vrij makkelijk dat het gelijk is aanquote:Op vrijdag 7 oktober 2011 23:41 schreef thenxero het volgende:
[..]
Kan ook makkelijk zonder inductie.
Hint:
Volgens het Binomium van Newton.
Andersom echter nog niet, maar dat zal wel aan mijn inzicht liggen (sowieso heb ik nog nooit met die binomiaalcoëfficiënten gerekend op deze manier, dus ik moet gewoon die rekenregels nog wat beter leren kennen)
Finally, someone let me out of my cage


Als je het de ene kant opziet dan is dat genoeg, want je werkt met = tekens  . Vaak werkt één bepaalde kant op heel intuïtief, maar de andere kant op heel erg getruct... dat is normaal.
. Vaak werkt één bepaalde kant op heel intuïtief, maar de andere kant op heel erg getruct... dat is normaal.


True. Het grappige is dat ik deze vraag op een tentamen trouwens goed hadquote:Op vrijdag 7 oktober 2011 23:55 schreef thenxero het volgende:
Als je het de ene kant opziet dan is dat genoeg, want je werkt met = tekens. Vaak werkt één bepaalde kant op heel intuïtief, maar de andere kant op heel erg getruct... dat is normaal.
Finally, someone let me out of my cage


Dat is eigenlijk hetzelfde idee als inductie, alleen doe je het met inductie algemener. Dat het in de eerste 5 a 6 gevallen klopt garandeert niets over het 7e geval of daarna. Inductie is denk ik ook nog sneller dan die gevallen uitschrijven.quote:Op zaterdag 8 oktober 2011 00:39 schreef minibeer het volgende:
[..]
True. Het grappige is dat ik deze vraag op een tentamen trouwens goed had. Ik was er alleen op gekomen door de eerste 5 of 6 gevallen uit te schrijven en daar de formule uit te concluderen (het was geen wiskunde, dus er werd gelukkig geen bewijs gevraagd), maar ik had geen idee waarom deze formule nou eigenlijk gold.


Het is m.i. beter en plezieriger om zulke sommen met combinatoriek te bewijzen, door daadwerkelijk te kijken naar wat je telt. Je kunt in dit geval wel beredeneren dat je zowel links als rechts het aantal paren telt (A,b) met 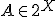 ,
, 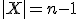 en
en 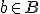 ,
, 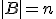


Ik vind het prettiger om een paar vergelijkingen op te schrijven dan om een beredenering te houden wat je aan het tellen bent.quote:Op zaterdag 8 oktober 2011 00:48 schreef twaalf het volgende:
Het is m.i. beter en plezieriger om zulke sommen met combinatoriek te bewijzen, door daadwerkelijk te kijken naar wat je telt. Je kunt in dit geval wel beredeneren dat je zowel links als rechts het aantal paren telt (A,b) met,
en
,


Wat heb je aan de formule die je bewijst als je niet weet voor welk probleem je precies een andere uitdrukking hebt gevonden? Natuurlijk maakt het uiteindelijk niet uit of je het met formulemanipulatie of tellen doet, maar dit is nou samen met gonio juist een vakgebied waar je eens iets anders kunt doen dan manipuleren.


Hmm, zo heb ik er nooit tegenaan gekeken, maar ik weet niet of ik dat zo gelijk kan zienquote:Op zaterdag 8 oktober 2011 00:48 schreef twaalf het volgende:
Het is m.i. beter en plezieriger om zulke sommen met combinatoriek te bewijzen, door daadwerkelijk te kijken naar wat je telt. Je kunt in dit geval wel beredeneren dat je zowel links als rechts het aantal paren telt (A,b) met,
en
,
Finally, someone let me out of my cage


In een aquarium staat het water 40 cm hoog. Het aquarium wordt leeggeheveld.
Na 10 min is het leeg.
Welke formule geeft het verband tussen de waterhoogte h in cm en de tijd t in minuten?
Na 10 min is het leeg.
Welke formule geeft het verband tussen de waterhoogte h in cm en de tijd t in minuten?


Het wordt leeggeheveld, dat lijkt me niet lineair te verlopen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


In dit geval wel.quote:Op zaterdag 8 oktober 2011 12:01 schreef GlowMouse het volgende:
Het wordt leeggeheveld, dat lijkt me niet lineair te verlopen.


Ah, je hebt gelijk.
Sorry, mijn fout.
Zo zie je maar weer dat ik niet bepaald de briljanste ben in wiskunde.
Edit : Geen dank !
Sorry, mijn fout.
Zo zie je maar weer dat ik niet bepaald de briljanste ben in wiskunde.
Edit : Geen dank !


Ik snap het, dank u!quote:Op zaterdag 8 oktober 2011 12:00 schreef Quaintrelle het volgende:
H = 40 - (4t)
Je startwaarde is 40 en het waterhoogte daalt met 40/10 = 4 cm per minuut,


leg even uit waarom de haakjes er staanquote:
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


De haakjes staan er om ervoor te zorgen dat de vermenigvuldiging eerst plaatsvindt.
Indien je "40 - 4t" zou opschrijven, krijg je :
40 - 4 = 36 en dan
36 * t
Indien je "40 - 4t" zou opschrijven, krijg je :
40 - 4 = 36 en dan
36 * t


Ik kom niet uit de volgende limiet
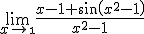
(x²-1) = (x-1)(x+1), maar verder kom ik niet. Sin (a -b) = sin a cos a - cos a sin b leverde me niets op. L'hospital's rule ken ik niet. Kan iemand helpen?
(x²-1) = (x-1)(x+1), maar verder kom ik niet. Sin (a -b) = sin a cos a - cos a sin b leverde me niets op. L'hospital's rule ken ik niet. Kan iemand helpen?


oj, zie http://www.khanacademy.or(...)t=Developmental+Mathquote:Op zaterdag 8 oktober 2011 12:30 schreef Quaintrelle het volgende:
De haakjes staan er om ervoor te zorgen dat de vermenigvuldiging eerst plaatsvindt.
Indien je "40 - 4t" zou opschrijven, krijg je :
40 - 4 = 36 en dan
36 * t
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


quote:Op zaterdag 8 oktober 2011 12:31 schreef Anoonumos het volgende:
Ik kom niet uit de volgende limiet
(x²-1) = (x-1)(x+1), maar verder kom ik niet. Sin (a -b) = sin a cos a - cos a sin b leverde me niets op. L'hospital's rule ken ik niet. Kan iemand helpen?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Oh ja.quote:Op zaterdag 8 oktober 2011 12:31 schreef GlowMouse het volgende:
[..]
oj, zie http://www.khanacademy.or(...)t=Developmental+Math
Tja, dit bevestigt mijn eerdere stelling.


De kromme K bestaat uit alle punten 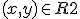 die voldoen aan
die voldoen aan
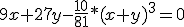
Deze kromme heeft een raaklijn L in het punt (0, 0).
(a) Geef de vergelijking van L in de vorm y = rx + b.
(b) Er zijn twee punten op K waar de raaklijnen zo zijn dat ze de lijn L
ergens loodrecht snijden. Bereken de co¨ordinaten van deze punten.
Met impliciet differentieren krijg ik bij a) L = -1/3 x.
Dus voor de andere raaklijn geldt helling = 3. Ik weet niet hoe ik nu x en y kan vinden.
[ Bericht 14% gewijzigd door Anoonumos op 08-10-2011 15:57:47 ]
Deze kromme heeft een raaklijn L in het punt (0, 0).
(a) Geef de vergelijking van L in de vorm y = rx + b.
(b) Er zijn twee punten op K waar de raaklijnen zo zijn dat ze de lijn L
ergens loodrecht snijden. Bereken de co¨ordinaten van deze punten.
Met impliciet differentieren krijg ik bij a) L = -1/3 x.
Dus voor de andere raaklijn geldt helling = 3. Ik weet niet hoe ik nu x en y kan vinden.
[ Bericht 14% gewijzigd door Anoonumos op 08-10-2011 15:57:47 ]


Calculus van James Stewart
Section 7.1
Example 6
Ik probeer al een half uur lang te begijpen hoe men aan het antwoor na de zin: cos^2x = 1-sin^2x
Waarom staan er plots 2 integralen met daarvoor (n-1)
Section 7.1
Example 6
Ik probeer al een half uur lang te begijpen hoe men aan het antwoor na de zin: cos^2x = 1-sin^2x
Waarom staan er plots 2 integralen met daarvoor (n-1)


Impliciet differentiëren van de vergelijking van de curve naar x en subsitutie van y' = 3 levert als voorwaarde voor de coördinaten van de gevraagde punten op de curve:quote:Op zaterdag 8 oktober 2011 15:24 schreef Anoonumos het volgende:
De kromme K bestaat uit alle puntendie voldoen aan
Deze kromme heeft een raaklijn L in het punt (0, 0).
(a) Geef de vergelijking van L in de vorm y = rx + b.
(b) Er zijn twee punten op K waar de raaklijnen zo zijn dat ze de lijn L
ergens loodrecht snijden. Bereken de co¨ordinaten van deze punten.
Met impliciet differentieren krijg ik bij a) L = -1/3 x.
Dus voor de andere raaklijn geldt helling = 3. Ik weet niet hoe ik nu x en y kan vinden.
(x + y)2 = (3/4)∙81
Nu jij weer.
[ Bericht 0% gewijzigd door Riparius op 08-10-2011 18:21:13 ]


Heeft iemand hier dat trapje waar staat hoeveel x je moet gaan van centiliter naar ml naar liter enz en meters naar centimeters naar decimeters enz.. ?
Dank
Dank
graag op anoniem


http://en.wikipedia.org/wiki/SI_prefix#List_of_SI_prefixesquote:Op zaterdag 8 oktober 2011 16:48 schreef KingRoland het volgende:
Heeft iemand hier dat trapje waar staat hoeveel x je moet gaan van centiliter naar ml naar liter enz en meters naar centimeters naar decimeters enz.. ?
Dank


Ja. Je bedoelt vast:quote:Op zaterdag 8 oktober 2011 16:58 schreef Sokz het volgende:
Domein van sq.(x-3)(x-5) is toch (x-3)(x-5) > 0?
dus:
(-∞,3) (5,+∞)?



 Op
Op 