SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Nee, pak bv. R+, met x=5 en y=-1. dan zitten x en x+y er wel in, maar y niet. Hier kun je aantonen dat je op een tegenspraak uitkomt als x+y in U1 zit, maar dat moet je dan wel doen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Graag wil ik nog even terugkomen op deze opgave omdat het toch met aanzienlijk minder rekenwerk blijkt te kunnen dan ik gisteren had aangegeven. Laten we de factor ½ van alle termen van de reeks even buiten beschouwing, dan gaat het om het sommeren van een reeks waarvan de termen van de volgende gedaante zijn:quote:Op zaterdag 24 september 2011 16:22 schreef thenxero het volgende:
Hoe bereken ik dat?
Binom staat voor het binomiaalcoëfficiënt.
Het is geen meetkundige rij ... maar het staat als rekenopgave in mijn textboek, dus zou toch met pen en papier moeten kunnen.
(1) k2(k -1)(1 - p)k-2
Als het nu ging om het sommeren van een reeks met termen van de gedaante k(k -1)(1 - p)k-2, dan was het eenvoudig, aangezien de termen dan zijn op te vatten als de tweede afgeleide van termen van de gedaante (1 - p)k, die een meetkundige reeks vormen. Maar in (1) hebben de termen een extra factor k.
Nemen we daarentegen de derde afgeleide van een meetkundige reeks met termen met een exponent k+1, dan krijgen we in de afgeleide reeks bij elke term een factor (k+1)k(k-1), en dus ook niet de gewenste factor k2(k-1). Maar nu kunnen we opmerken dat:
(2) k2(k-1) = (k+1-1)k(k-1) = (k+1)k(k-1) - k(k-1)
En dus hebben we ook:
(3) k2(k-1)(1 - p)k-2 = (k+1)k(k-1)(1 - p)k-2 - k(k-1)(1 - p)k-2
Dit betekent niets anders dan dat je de reeks met termen van de gedaante (1) kunt opvatten als het verschil van twee reeksen waarvan de eerste de derde afgeleide is van een geometrische reeks met termen van de gedaante -(1 - p)k+1 terwijl de tweede reeks de tweede afgeleide is van een geometrische reeks met termen van de gedaante (1 - p)k. Dus:
(4) Σk=2∞ k2(k-1)(1 - p)k-2 = Σk=2∞ (k+1)k(k-1)(1 - p)k-2 - Σk=2∞ k(k-1)(1 - p)k-2 (|1 - p| <1)
De som van elk van beide reeksen in het rechterlid van (4) is eenvoudig te bepalen. Nemen we eerst de geometrische reeks met termen van de gedaante -(1 - p)k+1, k = 2..∞. De eerste term hiervan is -(1 - p)3 en de reden (1 - p), dus:
(5) Σk=2∞ -(1 - p)k+1 = -(1 - p)3/p = p2 - 3p + 3 - p-1 (|1 - p| < 1)
Beide leden driemaal differentiëren naar p levert dan:
(6) Σk=2∞ (k+1)k(k-1)(1 - p)k-2 = 6p-4 (|1 - p| < 1)
Nu de geometrische reeks met termen van de gedaante (1 - p)k, k = 2..∞. De eerste term hiervan is (1 - p)2 en de reden (1 - p), dus:
(7) Σk=2∞ (1 - p)k = (1 - p)2/p = p - 2 + p-1 (|1 - p| < 1)
Beide leden tweemaal differentiëren naar p geeft:
(8) Σk=2∞ k(k-1)(1 - p)k-2 = 2p-3 (|1 - p| < 1)
Uit (4), (6) en (8) volgt nu:
(9) Σk=2∞ k2(k-1)(1 - p)k-2 = 6p-4 - 2p-3 = (6 - 2p)/p4 (|1 - p| < 1)
Beide leden vermenigvuldigen met ½ en terugsubstitueren van ½k(k - 1) = (k2) levert dan:
(10) Σk=2∞ k(k2)(1 - p)k-2 = (3 - p)/p4 (|1 - p| < 1)
QED
[ Bericht 0% gewijzigd door Riparius op 26-09-2011 03:02:11 ]
De tegenspraak zou kunnen zijn dat U1 toch een deelverzameling is van U2 of andersom, of dat y toch in U1 zit of x toch in U2. Maar ik zie niet hoe dit volgt als x + y in U1 zit. Ik begrijp dat ik lastig ben, maar ik waardeer jullie hulp.quote:
Nee, pak bv. R+, met x=5 en y=-1. dan zitten x en x+y er wel in, maar y niet. Hier kun je aantonen dat je op een tegenspraak uitkomt als x+y in U1 zit, maar dat moet je dan wel doen.
x zit in U1-U2 en y in U2-U1.
Stel x+y zit in U1, kun je dan aantonen dat y ook in U1 zit, om zo op een tegenspraak te komen? Je weet dat x in U1 zit, dus -x ook.
Stel x+y zit in U1, kun je dan aantonen dat y ook in U1 zit, om zo op een tegenspraak te komen? Je weet dat x in U1 zit, dus -x ook.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Aha. Dus (x+y) + -x = y ook want het is een deelruimte. Ik hoop dat het me binnenkort zelf lukt om zoiets te bedenken. Bedankt. 
Brengen de vectoren (1,0,-1), (2,1,1) en (1,0,1) R³ voort?
Ja, voor elke x.y,z in R³ geldt dat het een lineaire combinatie is van deze 3 vectoren. (neem scalars c1 = 1/2 (x - y - z), c2 = y , c3 = 1/2 (x - 3y + z)
Brengen de vectoren (1,2,3), (4,5,6) en (7,8,9) R³ voort?
Nee, c1 c2 en c3 blijf ik afhankelijk van elkaar houden. Dus er is geen lineaire combinatie mogelijk.
Doe ik dit goed? In het dictaat staat het amper uitgelegd, dus ik moet me redden met filmpjes van Khan Academy.
Ja, voor elke x.y,z in R³ geldt dat het een lineaire combinatie is van deze 3 vectoren. (neem scalars c1 = 1/2 (x - y - z), c2 = y , c3 = 1/2 (x - 3y + z)
Brengen de vectoren (1,2,3), (4,5,6) en (7,8,9) R³ voort?
Nee, c1 c2 en c3 blijf ik afhankelijk van elkaar houden. Dus er is geen lineaire combinatie mogelijk.
Doe ik dit goed? In het dictaat staat het amper uitgelegd, dus ik moet me redden met filmpjes van Khan Academy.
Waarom volgt daaruit dat ze R3 niet voortbrengen?quote:
Brengen de vectoren (1,2,3), (4,5,6) en (7,8,9) R³ voort?
Nee, c1 c2 en c3 blijf ik afhankelijk van elkaar houden. Dus er is geen lineaire combinatie mogelijk.
Als een element in R³ niet geschreven kan worden als een lineaire combinatie van 3 bepaalde vectoren, dan brengen die 3 vectoren R³ niet voort.
Leuk die oneliners van thabit die in één keer de vinger op de zere plek legt.
OT:Heeft iemand een leuke denk opgave over analystische meetkunde; rechte lijnen en cirkels?
OT:Heeft iemand een leuke denk opgave over analystische meetkunde; rechte lijnen en cirkels?
kloep kloep
Tja, wat zoek je, en voor wie is het bestemd (niveau)?quote:Op zondag 25 september 2011 19:29 schreef Borizzz het volgende:
OT:Heeft iemand een leuke denk opgave over analytische meetkunde; rechte lijnen en cirkels?
6 vwo; wiskunde Dquote:
[..]
Tja, wat zoek je, en voor wie is het bestemd (niveau)?
5 vwo mag ook.
kloep kloep
Pak dan het echte werk:quote:
http://aleph0.clarku.edu/~djoyce/java/elements/toc.html
Pak boek 1, lees alles door wat boven de 'propositions' staat en werk dan stap voor stap de propositions door.
Boek 3 gaat over cirkels.
Dat is Euclidische meetkunde, niet wat gewoonlijk wordt verstaan onder analytische meetkunde.quote:
[..]
Pak dan het echte werk:
http://aleph0.clarku.edu/~djoyce/java/elements/toc.html
Pak boek 1, lees alles door wat boven de 'propositions' staat en werk dan stap voor stap de propositions door.
Boek 3 gaat over cirkels.
Dit is euclidische meetkunde geen analystische. En ik vroeg geen bronmateriaal maar een denk opgave die uitdaagtquote:
[..]
Pak dan het echte werk:
http://aleph0.clarku.edu/~djoyce/java/elements/toc.html
Pak boek 1, lees alles door wat boven de 'propositions' staat en werk dan stap voor stap de propositions door.
Boek 3 gaat over cirkels.
Wel aardige site overigens, wist niet dat er een site was waar dit online stond.
kloep kloep
Kijk of ze de coördinaten van het middelpunt van de ingeschreven cirkel van een driehoek uit kunnen drukken in de coördinaten van de hoekpunten. Bespreek verschillende manieren om zoiets aan te pakken.quote:
[ Bericht 1% gewijzigd door Riparius op 26-09-2011 02:28:40 ]
Jawel, maar in het tweede deel zit wel de overweging of het ook op andere, slimmere manieren kan worden aangepakt.
Bijvoorbeeld dit: cirkel en lijn snijden in punt A en B. C: (x-2)^2 + (y+3)^2=23 en l: 3x+py=6.
De afstand tussen A en B is 5. Bereken p.
Zo'n opdracht zou ik graag nog wat moeilijker maken d.m.v een uitbreiding.
Bijvoorbeeld dit: cirkel en lijn snijden in punt A en B. C: (x-2)^2 + (y+3)^2=23 en l: 3x+py=6.
De afstand tussen A en B is 5. Bereken p.
Zo'n opdracht zou ik graag nog wat moeilijker maken d.m.v een uitbreiding.
kloep kloep
Er zijn uiteraard talloze sites waar je alle denkbare klassiekers kunt vinden. Ik vind dit wel een goede editie van de Elementen omdat die de oorspronkelijke Griekse tekst (ed. Heiberg) bevat, met een moderne Engelse vertaling.quote:
[..]
Wel aardige site overigens, wist niet dat er een site was waar dit online stond.
Ik heb de vergelijking e^(x+y)-e^(x-y)-(1/2) = e^(x+y) + e^(x-y) - (3/2)
Nu wil ik x uitdrukken in y.
Na wat vereenvoudigen komt er bij mij uit 2*e^(x-y) = 1
e^(x-y) = 1/2
(x-y) = ln(1/2)
x = ln(1/2) + y
Wolfram komt op x = log(2) + y
Wat doe ik fout?
Ik zie vast iets simpels over het hoofd, ik schaam me zelfs dat ik het vraag.
Nu wil ik x uitdrukken in y.
Na wat vereenvoudigen komt er bij mij uit 2*e^(x-y) = 1
e^(x-y) = 1/2
(x-y) = ln(1/2)
x = ln(1/2) + y
Wolfram komt op x = log(2) + y
Wat doe ik fout?
Ik zie vast iets simpels over het hoofd, ik schaam me zelfs dat ik het vraag.
log(2) = -log(1/2) dus daar zit ergens jouw fout.
Geeft wolfram niet per ongeluk y = log(2) + x?
Geeft wolfram niet per ongeluk y = log(2) + x?
Beneath the gold, bitter steel
Sorry inderdaad y = log(2) + xquote:
log(2) = -log(1/2) dus daar zit ergens jouw fout.
Geeft wolfram niet per ongeluk y = log(2) + x?
x = y - log(2)
Maar ik begrijp niet hoe ze x = ln(1/2) + y veranderen in x = y - log(2)
ln(1/2) geeft iets anders in m'n rekenmachine dan -log(2)
hun log heeft grondtal e
en log(ab) = b log(a), pak nu b=-1.
en log(ab) = b log(a), pak nu b=-1.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Aha! Ik dacht dat log automatisch grondtal 10 had.quote:
hun log heeft grondtal e
en log(ab) = b log(a), pak nu b=-1.
Bedankt.
log heeft in vrijwel alle applicaties grondtal e(=ln), als je een ander grondtal wil moet je dat meestal specifiek aangeven.quote:
[..]
Aha! Ik dacht dat log automatisch grondtal 10 had.
Bedankt.
Beneath the gold, bitter steel
Op de middelbare school moest ik altijd de 10log hebben om de pH-waarde of decibels uit te rekenenquote:
[..]
log heeft in vrijwel alle applicaties grondtal e(=ln), als je een ander grondtal wil moet je dat meestal specifiek aangeven.
. Verder is inderdaad bijna alles ln.
Vandaar vrijwel, de GR is inderdaad de enige uitzondering die ik zo kan benoemenquote:
[..]
Op de middelbare school moest ik altijd de 10log hebben om de pH-waarde of decibels uit te rekenen
Beneath the gold, bitter steel
Je kunt om elke ambiguïteit uit te sluiten bij WolframAlpha ook een grondtal meegeven, vergelijk dit met dit. Voor WolframAlpha is er geen verschil tussen ln en log bij de input, wat overigens weer niet consequent is omdat een grondtal anders dan e bij ln ook wordt geaccepteerd ...quote:
[..]
Aha! Ik dacht dat log automatisch grondtal 10 had.
Bedankt.
Aha, ik wist deze syntax nietquote:
[..]
Je kunt om elke ambiguïteit uit te sluiten bij WolframAlpha ook een grondtal meegeven, vergelijk dit met dit. Voor WolframAlpha is er geen verschil tussen ln en log bij de input, wat overigens weer niet consequent is omdat een grondtal anders dan e bij ln ook wordt geaccepteerd ...
Hierop terugkomend, kan ik hier gebruiken dat v1 - 2v2 + v3 = 0, dus brengen ze R³ niet voort. Ik weet dat dit waar is, maar we hebben dat nog niet behandeld. Ik zou echter niet weten hoe het anders moet.quote:Brengen de vectoren (1,2,3), (4,5,6) en (7,8,9) R³ voort?
Nee, c1 c2 en c3 blijf ik afhankelijk van elkaar houden. Dus er is geen lineaire combinatie mogelijk.
Weet je iets over de dimensie van een ruimte, en het aantal lineair onafhankelijke vectoren in een basis van die ruimte?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Nee, dat hebben we nog niet gehad.
Als ik hier laat zien dat elke vector te schrijven is als een lineaire combinatie van de 2 andere vectoren, dan heb ik toch aangetoond dat ze R³ niet voortbrengen?
Als ik hier laat zien dat elke vector te schrijven is als een lineaire combinatie van de 2 andere vectoren, dan heb ik toch aangetoond dat ze R³ niet voortbrengen?
Waarom?quote:
Als ik hier laat zien dat elke vector te schrijven is als een lineaire combinatie van de 2 andere vectoren, dan heb ik toch aangetoond dat ze R³ niet voortbrengen?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Twee van die vectoren brengen R² voort. Als je de derde vector toevoegt, liggen alle lineaire combinaties nog steeds in een vlak, omdat de derde een lineaire combinatie van de eerste twee is.
Nee, twee lineair onafhankelijke vectoren brengen een tweedimensionale deelruimte voort. Dat is niet R², omdat elementen van R² bestaan uit paren van twee reële getallen.quote:
Twee van die vectoren brengen R² voort.
Klopt.quote:Als je de derde vector toevoegt, liggen alle lineaire combinaties nog steeds in een vlak, omdat de derde een lineaire combinatie van de eerste twee is.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Aangezien het begrip "dimensie" nog niet behandeld is, moet hier nog wel worden aangetoond dat een vlak niet de hele ruimte is.
X is given n passwords and tries them at random. Find the mean and variance of Y (# number of trials required to a succesful password. If unsuccesful, passwords are eliminated
Dus µ=E(Y)= Som yp(y) = 1*1/n+2*1/n+3*1/n+...+n*1/n
Ofwel µ=E(Y)= .5(n+1)?
Dus µ=E(Y)= Som yp(y) = 1*1/n+2*1/n+3*1/n+...+n*1/n
Ofwel µ=E(Y)= .5(n+1)?
Zijn de n wachtwoorden verschillend, en klopt er tenminste eentje?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Exact één klopt, wachtwoorden zijn verschillend neem ik aan.quote:
Zijn de n wachtwoorden verschillend, en klopt er tenminste eentje?
Dan is je antwoord juist. Nu de variance nog.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
.quote:
Dan is je antwoord juist. Nu de variance nog.
V(Y)=E(Y^2)-µ^2
Bij E(Y^2) krijg je de som van de rij 1^2/n+2^2/n+3^2/n+...+n^2/n alleen weet ik niet hoe je die som kan berekenen, dus daar loop ik vast.
1²+2²+3²+4²+...+n² = n(n+1)(2n+1)/6
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Hoe kom je tot die formule? Ik herken dit nietquote:
1²+2²+3²+4²+...+n² = n(n+1)(2n+1)/6
Die kent iedereen, net als 1+2+3+...+n = n(n+1)/2.
Je kunt hem bewijzen met inductie.
Je kunt hem bewijzen met inductie.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Misschien kunnen jullie mij helpen met dit sommetje.
(x-12)*(30 – (1/2)*x), waarbij (30-(1/2)*x) ligt tussen 0 en 48.
Hiervan wil ik de afgeleide berekenen en vervolgens oplossen naar x.
Volgens mij is dit een heel simpel sommetje, maar door dat tussen 0 en 48 lukt het mij op een of andere manier niet...
(x-12)*(30 – (1/2)*x), waarbij (30-(1/2)*x) ligt tussen 0 en 48.
Hiervan wil ik de afgeleide berekenen en vervolgens oplossen naar x.
Volgens mij is dit een heel simpel sommetje, maar door dat tussen 0 en 48 lukt het mij op een of andere manier niet...
Ik zeg het trouwens verkeerd, de maximumwaarde van (30-(1/2)*x) ligt tussen 0 en 48, niet per se alle waardes.
Als (30-(1/2)*x) tussen 0 en 48 ligt, dan ligt x tussen -36 en 60 (zie je waarom?).
Wat bedoel je met de afgeleide oplossen naar x? Waar stel je het dan eerst aan gelijk?
Wat bedoel je met de afgeleide oplossen naar x? Waar stel je het dan eerst aan gelijk?
Dat kan je dus gewoon doen zoals je het altijd doet alleen zijn alleen je antwoorden met x tussen -36 en 60 geldig.
Ik snap het, maar zoals ik in mijn tweede post zei ligt de maximale waarde tussen 0 en 48, verandert dat er nog iets aan?
Als (30-(1/2)*x) maximaal 48 is, dan is x minimaal -36.
Als (30-(1/2)*x) maximaal 0 is, dan is x minimaal 60.
Omdat het een lineaire vergelijking is kunnen we concluderen dat het minimum van x tussen de -36 en 60 ligt, afhankelijk van wat het echte maximum van 30-(1/2)*x is.
Als (30-(1/2)*x) maximaal 0 is, dan is x minimaal 60.
Omdat het een lineaire vergelijking is kunnen we concluderen dat het minimum van x tussen de -36 en 60 ligt, afhankelijk van wat het echte maximum van 30-(1/2)*x is.
Weet iemand of een BHI (betrouwbaarheidsinterval) alleen wordt gebruikt voor populatie? Dus dat je altijd met z* waardes rekent of is het ook mogelijk een BHI voor een steekproef te maken en dan dus met t* waardes rekenen ?
Same shit different day
Wat is een BHI voor een populatie of steekproef? Ik ken alleen BHI's voor (functies van) parameters van een kansverdeling.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Hoe bepaal ik de afgeleide van U=AB² = (1000-S)•(1050+1.05S)²? Ik kom er echt niet uit. Het antwoord zou ∂U/∂S = 1'102'500-2205S-1323S²/400 moeten zijn.
Je kunt dit op twee manieren aanpakken:quote:
Hoe bepaal ik de afgeleide van U=AB² = (1000-S)•(1050+1.05S)²? Ik kom er echt niet uit. Het antwoord zou ∂U/∂S = 1'102'500-2205S-1323S²/400 moeten zijn.
1. De haakjes uitwerken en dan de bekende regels voor het differentiëren van een polynoom toepassen (i.e term voor term de regels voor het differentiëren van een macht toepassen).
2. De haakjes laten staan en werken met een combinatie van de productregel en de kettingregel.
A fair coin is thrown n times, let Y be the amount of throws required before observing one "heads".
Given µ = 2 and s^2=2 calculate the upper bound W (amount of throws) with a probability of 0.95.
Chebyshev's inequality geeft P[(µ-ks)<Y<(µ+ks)]>=1-1/k^2
We willen P=0.95 dus 1-1/k^2=0.95 ... 1/k^2=0.05 dus k=2sqrt5
Dan is de upper bound µ+ks = 2+2sqrt5*sqrt2 = 2+2sqrt10 ?
Given µ = 2 and s^2=2 calculate the upper bound W (amount of throws) with a probability of 0.95.
Chebyshev's inequality geeft P[(µ-ks)<Y<(µ+ks)]>=1-1/k^2
We willen P=0.95 dus 1-1/k^2=0.95 ... 1/k^2=0.05 dus k=2sqrt5
Dan is de upper bound µ+ks = 2+2sqrt5*sqrt2 = 2+2sqrt10 ?
Misschien kun je een krappere bovengrens vinden met de negatieve binomiale verdeling.
En als je n keer gooit, weet je toch niet zeker dat je een keer kop gooit?
En als je n keer gooit, weet je toch niet zeker dat je een keer kop gooit?
Maak gewoon een tabelletje met de cdf.
En hier is de geometrische verdeling simpeler.
En hier is de geometrische verdeling simpeler.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Rare vraag idd, zo zou Y niet gedefinieerd hoeven zijn.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik moet het met chebyshev doen, inleveropdrachtje....
Er zat namelijk nog een vraag aan vast die ik ook moest oplossen.
Dat heb ik er van gemaakt, er staat niet n times, maar gewoon dat hij gegooid wordt totdat er een keer kop valt.quote:
Maar waar slaat dan 'A fair coin is thrown n times' op?
Er zat namelijk nog een vraag aan vast die ik ook moest oplossen.
Je kunt nog gebruiken dat het antwoord een natuurlijk getal is.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dat ik daar zelf niet aan gedacht heb, stom stom stom.quote:
Je kunt nog gebruiken dat het antwoord een natuurlijk getal is.
Waarom is er maar één afbeelding van de lege verzameling naar een willekeurige verzameling B?
Hetzelfde voor alle afbeeldingen van de lege verzameling naar de lege verzameling, waarom is dat maar één afbeelding?
Hetzelfde voor alle afbeeldingen van de lege verzameling naar de lege verzameling, waarom is dat maar één afbeelding?
Als het er meer waren, dan zou er een element in de lege verzameling moeten zijn dat naar verschillende elementen van B wordt gestuurd. Aangezien de lege verzameling geen elementen heeft, gaat dat niet.
Waarom kan ik het niet zo bekijken:
Neem een afbeelding van de lege verzameling naar een willekeurige verzameling B. Dan beeldt die afbeelding alle elementen van de lege verzameling af op B. Aangezien er geen elementen zijn, maakt het niet uit hoe je die elementen afbeeldt want je zit dan toch in B.
Dus kan je elke afbeelding hiervoor gebruiken.
Neem een afbeelding van de lege verzameling naar een willekeurige verzameling B. Dan beeldt die afbeelding alle elementen van de lege verzameling af op B. Aangezien er geen elementen zijn, maakt het niet uit hoe je die elementen afbeeldt want je zit dan toch in B.
Dus kan je elke afbeelding hiervoor gebruiken.
Sterker nog, je beeldt helemaal niks af. Je komt dus eigenlijk nooit in B, loosely speaking.quote:
Waarom kan ik het niet zo bekijken:
Neem een afbeelding van de lege verzameling naar een willekeurige verzameling B. Dan beeldt die afbeelding alle elementen van de lege verzameling af op B. Aangezien er geen elementen zijn, maakt het niet uit hoe je die elementen afbeeldt want je zit dan toch in B.
Dus kan je elke afbeelding hiervoor gebruiken.
Ik zou het zo zeggen:
Een functie f1: emptyset --> B is gelijk aan f2: emptyset -->B d.e.s.d.a. f1(a)=f2(a) voor iedere a in de lege verzameling. Omdat er geen a in de lege verzameling zit is dit triviaal waar. Omdat we geen verdere aannames over f1 en f2 hebben gemaakt geldt voor alle functies van de lege verzameling naar B dat ze gelijk zijn aan elkaar.
Hmm, en hoe maak je dan duidelijk dat er een afbeelding is van de lege verzameling naar B?
Er wordt immers niks afgebeeld, is dat dan gelijk aan de lege afbeelding en dus zit die afbeeling in B?
Er wordt immers niks afgebeeld, is dat dan gelijk aan de lege afbeelding en dus zit die afbeeling in B?
Je ziet het makkelijker met de definitie van een functie als geordend drietal verzamelingen: http://nl.wikipedia.org/wiki/Functie_%28wiskunde%29#Definitie
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Is niet eens nodig toch? Een functie f: X-->Y is een object dat aan iedere x in X een unieke f(x) = y in Y toevoegt. Opnieuw triviaal waar dat zo'n f bestaat met X de lege verzameling.
Het is net zo'n soort uitspraak als "ik geef ieder marsmannetje een (uniek) koekje".Omdat ze niet bestaan ("de verzameling marsmannetjes is leeg"), is het automatisch waar.
Het is net zo'n soort uitspraak als "ik geef ieder marsmannetje een (uniek) koekje".Omdat ze niet bestaan ("de verzameling marsmannetjes is leeg"), is het automatisch waar.
Klopt het dan als ik zeg:
Van de lege verzameling naar een willekeurige verzameling is er een afbeelding omdat je alle elementen kunt afbeelden op het codomein. Dus er is een afbeelding f . Stel dat er nog een afbeelding g is, dan geld, voor alle a uit het lege domein, g(a)=f(a) omdat er geen a in het lege domein zijn. Dus is er maar één unieke afbeelding.
Of
Je hebt een functie omdat ('lege verzameling', B, {x,f(x):x in de lege verzameling}) bestaat en voor een andere 'f' krijg je dezelfde verzameling: {x,f(x): x in lege verzameling} = {x,g(x) : x in lege verzameling} , dus
('lege verzameling', B, {x,f(x):x in de lege verzameling}) = ('lege verzameling', B, {x,g(x):x in de lege verzameling}) .
Van de lege verzameling naar een willekeurige verzameling is er een afbeelding omdat je alle elementen kunt afbeelden op het codomein. Dus er is een afbeelding f . Stel dat er nog een afbeelding g is, dan geld, voor alle a uit het lege domein, g(a)=f(a) omdat er geen a in het lege domein zijn. Dus is er maar één unieke afbeelding.
Of
Je hebt een functie omdat ('lege verzameling', B, {x,f(x):x in de lege verzameling}) bestaat en voor een andere 'f' krijg je dezelfde verzameling: {x,f(x): x in lege verzameling} = {x,g(x) : x in lege verzameling} , dus
('lege verzameling', B, {x,f(x):x in de lege verzameling}) = ('lege verzameling', B, {x,g(x):x in de lege verzameling}) .
Ik prefereer de eerste versie maar ze zijn beide goed.
-------------------------
Weet iemand wat P > |t| betekent in de statistiek? (ik denk dat de t op de "t-statistic" slaat en de p op de "p-value", maar de bijbehorende output is dan bijvoorbeeld 0.000. Hoe moet je dat dan interpreteren?)
-------------------------
Weet iemand wat P > |t| betekent in de statistiek? (ik denk dat de t op de "t-statistic" slaat en de p op de "p-value", maar de bijbehorende output is dan bijvoorbeeld 0.000. Hoe moet je dat dan interpreteren?)
x,f(x) moet zijn (x,f(x)), of het derde ding moet gewoon {} zijn. De enige functie is dus ({}, B, {}).
Bedoel je niet P(T > |t|) met T een t-verdeelde stochast, en t de t-statistic?quote:
Ik prefereer de eerste versie maar ze zijn beide goed.
-------------------------
Weet iemand wat P > |t| betekent in de statistiek? (ik denk dat de t op de "t-statistic" slaat en de p op de "p-value", maar de bijbehorende output is dan bijvoorbeeld 0.000. Hoe moet je dat dan interpreteren?)
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Waarom is de afgeleide van een constant getal 0? Stel je hebt 5 (waar dus eigenlijk staat 5^1 toch?). Als je dan de afgeleide neemt wordt dan 1x5^0 = 1?
Waarom is de afgeleide van 5x gelijk aan 5? Stel je hebt 5x (waar dus eigenlijk staat 5^1x^1 toch?). Als je dan de afgeleide neemt wordt dat met de productregel 1*5^0 x + 5*1*x^0 = 1*x+5 = 5+x.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
De afgeleide in een lineaire vergelijking kan je opvatten als de helling (richtingscoëfficiënt) van de lijn. Wat is de helling van de lijn y=5 ?quote:Op zondag 2 oktober 2011 14:24 schreef Burbujas het volgende:
Waarom is de afgeleide van een constant getal 0? Stel je hebt 5 (waar dus eigenlijk staat 5^1 toch?). Als je dan de afgeleide neemt wordt dan 1x5^0 = 1?
Ik dacht ook dat ze zoiets bedoelen, maar in die tabellen staat toch echt P > |t| . Ze verwerpen H0 als de P > |t| waarde kleiner is dan het significantieniveau, dus dan zal dat wel.quote:
Bedoel je niet P(T > |t|) met T een t-verdeelde stochast, en t de t-statistic?
enig idee wat afgeleide wil zeggen? wat je daarmee berekent?quote:
Waarom is de afgeleide van een constant getal 0? Stel je hebt 5 (waar dus eigenlijk staat 5^1 toch?). Als je dan de afgeleide neemt wordt dan 1x5^0 = 1?
edit: oh iemand was me al voor
~Si vis amari, ama~
Mijn 2 centjes:quote:
Waarom is de afgeleide van een constant getal 0? Stel je hebt 5 (waar dus eigenlijk staat 5^1 toch?). Als je dan de afgeleide neemt wordt dan 1x5^0 = 1?
De afgeleide van een functie f(x) in het punt x is gedefinieerd als
Voor een constante functie f(x) = C, waarbij C staat voor "constante", geldt in elk punt x
Mag jij er een plaatje bij tekenen en kijken of je het ook meetkundig begrijpt
Kijk ook es of je met deze definitie de afgeleide van een functie als f(x) = ax+b kunt berekenen.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Hier heb ik wat aan, dank je wel.quote:
[..]
Mijn 2 centjes:
De afgeleide van een functie f(x) in het punt x is gedefinieerd als
Voor een constante functie f(x) = C, waarbij C staat voor "constante", geldt in elk punt x
Mag jij er een plaatje bij tekenen en kijken of je het ook meetkundig begrijpt
Ik snap best dat de helling van een rechte lijn nul is, maar was op zoek naar het bewijs hiervoor.quote:Op zondag 2 oktober 2011 14:29 schreef FedExpress het volgende:
[..]
enig idee wat afgeleide wil zeggen? wat je daarmee berekent?
edit: oh iemand was me al voor
Probeer wat Haushofer deed ook eens met f(x) = a x + b, dan snap je waarom de afgeleide van een lineaire vergelijking gelijk is aan a.quote:Op zondag 2 oktober 2011 14:47 schreef Burbujas het volgende:
[..]
Ik snap best dat de helling van een rechte lijn nul is, maar was op zoek naar het bewijs hiervoor.
Oh wacht dat zei die zelf al
Dan moet er bij die tabel een toelichting staan, want het is geen standaardnotatie.quote:
[..]
Ik dacht ook dat ze zoiets bedoelen, maar in die tabellen staat toch echt P > |t| . Ze verwerpen H0 als de P > |t| waarde kleiner is dan het significantieniveau, dus dan zal dat wel.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Het is de output van een statistiekprogramma. Ik moet daar opeens mee werken zonder dat ik er eerst uitleg over heb gehad. Andere studenten hebben er al eerder mee gewerkt dus toen zal het wel aan bod zijn gekomenquote:
[..]
Dan moet er bij die tabel een toelichting staan, want het is geen standaardnotatie.
.quote:
Nog bedankt voor de uitleg over afbeeldingen!
Vraag: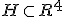
het hypervlak met normal a = (1,-1,1,-1) gaat door het punt q = (1,2,-1,-2). Bepaal de afstand tussen punt p = (2,1,-3,1) tot H.
Voor elementen in H geldt <a,x> = b. q invullen geeft <a,q> = 0 dus b = 0.
De normaal a staat dus loodrecht op H. En dan is het een kwestie van uitrekenen.
Klopt het wat ik zeg? Iemand anders beweert dat ik overal q vanaf moet trekken, maar omdat <a,q> = 0 denk ik van niet.
Voor elementen in H geldt <a,x> = b. q invullen geeft <a,q> = 0 dus b = 0.
De normaal a staat dus loodrecht op H. En dan is het een kwestie van uitrekenen.
Klopt het wat ik zeg? Iemand anders beweert dat ik overal q vanaf moet trekken, maar omdat <a,q> = 0 denk ik van niet.
De vergelijking van het hypervlak is inderdaad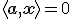 
. Dus als je dan 
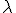keer de normaalvector bij 
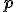optelt kom je uit in het hypervlak. Ik denk dus dat
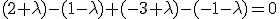
dus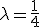
, en dan krijg je de afstand 
.
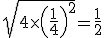dus
Behalve dan dat de laatste van je optelling 1 is en niet -1, toch? Ik kreeg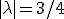 
, dus afstand is 3/2. Bedankt.
Integreer sqrtx/(1+x) van 0 tot 1
Eerst substituren van y = sqrtx dus x = y² dan wordt dx = 2ydy
Krijg je 2* integraal y²/(y²+1) van 0 tot 1 (grenzen blijven hetzelfde..). Nu heb ik een beetje een "en nu?" gevoel. Ik heb geprobeerd simpelweg de quotiëntregel uit te voeren maar dan krijg ik een antwoord dat niet klopt...
ps: kan het wel oplossen mbv een methode uit wolfram, maar die hoor ik nog niet te kennen..
[ Bericht 13% gewijzigd door Physics op 03-10-2011 12:15:09 ]
Eerst substituren van y = sqrtx dus x = y² dan wordt dx = 2ydy
Krijg je 2* integraal y²/(y²+1) van 0 tot 1 (grenzen blijven hetzelfde..). Nu heb ik een beetje een "en nu?" gevoel. Ik heb geprobeerd simpelweg de quotiëntregel uit te voeren maar dan krijg ik een antwoord dat niet klopt...
ps: kan het wel oplossen mbv een methode uit wolfram, maar die hoor ik nog niet te kennen..
[ Bericht 13% gewijzigd door Physics op 03-10-2011 12:15:09 ]
y2/(y2 + 1) = ((y2 + 1) - 1)/(y2 + 1) = 1 - 1/(y2 + 1).quote:
Integreer sqrtx/(1+x) van 0 tot 1
Eerst substituren van y = sqrtx dus x = y² dan wordt dx = 2ydy
Krijg je 2* integraal y²/(y²+1) van 0 tot 1 (grenzen blijven hetzelfde..). Nu heb ik een beetje een "en nu?" gevoel. Ik heb geprobeerd simpelweg de quotiëntregel uit te voeren maar dan krijg ik een antwoord dat niet klopt...
ps: kan het wel oplossen mbv een methode uit wolfram, maar die hoor ik nog niet te kennen..
Yes, arctan yquote:
Oh dat klinkt ook logisch, ik had het met een staartdeling gedaan.quote:
[..]
y2/(y2 + 1) = ((y2 + 1) - 1)/(y2 + 1) = 1 - 1/(y2 + 1).
Hallo, ik kom uit deze oefenopgave niet uit:
De baan van een bewegend deeltje wordt beschreven door:
R(t) = <3t, 4 sin (t) , 4 cos (t)> Gegeven zijn de punten P(0,0,4) en Q(7,5 pi,4,0)
Bewijs dat de kromming in elk punt van de baan even groot is.
Hoe pak je dit aan ? Ik dacht zelf aan:
cos (x) = P . Q (inproduct)/ |P| . |Q|
|P| = 4
|Q| = 9.48
Aangezien het inproduct van PQ gelijk is aan 0 onstaat er: cos (x) = 0/ 37,92. Hieruit volgt dat x gelijk is aan 90 graden en dus voor ieder punt op de kromme gelijk is. Is deze redenatie juist ?
De baan van een bewegend deeltje wordt beschreven door:
R(t) = <3t, 4 sin (t) , 4 cos (t)> Gegeven zijn de punten P(0,0,4) en Q(7,5 pi,4,0)
Bewijs dat de kromming in elk punt van de baan even groot is.
Hoe pak je dit aan ? Ik dacht zelf aan:
cos (x) = P . Q (inproduct)/ |P| . |Q|
|P| = 4
|Q| = 9.48
Aangezien het inproduct van PQ gelijk is aan 0 onstaat er: cos (x) = 0/ 37,92. Hieruit volgt dat x gelijk is aan 90 graden en dus voor ieder punt op de kromme gelijk is. Is deze redenatie juist ?
Een kromming is toch geen hoek? Waarom gebruik je zomaar twee punten P en Q om voor de hele baan iets te bewijzen?
dus ik moet eerst de lengte van de kromme tussen P en Q bepalen ? Volgens mij is dit gelijk aan de wortel van (7.5 pi - 0)^2 + (4-0)^2 + (0 - 4) 2 = wortel 56.24 pi^2 + 32. Hoe kan ik de hoek op een kromme op een willekeurig punt definieren ?
Dat is niet de lengte van de kromme tussen P en Q. Je berekent daar gewoon de afstand tussen P en Q. De kromme loopt niet recht tussen P en Q. Je zou de afstand kunnen berekenen door de integraal
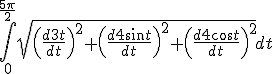
Maar dat heeft volgens mij niets met kromming te maken. De kromming is de lengte van de tweede afgeleide.
Maar dat heeft volgens mij niets met kromming te maken. De kromming is de lengte van de tweede afgeleide.
