[Bèta wiskunde] Huiswerk- en vragentopic

zondag 2 oktober 2011 @ 14:24:15 #276

Burbujas

Waarom is de afgeleide van een constant getal 0? Stel je hebt 5 (waar dus eigenlijk staat 5^1 toch?). Als je dan de afgeleide neemt wordt dan 1x5^0 = 1?

zondag 2 oktober 2011 @ 14:26:01 #277

GlowMouse

l'état, c'est moi

Waarom is de afgeleide van 5x gelijk aan 5? Stel je hebt 5x (waar dus eigenlijk staat 5^1x^1 toch?). Als je dan de afgeleide neemt wordt dat met de productregel 1*5^0 x + 5*1*x^0 = 1*x+5 = 5+x.

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

zondag 2 oktober 2011 @ 14:27:23 #278

thenxero

quote:
Op zondag 2 oktober 2011 14:24 schreef Burbujas het volgende:
Waarom is de afgeleide van een constant getal 0? Stel je hebt 5 (waar dus eigenlijk staat 5^1 toch?). Als je dan de afgeleide neemt wordt dan 1x5^0 = 1?

De afgeleide in een lineaire vergelijking kan je opvatten als de helling (richtingscoëfficiënt) van de lijn. Wat is de helling van de lijn y=5 ?

zondag 2 oktober 2011 @ 14:29:25 #279

thenxero

quote:
Op zondag 2 oktober 2011 14:13 schreef GlowMouse het volgende:
Bedoel je niet P(T > |t|) met T een t-verdeelde stochast, en t de t-statistic?

Ik dacht ook dat ze zoiets bedoelen, maar in die tabellen staat toch echt P > |t| . Ze verwerpen H₀ als de P > |t| waarde kleiner is dan het significantieniveau, dus dan zal dat wel.

zondag 2 oktober 2011 @ 14:29:49 #280

FedExpress

quote:
Op zondag 2 oktober 2011 14:24 schreef Burbujas het volgende:
Waarom is de afgeleide van een constant getal 0? Stel je hebt 5 (waar dus eigenlijk staat 5^1 toch?). Als je dan de afgeleide neemt wordt dan 1x5^0 = 1?

enig idee wat afgeleide wil zeggen? wat je daarmee berekent?

edit: oh iemand was me al voor

~Si vis amari, ama~

zondag 2 oktober 2011 @ 14:34:54 #281

Haushofer

quote:
Op zondag 2 oktober 2011 14:24 schreef Burbujas het volgende:
Waarom is de afgeleide van een constant getal 0? Stel je hebt 5 (waar dus eigenlijk staat 5^1 toch?). Als je dan de afgeleide neemt wordt dan 1x5^0 = 1?

Mijn 2 centjes:

De afgeleide van een functie f(x) in het punt x is gedefinieerd als

$\frac{df}{dx}(x) \equiv \lim_{\Delta x \rightarrow 0}\frac{f(x+\Delta x) - f(x)}{\Delta x}$

Voor een constante functie f(x) = C, waarbij C staat voor "constante", geldt in elk punt x

$\frac{df}{dx}(x) \equiv \lim_{\Delta x \rightarrow 0}\frac{C- C}{\Delta x} = 0$

Mag jij er een plaatje bij tekenen en kijken of je het ook meetkundig begrijpt

Kijk ook es of je met deze definitie de afgeleide van een functie als f(x) = ax+b kunt berekenen.

-

zondag 2 oktober 2011 @ 14:46:55 #282

Burbujas

quote:
Op zondag 2 oktober 2011 14:34 schreef Haushofer het volgende:

[..]

Mijn 2 centjes:

De afgeleide van een functie f(x) in het punt x is gedefinieerd als

$\frac{df}{dx}(x) \equiv \lim_{\Delta x \rightarrow 0}\frac{f(x+\Delta x) - f(x)}{\Delta x}$

Voor een constante functie f(x) = C, waarbij C staat voor "constante", geldt in elk punt x

$\frac{df}{dx}(x) \equiv \lim_{\Delta x \rightarrow 0}\frac{C- C}{\Delta x} = 0$

Mag jij er een plaatje bij tekenen en kijken of je het ook meetkundig begrijpt Kijk ook es of je met deze definitie de afgeleide van een functie als f(x) = ax+b kunt berekenen.

Hier heb ik wat aan, dank je wel.

zondag 2 oktober 2011 @ 14:47:57 #283

Burbujas

quote:
Op zondag 2 oktober 2011 14:29 schreef FedExpress het volgende:

[..]

enig idee wat afgeleide wil zeggen? wat je daarmee berekent?

edit: oh iemand was me al voor

Ik snap best dat de helling van een rechte lijn nul is, maar was op zoek naar het bewijs hiervoor.

zondag 2 oktober 2011 @ 14:56:10 #284

thenxero

quote:
Op zondag 2 oktober 2011 14:47 schreef Burbujas het volgende:

[..]

Ik snap best dat de helling van een rechte lijn nul is, maar was op zoek naar het bewijs hiervoor.

Probeer wat Haushofer deed ook eens met f(x) = a x + b, dan snap je waarom de afgeleide van een lineaire vergelijking gelijk is aan a.
Oh wacht dat zei die zelf al

zondag 2 oktober 2011 @ 14:57:53 #285

GlowMouse

l'état, c'est moi

quote:
Op zondag 2 oktober 2011 14:29 schreef thenxero het volgende:

[..]

Ik dacht ook dat ze zoiets bedoelen, maar in die tabellen staat toch echt P > |t| . Ze verwerpen H₀ als de P > |t| waarde kleiner is dan het significantieniveau, dus dan zal dat wel.

Dan moet er bij die tabel een toelichting staan, want het is geen standaardnotatie.

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

zondag 2 oktober 2011 @ 14:59:32 #286

Siddartha

Nog bedankt voor de uitleg over afbeeldingen!

zondag 2 oktober 2011 @ 15:00:41 #287

thenxero

quote:
Op zondag 2 oktober 2011 14:57 schreef GlowMouse het volgende:

[..]

Dan moet er bij die tabel een toelichting staan, want het is geen standaardnotatie.

Het is de output van een statistiekprogramma. Ik moet daar opeens mee werken zonder dat ik er eerst uitleg over heb gehad. Andere studenten hebben er al eerder mee gewerkt dus toen zal het wel aan bod zijn gekomen

.

quote:
Op zondag 2 oktober 2011 14:59 schreef Siddartha het volgende:
Nog bedankt voor de uitleg over afbeeldingen!

zondag 2 oktober 2011 @ 17:15:47 #288

Anoonumos

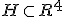Vraag: $H \subset R^{4}$ het hypervlak met normal a = (1,-1,1,-1) gaat door het punt q = (1,2,-1,-2). Bepaal de afstand tussen punt p = (2,1,-3,1) tot H.

Voor elementen in H geldt <a,x> = b. q invullen geeft <a,q> = 0 dus b = 0.
De normaal a staat dus loodrecht op H. En dan is het een kwestie van uitrekenen.

Klopt het wat ik zeg? Iemand anders beweert dat ik overal q vanaf moet trekken, maar omdat <a,q> = 0 denk ik van niet.

zondag 2 oktober 2011 @ 18:08:26 #289

twaalf

De vergelijking van het hypervlak is inderdaad 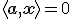$\langle\mathbf{a},\mathbf{x}\rangle=0$ . Dus als je dan 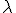$\lambda$ keer de normaalvector bij 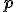$\mathbf{p}$ optelt kom je uit in het hypervlak. Ik denk dus dat
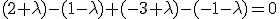
$(2+\lambda)-(1-\lambda)+(-3+\lambda)-(-1-\lambda)=0$
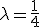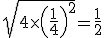dus $\lambda=\frac{1}{4}$ , en dan krijg je de afstand $\sqrt{4\times\left(\frac{1}{4}\right)^2}=\frac{1}{2}$ .

zondag 2 oktober 2011 @ 18:20:07 #290

Anoonumos

Behalve dan dat de laatste van je optelling 1 is en niet -1, toch? Ik kreeg 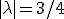$|\lambda| = 3/4$ , dus afstand is 3/2. Bedankt.

zondag 2 oktober 2011 @ 18:26:39 #291

twaalf

Klopt.

maandag 3 oktober 2011 @ 12:09:37 #292

Physics

Integreer sqrtx/(1+x) van 0 tot 1

Eerst substituren van y = sqrtx dus x = y² dan wordt dx = 2ydy

Krijg je 2* integraal y²/(y²+1) van 0 tot 1 (grenzen blijven hetzelfde..). Nu heb ik een beetje een "en nu?" gevoel. Ik heb geprobeerd simpelweg de quotiëntregel uit te voeren maar dan krijg ik een antwoord dat niet klopt...

ps: kan het wel oplossen mbv een methode uit wolfram, maar die hoor ik nog niet te kennen..

[ Bericht 13% gewijzigd door Physics op 03-10-2011 12:15:09 ]

maandag 3 oktober 2011 @ 12:38:18 #293

GlowMouse

l'état, c'est moi

Kun je 1/(y²+1) wel primitiveren?

eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0

maandag 3 oktober 2011 @ 12:51:46 #294

Riparius

quote:
Op maandag 3 oktober 2011 12:09 schreef Physics het volgende:
Integreer sqrtx/(1+x) van 0 tot 1

Eerst substituren van y = sqrtx dus x = y² dan wordt dx = 2ydy

Krijg je 2* integraal y²/(y²+1) van 0 tot 1 (grenzen blijven hetzelfde..). Nu heb ik een beetje een "en nu?" gevoel. Ik heb geprobeerd simpelweg de quotiëntregel uit te voeren maar dan krijg ik een antwoord dat niet klopt...

ps: kan het wel oplossen mbv een methode uit wolfram, maar die hoor ik nog niet te kennen..

y²/(y² + 1) = ((y² + 1) - 1)/(y² + 1) = 1 - 1/(y² + 1).

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

maandag 3 oktober 2011 @ 22:52:21 #295

Physics

quote:
Op maandag 3 oktober 2011 12:38 schreef GlowMouse het volgende:
Kun je 1/(y²+1) wel primitiveren?

Yes, arctan y

quote:
Op maandag 3 oktober 2011 12:51 schreef Riparius het volgende:

[..]

y²/(y² + 1) = ((y² + 1) - 1)/(y² + 1) = 1 - 1/(y² + 1).

Oh dat klinkt ook logisch, ik had het met een staartdeling gedaan.

dinsdag 4 oktober 2011 @ 18:26:58 #296

derekiej

Hallo, ik kom uit deze oefenopgave niet uit:

De baan van een bewegend deeltje wordt beschreven door:

R(t) = <3t, 4 sin (t) , 4 cos (t)> Gegeven zijn de punten P(0,0,4) en Q(7,5 pi,4,0)

Bewijs dat de kromming in elk punt van de baan even groot is.

Hoe pak je dit aan ? Ik dacht zelf aan:

cos (x) = P . Q (inproduct)/ |P| . |Q|

|P| = 4
|Q| = 9.48

Aangezien het inproduct van PQ gelijk is aan 0 onstaat er: cos (x) = 0/ 37,92. Hieruit volgt dat x gelijk is aan 90 graden en dus voor ieder punt op de kromme gelijk is. Is deze redenatie juist ?

dinsdag 4 oktober 2011 @ 18:42:27 #297

twaalf

Een kromming is toch geen hoek? Waarom gebruik je zomaar twee punten P en Q om voor de hele baan iets te bewijzen?

dinsdag 4 oktober 2011 @ 18:56:41 #298

derekiej

dus ik moet eerst de lengte van de kromme tussen P en Q bepalen ? Volgens mij is dit gelijk aan de wortel van (7.5 pi - 0)^2 + (4-0)^2 + (0 - 4) 2 = wortel 56.24 pi^2 + 32. Hoe kan ik de hoek op een kromme op een willekeurig punt definieren ?

dinsdag 4 oktober 2011 @ 19:06:59 #299

twaalf

Dat is niet de lengte van de kromme tussen P en Q. Je berekent daar gewoon de afstand tussen P en Q. De kromme loopt niet recht tussen P en Q. Je zou de afstand kunnen berekenen door de integraal
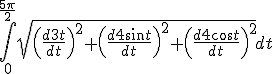
$\int_0^{\frac{5\pi}{2}}\sqrt{\left(\frac{d3t}{dt}\right)^2+\left(\frac{d4\sin t}{dt}\right)^2+\left(\frac{d4\cos t}{dt}\right)^2}dt$
Maar dat heeft volgens mij niets met kromming te maken. De kromming is de lengte van de tweede afgeleide.

dinsdag 4 oktober 2011 @ 19:07:47 #300

derekiej

volgens mij heb ik nu de lengte van het lijnstuk PQ berekend en niet die van de kromme.

Forum Opties
Forumhop:
Hop naar:	(afkorting, bv 'KLB')

» school, studie en onderwijs

» school, studie en onderwijs