[Beta] huiswerk en vragen topic

quote:

Op zondag 26 augustus 2007 14:40 schreef Iblis het volgende:

SPOILER

Om spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.

SPOILER

Om spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.

Waarom telkens die irritante spoilers?

idd

Hulp nodig met wiskunde:

De functie g(x) is gegeven door: g(x) = 3e-machtswortel uit x+1

i) bepaal de tweede orde Taylorreeksonwikkeling rond x = 0
ii) laat zien dat |R3(x)|< 5x^3 / 81
iii) Bepaal de 3e-machtswortel uit 1003

En nog een over limieten:

Bepaal de volgende limiet:

Lim x-> oneindig ln(x) / x

Dank u vriendelijk.

quote:

Op maandag 27 augustus 2007 10:15 schreef KaterPils het volgende:
Hulp nodig met wiskunde:

De functie g(x) is gegeven door: g(x) = 3e-machtswortel uit x+1

i) bepaal de tweede orde Taylorreeksonwikkeling rond x = 0
ii) laat zien dat |R3(x)|< 5x^3 / 81
iii) Bepaal de 3e-machtswortel uit 1003

En nog een over limieten:

Bepaal de volgende limiet:

Lim x-> oneindig ln(x) / x

Dank u vriendelijk.

Weet je wel wat een Taylorreeks is? Als je de definituie bekijkt, kun je de ontwikkeling toch gewoon uitschrijven? De restterm schatten is heel eenvoudig. Kom, iets meer eigen initiatief , probeer het eerst even zelf en geef dan aan waar je vastloopt.

quote:

Op dinsdag 28 augustus 2007 22:59 schreef GlowMouse het volgende:
Mogen er in een samenhangende ongerichte graaf twee kanten zijn tussen twee knopen?

Nee. Een ongerichte graaf is een paar verzamelingen (V,E) waarbij de elementen van E ongeordende paren van verschillende elementen van V zijn. Deze definitie laat niet toe dat er twee kanten tussen twee knopen lopen.

[ Bericht 2% gewijzigd door thabit op 29-08-2007 17:48:21 ]

Even een hele simpele:

Corrinne travels from home to work at an average speed of 50 miles per hour, and returns home by the same route at 60 miles per hour. It takes her 10 more minutes to get to work than it takes her to get home. How many miles is it from Corinne's home to work?

A 25
B 35
C 50
D 75
E 90

Het antwoord is C. Hoe kun je daar komen zonder alle oplossingen na te rekenen?

Gewoon uitproberen en dan zie je dat het 50 miles is.
Heenweg is dan 1 uur.
Terugweg is dan 50 minuten (60 m/uur --> 10 m/10 min --> 50 m / 50 min)
En dan is ze dus 10 min sneller.

-edit-
ah, en nu wil je het zonder allemaal uit te rekenen.
Het is me wat

-edit-edit-

Stel x = afstand.
Heenweg duurt dan x / 50 in uren
Terugweg duurt dan x / 60 in uren
Dan geldt er: x / 50 - x / 60 = verschil in tijd tussen heenweg en terugweg.
Herschrijven levert op: 6x/300 - 5x/300= x/ 300
Dat antwoord moet hetzelfde zijn als 10 minuten, oftewel 1/6 uur
Dat kan alleen als x 1/6 deel is van 300, en dus 50 mile.
Want 50/300 = 1/6

[ Bericht 24% gewijzigd door -J-D- op 29-08-2007 16:34:11 ]

Danku!

quote:

Op zondag 26 augustus 2007 10:47 schreef Wolfje het volgende:
De koning heeft inderdaad 10 slaven nodig .

Nu een vraagje over algoritmen!

Gegeven n haaien waarvan de kracht, snelheid en intelligentie (dit zijn constanten) bekend zijn. Een haai kan een andere haai opeten als hij minstens net zo sterk, snel en slim is. Voorts is gegeven dat een haai maximaal 2 andere haaien kan opeten. Geef een algoritme om het kleinst aantal haaien dat na de lunch nog in leven is, te bepalen .

Ik vermoed dat er een voorwaarde m.b.t. timing mist? Kan een haai die al een andere haai gegeten heeft nu wel of niet opgegeten worden door nog een andere haai? Logisch gezien kan een haai natuurlijk niet tegelijkertijd twee haaien eten, dus zou een haai zowel eter als prooi moeten kunnen zijn. Dit zie ik echter niet terug in de aangedragen oplossingen?

Stel je hebt de haaien (1,1,2), (1,2,1), (2,1,1), (1,1,3), (1,2,3) en (3,3,3). Volgens de voorwaarden is het zelfs mogelijk dat (1,1,3) (1,1,2) opeet en dat vervolgens (1,2,3) (1,2,1) en (1,1,3) opeet en weer vervolgens dat (3,3,3) (2,1,1) en (1,2,3) opeet.

quote:

Op zondag 2 september 2007 02:54 schreef cjs het volgende:

[..]

Ik vermoed dat er een voorwaarde m.b.t. timing mist? Kan een haai die al een andere haai gegeten heeft nu wel of niet opgegeten worden door nog een andere haai?

quote:

Op zondag 26 augustus 2007 12:43 schreef Wolfje het volgende:
En ze kunnen elkaar ook niet tegelijkertijd op eten .

Waaruit ik zou afleiden dat een haai zeker niet postuum nog een andere haai kan eten.

quote:

Logisch gezien kan een haai natuurlijk niet tegelijkertijd twee haaien eten, dus zou een haai zowel eter als prooi moeten kunnen zijn. Dit zie ik echter niet terug in de aangedragen oplossingen?

Jawel, mijn oplossing houdt daar impiliciet met de manier van coderen van de bipartiete graaf rekening mee.

quote:

Stel je hebt de haaien (1,1,2), (1,2,1), (2,1,1), (1,1,3), (1,2,3) en (3,3,3). Volgens de voorwaarden is het zelfs mogelijk dat (1,1,3) (1,1,2) opeet en dat vervolgens (1,2,3) (1,2,1) en (1,1,3) opeet en weer vervolgens dat (3,3,3) (2,1,1) en (1,2,3) opeet.

We kunnen een partiële ordening op jouw haaien aanbrengen, van klein naar groot:

[ (1, 1, 2), (1,2,1) (2, 1, 1) ] ; [ (1, 1, 3) ] ; [(1,2,3) ] ; [(3,3,3)]

De haaien in een 'blok' (tussen [ ]) kunnen elkaar niet opeten, maar ze kunnen wel opgegeten worden door alle haaien in een blok 'rechts' ervan. De lunch moet dus beginnen doordat in het eerste 'tijdsmoment' alleen haaien uit het kleinste blok gegeten worden. Het volgende moment mogen alle haaien uit het blok erna gegeten worden, et cetera. Dat levert de optimale haaiconsumptie op. De vraag is namelijk wat is het “kleinste aantal dat over is”, en daarvoor ga je van deze optimale consumptie uit.

Er is alleen één valkuil, namelijk gelijke haaien (b.v. (1,1,1) en (1,1,1) ). Want die zitten in hetzelfde blok, maar kunnen elkaar eventueel opeten. Dat is niet mogelijk, bij het coderen van de graaf wordt zo'n cykel arbitrair doorbroken door een willekeurige ordening onder deze haaien aan te brengen, zodat er geen cyklische afhankelijkheden ontstaan.

Hmm, ik moet eens beter lezen, ookal is het 's nachts.

Ik ging eerst hier vanuit:

quote:

Op zondag 26 augustus 2007 11:49 schreef Iblis het volgende:

[..]


Drie haaien: (1,1,2), (1,2,1) en (2,1,1): Deze kunnen elkaar niet opeten.

Nog drie haaien: (1,1,3), (3,3,3) en (3,1,1): Deze kunnen elkaar niet opeten. (Wel dus!)

Haai (1,1,3) kan (1,1,2) eten, en verder niet. (3,1,1) kan (2,1,1) eten. (3,3,3) eet alle drie de haaien uit het eerste rijtje.

Om vervolgens dit stukje te missen:

quote:

Op zondag 26 augustus 2007 12:32 schreef GlowMouse het volgende:

[..]
]
De volgorde wordt dan:
[(3,3,3), (1,1,3), (3,1,1), (1,1,2), (2,1,1), (1,2,1)]
(3,1,1) eet (2,1,1) op, (1,1,3) eet (1,1,2) op, en (3,3,3) eet (1,1,3) en (3,1,1) op.

Dat haaien probleem ben ik overigens tegengekomen bij een wedstrijdje in het bedenken en programmeren van algoritmes. Dergelijke wedstrijden worden vrijwel wekelijks door topcoder georganiseerd. Je krijgt dan 75 minuten de tijd om drie problemen van verschillende moeilijkheid op te lossen (de haaien waren lastig ). Als je dat heel goed doet, stijgt je rating en anders zakt ie natuurlijk. Voor degenen die zulk soort dingen leuk vinden, is het absoluut een aanrader!

Ik heb een probleem met een wiskunde project. Het gaat over grafen. De opgave is:
Hoeveel 2-reguliere grafen G=(V,E) bestaan er met V={1,2,3,4,5,6}? En hoeveel 3-reguliere grafen?
Onze hele klas (6VWO) komt er niet uit, en de leraar werkt niet mee. Wijzelf dachten 60, maar dat was in elk geval niet goed, er moet nog iets bij volgens de projectleidster.
Iemand die mij kan helpen?

quote:

Op donderdag 6 september 2007 16:23 schreef Leso_Varen het volgende:
Ik heb een probleem met een wiskunde project. Het gaat over grafen. De opgave is:
Hoeveel 2-reguliere grafen G=(V,E) bestaan er met V={1,2,3,4,5,6}? En hoeveel 3-reguliere grafen?
Onze hele klas (6VWO) komt er niet uit, en de leraar werkt niet mee. Wijzelf dachten 60, maar dat was in elk geval niet goed, er moet nog iets bij volgens de projectleidster.
Iemand die mij kan helpen?

Wat maakt een graaf verschillend? 2 reguliere grafen zijn per definitie alleen cykels (i.e. rondjes), dus op 6 punten heb je of:


Of:

De labelling maakt het dan eventueel verschillend. Voor een 3 reguliere graaf begin je met de cykel op zes punten:



Immers, twee losse grafen zijn niet mogelijk, daar je als je 1 punt 3 buren geeft, al 4 van de 6 punten gebruikt. De andere twee moeten bij je graaf.

Je krijgt dus:



Andere mogelijkheden zijn voor de basisstructuur niet. Aangezien zo'n graaf symmetrisch is maakt het in beginsel niet uit met welke knoop je begint. In de rechtse is elke knoop verbonden met de knoop 3 stapjes verder over de cykel. In de 2e is je beginknoop verbonden met twee stapjes over de cykel (duidelijk anders). Dat kun je met nog 1 knoop doen, 2 stapjes de andere kant op. Je kunt ze niet alle 3 2 stapjes over de cykel heen doen. Want dan krijg je dat er 1 knoop vier lijnen krijgt (2 stapjes de ene kant op verbonden, 2 stapjes de andere kant op met 1 knoop verbonden); ergo, je houdt deze twee over.

Dus ik zou zeggen, feitelijk zijn er slechts 2 verschillende grafen mogelijk bij 2 regulier, en 2 bij drie regulier.

Dan kun je je verder druk maken over de labelling (toewijzing welke knopen welk nummer krijgen):

Op de eerste graaf met 2 x 3 maakt de volgorde op de cykel niet uit. Je krijgt het aantal door (6 boven 3) te doen. Dat geeft 20 mogelijkheden. Als je er 3 voor 1 driehoek hebt gekozen, liggen de volgende 3 direct vast voor de andere driehoek.

Voor de cykel. In totaal zijn er 6! = 720 rijtjes mogelijk van zes getallen, maar aangezien het cyclisch is het rijtje 123456 op de graaf niet anders dan 612345, of 561234. Etc. Je telt dus 6x te veel rijtjes in feite. Dus: 720/6 = 120 die je nog overhoudt. En dan kun je nog gratis spiegelen. Dus dan houd je er nog maar 60 over. (Hier kan ik trouwens miszitten. Ik vertel me nog wel eens met zulk soort dingen).

Geeft 60 + 20 voor de 2-reguliere.

De drie reguliere is op zich ongeveer gelijk. Bij rechter van de 2 zijn alle knopen equivalent. Je hebt hier dus weer 60 rijtjes. Bij de rechter zijn de knopen niet per se equivalent. Daar moet ik even langer over nadenken, maar heb ik geen tijd voor.

[edit]

Er schoot me het volgende te binnen, je hebt feitelijk deze 3 labellingen:



Je ziet dat deze, ondanks dat ze alleen maar verschoven zijn langs de graaf via de cykel wel degelijk anders zijn. In de eerste zijn de buren van 1 : {2, 5, 6}, bij de 2e zijn de buren van 1: {2,3,6}, en bij de derde: {2,4,6}. Draai je verder, dan kom je weer op een situate uit die je al hebt, nl. dat 1 buur is van {2,5,6}. Dus, van alle rijtjes is de helft maar echt anders. Het rijtje 123456 verschilt niet van 456123 (d.w.z. als je linksboven begint te nummeren en met de klok meegaat en dan bekijkt welke buren elk punt heeft). En idem voor andere rijtjes. Van de 6! = 720 houd je er dus nog 360 over. Maar, dat is ook nog niet alles. Want, je ziet dat de rechter graaf spiegelsymmetrisch is. 654321 levert dezelfde graaf op, maar dan gespiegeld. Dat is niet 'echt' een andere graaf. Verder zie je dat dit voor de andere 2 ook geldt. Enfin, volgens mij kom je dan (misschien dat er nog wat mis hoor...) op 360 / 2 = 180 over.

Maar goed, dit is wel het idee... hopelijk heb je er wat aan.

[ Bericht 20% gewijzigd door Iblis op 06-09-2007 21:18:06 ]

een lineaire vectorruimte kan je zien als een additief geschreven abelse groep waarop een lichaam K werkt. Als ik kijk naar de defintie van zo'n vectorruimte dan kan ook een commutatieve ring nemen in plaats van een lichaam, nergens staat er iets over een inverse van een element uit K. Is dat zo? Leidt de werking van een commutatieve ring op een addetief geschreven abelse groep tot een lineaire vectorruimte?..wat gaat mis?

quote:

Op donderdag 6 september 2007 21:00 schreef Iblis het volgende:

[..]Uitleg.

Maar goed, dit is wel het idee... hopelijk heb je er wat aan.

Hartstikke bedankt Hier kom ik verder mee, echt top

quote:

Op donderdag 6 september 2007 21:23 schreef teletubbies het volgende:
een lineaire vectorruimte kan je zien als een additief geschreven abelse groep waarop een lichaam K werkt. Als ik kijk naar de defintie van zo'n vectorruimte dan kan ook een commutatieve ring nemen in plaats van een lichaam, nergens staat er iets over een inverse van een element uit K. Is dat zo? Leidt de werking van een commutatieve ring op een addetief geschreven abelse groep tot een lineaire vectorruimte?..wat gaat mis?

Volgens mij heb je gelijk. Je hebt een scalaire vermenigvuldiging nodig, maar deze hoeft niet inverteerbaar te zijn in een lineaire ruimte.

quote:

Op donderdag 6 september 2007 21:23 schreef teletubbies het volgende:
een lineaire vectorruimte kan je zien als een additief geschreven abelse groep waarop een lichaam K werkt. Als ik kijk naar de defintie van zo'n vectorruimte dan kan ook een commutatieve ring nemen in plaats van een lichaam, nergens staat er iets over een inverse van een element uit K. Is dat zo? Leidt de werking van een commutatieve ring op een addetief geschreven abelse groep tot een lineaire vectorruimte?..wat gaat mis?

In dat geval heet het geen vectorruimte, maar een moduul. Hierbij hoeven we niet eens aan te nemen dat de ring commutatief is.

Even een simpel vraagje: als G de groeifactor is per 3 dagen, is de groeifactor per uur dan gewoon G^1/72?

Correct.

quote:

Op vrijdag 7 september 2007 09:42 schreef thabit het volgende:

[..]

In dat geval heet het geen vectorruimte, maar een moduul. Hierbij hoeven we niet eens aan te nemen dat de ring commutatief is.

Okey,
een andere vraag, kansrekening/statistiek en algebra lijken me twee zaken die veel van elkaar verschillen, toch ben ik nieuwsgierig naar kansen in algebra, bijv bij groepen ofzo... ik zag ooit iets wat te maken met kansen bij groepen en het had te maken met een of andere soort deler/orde of iets dergelijks...
kun je me bijv nuttig links geven

quote:

Op zaterdag 8 september 2007 23:54 schreef teletubbies het volgende:

[..]

Okey,
een andere vraag, kansrekening/statistiek en algebra lijken me twee zaken die veel van elkaar verschillen, toch ben ik nieuwsgierig naar kansen in algebra, bijv bij groepen ofzo... ik zag ooit iets wat te maken met kansen bij groepen en het had te maken met een of andere soort deler/orde of iets dergelijks...
kun je me bijv nuttig links geven

Veel mensen die zich met algebra bezighouden interesseren zich niet voor statistiek en veel mensen die zich met statistiek bezighouden hebben geen zin om algebra te leren. Gevolg is dat er niet veel verbanden tussen de vakgebieden bekend zijn. Ik heb er zelf in elk geval vrij weinig van gezien.

Er bestaat wel zoiets als ergodentheorie voor topologische groepen. Random matrix theorie heeft hier en daar wat toepassingen in de L-functies. Bepaalde stukken statistische analyse op Riemannoppervlakken hebben weer raakvlakken met arithmetische meetkunde. Verder kun je wat kansrekening loslaten op de analyse van probabilistische algoritmen in de getaltheorie. En om bepaalde voortbrengen functies in de combinatoriek te bestuderen zul je ook vast stukken algebra toepassen.

Ook weer even een vraag:

quote:

Use taylor expansions to establish the order (as h -> 0) of:
f(x) = e^h-(1+h)

Eigenlijk snap ik de vraag al niet. Wat willen ze nu precies.

Om maar even een begin te maken:


De taylor polynoom is:
p(x) = u(0) + Du(0)/1! *x + D²u(0)/2! *x² + .. + Dⁿu(0)/n! *xⁿ

Waar Du de eerste afgeleide is D²u de tweede enz.

Df(x) = e^h - 1
D²f(x) = e^h
D³f(x) = e^h
und so weiter.

dus:

p(h) = 0 + 0/1 * h +1/2 *h² + 1/6 * h³ ...
= 1/2 *h² + 1/6 * h³ ...
= Sigma n=2 tot oneindig e^h/n! *hⁿ

En nu?

[edit] ik heb nu eigenlijk de helft van de h's wel en de andere helft niet ingevuld, geen idee waarom ik dat heb gedaan, snap er toch geen bal van.

[ Bericht 5% gewijzigd door Schuifpui op 10-09-2007 19:14:12 ]

quote:

Op maandag 10 september 2007 19:05 schreef Schuifpui het volgende:
Ook weer even een vraag:
[..]

Eigenlijk snap ik de vraag al niet. Wat willen ze nu precies.

Om maar even een begin te maken:


De taylor polynoom is:
p(x) = u(0) + Du(0)/1! *x + D²u(0)/2! *x² + .. + Dⁿu(0)/n! *xⁿ

Waar Du de eerste afgeleide is D²u de tweede enz.

Df(x) = e^h - 1
D²f(x) = e^h
D³f(x) = e^h
und so weiter.

dus:

p(h) = 0 + 0/1 * h +1/2 *h² + 1/6 * h³ ...
= 1/2 *h² + 1/6 * h³ ...
= Sigma n=2 tot oneindig e^h/n! *hⁿ

En nu?

[edit] ik heb nu eigenlijk de helft van de h's wel en de andere helft niet ingevuld, geen idee waarom ik dat heb gedaan, snap er toch geen bal van.

De 'orde' geeft aan met welk polynoom je functie 'vergelijkbaar' is in de omgeving van 0. Dwz zoek polynoom p zodat f(x)/p(x) convergeert voor x -> 0 naar een 'mooie' limiet, dwz geen 0 of oneindig. Jouw Taylorbenadering laat zien dat p tweedegraads moet zijn en dat f(x)/p(x) = 1/2 + <hogere orde termen> voor x -> 0, waarbij <hogere orde termen> staan voor de overige machten die naar 0 gaan als x -> 0. Dit wordt vaak genoteerd als "f(x) ~ (1/2)*x^2 voor x -> 0".

.

[ Bericht 7% gewijzigd door keesjeislief op 10-09-2007 19:27:35 ]

quote:

Op maandag 10 september 2007 19:21 schreef keesjeislief het volgende:

[..]

De 'orde' geeft aan met welk polynoom je functie 'vergelijkbaar' is in de omgeving van 0. Dwz zoek polynoom p zodat f(x)/p(x) convergeert voor x -> 0 naar een 'mooie' limiet, dwz geen 0 of oneindig. Jouw Taylorbenadering laat zien dat p tweedegraads moet zijn en dat f(x)/p(x) = 1/2 + <hogere orde termen> voor x -> 0, waarbij <hogere orde termen> staan voor de overige machten die naar 0 gaan als x -> 0. Dit wordt vaak genoteerd als "f(x) ~ (1/2)*x^2 voor x -> 0".

.

Thanks ik denk dat ik heel vaag een klein beetje begin te begrijpen. We werken ook met Landau symbolen en die f(x)/p(x) komt me dan wel bekend voor. Dus incl Landau kan ik zeggen dat f(x) = 1/2x² +O(x³)?

Moet het trouwens niet naar 2 zijn dan? (delen door een half)

Nog even een edit, want eigenlijk snap ik het toch niet.

f(x)/p(x) = [e^h-(1+h)]/[e^h/2*h² + ... ]

Voor h -> 0 wordt dit toch geen half (of twee) of zie ik het nou verkeerd?

[ Bericht 9% gewijzigd door Schuifpui op 10-09-2007 19:58:24 ]

quote:

Op maandag 10 september 2007 19:41 schreef Schuifpui het volgende:

[..]

Thanks ik denk dat ik heel vaag een klein beetje begin te begrijpen. We werken ook met Landau symbolen en die f(x)/p(x) komt me dan wel bekend voor. Dus incl Landau kan ik zeggen dat f(x) = 1/2x² +O(x³)?

Moet het trouwens niet naar 2 zijn dan? (delen door een half)

Ja, dat klopt. Om helemaal precies te zijn zou je eigenlijk nog "x -> 0" aan de uitdrukking moeten toevoegen. Het is niet zo moeilijk hoor, het gaat er gewoon om het limietgedrag van de functie uit te drukken in makkelijkere termen. Dit wordt meestal in termen van machtsfuncties gedaan, dwz x -> x^a, maar dat hoeft niet noodzakelijkerwijs, het kan ook een andere familie van functies x -> g_a(x) zijn.

Het nut van dit soort uitdrukkingen is dat je bijv. makkelijker de limiet van verschillende uitdrukkingen met elkaar kunt vergelijken als je eerst ieder van die uitdrukkingen in zulke makkelijkere termen schrijft. Nog een tip is dat je in een aantal gevallen makkelijke trucs hebt om ingewikkelde uitdrukkingen asymptotisch te ontwikkelen, zoals partiële integratie wanneer je met integralen van doen hebt.

quote:

Op maandag 10 september 2007 19:41 schreef Schuifpui het volgende:

[..]

Thanks ik denk dat ik heel vaag een klein beetje begin te begrijpen. We werken ook met Landau symbolen en die f(x)/p(x) komt me dan wel bekend voor. Dus incl Landau kan ik zeggen dat f(x) = 1/2x² +O(x³)?

Moet het trouwens niet naar 2 zijn dan? (delen door een half)

Nog even een edit, want eigenlijk snap ik het toch niet.

f(x)/p(x) = [e^h-(1+h)]/[e^h/2*h² + ... ]

Voor h -> 0 wordt dit toch geen half (of twee) of zie ik het nou verkeerd?

Sorry, mijn notatie was een beetje verwarrend. Je hebt gegeven de functie f(h) = e^h-(1+h). Met behulp van Taylor had jij al f(h) = (1/2)*h² + O(h³). Dit laat meteen zien dat f van orde 2 is dichtbij 0, nl. met p(h)=h² vind je f(h)/p(h) = 1/2 + O(h), dus f(h)/p(h) -> 1/2, wat betekent dat f en p "van dezelfde orde" zijn voor h -> 0. Duidelijk?

Ik denk dat ik het zo ga snappen, moet nu even weg, kijk er morgen even iets uitgebreider naar.

Heel veel dank iig.

Ik zie me weer genoodzaakt de hulp van Glowmouse/Riparius/KeesjeisLief ijn te roepen. Kan er iemand mij de afleiding van de "Euler chain relation"/"triple product rule" (hoe je het beestje noemen wilt) van a tot z uitleggen? Onthouden en toepassen is totaal geen probleem (δy/δx_z * δz/δy_x * δx/δz_y = -1), alleen de afleidingen die ik tot nu toe heb gevonden zijn zo counterintuitief als wat.

quote:

Op vrijdag 14 september 2007 14:55 schreef harrypiel het volgende:
Ik zie me weer genoodzaakt de hulp van Glowmouse/Riparius/KeesjeisLief ijn te roepen. Kan er iemand mij de afleiding van de "Euler chain relation"/"triple product rule" (hoe je het beestje noemen wilt) van a tot z uitleggen? Onthouden en toepassen is totaal geen probleem (δy/δx_z * δz/δy_x * δx/δz_y = -1), alleen de afleidingen die ik tot nu toe heb gevonden zijn zo counterintuitief als wat.

Kijk hier eens, echt veel duidelijker zou ik het zelf ook niet uit kunnen leggen. En anders moet je misschien eens in het Euler archief gaan zoeken om te kijken hoe Euler het zelf deed.

Hoi! geldt dat R en R^opp (tegengestelde ring) isomorf zijn dan en slechts dan als R commutatief is? mag ik een hint!
Thanks!

quote:

Op zaterdag 15 september 2007 19:53 schreef teletubbies het volgende:
Hoi! geldt dat R en R^opp (tegengestelde ring) isomorf zijn dan en slechts dan als R commutatief is? mag ik een hint!
Thanks!

hoii, het antwoord is nee, ik denk momenteel aan H (dat met quaternionen). Als ik niet een isomorfie vind,post ik hier weer een bericht..
Is er nog een voorbeeld ?

Even nog een iets simpelere:

If f^2 - g^2 = -10 and f + g = 2, than what is the value of f - g?

Het antwoord moet zijn -5

quote:

Op zaterdag 15 september 2007 20:42 schreef teletubbies het volgende:

[..]

hoii, het antwoord is nee, ik denk momenteel aan H (dat met quaternionen). Als ik niet een isomorfie vind,post ik hier weer een bericht..
Is er nog een voorbeeld ?

Met quaternionen gaat het niet lukken: stuur a + ib + jc + kd naar a - ib - jc - kd, dat is een isomorfisme van H naar H^opp.
Ik zit zelf meer te denken aan het volgende: neem Q[X,Y], maar dan met een vreemd soort vermenigvuldiging: YX=X²Y.

edit: O, hmm. Je bent op zoek naar een niet-commutatieve ring die isomorf is met z'n tegengestelde, niet naar een die er niet mee isomorf is. In dat geval werken de quaternionen dus wel. .

quote:

Op maandag 17 september 2007 13:55 schreef thabit het volgende:

[..]

Met quaternionen gaat het niet lukken: stuur a + ib + jc + kd naar a - ib - jc - kd, dat is een isomorfisme van H naar H^opp.
Ik zit zelf meer te denken aan het volgende: neem Q[X,Y], maar dan met een vreemd soort vermenigvuldiging: YX=X²Y.

edit: O, hmm. Je bent op zoek naar een niet-commutatieve ring die isomorf is met z'n tegengestelde, niet naar een die er niet mee isomorf is. In dat geval werken de quaternionen dus wel. .

okey dank je, maar ' stuur a + ib + jc + kd naar a - ib - jc - kd' is inderdaad handiger.

quote:

Op dinsdag 18 september 2007 18:04 schreef teletubbies het volgende:

[..]

okey dank je, maar ' stuur a + ib + jc + kd naar a - ib - jc - kd' is inderdaad handiger.

Die andere ring die ik noemde is juist niet isomorf met z'n tegengestelde.

Kan iemand me deze uitleggen, ik zie niet hoe "FE, ED equal to the square of the tangent E is" in de bewijsvoering.


Given a circle ABC and two points D, E external to it, to draw straight lines DB, EB from D, E to a point B on the circle such that, if DB, EB produced meet the circle again in C, A, AC shall be parallel to DE.

quote:

Op woensdag 19 september 2007 21:40 schreef Ogala het volgende:
Kan iemand me deze uitleggen, ik zie niet hoe "FE, ED equal to the square of the tangent E is" in de bewijsvoering.


Given a circle ABC and two points D, E external to it, to draw straight lines DB, EB from D, E to a point B on the circle such that, if DB, EB produced meet the circle again in C, A, AC shall be parallel to DE.

[afbeelding]

Wat is nu precies de vraag, kun je het wat duidelijker formuleren?

quote:

Op woensdag 19 september 2007 22:36 schreef keesjeislief het volgende:
[..]
Wat is nu precies de vraag, kun je het wat duidelijker formuleren?

(Part I. Construction.)

1. Suppose the circle ABC and the points D, E given.

2. Take a rectangle contained by ED and by a certain straight line EF equal to the square on the tangent to the circle from E.

3. From F draw FA touching the circle in A; join ABE and then DB, producing DB to meet the circle at C. Join AC.

I say then that AC is parallel to DE.

Ik snap puntje 2 dus niet bij het construeren (EF = square on the tangent to E) en zodoende in de bewijsvoering dus ook niet dat FE,ED = to the square of the tangent E.

quote:

Op woensdag 19 september 2007 22:54 schreef Ogala het volgende:

[..]

(Part I. Construction.)

1. Suppose the circle ABC and the points D, E given.

OK.

quote:

2. Take a rectangle contained by ED and by a certain straight line EF equal to the square on the tangent to the circle from E.

Hiermee wordt bedoeld dat je op het verlengde van ED een punt F moet bepalen, zodanig dat ED∙EF gelijk is aan het kwadraat van de lengte van de raaklijn aan de cirkel vanuit punt E. Deze raaklijn heb je niet getekend in je figuur.

De reden om punt F zo te bepalen is gelegen in een bekende stelling van Euclides (Boek III, stelling 36). Volgens deze stelling is namelijk het kwadraat van de lengte van de raaklijn aan de cirkel vanuit punt E gelijk aan het product EB∙EA. En aangezien het kwadraat van de lengte van de raaklijn aan de cirkel vanuit punt E ook gelijk is aan ED∙EF hebben we dus EB∙EA = ED∙EF.

quote:

3. From F draw FA touching the circle in A; join ABE and then DB, producing DB to meet the circle at C. Join AC.

I say then that AC is parallel to DE.

Ik snap puntje 2 dus niet bij het construeren (EF = square on the tangent to E) en zodoende in de bewijsvoering dus ook niet dat FE,ED = to the square of the tangent E.

If x is an integer and 2 < x < 7 , how many different triangles are there with sides of lengths 2, 7 and x?

Het antwoord moet zijn een. Waarom?

x mag dus 3, 4, 5 of 6 zijn.
x = 3 kan niet, want dan heb je een driehoek met zijde 2, 3, 7 en dan kan niet. (De 2 kleinste zijden moeten samen meer zijn dan de langste zijde)
x = 4 idem.
x = 5 wordt ook lastig Een driehoek met zijde van 2, 5 en 7 is niet haalbaar. Probeer maar eens te tekenen. Zie het als een graaf. Een omweg kan nooit korter of evenlang zijn als rechtstreeks.
x= 6 is de enige die kan.

quote:

Op donderdag 20 september 2007 09:31 schreef Riparius het volgende:
...Hiermee wordt bedoeld dat je op het verlengde van ED een punt F moet bepalen, zodanig dat ED∙EF gelijk is aan het kwadraat van de lengte van de raaklijn aan de cirkel vanuit punt E. Deze raaklijn heb je niet getekend in je figuur.

De reden om punt F zo te bepalen is gelegen in een bekende stelling van Euclides (Boek III, stelling 36).
...

Thnx die stelling had ik nog niet gezien (achteraf gezien heel logisch)

quote:

Op donderdag 20 september 2007 21:24 schreef Ogala het volgende:

[..]

Thnx die stelling had ik nog niet gezien (achteraf gezien heel logisch)

Ja. Alleen zijn we er hiermee nog niet. Zoals gezegd hebben we EB∙EA = ED∙EF, waaruit volgt dat de punten A,B,D,F op een cirkel liggen, of anders gezegd, ABDF is een koordenvierhoek (begrijp je dat ook?). Nu zijn de overstaande hoeken in een koordenvierhoek supplementair, en dus is hoek FAE gelijk aan hoek BDE. So far so good. Maar dan zegt Heath:

quote:

But the angle FAE is equal to the angle ACB in the alternate segment

En dat zie ik dus even niet. Ik begrijp met name niet wat Heath bedoelt met the alternate segment. Die term is niet gebruikelijk, en wordt verder in het hele betoog ook niet gebruikt, zodat niet duidelijk is waar hij op doelt. Nu jij weer ...

[ Bericht 1% gewijzigd door Riparius op 20-09-2007 22:47:48 ]

quote:

Op donderdag 20 september 2007 21:41 schreef Riparius het volgende:
... ABDF is een koordenvierhoek (begrijp je dat ook?). Nu zijn de overstaande hoeken in een koordenvierhoek supplementair, en dus is hoek FAE gelijk aan hoek BDE..

Yup concyclic quadrilateral, Book III Proposition 22

quote:

...wat Heath bedoelt met the alternate segment....

alternate segment theorem (Heath heeft het probleem uit Hankel from Pappus)
The angles between a tangent and a chord through the point of contact are equal respectively to the angles in the alternate segment.


(heb ik wel even aangenomen anders kan ik alles tot aan het bestaan van een punt toe bewijzen )

[ Bericht 7% gewijzigd door Ogala op 20-09-2007 23:34:35 ]

quote:

Op donderdag 20 september 2007 23:11 schreef Ogala het volgende:

[..]

Yup concyclic quadrilateral, Book III Proposition 22
[..]

alternate segment theorem (Heath heeft het probleem uit Hankel from Pappus)
The angles between a tangent and a chord through the point of contact are equal respectively to the angles in the alternate segment.

[afbeelding]

Ah, dank je wel. Dat is inderdaad stelling 32 uit boek III bij Euclides. Dan is het bewijs helemaal duidelijk. Maar waarom wilde je uitgerekend dit bewijs bij Heath nalopen? Ik ben zelf erg geïnteresseerd in de geschiedenis van de wiskunde, dus vandaar dat ik het vraag.

quote:

Op donderdag 20 september 2007 23:39 schreef Riparius het volgende:
[..]
Ah, dank je wel. Dat is inderdaad stelling 32 uit boek III bij Euclides. Dan is het bewijs helemaal duidelijk. Maar waarom wilde je uitgerekend dit bewijs bij Heath nalopen? Ik ben zelf erg geïnteresseerd in de geschiedenis van de wiskunde, dus vandaar dat ik het vraag.

Ik ben pas begonnen met Book I en in de intro stond deze stelling als ideaal voorbeeld voor de analyse van problemen. (transformatie, resolutie, synthese) vandaar! Toch wel leuk om eens door te lezen!

Als I en J idealen zijn van een commutatieve ring R dan geldt (I +J)(I^J) C IJ. het symbool ^ staat voor de 'doorsende'. Is het waar dat voor iedere een commutatieve ring de gelijkheid t (I +J)(I^J) =IJ geldt? (zonder bewijs aub!)

quote:

Op zondag 23 september 2007 15:41 schreef teletubbies het volgende:
Als I en J idealen zijn van een commutatieve ring R dan geldt (I +J)(I^J) C IJ. het symbool ^ staat voor de 'doorsende'. Is het waar dat voor iedere een commutatieve ring de gelijkheid t (I +J)(I^J) =IJ geldt? (zonder bewijs aub!)

Nee.

quote:

Op zondag 23 september 2007 17:13 schreef thabit het volgende:

[..]

Nee.

nu begin ik een zochttocht naar een tegenvoorbeeld..
tot nu toe is me voorbeelden set bijna op!

Wat voor ringen heb je allemaal al uitgeprobeerd?

De ringen :d zijn Z[x], euuh R, C en Z.
Ik dacht aan endomorfismenring. Misschien ook groepenringen, matrices..
:S welke richting moet ik eigenlijk gaan?

Nog een vraagje, als I+J=R met I en J idealen die onderling ondeelbaar zijn en R is een ring. Ik moet laten zien dat
I^m+Jⁿ=R. Hiervoor heb ik inductie gebruikt, eerst heb ik laten zien dat:
I+Jⁿ=R voor n=1,2,3,...
Maar daarna wil ik n vast nemen en dan inductie gebruiken naar de macht van I. Ik heb al:
I²+Jⁿ=R maar verder kom ik niet uit..

ALvast bedankt

quote:

Op maandag 24 september 2007 13:16 schreef teletubbies het volgende:
De ringen :d zijn Z[x], euuh R, C en Z.
Ik dacht aan endomorfismenring. Misschien ook groepenringen, matrices..

In Z[x] moet het lukken een tegenvoorbeeld te vinden. Endomorfismen-, groepen- en matrixringen zijn iha niet commutatief.

quote:

Op maandag 24 september 2007 13:16 schreef teletubbies het volgende:
Nog een vraagje, als I+J=R met I en J idealen die onderling ondeelbaar zijn en R is een ring. Ik moet laten zien dat
I^m+Jⁿ=R. Hiervoor heb ik inductie gebruikt, eerst heb ik laten zien dat:
I+Jⁿ=R voor n=1,2,3,...
Maar daarna wil ik n vast nemen en dan inductie gebruiken naar de macht van I. Ik heb al:
I²+Jⁿ=R maar verder kom ik niet uit..

ALvast bedankt

Kun je dan niet je argument van 'eerst' toepassen op het paar (Jⁿ,I)? Die zijn immers ook onderling ondeelbaar.

OMG. Schaam me echt dood dat ik dit moet vragen, maar ben het echt eventjes helemaal kwijt. De resultant force van deze 2 forces is duidelijk. Gewoon een parallelogram van maken en dan weet je de resultant.



Maar wat als de forces er zo uitzien?

quote:

Op maandag 24 september 2007 22:12 schreef MaximumRush het volgende:
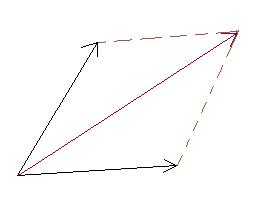
OMG. Schaam me echt dood dat ik dit moet vragen, maar ben het echt eventjes helemaal kwijt. De resultant force van deze 2 forces is duidelijk. Gewoon een parallelogram van maken en dan weet je de resultant.

[afbeelding]

Maar wat als de forces er zo uitzien?

[afbeelding,link]

Gewoon optellen kjal .

Vraagje over statistiek:

quote:

1. Stel de cumulatieve frequentieverdeling op.
2. Bepaal de cumulatieve frequentie die met het K-de percentiel correspondeert: nK/100
3. Zoek in de cumulatieve frequentieverdeling de klasse op waarin K-de percentiel moet liggen.
Dit is de klasse waarvan de cumulatieve frequentie net groter is dan (of gelijk is aan) nK/100. Van deze klasse bepalen we:
a) De frequentie f
b) De exacte benedengrens ll
c) De klassenbreedte w = verschil tussen de exacte boven- en benedengrens :

frequentie distributie:


Reken percentiel P10, P45, P60 en P90 uit
Formule


Wie kan me nu helpen met het invullen van de formule?

quote:

Op dinsdag 25 september 2007 19:55 schreef crossover het volgende:
Vraagje over statistiek:
[..]

frequentie distributie:

[ code verwijderd ]


Reken percentiel P10, P45, P60 en P90 uit
Formule
[afbeelding]

Wie kan me nu helpen met het invullen van de formule?

Ehm...
correct me if i'm wrong.
Je moet de formule invullen voor achtereenvolgens K = {10,45,60,90}
Als K=10 zoek je de bijbehorende entry in je tabel, dit is waar cF voor het eerst >= 10 (hier cF=14)
ll is dan 1.4 (exacte benedengrens iig)
w is 0.2 (boven - benedengrens)
cf is 14
f is 10

invullen, doorrekenen en klaar is klara, zelfde trucje herhalen voor K = 45, K=60 en K=90

En dat voor iemand die nooit statistiek gehad heeft

quote:

Op dinsdag 25 september 2007 20:03 schreef MPG het volgende:

[..]

Ehm...
correct me if i'm wrong.
Je moet de formule invullen voor achtereenvolgens K = {10,45,60,90}
Als K=10 zoek je de bijbehorende entry in je tabel, dit is waar cF voor het eerst >= 10 (hier cF=14)
ll is dan 1.4 (exacte benedengrens iig) 1.35
w is 0.2 (boven - benedengrens)
cf is 14 4
f is 10

invullen, doorrekenen en klaar is klara, zelfde trucje herhalen voor K = 45, K=60 en K=90

En dat voor iemand die nooit statistiek gehad heeft

Ben vergeten te vermelden dat cF betrekking heeft op de net lagere klasse. lower limit is 1.35.

N(totale scores) = 120?
Dat wordt dan 1.35+(120x10/100-4)/10 * 0.2 = 0.43

Edit: misschien klopt het niet dat cF correspondeert met de net lagere klasse, dan zou het 14 zijn en komt er 1.15 uit.

quote:

Op dinsdag 25 september 2007 20:13 schreef crossover het volgende:

[..]

Ben vergeten te vermelden dat cF betrekking heeft op de net lagere klasse. lower limit is 1.35.
[afbeelding]
N(totale scores) = 120?
Dat wordt dan 1.35+(120x10/100-4)/10 * 0.2 = 0.43

Edit: misschien klopt het niet dat cF correspondeert met de net lagere klasse, dan zou het 14 zijn en komt er 1.15 uit.

cF correspondeert voor zover ik uit hetgeen ik heb gelezen in jouw eerste post niet met de net lagere klasse. Jouw edit lijkt mij dan ook juist

Lieve mensen,

Ik was eens aan mijn achterstallig huiswerk begonnen en stuitte op dit prachtige iets.

e^-X+wortelY=1 In mijn boek zeggen ze ineens simpel dat je dit ook kunt schrijven als y = x^2, maar ik heb geen flauw idee hoe ze hierbij komen.

e^-x + SQRT(y) = 1
e^-x -1= SQRT(y)
kwadateren levert e^-2x -2e^-x + 1 = y (merkwaardig product)
stel e^-x = p ; daaruit volgt p² - 2p + 1 = y

nu moet het moet niet zo moeilijk zijn om nulpunten te bereken.

[ Bericht 0% gewijzigd door harrypiel op 26-09-2007 15:08:51 ]

quote:

Op woensdag 26 september 2007 13:07 schreef moeffiemoeffie het volgende:
Lieve mensen,

Ik was eens aan mijn achterstallig huiswerk begonnen en stuitte op dit prachtige iets.

e^-X+wortelY=1 In mijn boek zeggen ze ineens simpel dat je dit ook kunt schrijven als y = x^2, maar ik heb geen flauw idee hoe ze hierbij komen.

e^-x+wortel(y) = 1

e^x = a is hetzelfde als x = ln(a)

dus -x+wortel(y) = ln(1)
ln(1) = 0
dus -x+wortel(y) = 0
dus wortel(y) = x
dus y = x²

Zorg er wel voor dat je goed met haakjes werkt als je een macht aangeeft met ^, anders krijg je dus antwoorden als die van meneer piel te zien.

[ Bericht 29% gewijzigd door Jordy-B op 26-09-2007 13:24:07 ]

quote:

Op woensdag 26 september 2007 13:17 schreef Jordy-B het volgende:

[..]

e^-x+wortel(y) = 1

e^x = a is hetzelfde als x = ln(a)

dus -x+wortel(y) = ln(1)
ln(1) = 0
dus -x+wortel(y) = 0
dus wortel(y) = x
dus y = x²

Zorg er wel voor dat je goed met haakjes werkt als je een macht aangeeft met ^, anders krijg je dus antwoorden als die van meneer piel te zien.

anders met _{tekst in subscript} of ^{tekst in superscript} werken om de zaak te verduidelijken

_{druk op de quote bericht knop voor de precieze code}