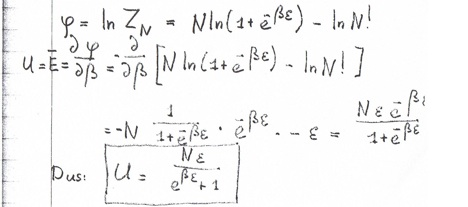SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Je stelt V en 4 samen. Je bent dan in wezen 2 factoren boven de x-as. Neem je de verticale componenten van 2 en 3 dan kom je op de x-as. (x-as is dus lijn AB)quote:Op zaterdag 14 juli 2007 00:57 schreef GlowMouse het volgende:
Wanneer je V en 4 samentstelt, en daarna nog eens 2, 3 en 4 erachteraan plakt, kom je toch niet op lijn AB uit?
De horizontale component maakt in principe niet meer uit.
Vroeger dacht ik dat ik mijn vijanden het vuur aan de schenen moest leggen. Een misvatting, want dat doen ze zelf wel. Ik hoef enkel mijn vergrootglas maar op ze te richten en het begint te smeulen.


Ja, waarom dan toch antwoord D? V+2+3+4 ligt op AB. Dus als je V en 2 hebt, heb je als overige vectoren alleen nog maar 3+4 nodig.
Je hebt dus of de vraag verkeerd gesteld of je moet de vraag nog eens doorlezen. We bedoelen in ieder geval hetzelfde.
Je hebt dus of de vraag verkeerd gesteld of je moet de vraag nog eens doorlezen. We bedoelen in ieder geval hetzelfde.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Waarschijnlijk het eerste. Ik was teveel gericht op de horizontale component tewijl die niks uitmaakt.quote:Op zaterdag 14 juli 2007 01:39 schreef GlowMouse het volgende:
Ja, waarom dan toch antwoord D? V+2+3+4 ligt op AB. Dus als je V en 2 hebt, heb je als overige vectoren alleen nog maar 3+4 nodig.
Je hebt dus of de vraag verkeerd gesteld of je moet de vraag nog eens doorlezen. We bedoelen in ieder geval hetzelfde.
Vroeger dacht ik dat ik mijn vijanden het vuur aan de schenen moest leggen. Een misvatting, want dat doen ze zelf wel. Ik hoef enkel mijn vergrootglas maar op ze te richten en het begint te smeulen.


Hey, dit is een opgave waarbij ik het gevoel heb dat ik teveel doordenk en moeilijk doe. De opgave lijkt erg vanzelfsprekend.
Stel G en G' zijn twee isomorfe groepen. Ik moet bewijzen dat de orde van Aut(G) is gelijk aan het aantal isomorfismen van G naar G'.
Ik denk het volgende:
Ik weet dat er in ieder geval een isomorfisme bestaat tussen G en G'. Noem deze I. Zij A een automorfisme van G.
Bekijk de afbeelding f van permutaties1 van G naar permutaties2 van G'(....ik weet niet hoe ik deze precies moet definieren: met permutaties1: bedoel ik permutaties veroorzaakt alleen door automorfismen van G. Met permutaties2: bedoel ik alleen permutaties als gevolg van isomorfismen G-->G.
Nogmaals ik doe denk ik moeilijk..)
f: I*A(G).
Deze stuurt een permutatie van G (veroorzaakt door A) naar een permutatie van G' (veroorzaakt door I*A(G)). Dit is een bijectieve afbeelding, want I en A zijn bijecties en de samenstelling ervan dus ook. Als we A laten lopen over de elementen van Aut(G) dan krijgen we steeds een andere f.
Nu wil ik aantonen dat f ook surjectief is, heb je misschien een hint? want dan heb ik een bijectie en ben ik klaar.
Heb je een idee hoe deze opgave eleganter opgelost kan worden?
Alvast bedankt..
Stel G en G' zijn twee isomorfe groepen. Ik moet bewijzen dat de orde van Aut(G) is gelijk aan het aantal isomorfismen van G naar G'.
Ik denk het volgende:
Ik weet dat er in ieder geval een isomorfisme bestaat tussen G en G'. Noem deze I. Zij A een automorfisme van G.
Bekijk de afbeelding f van permutaties1 van G naar permutaties2 van G'(....ik weet niet hoe ik deze precies moet definieren: met permutaties1: bedoel ik permutaties veroorzaakt alleen door automorfismen van G. Met permutaties2: bedoel ik alleen permutaties als gevolg van isomorfismen G-->G.
Nogmaals ik doe denk ik moeilijk..)
f: I*A(G).
Deze stuurt een permutatie van G (veroorzaakt door A) naar een permutatie van G' (veroorzaakt door I*A(G)). Dit is een bijectieve afbeelding, want I en A zijn bijecties en de samenstelling ervan dus ook. Als we A laten lopen over de elementen van Aut(G) dan krijgen we steeds een andere f.
Nu wil ik aantonen dat f ook surjectief is, heb je misschien een hint? want dan heb ik een bijectie en ben ik klaar.
Heb je een idee hoe deze opgave eleganter opgelost kan worden?
Alvast bedankt..
verlegen :)


Je doet wel een beetje moeilijk. Je hoeft het niet zo in termen van permutaties te formuleren. Gewoon aantonen dat de afbeelding Aut(G) -> Aut(G') gedefinieerd door sigma -> I*sigma*I-1 een isomorfisme is (hint: ga na dat tau -> I-1*tau*I een inverse is).


Okey.. dit lijkt min of meer een op een conjugatiebewerking.quote:Op maandag 23 juli 2007 23:34 schreef thabit het volgende:
Je doet wel een beetje moeilijk. Je hoeft het niet zo in termen van permutaties te formuleren. Gewoon aantonen dat de afbeelding Aut(G) -> Aut(G') gedefinieerd door sigma -> I*sigma*I-1 een isomorfisme is (hint: ga na dat tau -> I-1*tau*I een inverse is).
De inversie is dan een kwestie van subsitueren, dat de kern alleen t eenheidselement bevat, is ook niet moeilijk en daaruit volgt dat de afbeelding injectief is.
Maar hoe weet ik of t bereik hele Aut(G') is?
dank je!
verlegen :)


Ik denk dat de truc waarnaar jij op zoek het zng. "kwadraat afsplitsen" is. Wat je in fiete probeert is een algemene ax^2 + bx + c te herschijven tot a(x + b)^2 + c . Het handigste is daarbij in eerste instantie te kijken welke a en b je nodig hebt. Van de merkwaardige producten weten we dat (x+p)^2 = x^2 + 2xp +p^2 oplevert. in het geval van y^2 - 2y + 2 hebben we a=1, b=-2 en c=2 (coefficienten abc-formule). We beginnen met de a-waarde en we moeten oplossen a=1; hieruit volgt dat 2yp = 2*1*p = -2, wat p = -1 oplevert. Gewapend daarmee kunnen we het kwadraat opstellen; (y-1)^2 + c = y^2 - 2y + 2. Schrijven we vervolgens het linkerlid uit dan komen we op y^2 - 2y + 1 uit, dus moeten we daar nog 1 bij optellen. We krijgen danquote:Op donderdag 5 juli 2007 15:31 schreef H4ze het volgende:
Ik ben een beetje bezig met de inverse van functies te berekenen en opzich lukt dat wel aardig. Echter heb ik nu een 2e graads functie voor me waarbij het me niet lukt....Dit heb ik zelf geprobeerd:
y = x^2 - 2x + 2
x = y^2 - 2y + 2
x-2 = y^2 -2y
wortel(x-2) = y-2y
wortel(x-2) = y(1-2) nu beide kanten door (1-2), oftewel -1 delen
wortel(x-2)/-1 = y
Dus bij mij is het antwoord y_inverse = wortel(x-2)/-1
Maar dit klopt uiteraard niet (ik heb zelf wat getallen bij beide ingevuld en zo). Volgens Maple is het correcte antwoord 1+wortel(x-1)...
Waar oh waar maak ik een domme fout?
(y-1)^2 + 1 = y^2 - 2y + 2 = x
(y-1)^2 + 1 = x
(y-1)^2 = x-1
y-1 = +/- SQRT(x-1)
y = 1 +/- SQRT(x-1)
Je had hem overigens bijna goed hoor; je vergat alleen het feit dat de wortel van een positieve uitdrukking zowel een positieve als een negatieve waarde kan hebben.
Edit: fouten verwijderd en wortels toegevoegd. Wil degene die mij gequote deze wijzigingen ook doorvoeren, anderd wordt het zo een zootje? BVD .
[ Bericht 5% gewijzigd door harrypiel op 31-07-2007 16:49:28 ]


Dat weet je dus doordat de afbeelding een inverse heeft.quote:Op donderdag 26 juli 2007 23:05 schreef teletubbies het volgende:
[..]
Maar hoe weet ik of t bereik hele Aut(G') is?


Is dit niet een beetje een omweg? Je kan toch gewoon, net als Glowmouse al hintte, de abc-formule gebruiken?quote:Op dinsdag 31 juli 2007 13:44 schreef harrypiel het volgende:
[..]
Ik denk dat de truc waarnaar jij op zoek het zng. "kwadraat afsplitsen" is. Wat je in fiete probeert is een algemene ax^2 + bx + c te herschijven tot a(x + b)^2 + c . Het handigste is daarbij in eerste instantie te kijken welke a en b je nodig hebt. Van de merkwaardige producten weten we dat (x+p)^2 = x^2 + 2xp +p^2 oplevert. in het geval van y^2 - 2y + 2 hebben we a=1, b=-2 en c=2 (coefficienten abc-formule). We beginnen met de a-waarde en we moeten oplossen a=1; hieruit volgt dat 2yp = 2*1*p = -2, wat p = -1 oplevert. Gewapend daarmee kunnen we het kwadraat opstellen; (y-1)^2 + c = y^2 - 2y + 2. Schrijven we vervolgens het linkerlid uit dan komen we (hoe toevallig) precies op y^2 - 2y + 2 uit, dus hoeven we niets bij ons kwadraat op te tellen of vanaf te trekken. Dus hebben we x = (y-1)^2 => +/- x = y-1 => 1+/- x = y.
Als y = x2 - 2x + 2,
Dan: x2 - 2x + (2-y) = 0
En dus:
x = (2 +/- sqrt(4 - 4(2-y)))/2 <-- Invullen abc-formule
Vereenvoudigen levert: x = 1 +/- sqrt(y-1)
Theories come and theories go. The frog remains


Het (meest gangbare) bewijs van de abc-formule leunt op het afsplitsen van het kwadraat, dus in feite doe je precies hetzelfde. Het voordeel van de manier van harrypiel is dat je wat beter weet waar je mee bezig bent.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Bovendien: als je functies in vorm van
ax^2 + bx + c
-------------------
dx^2 + ex + f
moet gaan integreren en komt na vereenvoudigen (staartdelingen!! yay, wat ben ik blij dat ik dat nog op de basisschool gehad heb), op iets als 1 / (ax^2 + bx +c) uitkomt, waarbij je in de noemer geen nulpunten kan vinden, dan kan je niet meer terugvallen op de abc-formule en moet je "kwadraat afsplitsen" toepassen. Dan kom je op uitdrukkingen als a*1 / (x + b)^2 + c uit, waar je dan vervolgens de juiste arctangens-functie bij moet vinden. nauwkeurig herleiden is een 1ste vereiste hierbij.
ax^2 + bx + c
-------------------
dx^2 + ex + f
moet gaan integreren en komt na vereenvoudigen (staartdelingen!! yay, wat ben ik blij dat ik dat nog op de basisschool gehad heb), op iets als 1 / (ax^2 + bx +c) uitkomt, waarbij je in de noemer geen nulpunten kan vinden, dan kan je niet meer terugvallen op de abc-formule en moet je "kwadraat afsplitsen" toepassen. Dan kom je op uitdrukkingen als a*1 / (x + b)^2 + c uit, waar je dan vervolgens de juiste arctangens-functie bij moet vinden. nauwkeurig herleiden is een 1ste vereiste hierbij.


Als zowel a als d ongelijk aan 0 zijn in je functie, lijkt het me sterk dat je iets krijgt in de vorm van 1/(ax²+bx+c).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ja, het is alleen de vraag of iemand als H4ze die kennelijk in de veronderstelling verkeerde dat de wortel uit y2 - 2y gelijk is aan y - 2y (sic) een kwadraatafsplitsing wel tot een goed einde weet te brengen ...quote:Op dinsdag 31 juli 2007 15:14 schreef GlowMouse het volgende:
Het (meest gangbare) bewijs van de abc-formule leunt op het afsplitsen van het kwadraat, dus in feite doe je precies hetzelfde. Het voordeel van de manier van harrypiel is dat je wat beter weet waar je mee bezig bent.


Nee, dat is ook niet zo. Delen levert dan een constante op plus een restbreuk waarbij de teller een eerstegraadsfunctie is in x. Door kwadraatafsplitsing toe te passen in de noemer (zonder reële nulpunten) en de teller te herschrijven kun je die restbreuk verder herleiden tot een som van twee breuken die wel te integreren zijn.quote:Op dinsdag 31 juli 2007 17:23 schreef GlowMouse het volgende:
Als zowel a als d ongelijk aan 0 zijn in je functie, lijkt het me sterk dat je iets krijgt in de vorm van 1/(ax²+bx+c).


het was ook om aan te geven dat je in bepaalde gevallen je aan "kwadraat afsplitsen" vast zit om bijv. een integratie tot een goed einde te brengen. Tuurlijk, als we de andere gevallen nalopen: is de noemer een:quote:Op dinsdag 31 juli 2007 17:23 schreef GlowMouse het volgende:
Als zowel a als d ongelijk aan 0 zijn in je functie, lijkt het me sterk dat je iets krijgt in de vorm van 1/(ax²+bx+c).
kwadratische functie - zonder nulpunten in R? primitieve bevat een arctangens (en hier moet je dan "kwadraat afsplitsen" toepassen) + eventueel een ln en een lineaire term
kwadratische functie - dubbel nulpunt in R? primitieve bevat een ln term + eventueel een lineaire term
kwadratische functie - twee nulpunten in R? primitieve bevat 2 ln termen (dat wordt breuksplitsen) + eventueel een lineaire term


Een vraagje over Hom(D3, A4). De vraag is, bepaal het aantal homomorfismen in deze groep.quote:Op dinsdag 31 juli 2007 13:47 schreef thabit het volgende:
[..]
Dat weet je dus doordat de afbeelding een inverse heeft.
A4 heeft geen ondergroep van orde 6. Waarom moet gelden dat het beeld van ieder homomorfisme van D3 naar A4 abels is?Wat is het verband ...?
Alvast bedankt
verlegen :)


Kom even niet uit een afleiding. Gaat met name om de laatste stap. Het diffrentieren volg ik alleen de conclusie U = .... kan ik even niet thuisbrengen. Kan iemand even de tussenstappen uitleggen?


Vermenigvuldig boven en onder met exp(beta*epsilon).
Alle eendjes zwemmen in het water. :)
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...


Wow, statistische mechanica . Energie van een fermiongas if i'm not mistaken. Anywayz hier de uitleg van de gebruikte wiskunde inde laatste stap.
e-x * ex = e-x+x = e0 = 1
e-x * ex = e-x+x = e0 = 1


Is dat streepje boven de E op de tweede regel trouwens een min-teken voor de dau-phi/dau-beta erna, of sluipt er ergens een minteken in?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Denk dat dat het symbool voor het gemiddelde is, in dit geval de gemiddelde energie.quote:Op vrijdag 17 augustus 2007 15:19 schreef GlowMouse het volgende:
Is dat streepje boven de E op de tweede regel trouwens een min-teken voor de dau-phi/dau-beta erna, of sluipt er ergens een minteken in?


Waar komt de min voor de N op de regel erna dan vandaan?quote:Op vrijdag 17 augustus 2007 15:20 schreef harrypiel het volgende:
[..]
Denk dat dat het symbool voor het gemiddelde is, in dit geval de gemiddelde energie.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Daar komt alleen de -epsilon term uit voort.quote:Op vrijdag 17 augustus 2007 15:27 schreef harrypiel het volgende:
Die komt dan weer van het differentieren van iets als ln(1+e-x) mbv de kettingregel.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


mss negatieve potentiele energie, net zoals je bij de grondtoestand van het H-atoom een waarde van -13,6 eV hebt en de geioniseerde toestand een potentiele energie van 0 heeft (geen binding met proton c.q. H-kern) ?


GlowMouse heeft gelijk, er zit daar op z'n minst een schrijffout.
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


"U en E-gemiddeld wordt gedefinieerd door - dφ/dβ, dus daar komt dat minteken voor de N vandaan." en de differentiatie is ook correct uitgevoerd. Yups, dat moet de juiste formule zijn


Ik snap het niet helemaal, de lengte en breedte kan je toch zo klein maken als je zelf wilt?
Edit: oh, je bedoelt het gehele oppervlak van de balk natuurlijk.
Inhoud is x*y*z. x=y en inhoud = 500cm², dus je kan zeggen x² * z = 500.
Gehele buitenoppervlak is 2x² + 4xz. Met z = 500 / x². Dus oppervlakte = 2x² + 4x*(500/x²) = 2x² + 2000x / x² = 2x² + 2000/x.
Ik doe dit even snel uit mijn hoofd, dus kan zijn dat ik er een klein beetje naast zit, maar anders moet je gewoon even een tekeningetje maken en de zijdes x, y en z noemen. Schrijf de oppervlakte van elk vlak als term van x, y en/of z en tel alle oppervlaktes bij elkaar op. Daarna toepassen dat je weet dat x=y en z = 500/x² en y en z substitueren door die uitdrukkingen.
[ Bericht 39% gewijzigd door Merkie op 19-08-2007 22:05:14 ]
Edit: oh, je bedoelt het gehele oppervlak van de balk natuurlijk.
Inhoud is x*y*z. x=y en inhoud = 500cm², dus je kan zeggen x² * z = 500.
Gehele buitenoppervlak is 2x² + 4xz. Met z = 500 / x². Dus oppervlakte = 2x² + 4x*(500/x²) = 2x² + 2000x / x² = 2x² + 2000/x.
Ik doe dit even snel uit mijn hoofd, dus kan zijn dat ik er een klein beetje naast zit, maar anders moet je gewoon even een tekeningetje maken en de zijdes x, y en z noemen. Schrijf de oppervlakte van elk vlak als term van x, y en/of z en tel alle oppervlaktes bij elkaar op. Daarna toepassen dat je weet dat x=y en z = 500/x² en y en z substitueren door die uitdrukkingen.
[ Bericht 39% gewijzigd door Merkie op 19-08-2007 22:05:14 ]
2000 light years from home


Inhoud ciilinder = pi*r²*z = 500. z = 500/(pi*r²)
Totale oppervlakte van een cilinder = 2pi*r² + z*2pi*r. Dit omdat je 2x een cirkel met oppervlakte pi*r² hebt, en een hoogte z * de omtrek van de cirkel (= 2pi * r).
Substitueren levert op: 2pi*r² + (2pi*r*500)/(pi*r²) = 2pi*r² + 1000 / r. Volgens mij.
Totale oppervlakte van een cilinder = 2pi*r² + z*2pi*r. Dit omdat je 2x een cirkel met oppervlakte pi*r² hebt, en een hoogte z * de omtrek van de cirkel (= 2pi * r).
Substitueren levert op: 2pi*r² + (2pi*r*500)/(pi*r²) = 2pi*r² + 1000 / r. Volgens mij.
2000 light years from home


Ja, mcrapts apending hotmail punt com.
[ Bericht 90% gewijzigd door Merkie op 19-08-2007 22:34:23 ]
[ Bericht 90% gewijzigd door Merkie op 19-08-2007 22:34:23 ]
2000 light years from home


Ik zie zo geen rekenfout hoor.quote:Op zondag 19 augustus 2007 22:21 schreef Merkie het volgende:
Inhoud ciilinder = pi*r²*z = 500. z = 500/(pi*r²)
Totale oppervlakte van een cilinder = 2pi*r² + z*2pi*r. Dit omdat je 2x een cirkel met oppervlakte pi*r² hebt, en een hoogte z * de omtrek van de cirkel (= 2pi * r).
Substitueren levert op: 2pi*r² + (2pi*r*500)/(pi*r²) = 2pi*r² + 1000 / r. Volgens mij.
Hee, net stond er in GJ's bericht nog dat je een fout had gemaakt
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Het enige niet-abelse quotient van D3 is D3 zelf (groepen van orde kleiner dan 6 zijn immers altijd abels). Als het beeld niet abels zou zijn, dan is het beeld dus isomorf met D3. Maar D3 heeft orde 6 en A4 heeft geen ondergroepen van orde 6.quote:Op maandag 6 augustus 2007 17:54 schreef teletubbies het volgende:
[..]
Een vraagje over Hom(D3, A4). De vraag is, bepaal het aantal homomorfismen in deze groep.
A4 heeft geen ondergroep van orde 6. Waarom moet gelden dat het beeld van ieder homomorfisme van D3 naar A4 abels is?Wat is het verband ...?
Alvast bedankt


Ik kijk nog eens naar dit vraagstuk, en ik heb hem opgelostquote:Op maandag 11 juni 2007 12:26 schreef Schuifpui het volgende:
Nieuwe dag, nieuwe kansen.
Dit keer van het estimation deel.
By means of the Global Positioning System (GPS) the six
height differences hi, i = 1, . . . , 6, as shown in Fig. 2 are
observed. The heights of points 1, 2 and 3 are assumed
known, the heights of points 4 and 5 are unknown. The
observables are hi = hi + ei, whereby it may be assumed
that E(ei) = 0 and D(ei) = 2 cm2 for i = 1, . . . , 6, and
C(ei, ej) = 0 for i 6= j. The variance of the BLUE of h1
is then given as
a) 8/11 cm2
b) 0 cm2
c) 6/11 cm2
d) 2 cm2
Geef de hoogte van de punten 1..5 aan met ai en de geobserveerde waarden voor h1...h6 met Hi. Dan heb ik zo vijf zuivere schatters voor h1:
h1 = E(H1)
h1 = E(a2 - H2 - a1)
h1 = E(a3 - H3 - a1)
h1 = E(a2 - H4 - H6 - a1)
h1 = E(a3 - H5 - H6 - a1)
Ik kan dus ook schrijven:
h1 = c1*E(H1) + c2*E(a2 - H2 - a1) + c3*E(a3 - H3 - a1) + c4*E(a2 - H4 - H6 - a1) + c5*E(a3 - H5 - H6 - a1)
Met c1+c2+c3+c4+c5 = 1.
De uitdrukking voor de variantie voor het rechterlid is 2(c1²+c2²+c3²+c4²+c5²) + 2(c4+c5)²
Nu kan ik de variantie minimaliseren over c1..c5, wat ik ook gedaan heb, en waar een variantie van 6/11 uitkomt. Ter volledigheid de gevonden waarden voor c:
c1 0,2727272727
c2 0,2727272727
c3 0,2727272727
c4 0,09090909091
c5 0,09090909091
Nu is het nog de vraag hoe dit kan zonder computer die een kwadratische functie minimaliseert.
[ Bericht 6% gewijzigd door GlowMouse op 21-08-2007 23:12:32 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0