Iemand die dit idee omver kan werpen?

quote:

---

Op dinsdag 2 september 2003 12:20 schreef smash789 het volgende:
Stel je hebt een ENORM grote schijf in de ruimte. Deze laat je vanuit het middelpunt draaien. Uiteindelijk moet het dan toch mogelijk zijn om sneller dan het licht te gaan? Hoe groter de schijf, hoe hoger de snelheid van de buitenste rand.

Iemand die dit idee omver kan werpen?

---

quote:

---

Op dinsdag 2 september 2003 12:20 schreef smash789 het volgende:
Stel je hebt een ENORM grote schijf in de ruimte. Deze laat je vanuit het middelpunt draaien. Uiteindelijk moet het dan toch mogelijk zijn om sneller dan het licht te gaan? Hoe groter de schijf, hoe hoger de snelheid van de buitenste rand.

Iemand die dit idee omver kan werpen?

---

quote:

---

Op dinsdag 2 september 2003 12:20 schreef smash789 het volgende:
Stel je hebt een ENORM grote schijf in de ruimte. Deze laat je vanuit het middelpunt draaien. Uiteindelijk moet het dan toch mogelijk zijn om sneller dan het licht te gaan? Hoe groter de schijf, hoe hoger de snelheid van de buitenste rand.

Iemand die dit idee omver kan werpen?

---

EDIT:

Desnoods met een flinke nuke proberen om materiaal zoveel mogelijk snelheid te geven.

[Dit bericht is gewijzigd door smash789 op 02-09-2003 12:34]

quote:

---

Op dinsdag 2 september 2003 12:32 schreef Skimmer het volgende:

[..]

Nee, want die schijf wordt steeds zwaarder, en er is dus steeds meer energy voor nodig om hem te versnellen... uiteindelijk wordt ie te zwaar om verder te versnellen en dan zit je aan de rand nog niet op lichtsnelheid.

---

Theorie is leuk, maar praktisch niet haalbaar.

quote:

---

Op dinsdag 2 september 2003 12:33 schreef Royman het volgende:
Ik weet alleen dat er in zulke extreme situaties ook hele rare dingen gebeuren. Volgens de relativiteitstheorie staat tijd onder invloed van de zwaartekracht. De definitie van snelheid, is afstand gedeeld door tijd. Vervolgens is het zo dat door de enorme toename in massa er dus ook een veel zwaarder zwaartekracht veld onstaat die de tijd aanpast en zodoende ook de snelheid die je meet. Een ding weet ik wel, het is allemaal heel erg vaag.

---

quote:

---

Een vuurtoren wordt op de noordpool gezet en zend een lichtstraal uit. Deze lichtstraal beweegt zich met een bepaalde snelheid. Hoe verder je van de vuurtoren verwijderd bent, hoe sneller de straal beweegt. Je komt dus ergens op een punt dat deze straal sneller gaat dan het licht.

---

quote:

---

Op dinsdag 2 september 2003 12:39 schreef smash789 het volgende:
Ik lees net in een ander topic iets van een user:
[..]

Zou het licht dan afbuigen alsof je al ronddraaiend aan het rondspuiten bent met een waterpistool?

---

quote:

---

Op dinsdag 2 september 2003 12:32 schreef smash789 het volgende:
Stel je maakt op die buitenste rand één of ander systeem, dat wanneer de maximum haalbare snelheid van de schijf is bereikt, een projectiel zo hard mogelijk afschiet in de richting waarin de schijf draait. Maar dan ervoor zorgen dat dit projectiel rechtuit gaat in plaats van meedraaien in de cirkel.
Of zou dit projectiel dan nog steeds te zwaar zijn?

EDIT:

Desnoods met een flinke nuke proberen om materiaal zoveel mogelijk snelheid te geven.

---

wat je dus nodig hebt zijn deeltjes die GEEN massa hebben. Of een negatieve massa en dus alleen maar sneller dan de lichtsnelheid kunnen bewegen.

quote:

---

Op dinsdag 2 september 2003 12:42 schreef avdbree het volgende:

[..]

Nee. Licht heeft geen massa en heeft geen last van 'onze' zwaartekracht.

---

quote:

---

Nee. Licht heeft geen massa en heeft geen last van 'onze' zwaartekracht.

---

quote:

---

Op dinsdag 2 september 2003 12:20 schreef smash789 het volgende:
Stel je hebt een ENORM grote schijf in de ruimte. Deze laat je vanuit het middelpunt draaien. Uiteindelijk moet het dan toch mogelijk zijn om sneller dan het licht te gaan? Hoe groter de schijf, hoe hoger de snelheid van de buitenste rand.

Iemand die dit idee omver kan werpen?

---

Kan niet. Het universum is niet homogeen. Door sneller te draaien verander je de tijdruimte om de schijf heen waardoor je te maken krijgt met een steeds sterker worden acceleratie wat als effect heeft dat de massa lijkt toe te nemen. Op een gegeven moment heb je oneindig veel energie nodig.

Ook bij een zwart gat gebeuren deze dingen niet. Een zwart gat is ruimtetijd waarbij de dichtheid het oneindige benadert. Verder dan de benadering komt niet. Simpelweg omdat de bouwstenen en natuurwetten die dit universum tot het universum maken in een oneindige dichtheid niet meer zouden gelden. Een zwart gat zou zichzelf opheffen als die oneindige dichtheid zou worden bereikt en dat kan alleen als alle massa en energie van het universum eraan te pas zouden komen.

ET

Dit levert wel het probleem op dat de energie die je er eerst instop al zo groot moet zijn. Dat haal je al niet.

Dus neen, hoe hard je de schijf ook rond draait, de rand zal nooit de lichtsnelheid berijken. a) omdat een steeds sneller draaiende schijf steeds kleiner wordt en b) omdat de energie die je erin pompt niet afdoende is.

Bijna lichtsnelheid is echter vrij eenvoudig.

quote:

---

Op dinsdag 2 september 2003 12:58 schreef Plompzak het volgende:
bovendien hebben licht deeltjes (fotonen) wel degelijk massa. Hoe denk je anders dat een zwart gat donker blijft? De zwaartekracht is zo groot dat zelfs licht niet meer kan ontsnappen. Dat werkt alleen maar als licht massa heeft...

---

ET.

quote:

---

Op dinsdag 2 september 2003 14:51 schreef Keromane69 het volgende:
Zie ook: Kurzwaski-2 Experiment

Kan niet. Het universum is niet homogeen. Door sneller te draaien verander je de tijdruimte om de schijf heen waardoor je te maken krijgt met een steeds sterker worden acceleratie wat als effect heeft dat de massa lijkt toe te nemen. Op een gegeven moment heb je oneindig veel energie nodig.

Ook bij een zwart gat gebeuren deze dingen niet. Een zwart gat is ruimtetijd waarbij de dichtheid het oneindige benadert. Verder dan de benadering komt niet. Simpelweg omdat de bouwstenen en natuurwetten die dit universum tot het universum maken in een oneindige dichtheid niet meer zouden gelden. Een zwart gat zou zichzelf opheffen als die oneindige dichtheid zou worden bereikt en dat kan alleen als alle massa en energie van het universum eraan te pas zouden komen.

ET

---

Zodra je met zulke waardes van grootheden hebt
te maken, gelden de ons bekende wetten niet meer.
Speculatie....

quote:

---

Op dinsdag 2 september 2003 12:58 schreef Plompzak het volgende:
bovendien hebben licht deeltjes (fotonen) wel degelijk massa. Hoe denk je anders dat een zwart gat donker blijft? De zwaartekracht is zo groot dat zelfs licht niet meer kan ontsnappen. Dat werkt alleen maar als licht massa heeft...

---

quote:

---

Op donderdag 4 september 2003 00:27 schreef PvtRyan het volgende:

[..]

Fotonen hebben geen massa. Dat ze beïnvloed worden door een zwart gat is omdat een zwart gat de ruimte-tijd kromt, licht volgt een rechte lijn door de ruimte en buigt mee met de ruimte-tijd kromming.

---

quote:

---

Op dinsdag 2 september 2003 12:58 schreef smash789 het volgende:
Dus als dat licht dan sneller dan het licht zou gaan

---

quote:

---

Op donderdag 4 september 2003 09:15 schreef Pie.er het volgende:
Fotonen hebben 100% geen massa. Binas is gewoon niet relativiteitstheoriecompatibel.

---

1. E=m*c*c => als een foton geen massa zou hebben, moet je hier vermenigvuldigen met 0, en de uitkomst is dus ook nul. Terwijl fotonen (golven; licht) wel energie bezitten. Een gloeilamp geeft 95 % warmte af en 5 % licht ....
Stel: de zon staat "schuin" tussen aarde en de een ster.
Zonder zonlicht zouden we die ster (net) naast de zon kunnen zien, maar omdat het licht letterlijk wordt afgebogen door de zwaartekracht van de zon, zien wij die ster aan de andere (!) kant van de zon !

2. Een foton is echter een ook een golf. Het heeft alle karateristieke eigenschappen voor om als een golf te worden aangemerkt; frequentie, amplitude, ....
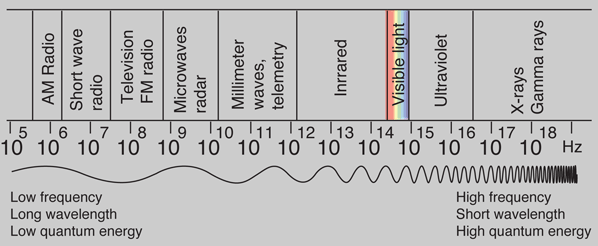
Net zoals ULF en ELF bezitten die golven een energie. Het is bekend dat bij mensen (en dieren) ELF golven het gevoel beïnvloeden... Er zijn zelfs wapens van gemaakt. Des te lager de fequentie, des te meer energie. Gamma straling zijn ook golven, en die hebben hopen energie.

En daar zit de tegenstrijdigheid: Is het een golf of een deeltje ?
Voornamelijk omdat dit twee belangerijkste, onverenigbare leerscholen zijn in de Fysica.die niet te verenigen nlijken. Daar zijn ze nl. al een tijd naar op zoek, de: "Great Unification Theory".

LijkWelEenLeraarMan, Wizard...

*dit feit kwam na voren na een heeeele lange discussie met mijn 2 wetenschappelijke chefs

quote:

---

Op woensdag 3 september 2003 20:27 schreef mechatronics het volgende:
ok, ik ben geen betá geen vwo'er zelfs geen havo'er maar kijk.

Lichtsnelheid is de hoogste snelheid hé
(onthou dat ff)
als je naast de trein gaat rennen, hou je em niet bij
trein 200 km/h jij 20km/h (jaaaa atletisch)
je zit in de trein en je rent naar voren
snelheid over de aarde, even van noord naar zuid reizend , ga je 220 km/h over de grond >> neem dit principe een hele flinke stap groter

licht gaat 3.000.000 km/s (toch?)
snelheid van het licht is, (ok, niet nu,) maar wel theoretisch al wel te halen, maar nu nog de praktijk
als je in dat ding dus, tegen de lichtsnelheid aan (niet persee vooruit, maar n grote cirkel heel snel draaiend) daarin gaat zitten, met nog zown snelle trein, jaaa bijna
dan ga je sneller als het licht eigenlijk is

zou dat betekenen dat je sneller gaat als het licht, of langzamer door de tijd reist, en misschien wel terug reist??

nou? nou ? nou? onzin zeker, kweenie

---

k denk dus, dat er iets te doen moet zijn met een schijf inderdaad, rechtlijnig is bijna niet te halen
als je nu ns energiebron vanaf aarde een laserstraal laat zenden, midden op de punt van een kegel, waaromheen een torus zit, die van die energie bruikbare energie kan maken (denk aan dat tolletje van discovery)
dan kan je al heel snel gaan,
als je dan in die schijf zelf een magneetruimte maak, die kan draaien op die energie, waardoor je de zwaartekracht minder maakt, misschien zelfs negatief , en dan vervolgens IN die schijf nog zown zelfde zet, aangedreven evt. door kernenergie...:Y

-- i have visions-- but keep on dreamin..

quote:

---

Op donderdag 4 september 2003 22:00 schreef Unstable_Element het volgende:
Leuk... een foton kan wel sneller als c maar een groepje niet... huh?! conclusie je kunt sneller als het licht, alleen geen info verplaatsen met die snelheid...

*dit feit kwam na voren na een heeeele lange discussie met mijn 2 wetenschappelijke chefs

---

Kan er me wel in vinden dat bits een massa hebben als het
dus informatiedragers zijn; 1:2 dan, want het is aan of uit ... Hmmmm ?
Geen bit, is het ontbreken van....

Sneller dan licht .... Dan moet de energie en dus de frequentie en
de amplitude van de golf zulke extremiteiten vertonen dat we het niet kunnen waarnemen, lijk mij. Dus zowel de plaats en de positie kunnen we dan niet bepalen, laat staan tegelijk. Ik moet toch meer eenduidige aanwijzingen hebben dat het kan, experimentele bewijzen, het liefst ... voor dat ik (men) kan bevatten welke wetten en theorieën regeren op dat niveau, als het al mogelijk is om daar te bestaan.... Erg hypothetisch allemaal.... Net zoals het idee van meerdere dimensies. ..

InquiringMindsWantToKnowEvenMore, Wizard

quote:

---

Op donderdag 4 september 2003 21:52 schreef TooFasForMellow het volgende:

[..]

In Binas staan wetenschappelijk feiten, that's it.

1. E=m*c*c => als een foton geen massa zou hebben, moet je hier vermenigvuldigen met 0, en de uitkomst is dus ook nul. Terwijl fotonen (golven; licht) wel energie bezitten. Een gloeilamp geeft 95 % warmte af en 5 % licht ....
Stel: de zon staat "schuin" tussen aarde en de een ster.
Zonder zonlicht zouden we die ster (net) naast de zon kunnen zien, maar omdat het licht letterlijk wordt afgebogen door de zwaartekracht van de zon, zien wij die ster aan de andere (!) kant van de zon !

2. Een foton is echter een ook een golf. Het heeft alle karateristieke eigenschappen voor om als een golf te worden aangemerkt; frequentie, amplitude, ....
Net zoals ULF en ELF bezitten die golven een energie. Het is bekend dat bij mensen (en dieren) ELF golven het gevoel beïnvloeden... Er zijn zelfs wapens van gemaakt. Des te lager de fequentie, des te meer energie. Gamma straling zijn ook golven, en die hebben hopen energie.

En daar zit de tegenstrijdigheid: Is het een golf of een deeltje ?
Voornamelijk omdat dit twee belangerijkste, onverenigbare leerscholen zijn in de Fysica.die niet te verenigen nlijken. Daar zijn ze nl. al een tijd naar op zoek, de: "Great Unification Theory".

LijkWelEenLeraarMan, Wizard...

---

___________________________________________________________
Ik neem geen verantwoordelijkheid voor de hierboven geschreven tekst.
-------------------------------------------------------------------------------------------------------

quote:

---

Op donderdag 4 september 2003 21:52 schreef TooFasForMellow het volgende:
In Binas staan wetenschappelijk feiten, that's it.

1. E=m*c*c => als een foton geen massa zou hebben, moet je hier vermenigvuldigen met 0, en de uitkomst is dus ook nul. Terwijl fotonen (golven; licht) wel energie bezitten. *blaat*

---

quote:

---

2.*blaat* Des te lager de fequentie, des te meer energie. Gamma straling zijn ook golven, en die hebben hopen energie.

---

quote:

---

Op maandag 8 september 2003 19:44 schreef Dr.Gallons het volgende:

Foton hebben geen massa (zelfs geen rustmassa). De formule die verder geldt is: E^2 = (m^2)(c^4) + (p^2)(c^2)
Hieruit kan je concluderen dat fotonen wel een impuls hebben (p) maar geen massa.

Volgens mij hebben golven met een hoge freq. (gamma straling bijv.) meer energie dan golven met een lage freq.

---

quote:

---

Op dinsdag 2 september 2003 12:42 schreef avdbree het volgende:

[..]

Nee. Licht heeft geen massa en heeft geen last van 'onze' zwaartekracht.

---

En een foton heeft toch geen massa als ie stil staat?

Ook leuk:
http://nl.wikipedia.org/wiki/Tachyon

En licht kan stil gezet worden, dus kan je zneller dan het licht bewegen, echter niet sneller dan zijn topsnelheid.

Hoop gebleir.....

Impuls zonder massa .... Lijkt me niet .....

E*2= (m*2)(c*4)+(p*2)(c*2) => E=(m*c*c) + (p*c)
Waar haal je die laatste term vandaan ?
Je ontkracht de belangerijkste formule van de vorige eeuw ?!?
Met commutatieve termen kom je op zo'n manier erg ver, ja !
.... (p*c) => {(kg*m/s)*(m/s)} => kg*m*m/s*s => .... (substantief!)
Dan hou je uieindelijk -alleen maar- massa over zonder vector.
Je zal bedoelen => E=p*c ... De "p" is een combo van m*c....
Klopt niet ! BLAAAT !!!!

Wizz )>

Ik doelde op kinetische energie.
Dus dat er relatief (!) veel energie moet woden "ingestoken"
om die golven te krijgen. Net zoals aan de andere kant van het spectrum het geval is.

Wizz

quote:

---

Op dinsdag 9 september 2003 07:54 schreef TooFasForMellow het volgende:

Hoop geblear

---

Er is een afspraak tussen wetenschappers dat licht geen massa heeft. Ze gebruiken de term massa ook heel spaarzaam en spreken eigenlijk alleen over Energie. Omdat de energie van een massief deeltje toeneemt bij grotere snelheid, spreken gewone mensen over de relativistische massa die in relatie staat tot de energie. Maar die relatie is niet de bekende formule E=mc², maar de vorm die gebaseerd is op het impulsmoment. Als je dus de energie van een foton weet dan kun je z'n impuls uitrekenen via de formule die Dr.Gallons al correct gegeven had. Het enigste wat je dus nodig hebt is de frequentie van de foton en die kun je bijvoorbeeld met een prisma bepalen. E=mc² is de foute formule, omdat hij alleen geldt bij rust!

Een foton heeft, volgens "Einstein's Special Theory of Relativity", geen (rust)massa ofwel inertia.

De theorie stelt namelijk twee belangrijke zaken:

1. Een object met rustmassa ongelijk nul kan nooit de lichtsnelheid bereiken.

2. Een object zonder rustmassa (dus m₀=0) beweegt altijd met de lichtsnelheid.

Uit beide regels afzonderlijk volgt dat een foton geen rustmassa heeft. Uit de tweede regel volgt tevens waarom de rustmassa nul is, namelijk omdat een foton bij rust niet bestaat.

De foutieve gedachte dat een foton een onmeetbaar kleine rustmasse zou hebben komt soms voort uit het feit dat een foton weldegelijk energie heeft. En als je niet de volledige formule voor deeltjesenergie van Einstein gebruikt, dan kom je tot de foute conclusie dat een foton een zeer kleine massa moet hebben:

E = m · c²

Deze formule is niet volledig en geldt alleen als het object in rust is (geen impuls heeft), maar een foton kan nooit in rust zijn, omdat het dan niet kan bestaan! Maar dat wordt vaak vergeten en je kunt dan ten onrechte stellen dat een foton een onmeetbaar kleine massa nodig heeft om energie te kunnen hebben.

De juiste (volledige) formule van Einstein is:

E = ( p² · c² + m₀² · c⁴ )^1/2

Omdat m₀ voor een foton gelijk aan nul is, komt de energie van een foton volgens Einstein als denkbeeldig deeltje voort uit zijn impuls p, zijnde het product van de relativistische deeltjesmassa m_c en de deeltjessnelheid c.

E = ± p · c

Het eerder genoemde product van m_c en c gebruiken we echter niet voor de oplossing van de volledige deeltjesenergieformule van Einstein, omdat we voor de bepaling van de niet constante (lichtfrequentie afhankelijke) m_c, dan precies dezelfde formule zouden moeten gebruiken die we juist proberen op te lossen.

We gebruiken de minder gecompliceerde formule van Planck voor de fotonenergie.

E = h · f

De energie is hierbij gelijk aan de constante van Planck maal de golffrequentie. Dit is de energieafleiding als denkbeeldige golf en in deze formule komt dus geen relativistische massa voor. Beide formules voor de energie kloppen omdat er een vaste relatie bestaat tussen de frequentie en de relativistische massa van een foton (dualiteits principe). Als een foton echter ook nog een rustmassa ongelijk nul zou hebben dan zou de laatste formule, zoals bij de berekening van de slingerfrequentie van een uurwerk, wel een massacomponent moeten bevatten.

Dit is trouwens al eeuwen geleden aangetoond. Wie handig is kan dat ook zelf doen; met een zaklamp, een vacuumstolp, een draairad van zeer licht materiaal met aan tegenoverliggende kanten witte en zwarte schoepbladen en een batterij als energiebron voor de zaklamp buiten de stolp om het draairad in de stolp op licht te laten draaien!