SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
Hello! Ik heb morgen een tentamen infinitesimaalrekening en ik loop vast op een vraag die normaal prima gaat. Ik moet de volgende differentiaalvergelijking oplossen:
f'(x) + f(x)/(x(x+1)) = x+1.
De algemene oplossing voor de homogene vergelijking (dus =0 in plaats van =x+1) heb ik al:
K(1+1/x). Nu wil ik door middel van variatie van constanten bepalen wat k(x) is voor de inhomogene vergelijking, maar dan kom ik als ik f(x)=k(x)(1+1/x) stel en dat invul in de differentiaalvergelijking uit op:
k'(x)+1/x*k'(x)+k(x)*log(x)+1/(x^2)*k(x)=x+1, waar ik niet zomaar mijn k(x) uit kan halen. Het antwoordmodel zegt dat er 'door invullen' uit volgt dat k'(x)(1+1/x)=(x+1), maar dat volgt er bij mij niet uit als ik het invul. Wat doe ik fout?
Sorry dat dit er lelijk uitziet, ik begin volgende periode pas met LaTeX...
f'(x) + f(x)/(x(x+1)) = x+1.
De algemene oplossing voor de homogene vergelijking (dus =0 in plaats van =x+1) heb ik al:
K(1+1/x). Nu wil ik door middel van variatie van constanten bepalen wat k(x) is voor de inhomogene vergelijking, maar dan kom ik als ik f(x)=k(x)(1+1/x) stel en dat invul in de differentiaalvergelijking uit op:
k'(x)+1/x*k'(x)+k(x)*log(x)+1/(x^2)*k(x)=x+1, waar ik niet zomaar mijn k(x) uit kan halen. Het antwoordmodel zegt dat er 'door invullen' uit volgt dat k'(x)(1+1/x)=(x+1), maar dat volgt er bij mij niet uit als ik het invul. Wat doe ik fout?
Sorry dat dit er lelijk uitziet, ik begin volgende periode pas met LaTeX...
De oplossing voor de homogene vergelijking is inderdaad correct.quote:Op woensdag 5 november 2014 14:11 schreef Aardappeltaart het volgende:
Hello! Ik heb morgen een tentamen infinitesimaalrekening en ik loop vast op een vraag die normaal prima gaat. Ik moet de volgende differentiaalvergelijking oplossen:
f'(x) + f(x)/(x(x+1)) = x+1.
De algemene oplossing voor de homogene vergelijking (dus =0 in plaats van =x+1) heb ik al:
K(1+1/x). Nu wil ik door middel van variatie van constanten bepalen wat k(x) is voor de inhomogene vergelijking, maar dan kom ik als ik f(x)=k(x)(1+1/x) stel en dat invul in de differentiaalvergelijking uit op:
k'(x)+1/x*k'(x)+k(x)*log(x)+1/(x^2)*k(x)=x+1, waar ik niet zomaar mijn k(x) uit kan halen. Het antwoordmodel zegt dat er 'door invullen' uit volgt dat k'(x)(1+1/x)=(x+1), maar dat volgt er bij mij niet uit als ik het invul. Wat doe ik fout?
Sorry dat dit er lelijk uitziet, ik begin volgende periode pas met LaTeX...
Je maakt nu een fout met de productregel.
Gebruik variatie van constante en we zien dat de oplossing voor de homogene vergelijking gegeven is door:
En dus:
Invullen in de oorspronkelijke differentiaalvergelijking geeft ons:
Probeer nu zelf de haakjes uit te werken en alles onder één noemer te brengen, je zult dan zien dat alle termen
Oftewel:
En dus
En met behulp van een beginvoorwaarde kan de integratieconstante c worden bepaald.
Heel erg bedankt. Frustrerend dit, een van de meest trieste fouten die ik gemaakt heb. Zoveel aan het integreren geweest dat ik 1/x differentieer naar ln(x).quote:
[..]
De oplossing voor de homogene vergelijking is inderdaad correct.
Je maakt nu een fout met de productregel.
Gebruik variatie van constante en we zien dat de oplossing voor de homogene vergelijking gegeven is door:
En dus:
Vincent heeft een budget van ¤9/per week voor een ochtend koffie met melk. Hij houdt ervan dat er 4 stukjes koffie en 1 stuk melk in zitten. Koffie kost ¤1 per 100g en melk kost ¤0,50 per 100g. Hoeveel koffie zal Vincent per week kopen en hoeveel melk zal Vincent per week kopen? Hoe zullen de antwoorden veranderen als de prijs van koffie wordt verhoogd naar ¤3,25?
Ik had allereerst de budgetlijn opgesteld:
9 - 4x - 0,50y
Het is 4x, aangezien hij 4 stukken koffie in zijn kopje doet en 1 stuk melk (Verhouding 4:1) en omdat de prijs ¤1 is kan ik dat net zo goed weglaten want 4 * x * ¤1 = 4x. Hetzelfde heb ik gedaan voor melk, waardoor ik uitkom op 0,50y.
Aangezien dit complementaire goederen zijn: x = y = u
9 - 4u - 0,50u = 0
9 - 4,5u = 0
9 = 4,5u
u = 2
Dus hij koopt 2 koffie per week en 2 melk per week.
Klopt dit?
Ik had allereerst de budgetlijn opgesteld:
9 - 4x - 0,50y
Het is 4x, aangezien hij 4 stukken koffie in zijn kopje doet en 1 stuk melk (Verhouding 4:1) en omdat de prijs ¤1 is kan ik dat net zo goed weglaten want 4 * x * ¤1 = 4x. Hetzelfde heb ik gedaan voor melk, waardoor ik uitkom op 0,50y.
Aangezien dit complementaire goederen zijn: x = y = u
9 - 4u - 0,50u = 0
9 - 4,5u = 0
9 = 4,5u
u = 2
Dus hij koopt 2 koffie per week en 2 melk per week.
Klopt dit?
De berekening lijkt me juist (aangenomen dat 1 stukje = 100 gram) maar de conclusie is dan toch 4*u = 8 koffie en 1*u = 2 melk.
hoe kom je op 8 en 2?quote:
De berekening lijkt me juist (aangenomen dat 1 stukje = 100 gram) maar de conclusie is dan toch 4*u = 8 koffie en 1*u = 2 melk.
Je bent niet helemaal nauwkeurig in wat je precies berekent, en daardoor kun je niet meer precies zien wat het juiste antwoord moet zijn. Je geeft als antwoord 2 koffie en 2 melk, maar omdat dat én niet in de verhouding is van de opgave én bij lange na geen 9 euro, had je snel kunnen zien dat het antwoord ook niet klopt.quote:
Als x het aantal blokjes koffie is, en y het aantal blokjes melk, dan weet je dat x = 4y (want 4 keer zoveel koffie dan melk).
Neem nu u het aantal 'setjes' van 4koffie+1melk, dan zijn de kosten van zo'n setje 4,50 (4x1+0,50)
Samen hooguit 9 euro, dus 2 setjes. 2 setjes is 8 koffie en 2 melk.
Opinion is the medium between knowledge and ignorance (Plato)
Kan iemand de verschillen uitleggen tussen surjectief en injectief icm functies? Ik begrijp dat het een surjectie betreft als alle elementen in A ook in B zitten, maar de link tussen functies is mij niet helemaal helder =/
Een functie is in wezen een koppeling tussen twee verzamelingen; het beeldt de ene verzameling (het domein) af op de andere (het bereik). De functie f(x) = x2 beeldt het bereik R af op (0;∞). Deze is surjectief, maar niet injectief.quote:
Kan iemand de verschillen uitleggen tussen surjectief en injectief icm functies? Ik begrijp dat het een surjectie betreft als alle elementen in A ook in B zitten, maar de link tussen functies is mij niet helemaal helder =/
Opinion is the medium between knowledge and ignorance (Plato)
Hoi, ik heb een vraag over het volgende bewijs:
Neem aan dat f en g Schwartz-functies zijn. Dan hebben we
Ik snap het argument in de laatste zin niet. Het kan zijn dat er van de lezer wordt verwacht dat hij zelf nog even in de weer gaat met Fouriertransformaties, maar dan snap ik niet waarom het noodzakelijk de convergentie van de limiet te bewijzen (de meeste bewijzen worden op die manier gedaan, en in het boek waar het bewijs uit komt worden Fouriertransformaties in hetzelfde hoofdstuk behandeld). Het bewijs is een bewerkte vorm (alleen de notatie is wat aangepast) van 'Classical Fourier Analysis' door Lukas Grafakos.
Neem aan dat f en g Schwartz-functies zijn. Dan hebben we
Ik snap het argument in de laatste zin niet. Het kan zijn dat er van de lezer wordt verwacht dat hij zelf nog even in de weer gaat met Fouriertransformaties, maar dan snap ik niet waarom het noodzakelijk de convergentie van de limiet te bewijzen (de meeste bewijzen worden op die manier gedaan, en in het boek waar het bewijs uit komt worden Fouriertransformaties in hetzelfde hoofdstuk behandeld). Het bewijs is een bewerkte vorm (alleen de notatie is wat aangepast) van 'Classical Fourier Analysis' door Lukas Grafakos.
Waarom is deze dan niet injectief?quote:
[..]
Een functie is in wezen een koppeling tussen twee verzamelingen; het beeldt de ene verzameling (het domein) af op de andere (het bereik). De functie f(x) = x2 beeldt het bereik R af op (0;∞). Deze is surjectief, maar niet injectief.
Nog een vraagje: in bovenstaande, R is nu het co-domein(ofwel bereik) en f(x) is het domein?
[ Bericht 21% gewijzigd door Stickers op 10-11-2014 20:18:34 ]
quote:Op maandag 10 november 2014 20:03 schreef Stickers het volgende:
[..]
Waarom is deze dan niet injectief?
Wellicht te simpel vraagje maar kom er niet uit:
'bij samengestelde interest (rente op rente) is 4,8% (1,048) per jaar gelijkwaardig aan 1,048^1/12, dus aan 0,39% per maand'.
Waarom mag je die 1,048 tot de macht 1/12 doen? Ik begrijp dat 1,0039 tot de macht 12 (rente op rente) uitkomt op 1,048 maar ik snap die tot de macht 1/12 niet.
Iemand?
'bij samengestelde interest (rente op rente) is 4,8% (1,048) per jaar gelijkwaardig aan 1,048^1/12, dus aan 0,39% per maand'.
Waarom mag je die 1,048 tot de macht 1/12 doen? Ik begrijp dat 1,0039 tot de macht 12 (rente op rente) uitkomt op 1,048 maar ik snap die tot de macht 1/12 niet.
Iemand?
Stel je hebt de functiequote:
[..]
Waarom is deze dan niet injectief?
Nog een vraagje: in bovenstaande, R is nu het co-domein(ofwel bereik) en f(x) is het domein?
Twaalfdemachts wortel. Dit omdat de rente per maand 12 keer met zichzelf vermenigvuldigd wordt, en dus gelijk is aan x^12.quote:
Wellicht te simpel vraagje maar kom er niet uit:
'bij samengestelde interest (rente op rente) is 4,8% (1,048) per jaar gelijkwaardig aan 1,048^1/12, dus aan 0,39% per maand'.
Waarom mag je die 1,048 tot de macht 1/12 doen? Ik begrijp dat 1,0039 tot de macht 12 (rente op rente) uitkomt op 1,048 maar ik snap die tot de macht 1/12 niet.
Iemand?
Ik snap zin 2. Alleen twaalfdemachtswortel? Hoe zit dit ook alweer? Tot de macht 1/12 is dus hetzelfde als twaalfdemachtswortel?quote:Op maandag 10 november 2014 21:55 schreef netchip het volgende:
[..]
Twaalfdemachts wortel. Dit omdat de rente per maand 12 keer met zichzelf vermenigvuldigd wordt, en dus gelijk is aan x^12.
Yep, tot de macht 1/n is hetzelfde als de n-demachts wortel.quote:
[..]
Ik snap zin 2. Alleen twaalfdemachtswortel? Hoe zit dit ook alweer? Tot de macht 1/12 is dus hetzelfde als twaalfdemachtswortel?
Ohja, dat zocht ik! Tnx!quote:
[..]
Yep, tot de macht 1/n is hetzelfde als de n-demachts wortel.
Op www.slimleren.nl staan heel veel theorieën uitgelegd! Is misschien handig 
Waarom bestaat wiskunddeeeeeeeeeeeeee
Waarom bestaat wiskunddeeeeeeeeeeeeee
Een van de rekenregels met logaritmen.quote:
Waarom is ^9 log (2x) = ^3 log (2x) / ^3 log (9)
alog b = clog b /clog a
Opinion is the medium between knowledge and ignorance (Plato)
Maar volgens rekenregel glog(a)= log (a) / log (g) kan het ook zijn log 2x / log 9 ?quote:
[..]
Een van de rekenregels met logaritmen.
alog b = clog b /clog a
Kan ook, in dat geval is het grondtal 10. Je kunt er 37log's van maken als je dat leuk vindt.quote:
[..]
Maar volgens rekenregel glog(a)= log (a) / log (g) kan het ook zijn log 2x / log 9 ?
Het voordeel van het grondtal 3 in jouw voorbeeld, is dat je weet hoeveel 3log 9 is.
Opinion is the medium between knowledge and ignorance (Plato)
Ah okey, thanksquote:
[..]
Kan ook, in dat geval is het grondtal 10. Je kunt er 37log's van maken als je dat leuk vindt.
Het voordeel van het grondtal 3 in jouw voorbeeld, is dat je weet hoeveel 3log 9 is.
Ik heb weer een opgave waar ik niet uitkom...
Stel, je hebt een gerichte, gewogen, sterk verbonden graaf G=(E, V) met een cykel C met totaal gewicht 0. We kiezen een 'startvertex' s. Bewijs dat er in die cykel een vertex v is waarvan de (kortste) afstand (afstand = totaal gewicht van de edges) van s tot v gelijk is aan de (kortste) afstand van s tot v in een pad met |V| zijden.
Dit laatste pad met lengte |V| bezoekt alle vertices een keer en ten minste 1 vertex meerdere keren. Het pad moet dus cykels bevatten, en in het bijzonder de cykel C (omdat de cykel de totale lengte/gewicht van de korste route niet verandert).
Kan iemand een tip geven?
Edit: gevonden! Uren naar iets kijken wat je niet begrijpt helpt soms toch wel, op de een of andere manier.
[ Bericht 7% gewijzigd door defineaz op 17-11-2014 02:24:41 ]
Stel, je hebt een gerichte, gewogen, sterk verbonden graaf G=(E, V) met een cykel C met totaal gewicht 0. We kiezen een 'startvertex' s. Bewijs dat er in die cykel een vertex v is waarvan de (kortste) afstand (afstand = totaal gewicht van de edges) van s tot v gelijk is aan de (kortste) afstand van s tot v in een pad met |V| zijden.
Dit laatste pad met lengte |V| bezoekt alle vertices een keer en ten minste 1 vertex meerdere keren. Het pad moet dus cykels bevatten, en in het bijzonder de cykel C (omdat de cykel de totale lengte/gewicht van de korste route niet verandert).
Kan iemand een tip geven?
Edit: gevonden! Uren naar iets kijken wat je niet begrijpt helpt soms toch wel, op de een of andere manier.
[ Bericht 7% gewijzigd door defineaz op 17-11-2014 02:24:41 ]
Als de kern van een lineaire transformatie over R of C meer bevat dan enkel de nulvector, geldt dan dat een of meer van de kolommen (of rijen) van de transformatiematrix een lineaire combinatie zijn van de overige rijen?
Ik weet niet zeker of deze vraagstelling wel volledig is. Als er ook nog cykels met negatief gewicht in zitten, dan is er helemaal geen kortste afstand!quote:
Ik heb weer een opgave waar ik niet uitkom...
Stel, je hebt een gerichte, gewogen, sterk verbonden graaf G=(E, V) met een cykel C met totaal gewicht 0. We kiezen een 'startvertex' s. Bewijs dat er in die cykel een vertex v is waarvan de (kortste) afstand (afstand = totaal gewicht van de edges) van s tot v gelijk is aan de (kortste) afstand van s tot v in een pad met |V| zijden.
Dit laatste pad met lengte |V| bezoekt alle vertices een keer en ten minste 1 vertex meerdere keren. Het pad moet dus cykels bevatten, en in het bijzonder de cykel C (omdat de cykel de totale lengte/gewicht van de korste route niet verandert).
Kan iemand een tip geven?
Edit: gevonden! Uren naar iets kijken wat je niet begrijpt helpt soms toch wel, op de een of andere manier.
Ja. Een element van de kern geeft namelijk een lineaire combinatie van de kolomvectoren die 0 oplevert. Als de coëfficiënten daarvan niet allemaal 0 zijn, dan kun je er een kiezen die niet 0 is en naar de andere kant halen.quote:
Als de kern van een lineaire transformatie over R of C meer bevat dan enkel de nulvector, geldt dan dat een of meer van de kolommen (of rijen) van de transformatiematrix een lineaire combinatie zijn van de overige rijen?
[ Bericht 0% gewijzigd door thabit op 17-11-2014 08:28:16 ]
Een laat bedankje voor deze reactie.quote:
[..]
Oriëntatie behoudende rotaties van R3 worden gegeven door SO(3). Je hebt zoals je weet een conjugatie norm op de quaternionen. En daarmee kun je laten zien dat de quaternionen met norm 1 onder de standaard vermenigvuldiging van de quaternionen een groep vormen en isomorf zijn aan SU(2) als groep. Iets soort gelijk kun je ook doen met de pure quaternionen en SO(3). Hint, laat zien dat de generende elementen van beide groepen hetzelfde gedragen onder hun eigen operatie.
Cuius rei demonstrationem mirabilem sane detexi hanc marginis exiguitas non caparet
Inderdaad. Die cykel waar ik het over had, was de cykel met het laagste gemiddelde gewicht. Dit impliceert dus dat er geen negatieve cykels zijnquote:
[..]
Ik weet niet zeker of deze vraagstelling wel volledig is. Als er ook nog cykels met negatief gewicht in zitten, dan is er helemaal geen kortste afstand!
Goede opmerking.
Hallo ik moet voor een schoolopdracht in C++ een pinbal spel namaken.
Ik snap alleen niet zo goed wanneer de bal de muur raakt.
Er staat het volgende uitgelegd:
Edit: ik denk toch wel dat a en b die vectoren zijn als ik het goed lees, echter snap ik nog steeds niet hoe ik het volgende oplos:
[ Bericht 2% gewijzigd door jatochneetoch op 19-11-2014 19:23:48 ]
Ik snap alleen niet zo goed wanneer de bal de muur raakt.
Er staat het volgende uitgelegd:
Wat zijn nou a en b in die formule? niet de twee vectoren van de muur lijkt me, want dan slaat die u nergens op.quote:A ball can be modeled as a class with a position (vector), a speed (vector),
and mass (double). A wall can be modeled as a class with two positions (vector)
(namely, start and end relative to start).
Lets consider a simple pinball field.
A collision should not be much harder: we can do some basic physics. If
the wall is considered as a line segment, a+u*b, with 0<=u<=1 and the particle trajectory as x(t)=xi+v*t, it is possible to determine if a collision
will occur; solving equation 4.4 is possible, because we have two equations (one
in x direction, one in y direction) and two unknowns (t, u).
Equeation 4.4: a+u*b = x0 + t*v
If 0<=u<=1, a collision will occur at time t. When a collision happens, the ball
will change velocity: it's velocity is simply re ected in the line representing a
ball.
Edit: ik denk toch wel dat a en b die vectoren zijn als ik het goed lees, echter snap ik nog steeds niet hoe ik het volgende oplos:
quote:2.Rewrite equation 4.4 to include the radius of the ball
3.Find the (algebraic) solution to when the wall and the ball collide
[ Bericht 2% gewijzigd door jatochneetoch op 19-11-2014 19:23:48 ]
Ik heb een vereenvoudigingsvraag.
Ik heb de volgende vergelijking:
L'x(x,y,/\)=y-2x(x/2y)+2(x/2y)=0
= y-(2x2)/2y+2x/2y
= y - x2/y + x/y
De uitwerkingen van mijn boek zeggen dat dit:
= y2 − x2 + x =0.
Zou iemand mij kunnen uitleggen hoe ik dat zo kan vereenvoudigen?
Ik heb de volgende vergelijking:
L'x(x,y,/\)=y-2x(x/2y)+2(x/2y)=0
= y-(2x2)/2y+2x/2y
= y - x2/y + x/y
De uitwerkingen van mijn boek zeggen dat dit:
= y2 − x2 + x =0.
Zou iemand mij kunnen uitleggen hoe ik dat zo kan vereenvoudigen?
Je raakt een paar snullen kwijt. Als je je administratie netjes bijhoudt dan wordt je laatste regel:quote:
Ik heb een vereenvoudigingsvraag.
Ik heb de volgende vergelijking:
L'x(x,y,/\)=y-2x(x/2y)+2(x/2y)=0
= y-(2x2)/2y+2x/2y
= y - x2/y + x/y
De uitwerkingen van mijn boek zeggen dat dit:
= y2 − x2 + x =0.
Zou iemand mij kunnen uitleggen hoe ik dat zo kan vereenvoudigen?
y - x2/y + x/y = 0.
Die kun je links en rechts vermenigvuldigen met y.
Opinion is the medium between knowledge and ignorance (Plato)
Super, bedankt!quote:
Je raakt een paar snullen kwijt. Als je je administratie netjes bijhoudt dan wordt je laatste regel:
Ken je je merkwaardige producten wel? Deze bijvoorbeeld:quote:
[ link | afbeelding ]
Weet iemand hoe je van stap 2 naar stap 3 gaat?
Verder gebruik je dat
Je krijgt bij de uitwerking van de drie kwadraten van een verschil van twee termen dan zes producten van twee kwadraten verminderd met drie dubbele producten van twee kwadraten. Dit is (was) echt brugklasalgebra. De laatste regel in je plaatje is trouwens fout, daar ontbreekt een kwadraat bij het inproduct u·v, dat moet uiteraard (u·v)² zijn.
[ Bericht 6% gewijzigd door Riparius op 21-11-2014 21:50:31 ]
Oke bedankt voor je post. Ik heb dat dus ook op die manier uitgewerkt. Alleen krijg ik dan een veel te lange som die niet gelijk is aan de de andere som. Waarschijnlijk dan een paar 'snelheids' foutjes gemaakt. Zou er nog even aan gaan zitten.quote:
[..]
Ken je je merkwaardige producten wel? Deze bijvoorbeeld:
Verder gebruik je dat
Je krijgt bij de uitwerking van de drie kwadraten van een verschil van twee termen dan zes producten van twee kwadraten verminderd met drie dubbele producten van twee kwadraten. Dit is (was) echt brugklasalgebra. De laatste regel in je plaatje is trouwens fout, daar ontbreekt een kwadraat bij het inproduct u·v, dat moet uiteraard (u·v)² zijn.
Ik kom niet uit een opgave voor speltheorie.
Gegeven is de volgende zero sum game 4x3 matrix:
(16, 12, 2)
(2, 6, 16)
(8, 8, 6)
(0, 7, 8)
De waarde van het spel, de zadelpunten en de optimale strategieën moeten gevonden worden.
Normaal gesproken zou ik de matrix reduceren tot een mx2 of 2xn matrix door te kijken naar welke strategieën gedomineerd worden. Echter is dat hier niet mogelijk. Dus hoe los ik dit op? Ik heb al gekeken naar welke mixed-strategieën gedomineerd worden maar hier kom ik niet uit.
Iemand die kan helpen?
antwoord zou moeten zijn:
Waarde van het spel = 9
optimale strategie speler 1 = (1/2, 1/2, 0, 0)
optimale strategie speler 2 = (a, (7-14a)/10, (3+4a)/10) met a<0<1/2
[ Bericht 17% gewijzigd door Knuck-les op 23-11-2014 17:58:15 ]
Gegeven is de volgende zero sum game 4x3 matrix:
(16, 12, 2)
(2, 6, 16)
(8, 8, 6)
(0, 7, 8)
De waarde van het spel, de zadelpunten en de optimale strategieën moeten gevonden worden.
Normaal gesproken zou ik de matrix reduceren tot een mx2 of 2xn matrix door te kijken naar welke strategieën gedomineerd worden. Echter is dat hier niet mogelijk. Dus hoe los ik dit op? Ik heb al gekeken naar welke mixed-strategieën gedomineerd worden maar hier kom ik niet uit.
Iemand die kan helpen?
antwoord zou moeten zijn:
Waarde van het spel = 9
optimale strategie speler 1 = (1/2, 1/2, 0, 0)
optimale strategie speler 2 = (a, (7-14a)/10, (3+4a)/10) met a<0<1/2
[ Bericht 17% gewijzigd door Knuck-les op 23-11-2014 17:58:15 ]
Dat klopt. Maar hoe los je het verder dan op? Waar komt de a (alfa) opeens vandaan bij voor de optimale strategie voor speler 2?quote:
1/2 * Rij 1 + 1/2 * Rij 2
domineert zowel rij 3 als rij 4?
Staat er geen stelling over in je boek?quote:
[..]
Dat klopt. Maar hoe los je het verder dan op? Waar komt de a (alfa) opeens vandaan bij voor de optimale strategie voor speler 2?
Ik weet alleen dat wanneer je niet verder kan vereenvoudigen je de volgende LP problemen moet oplossen
Met a_ij de entries van je matrix.
De optimale oplossingen (x1*, .., xn*) en (y1*, ..., ym*) zijn dan optimale strategieen
en x0* = y0* de waarde van het spel.
Het met de hand oplossen is een vervelend karwei, maar een computer kan het makkelijk oplossen.
Maar ik weet niet of dat hier de bedoeling van de opgave is.
Het moet inderdaad met de hand opgelost worden door middel van een grafische weergave. Hiervoor is dan ook een 2xn of mx2 matrix nodig. Echter, wanneer ik de twee onderste rijen wegstreep en die vervolgens grafisch oplos kom ik op een ander antwoord (zonder alfa) uit dan gegeven.quote:
[..]
Staat er geen stelling over in je boek?
Ik weet alleen dat wanneer je niet verder kan vereenvoudigen je de volgende LP problemen moet oplossen
[ afbeelding ]
[ afbeelding ]
Met a_ij de entries van je matrix.
De optimale oplossingen (x1*, .., xn*) en (y1*, ..., ym*) zijn dan optimale strategieen
en x0* = y0* de waarde van het spel.
Het met de hand oplossen is een vervelend karwei, maar een computer kan het makkelijk oplossen.
Maar ik weet niet of dat hier de bedoeling van de opgave is.
Ik kom niet uit een opgave over short-run marginal costs and minimum costs in the long run en ik hoop meer duidelijkheid hier te verschaffen:
De opgave:
A firm with the production function Q = F(K, L) is producing an output level of Q* at minimum costs in the long run. How will its short-run marginal cost when K is fixed compare with its short-run marginal cost when L is fixed?
Antwoord:
At the minimum-cost input bundle for producing Q*, we know that the extra output obtained
from the last dollar spent on labor is the same as the extra output obtained from the last dollar spent on capital. Thus the two short-run marginal cost curves will take the same value at Q*.
Ik snap het antwoord niet.. Hoe kunnen de twee short-run marginal costs dezelfde waarde geven op Q, ondanks dat ze verschillen (de 1 waar K vast is en de ander waar L vast is ) ?
Ik snap de gedachte/visualisatie er niet van.. Daarnaast snap ik niet wat het vetgedrukte met de vraag te maken heeft? Ik snap de regel wel, maar ik snap niet wat voor invloed het heeft op de twee short-run curves.. waardoor ze op 1 of andere manier toch dezelfde Q* geven..
Alvast bedankt.
De opgave:
A firm with the production function Q = F(K, L) is producing an output level of Q* at minimum costs in the long run. How will its short-run marginal cost when K is fixed compare with its short-run marginal cost when L is fixed?
Antwoord:
At the minimum-cost input bundle for producing Q*, we know that the extra output obtained
from the last dollar spent on labor is the same as the extra output obtained from the last dollar spent on capital. Thus the two short-run marginal cost curves will take the same value at Q*.
Ik snap het antwoord niet.. Hoe kunnen de twee short-run marginal costs dezelfde waarde geven op Q, ondanks dat ze verschillen (de 1 waar K vast is en de ander waar L vast is ) ?
Ik snap de gedachte/visualisatie er niet van.. Daarnaast snap ik niet wat het vetgedrukte met de vraag te maken heeft? Ik snap de regel wel, maar ik snap niet wat voor invloed het heeft op de twee short-run curves.. waardoor ze op 1 of andere manier toch dezelfde Q* geven..
Alvast bedankt.
Hoi, een vraagje:
Stel er is een functie MR1 = 100 - 2Q en MR2 = 60
Hoe bepaal ik de totale MR functie?
[ Bericht 4% gewijzigd door Super-B op 24-11-2014 15:23:58 ]
Stel er is een functie MR1 = 100 - 2Q en MR2 = 60
Hoe bepaal ik de totale MR functie?
[ Bericht 4% gewijzigd door Super-B op 24-11-2014 15:23:58 ]
Wat is een MR-functie? Ik ben niet zo thuis in de economie.quote:
Hoi, een vraagje:
Stel er is een functie MR1 = 10 - 2Q1 en een functie MR2 = 20 - 2Q2
Hoe bepaal ik de totale MR functie?
Opinion is the medium between knowledge and ignorance (Plato)
Marginale opbrengsten functie (Marginal Revenues).quote:
[..]
Wat is een MR-functie? Ik ben niet zo thuis in de economie.
Dan zou ik als leek zeggen dat je ze gewoon op moet tellen.quote:
[..]
Marginale opbrengsten functie (Marginal Revenues).
Opinion is the medium between knowledge and ignorance (Plato)
Dat dacht ik dus ook, maar in het boek is het snijpunt met de y-as op punt 20 en niet op punt 30.. (zoals je zou denken, na het optellen).quote:
[..]
Dan zou ik als leek zeggen dat je ze gewoon op moet tellen.
Het snijpunt van wat? De twee MR-formules hebben twee verschillende variabelen. Of zijn die toevallig op de een of andere manier afhankelijk?quote:
[..]
Dat dacht ik dus ook, maar in het boek is het snijpunt met de y-as op punt 20 en niet op punt 30.. (zoals je zou denken, na het optellen).
Opinion is the medium between knowledge and ignorance (Plato)
Is het nietquote:
[..]
Het snijpunt van wat? De twee MR-formules hebben twee verschillende variabelen. Of zijn die toevallig op de een of andere manier afhankelijk?
Q totaal = Q1 + Q2
Dus.. alles oplossen voor Q, optellen en vervolgens oplossen voor MR ?
Had de foute functie gepost... Hierbij nogmaals de goede:quote:
[..]
Het snijpunt van wat? De twee MR-formules hebben twee verschillende variabelen. Of zijn die toevallig op de een of andere manier afhankelijk?
MR1 = 100 - 2Q en MR2 = 60
Kan iemand mij aanwijzen waar ik de fout in ga:
[tex]
(x-3)^2 + x = 0
(x-3) = i*sqrt(x) v. x-3 = -i*sqrt(x)
sqrt(x) = 3 + i v. sqrt(x) = 3-i
x= (3 + i)^2 v. x = (3 - i)^2
x = 9 + 3i + -1 v x = 9 -3i + - 1
x = 8 + 3i v. x = 8 - 3i
[/tex]
[tex]
(x-3)^2 + x = 0
(x-3) = i*sqrt(x) v. x-3 = -i*sqrt(x)
sqrt(x) = 3 + i v. sqrt(x) = 3-i
x= (3 + i)^2 v. x = (3 - i)^2
x = 9 + 3i + -1 v x = 9 -3i + - 1
x = 8 + 3i v. x = 8 - 3i
[/tex]
Waarom schrijf je het kwadraat niet uit? Dan kun je de abc-formule gebruiken. Wat je nu doet is heel omslachtig en fout.quote:
Kan iemand mij aanwijzen waar ik de fout in ga:
[tex]
(x-3)^2 + x = 0
(x-3) = i*sqrt(x) v. x-3 = -i*sqrt(x)
sqrt(x) = 3 + i v. sqrt(x) = 3-i
x= (3 + i)^2 v. x = (3 - i)^2
x = 9 + 3i + -1 v x = 9 -3i + - 1
x = 8 + 3i v. x = 8 - 3i
[/tex]
Als je wil weten waar je de fout ingaat: van de tweede naar de derde regel klopt niet, je deelt beide kanten door sqrt(x), maar je vergeet 3 ook hierdoor te delen.
Oh jaquote:
[..]
Waarom schrijf je het kwadraat niet uit? Dan kun je de abc-formule gebruiken. Wat je nu doet is heel omslachtig en fout.
Als je wil weten waar je de fout ingaat: van de tweede naar de derde regel klopt niet, je deelt beide kanten door sqrt(x), maar je vergeet 3 ook hierdoor te delen.
. Dankje!
Als ik een rechte lijn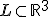 
en twee punten 
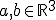heb, en ik ga deze twee punten loodrecht projecteren op de lijn L (gemakshalve noem ik de projecties a' en b' resp.).
Intuïtief zou ik dan zeggen dat:
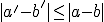
Klopt dit inderdaad? Zo ja, hoe zo ik dit kunnen bewijzen?
Moet ik de directe formule voor een projectie gebruiken, of is het simpelweg een kwestie van de driehoeksongelijkheid toepassen?
Ik zie het zo snel niet in, hulp zou gewaardeerd worden.
Intuïtief zou ik dan zeggen dat:
Klopt dit inderdaad? Zo ja, hoe zo ik dit kunnen bewijzen?
Moet ik de directe formule voor een projectie gebruiken, of is het simpelweg een kwestie van de driehoeksongelijkheid toepassen?
Ik zie het zo snel niet in, hulp zou gewaardeerd worden.
Dit moet niet zo moeilijk zijn.quote:
Als ik een rechte lijn
Intuïtief zou ik dan zeggen dat:
Klopt dit inderdaad? Zo ja, hoe zo ik dit kunnen bewijzen?
Moet ik de directe formule voor een projectie gebruiken, of is het simpelweg een kwestie van de driehoeksongelijkheid toepassen?
Ik zie het zo snel niet in, hulp zou gewaardeerd worden.
Schrijf a' en b' als a en b en c, gebruik de driehoeksongelijkheid en volgens mij ben je er dan al.
[...] onzin
[ Bericht 20% gewijzigd door t4rt4rus op 25-11-2014 20:02:39 ]
Ik begrijp niet wat je hier doet. Er hoeft helemaal geen punt X op lijn ℓ te liggen waarvan de afstand tot de oorsprong gelijk is aan 1 en ook hoeven de loodrechte projecties A' en B' van A en B op ℓ helemaal niet collineair te zijn met de oorsprong.quote:
Ik dacht je neemt de eenheidsvector c op de lijn L, dan is de projectie van a op L, a', gegeven door a' = (a.c)c.quote:
[..]
Ik begrijp niet wat je hier doet. Er hoeft helemaal geen punt X op lijn ℓ te liggen waarvan de afstand tot de oorsprong gelijk is aan 1 en ook hoeven de loodrechte projecties A' en B' van A en B op ℓ helemaal niet collineair te zijn met de oorsprong.
Is dit dan wat beter?
Waarin
Stel de lijn L gaat door de oorsprong.
Neem een vector c parallel aan lijn L.
Dan is de projectie van a op L geven door
En de projectie van b door
Waaruit volgt dat
[ Bericht 7% gewijzigd door t4rt4rus op 25-11-2014 22:03:46 ]
Bedankt voor je reactie, maar volgens mij gaat dit niet werken...quote:
[..]
Dit moet niet zo moeilijk zijn.
Schrijf a' en b' als a en b en c, gebruik de driehoeksongelijkheid en volgens mij ben je er dan al.
Je definieert nu c als een verzameling, hoe is dan het inproduct van a met c gedefinieerd?
Tevens, de verzameling c kan ook leeg zijn, je kunt namelijk jouw c opvatten als de doorsnede van de lijn L met de bol met straal 1. Die doorsnede kan leeg zijn.
Edit: Sorry, ik zie nu dat Riparius dit al had opgemerkt en je hier al op hebt gereageerd, even lezen.
Nogmaals edit:
Je beschouwt dus de eenheidsvector c die de richting van de lijn L bepaalt.
Kom je dan niet in de problemen zodra L niet door de oorsprong gaat?
Derde update:
Nogmaals bedankt voor je herziene uitwerking, echter ga je er mijns inziens nu (onterecht) vanuit dat
[ Bericht 5% gewijzigd door Hahatsjoe op 25-11-2014 20:09:09 ]
quote:
[..]
Bedankt voor je reactie, maar volgens mij gaat dit niet werken...
Je definieert nu c als een verzameling, hoe is dan het inproduct van a met c gedefinieerd?
Tevens, de verzameling c kan ook leeg zijn, je kunt namelijk jouw c opvatten als de doorsnede van de lijn L met de bol met straal 1. Die doorsnede kan leeg zijn.
Edit: Sorry, ik zie nu dat Riparius dit al had opgemerkt en je hier al op hebt gereageerd, even lezen.
Nogmaals edit:
Je beschouwt dus de eenheidsvector c die de richting van de lijn L bepaalt.
Kom je dan niet in de problemen zodra L niet door de oorsprong gaat?
Derde update:
Nogmaals bedankt voor je herziene uitwerking, echter ga je er mijns inziens nu (onterecht) vanuit dat. Waarom mag je dit zeggen?
Voor een scalar a geldt toch |x c| = |x| |c| ?
[ Bericht 4% gewijzigd door t4rt4rus op 25-11-2014 21:17:07 ]
Ja.quote:
[..]
Voor een scalar a geldt toch |a c| = |a| |c| ?
Ik snap alleen niet hoe je nu precies die c introduceert. Volgens mij bedoel je dat je de lijn als het ware parametriseerd.
Immers, elk punt op de lijn L kun je schrijven als
waarbij r de richtingsvector is en s de steunvector (en t is de parameter).
Definieer je nu
Ik ben gewoon (namen van) lijnen met kleine letters aan te geven en (namen van) punten met hoofdletters, dus dat zal ik hier ook doen. We hebben in R3 een rechte ℓ en tevens twee punten A en B waarvan we veronderstellen dat deze verschillend zijn. Laten verder A' en B' de loodrechte projecties zijn van resp. A en B op ℓ. Gevraagd wordt nu te bewijzen dat d(A', B') ≤ d(A, B).quote:
Als ik een rechte lijn
Intuïtief zou ik dan zeggen dat:
Klopt dit inderdaad? Zo ja, hoe zou ik dit kunnen bewijzen?
Moet ik de directe formule voor een projectie gebruiken, of is het simpelweg een kwestie van de driehoeksongelijkheid toepassen?
Ik zie het zo snel niet in, hulp zou gewaardeerd worden.
Als A' = B' dan is er niets meer te bewijzen, zodat we A' ≠ B' mogen veronderstellen. Laten we nu de vectoren OA, OB, OA', OB' aangeven met resp. a, b, a', b', dan is
ℓ: v = a' + λ(b' − a')
een vectorvoorstelling van de rechte ℓ. Liggen de punten A en B niet op ℓ, dan staan de lijnstukken AA' en BB' beide loodrecht op lijnstuk A'B', zodat
(1) (a' − a)·(b' − a') = 0
en
(2) (b' − b)·(b' − a') = 0
Merk op dat (1) en (2) eveneens gelden als de punten A en of B wel op ℓ liggen, aangezien a' − a resp. b' − b dan de nulvector is. Uit (1) en (2) volgt nu
(3) a'·(b' − a') = a·(b' − a')
en
(4) b'·(b' − a') = b·(b' − a')
en daarmee
(5) (b' − a')·(b' − a') = (b − a)·(b' − a')
zodat
(6) | b' − a' |2 = | b − a | · | b' − a' | · | cos ∠(b − a, b' − a') |
Maar nu is A' ≠ B' zodat | b' − a' | ≠ 0 en dus hebben we
(7) | b' − a' | = | b − a | · | cos ∠(b − a, b' − a') |
en daarmee
(8) | b' − a' | ≤ | b − a |
QED
[ Bericht 0% gewijzigd door Riparius op 27-11-2014 17:42:50 ]
Je bent zo te zien nog steeds in de war. Eerst was je a een vector, en nu is het weer een scalar. En het is onduidelijk wat je nu wil met die genormeerde richtingsvector van de rechte, die heb je helemaal niet nodig.quote:
[..]
Ja, zo ja.
Sorry was net even in de war.
Oh die laatste zin van mij had niet veel met de rest te maken.quote:
[..]
Je bent zo te zien nog steeds in de war. Eerst was je a een vector, en nu is het weer een scalar. En het is onduidelijk wat je nu wil met die genormeerde richtingsvector van de rechte, die heb je helemaal niet nodig.
In de rest is a gewoon een vector.
Maar het ging hier toch om een projectie van de vectoren a en b op de lijn L?
Nemen we een vector c parallel met de lijn L dan zijn de projecties gegeven door
x' = (x.ĉ)ĉ
Je kunt volgens mij die vraag makkelijk bewijzen in R^2 en dan veralgemeniseren naar R^3 en zo naar R^n.
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Nee, en dit is kennelijk je misverstand. Het gaat om de loodrechte projecties A' en B' van twee punten A resp. B op een rechte ℓ en om te bewijzen dat dan d(A', B') ≤ d(A, B).quote:
[..]
Oh die laatste zin van mij had niet veel met de rest te maken.
In de rest is a gewoon een vector.
Maar het ging hier toch om een projectie van de vectoren a en b op de lijn L?
Nemen we een vector c parallel met de lijn L dan zijn de projecties gegeven door
x' = (x.ĉ)ĉ
En laat ik dat in feite al hebben gedaan.quote:
Je kunt volgens mij die vraag makkelijk bewijzen in R^2 en dan veralgemeniseren naar R^3 en zo naar R^n.
Is dat niet gewoon hetzelfde als de projectie van de vectoren a en b op een vector c als we de lijn L door de oorsprong laten gaan?quote:
[..]
Nee, en dit is kennelijk je misverstand. Het gaat om de loodrechte projecties A' en B' van twee punten A resp. B op een rechte ℓ en om te bewijzen dat dan d(A', B') ≤ d(A, B).
De problemen zijn dan equivalent aan elkaar.
Het punt is dat de gegeven rechte ℓ niet door de oorsprong hoeft te gaan. Je lijkt ook niet te begrijpen dat de vier punten A, B, A' en B' niet in één vlak hoeven te liggen. Heb je mijn uitwerking bestudeerd en begrijp je deze ook?quote:
[..]
Is dat niet gewoon hetzelfde als de projectie van de vectoren a en b op een vector c als we de lijn L door de oorsprong laten gaan?
De problemen zijn dan equivalent aan elkaar.
Gelukkig maar.quote:
Ontzettend bedankt voor je uitwerking Riparius, het is volledig duidelijk!
Dan verander je de oorsprong zodat dat wel het geval is. Dat verandert toch niks aan het probleem?quote:
[..]
Het punt is dat de gegeven rechte ℓ niet door de oorsprong hoeft te gaan.
Waarom zou ik dat niet begrijpen?quote:Je lijkt ook niet te begrijpen dat de vier punten A, B, A' en B' niet in één vlak hoeven te liggen.
Nee nog niet.quote:Heb je mijn uitwerking bestudeerd en begrijp je deze ook?
Maar wat mankeert er aan mijn kladwerk?
-edit- Als ik aangeef dat we lijn L door de oorsprong laten gaan
-edit- Ik heb even heel snel naar jou uitwerking gekeken en snap wat je doet.quote:Stel de lijn L gaat door de oorsprong.
Neem een vector c parallel aan lijn L.
Dan is de projectie van a op L geven door
En de projectie van b door
Waaruit volgt dat
[ Bericht 9% gewijzigd door t4rt4rus op 25-11-2014 22:05:22 ]
De middelwaardestelling geldt in het algemeen niet voor (reguliere) krommen in R^n, toch? Ik kan namelijk zo wel enkele krommen bedenken in R^3 waarvoor deze stelling niet opgaat.
Ik zit echter in m'n maag met R^2, want ik kan hier geen juist tegenvoorbeeld voor bedenken. Ik krijg nu zelfs het vermoeden dat de stelling wel geldt in R^2.
Formeler gesproken, ik wil dus de volgende stelling bewijzen of ontkrachten:
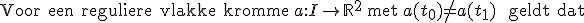
![\exists t \in [t_0, t_1] \ \text{zodanig dat} \ a'(t} \ \text{parallel is met de lijn} \ L \ \text{tussen} \ a(t_0) \ \text{en} \ a(t_1)](https://forum.fok.nl/lib/mimetex.cgi?%5Cexists%20t%20%5Cin%20%5Bt_0%2C%20t_1%5D%20%20%5C%20%5Ctext%7Bzodanig%20dat%7D%20%5C%20a%27%28t%7D%20%5C%20%5Ctext%7Bparallel%20is%20met%20de%20lijn%7D%20%5C%20L%20%5C%20%5Ctext%7Btussen%7D%20%5C%20a%28t_0%29%20%5C%20%5Ctext%7Ben%7D%20%5C%20a%28t_1%29%20)
.
Gaat het bewijs geheel analoog als het bewijs van de middelwaardestelling (uit de calculus)?
Ik zit echter in m'n maag met R^2, want ik kan hier geen juist tegenvoorbeeld voor bedenken. Ik krijg nu zelfs het vermoeden dat de stelling wel geldt in R^2.
Formeler gesproken, ik wil dus de volgende stelling bewijzen of ontkrachten:
Gaat het bewijs geheel analoog als het bewijs van de middelwaardestelling (uit de calculus)?
( 2log(p2-1) / 2log(4) ) - 2log(p+3) = (1/2)
2log(p2-1) - 2 * 2log(p+3) = 1
Kan iemand mij deze stap uitleggen? Ik kom er niet uit
2log(p2-1) - 2 * 2log(p+3) = 1
Kan iemand mij deze stap uitleggen? Ik kom er niet uit
Beide kanten zijn vermenigvuldigd met 2.quote:
( 2log(p2-1) / 2log(4) ) - 2log(p+3) = (1/2)
2log(p2-1) - 2 * 2log(p+3) = 1
Kan iemand mij deze stap uitleggen? Ik kom er niet uit
Merk op dat 2log (4) = 2 want 22 = 4.
Ik veronderstel dat je hier (x'(t), y'(t)) bedoelt met a'(t) als a(t) = (x(t), y(t)). De stelling die je wil bewijzen is in zijn algemeenheid niet waar. Wat je hier hebt is in feite de (gegeneraliseerde) middelwaardestelling van Cauchy die je wellicht bekend is omdat deze wordt gebruikt bij het bewijs van de regel van L'Hôpital.quote:
De middelwaardestelling geldt in het algemeen niet voor (reguliere) krommen in R^n, toch? Ik kan namelijk zo wel enkele krommen bedenken in R^3 waarvoor deze stelling niet opgaat.
Ik zit echter in m'n maag met R^2, want ik kan hier geen juist tegenvoorbeeld voor bedenken. Ik krijg nu zelfs het vermoeden dat de stelling wel geldt in R^2.
Formeler gesproken, ik wil dus de volgende stelling bewijzen of ontkrachten:.
Gaat het bewijs geheel analoog als het bewijs van de middelwaardestelling (uit de calculus)?
Betreffende je eerste zin, dat bedoel ik inderdaad. Ik had dat inderdaad voor de volledigheid op moeten merken.quote:
[..]
Ik veronderstel dat je hier (x'(t), y'(t)) bedoelt met a'(t) als a(t) = (x(t), y(t)). De stelling die je wil bewijzen is in zijn algemeenheid niet waar. Wat je hier hebt is in feite de (gegeneraliseerde) middelwaardestelling van Cauchy die je wellicht bekend is omdat deze wordt gebruikt bij het bewijs van de regel van L'Hôpital.
Ik kende deze stelling van Cauchy nog niet, bedankt voor het posten! Als ik het goed begrijp geldt de stelling dus wel voor R^2?
Nee, in de vorm waarin jij de stelling formuleert is deze niet algemeen geldig. In het Wikipedia artikel wordt een tegenvoorbeeld gegeven. De curve met als parametervoorstellingquote:
[..]
Betreffende je eerste zin, dat bedoel ik inderdaad. Ik had dat inderdaad voor de volledigheid op moeten merken.
Ik kende deze stelling van Cauchy nog niet, bedankt voor het posten! Als ik het goed begrijp geldt de stelling dus wel voor R^2?
x(t) = t3
y(t) = 1 − t2
waarbij we t het interval [−1, 1] laten doorlopen heeft als beginpunt (−1, 0) en als eindpunt (1, 0) maar deze curve heeft nergens een horizontale raaklijn. Check.
Bedankt voor je reactie.quote:
[..]
Nee, in de vorm waarin jij de stelling formuleert is deze niet algemeen geldig. In het Wikipedia artikel wordt een tegenvoorbeeld gegeven. De curve met als parametervoorstelling
x(t) = t3
y(t) = 1 − t2
waarbij we t het interval [−1, 1] laten doorlopen heeft als beginpunt (−1, 0) en als eindpunt (1, 0) maar deze curve heeft nergens een horizontale raaklijn. Check.
Echter, met de eis dat het een reguliere curve is, dus
Ah ja, inderdaad, dat had ik over het hoofd gezien in je formulering. In bovenstaande parametervoorstelling zijn x'(t) en y'(t) beide 0 voor t = 0.quote:
[..]
Bedankt voor je reactie.
Echter, met de eis dat het een reguliere curve is, dus, klopt het toch wel?
Beetje laat, maar hier alsnog een reply. In het minimale punt van de LAC (Long-term average costs) snijdt de MC-lijn met de LAC. Dus daardoor weet je dat de marginale kosten van labour en capital gelijk zijn in dat punt.quote:
Ik kom niet uit een opgave over short-run marginal costs and minimum costs in the long run en ik hoop meer duidelijkheid hier te verschaffen:
De opgave:
A firm with the production function Q = F(K, L) is producing an output level of Q* at minimum costs in the long run. How will its short-run marginal cost when K is fixed compare with its short-run marginal cost when L is fixed?
Antwoord:
At the minimum-cost input bundle for producing Q*, we know that the extra output obtained
from the last dollar spent on labor is the same as the extra output obtained from the last dollar spent on capital. Thus the two short-run marginal cost curves will take the same value at Q*.
Ik snap het antwoord niet.. Hoe kunnen de twee short-run marginal costs dezelfde waarde geven op Q, ondanks dat ze verschillen (de 1 waar K vast is en de ander waar L vast is ) ?
Ik snap de gedachte/visualisatie er niet van.. Daarnaast snap ik niet wat het vetgedrukte met de vraag te maken heeft? Ik snap de regel wel, maar ik snap niet wat voor invloed het heeft op de twee short-run curves.. waardoor ze op 1 of andere manier toch dezelfde Q* geven..
Alvast bedankt.
Goedemorgen allen,
Ik heb een vraag over de afgeleide van een functie waar ik niet bekend mee ben en ik hoop dat iemand mij uit de brand kan helpen. :
F(K,L) = min(aK,bL)
De afgeleiden die ik moet berekenen zijn: d F(K,L)/ d K en d F(K,L)/ d L
Alvast bedankt.
Ik heb een vraag over de afgeleide van een functie waar ik niet bekend mee ben en ik hoop dat iemand mij uit de brand kan helpen.
:F(K,L) = min(aK,bL)
De afgeleiden die ik moet berekenen zijn: d F(K,L)/ d K en d F(K,L)/ d L
Alvast bedankt.
quote:
Goedemorgen allen,
Ik heb een vraag over de afgeleide van een functie waar ik niet bekend mee ben en ik hoop dat iemand mij uit de brand kan helpen.
F(K,L) = min(aK,bL)
De afgeleiden die ik moet berekenen zijn: d F(K,L)/ d K en d F(K,L)/ d L
Alvast bedankt.
Probeer dat te gebruiken. Dan hoef je alleen nog maar op te letten waar de functie niet differentieerbaar is.
Oke hartstikke bedankt!quote:
[..]
Probeer dat te gebruiken. Dan hoef je alleen nog maar op te letten waar de functie niet differentieerbaar is.
Nog een vraag:
Wat is de afgeleide naar K en L (dQ/dK en dQ/dL) van de volgende functie?:
Ik had het allereerst herschreven tot:
2L * k1/2 * L 1/2
Dus:
2L3/2 * k1/2
dQ/dK = L3/2 * K -1/2
dQ/dL = 3L1/2 * K 1/2
Het antwoordenboek zegt echter wat anders:
Jij hebt het goed. Het antwoordenboek is in dit geval fout.quote:
[..]
Het antwoordenboek zegt echter wat anders:
[ afbeelding ]
quote:
[..]
Jij hebt het goed. Het antwoordenboek is in dit geval fout.
Deze antwoorden kloppen dus niet?
Ik vraag het maar voor de zekerheid, want ik begon, na een uur bezig te zijn, aan mijzelf te twijfelen of ik nou niet fout bezig was..
Ik kom niet uit een bewijsopgave.
Zij V ⊂ R^5 de deelruimte die gegeven wordt door de vergelijking x1+x2+x3−x4−x5 = 0.
Bewijs dat V een lineaire deelruimte is, bepaal de dimensie van V en bepaal een
basis (toon ook aan dat dit inderdaad een basis is).
welke assumpties heb ik nodig om dit bewijs te kunnen leveren? Het begrip lineaire deelruimte is nog redelijk abstract voor mij en uit de literatuur die ik heb kan ik ook niet veel opmaken. Iemand die mij op weg kan helpen?
Zij V ⊂ R^5 de deelruimte die gegeven wordt door de vergelijking x1+x2+x3−x4−x5 = 0.
Bewijs dat V een lineaire deelruimte is, bepaal de dimensie van V en bepaal een
basis (toon ook aan dat dit inderdaad een basis is).
welke assumpties heb ik nodig om dit bewijs te kunnen leveren? Het begrip lineaire deelruimte is nog redelijk abstract voor mij en uit de literatuur die ik heb kan ik ook niet veel opmaken. Iemand die mij op weg kan helpen?
Heb je uberhaupt iets geprobeerd?quote:
Ik kom niet uit een bewijsopgave.
Zij V ⊂ R^5 de deelruimte die gegeven wordt door de vergelijking x1+x2+x3−x4−x5 = 0.
Bewijs dat V een lineaire deelruimte is, bepaal de dimensie van V en bepaal een
basis (toon ook aan dat dit inderdaad een basis is).
welke assumpties heb ik nodig om dit bewijs te kunnen leveren? Het begrip lineaire deelruimte is nog redelijk abstract voor mij en uit de literatuur die ik heb kan ik ook niet veel opmaken. Iemand die mij op weg kan helpen?
De opgave zegt dat je moet bewijzen dat een deelruimte lineair is. Wanneer een ruimte lineair is, zou in je dictaat/boek moeten staan, maar als je het even niet kan vinden kan je het ook prima googelen. Er is gewoon een rij definities waar een ruimte aan moet voldoen om lineair te zijn. Je weet als het goed is dat R5 (of, algemener, Rn, voor elk natuurlijk getal n) een vectorruimte (wat een ander woord is voor een lineaire ruimte) is, dat helpt bij veel voorwaarden die je moet bewijzen.
Kijk maar even hoe ver je nu komt. Mocht je er nog niet uitkomen, help ik je graag verder als je wat duidelijker probeert aan te geven wat je probleem is.
[ Bericht 7% gewijzigd door defineaz op 30-11-2014 17:22:13 ]
Ik moet een bewijs presenteren, waarbij het resultaat van de volgende oefening wordt gebruikt. Ik kom er niet uit:
q is overigens groter of gelijk aan 1.
Ik heb geprobeerd de integraal over Rn op verschillende manieren om te schrijven. De meest veelbelovende manier leek me om de integraal over Rn als een integraal over een bol te schrijven, en het limiet te nemen als de straal van de bol naar oneindig gaat. In dit geval moet je ofwel een dubbele limiet nemen, of een straal nemen die afhangt van h.
Het lijkt me intuitief een goed idee om de bol B(h/2, |h|) te nemen en deze bol te splitsen in de bollen
A := B(0, |h|/2)
B := B(h, |h|/2)
en de rest
C := B(h/2, |h|) \ (A U B)
Volgens mij zou de integraal over C naar 0 moeten gaan als |h| naar oneindig gaat.
Je kan nu zeggen dat |x| en |x + h| allebei groter zijn dan |h|/2 in de integraal over C (anders zit x namelijk in A of B). Het lukt me alleen niet om hier nuttige afschattingen mee te maken (wat weer te maken heeft met de macht q in de integraal.
Enige tips zijn welkom! De opgave is 2.5.1 uit 'Classical Fourier Analysis' van Lukas Grafakos (lichtelijk omgeschreven).
q is overigens groter of gelijk aan 1.
Ik heb geprobeerd de integraal over Rn op verschillende manieren om te schrijven. De meest veelbelovende manier leek me om de integraal over Rn als een integraal over een bol te schrijven, en het limiet te nemen als de straal van de bol naar oneindig gaat. In dit geval moet je ofwel een dubbele limiet nemen, of een straal nemen die afhangt van h.
Het lijkt me intuitief een goed idee om de bol B(h/2, |h|) te nemen en deze bol te splitsen in de bollen
A := B(0, |h|/2)
B := B(h, |h|/2)
en de rest
C := B(h/2, |h|) \ (A U B)
Volgens mij zou de integraal over C naar 0 moeten gaan als |h| naar oneindig gaat.
Je kan nu zeggen dat |x| en |x + h| allebei groter zijn dan |h|/2 in de integraal over C (anders zit x namelijk in A of B). Het lukt me alleen niet om hier nuttige afschattingen mee te maken (wat weer te maken heeft met de macht q in de integraal.
Enige tips zijn welkom! De opgave is 2.5.1 uit 'Classical Fourier Analysis' van Lukas Grafakos (lichtelijk omgeschreven).
ah zie het nu. Dat zijn dus deze eigenschappen:quote:
[..]
Heb je uberhaupt iets geprobeerd?
De opgave zegt dat je moet bewijzen dat een deelruimte lineair is. Wanneer een ruimte lineair is, zou in je dictaat/boek moeten staan, maar als je het even niet kan vinden kan je het ook prima googelen. Er is gewoon een rij definities waar een ruimte aan moet voldoen om lineair te zijn. Je weet als het goed is dat R5 (of, algemener, Rn, voor elk natuurlijk getal n) een vectorruimte (wat een ander woord is voor een lineaire ruimte) is, dat helpt bij veel voorwaarden die je moet bewijzen.
Kijk maar even hoe ver je nu komt. Mocht je er nog niet uitkomen, help ik je graag verder als je wat duidelijker probeert aan te geven wat je probleem is.
1. Als x ∈ W en y ∈ W, dan geldt x + y ∈ W
2. Als x ∈ W en λ ∈ R, dan geldt λx ∈ W.
3. De nulvector 0 is bevat in W.
alleen hoe is dit toe te passen op de opgave? De derde stelling is simpel, maar wat wordt precies bedoeld met de eerste en tweede stelling?
Zij x = (x1, x2, x3, x4, x5) ∈ W en y = (y1, y2, y3, y4, y5) ∈ W. Dan x1+x2+x3−x4−x5 = 0 en y1+y2+y3−y4−y5 = 0.quote:
alleen hoe is dit toe te passen op de opgave? De derde stelling is simpel, maar wat wordt precies bedoeld met de eerste en tweede stelling?
Uit die twee vergelijkingen volgt x1+x2+x3−x4−x5 + y1+y2+y3−y4−y5 = (x1+y1)+(x2+y2)+(x3+y3)−(x4+y4)−(x5+y5) = 0.
Nu jij weer.
Ik zie één vergelijking met twee onbekenden. Jij ook?quote:
9 - Q2/2 = 9 - Q1/2
Hoe los je dit op? Q2 = productie van bedrijf 2 en Q1 = productie van bedrijf 1.
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Opinion is the medium between knowledge and ignorance (Plato)
quote:
[..]
Ik zie één vergelijking met twee onbekenden. Jij ook?Q2 = Q - Q1SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
Q1 = Q - Q2
Waar Q = Total Quantity..
Bedoel je dit?
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |