SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Dan zou ik als leek zeggen dat je ze gewoon op moet tellen.quote:Op maandag 24 november 2014 15:16 schreef Super-B het volgende:
[..]
Marginale opbrengsten functie (Marginal Revenues).
Opinion is the medium between knowledge and ignorance (Plato)
Dat dacht ik dus ook, maar in het boek is het snijpunt met de y-as op punt 20 en niet op punt 30.. (zoals je zou denken, na het optellen).quote:
[..]
Dan zou ik als leek zeggen dat je ze gewoon op moet tellen.
Het snijpunt van wat? De twee MR-formules hebben twee verschillende variabelen. Of zijn die toevallig op de een of andere manier afhankelijk?quote:
[..]
Dat dacht ik dus ook, maar in het boek is het snijpunt met de y-as op punt 20 en niet op punt 30.. (zoals je zou denken, na het optellen).
Opinion is the medium between knowledge and ignorance (Plato)
Is het nietquote:
[..]
Het snijpunt van wat? De twee MR-formules hebben twee verschillende variabelen. Of zijn die toevallig op de een of andere manier afhankelijk?
Q totaal = Q1 + Q2
Dus.. alles oplossen voor Q, optellen en vervolgens oplossen voor MR ?
Had de foute functie gepost... Hierbij nogmaals de goede:quote:
[..]
Het snijpunt van wat? De twee MR-formules hebben twee verschillende variabelen. Of zijn die toevallig op de een of andere manier afhankelijk?
MR1 = 100 - 2Q en MR2 = 60
Kan iemand mij aanwijzen waar ik de fout in ga:
[tex]
(x-3)^2 + x = 0
(x-3) = i*sqrt(x) v. x-3 = -i*sqrt(x)
sqrt(x) = 3 + i v. sqrt(x) = 3-i
x= (3 + i)^2 v. x = (3 - i)^2
x = 9 + 3i + -1 v x = 9 -3i + - 1
x = 8 + 3i v. x = 8 - 3i
[/tex]
[tex]
(x-3)^2 + x = 0
(x-3) = i*sqrt(x) v. x-3 = -i*sqrt(x)
sqrt(x) = 3 + i v. sqrt(x) = 3-i
x= (3 + i)^2 v. x = (3 - i)^2
x = 9 + 3i + -1 v x = 9 -3i + - 1
x = 8 + 3i v. x = 8 - 3i
[/tex]
Waarom schrijf je het kwadraat niet uit? Dan kun je de abc-formule gebruiken. Wat je nu doet is heel omslachtig en fout.quote:
Kan iemand mij aanwijzen waar ik de fout in ga:
[tex]
(x-3)^2 + x = 0
(x-3) = i*sqrt(x) v. x-3 = -i*sqrt(x)
sqrt(x) = 3 + i v. sqrt(x) = 3-i
x= (3 + i)^2 v. x = (3 - i)^2
x = 9 + 3i + -1 v x = 9 -3i + - 1
x = 8 + 3i v. x = 8 - 3i
[/tex]
Als je wil weten waar je de fout ingaat: van de tweede naar de derde regel klopt niet, je deelt beide kanten door sqrt(x), maar je vergeet 3 ook hierdoor te delen.
Oh jaquote:
[..]
Waarom schrijf je het kwadraat niet uit? Dan kun je de abc-formule gebruiken. Wat je nu doet is heel omslachtig en fout.
Als je wil weten waar je de fout ingaat: van de tweede naar de derde regel klopt niet, je deelt beide kanten door sqrt(x), maar je vergeet 3 ook hierdoor te delen.
. Dankje!
Als ik een rechte lijn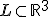 
en twee punten 
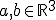heb, en ik ga deze twee punten loodrecht projecteren op de lijn L (gemakshalve noem ik de projecties a' en b' resp.).
Intuïtief zou ik dan zeggen dat:
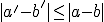
Klopt dit inderdaad? Zo ja, hoe zo ik dit kunnen bewijzen?
Moet ik de directe formule voor een projectie gebruiken, of is het simpelweg een kwestie van de driehoeksongelijkheid toepassen?
Ik zie het zo snel niet in, hulp zou gewaardeerd worden.
Intuïtief zou ik dan zeggen dat:
Klopt dit inderdaad? Zo ja, hoe zo ik dit kunnen bewijzen?
Moet ik de directe formule voor een projectie gebruiken, of is het simpelweg een kwestie van de driehoeksongelijkheid toepassen?
Ik zie het zo snel niet in, hulp zou gewaardeerd worden.
Dit moet niet zo moeilijk zijn.quote:
Als ik een rechte lijn
Intuïtief zou ik dan zeggen dat:
Klopt dit inderdaad? Zo ja, hoe zo ik dit kunnen bewijzen?
Moet ik de directe formule voor een projectie gebruiken, of is het simpelweg een kwestie van de driehoeksongelijkheid toepassen?
Ik zie het zo snel niet in, hulp zou gewaardeerd worden.
Schrijf a' en b' als a en b en c, gebruik de driehoeksongelijkheid en volgens mij ben je er dan al.
[...] onzin
[ Bericht 20% gewijzigd door t4rt4rus op 25-11-2014 20:02:39 ]
Ik begrijp niet wat je hier doet. Er hoeft helemaal geen punt X op lijn ℓ te liggen waarvan de afstand tot de oorsprong gelijk is aan 1 en ook hoeven de loodrechte projecties A' en B' van A en B op ℓ helemaal niet collineair te zijn met de oorsprong.quote:
Ik dacht je neemt de eenheidsvector c op de lijn L, dan is de projectie van a op L, a', gegeven door a' = (a.c)c.quote:
[..]
Ik begrijp niet wat je hier doet. Er hoeft helemaal geen punt X op lijn ℓ te liggen waarvan de afstand tot de oorsprong gelijk is aan 1 en ook hoeven de loodrechte projecties A' en B' van A en B op ℓ helemaal niet collineair te zijn met de oorsprong.
Is dit dan wat beter?
Waarin
Stel de lijn L gaat door de oorsprong.
Neem een vector c parallel aan lijn L.
Dan is de projectie van a op L geven door
En de projectie van b door
Waaruit volgt dat
[ Bericht 7% gewijzigd door t4rt4rus op 25-11-2014 22:03:46 ]
Bedankt voor je reactie, maar volgens mij gaat dit niet werken...quote:
[..]
Dit moet niet zo moeilijk zijn.
Schrijf a' en b' als a en b en c, gebruik de driehoeksongelijkheid en volgens mij ben je er dan al.
Je definieert nu c als een verzameling, hoe is dan het inproduct van a met c gedefinieerd?
Tevens, de verzameling c kan ook leeg zijn, je kunt namelijk jouw c opvatten als de doorsnede van de lijn L met de bol met straal 1. Die doorsnede kan leeg zijn.
Edit: Sorry, ik zie nu dat Riparius dit al had opgemerkt en je hier al op hebt gereageerd, even lezen.
Nogmaals edit:
Je beschouwt dus de eenheidsvector c die de richting van de lijn L bepaalt.
Kom je dan niet in de problemen zodra L niet door de oorsprong gaat?
Derde update:
Nogmaals bedankt voor je herziene uitwerking, echter ga je er mijns inziens nu (onterecht) vanuit dat
[ Bericht 5% gewijzigd door Hahatsjoe op 25-11-2014 20:09:09 ]
quote:
[..]
Bedankt voor je reactie, maar volgens mij gaat dit niet werken...
Je definieert nu c als een verzameling, hoe is dan het inproduct van a met c gedefinieerd?
Tevens, de verzameling c kan ook leeg zijn, je kunt namelijk jouw c opvatten als de doorsnede van de lijn L met de bol met straal 1. Die doorsnede kan leeg zijn.
Edit: Sorry, ik zie nu dat Riparius dit al had opgemerkt en je hier al op hebt gereageerd, even lezen.
Nogmaals edit:
Je beschouwt dus de eenheidsvector c die de richting van de lijn L bepaalt.
Kom je dan niet in de problemen zodra L niet door de oorsprong gaat?
Derde update:
Nogmaals bedankt voor je herziene uitwerking, echter ga je er mijns inziens nu (onterecht) vanuit dat. Waarom mag je dit zeggen?
Voor een scalar a geldt toch |x c| = |x| |c| ?
[ Bericht 4% gewijzigd door t4rt4rus op 25-11-2014 21:17:07 ]
Ja.quote:
[..]
Voor een scalar a geldt toch |a c| = |a| |c| ?
Ik snap alleen niet hoe je nu precies die c introduceert. Volgens mij bedoel je dat je de lijn als het ware parametriseerd.
Immers, elk punt op de lijn L kun je schrijven als
waarbij r de richtingsvector is en s de steunvector (en t is de parameter).
Definieer je nu
Ik ben gewoon (namen van) lijnen met kleine letters aan te geven en (namen van) punten met hoofdletters, dus dat zal ik hier ook doen. We hebben in R3 een rechte ℓ en tevens twee punten A en B waarvan we veronderstellen dat deze verschillend zijn. Laten verder A' en B' de loodrechte projecties zijn van resp. A en B op ℓ. Gevraagd wordt nu te bewijzen dat d(A', B') ≤ d(A, B).quote:
Als ik een rechte lijn
Intuïtief zou ik dan zeggen dat:
Klopt dit inderdaad? Zo ja, hoe zou ik dit kunnen bewijzen?
Moet ik de directe formule voor een projectie gebruiken, of is het simpelweg een kwestie van de driehoeksongelijkheid toepassen?
Ik zie het zo snel niet in, hulp zou gewaardeerd worden.
Als A' = B' dan is er niets meer te bewijzen, zodat we A' ≠ B' mogen veronderstellen. Laten we nu de vectoren OA, OB, OA', OB' aangeven met resp. a, b, a', b', dan is
ℓ: v = a' + λ(b' − a')
een vectorvoorstelling van de rechte ℓ. Liggen de punten A en B niet op ℓ, dan staan de lijnstukken AA' en BB' beide loodrecht op lijnstuk A'B', zodat
(1) (a' − a)·(b' − a') = 0
en
(2) (b' − b)·(b' − a') = 0
Merk op dat (1) en (2) eveneens gelden als de punten A en of B wel op ℓ liggen, aangezien a' − a resp. b' − b dan de nulvector is. Uit (1) en (2) volgt nu
(3) a'·(b' − a') = a·(b' − a')
en
(4) b'·(b' − a') = b·(b' − a')
en daarmee
(5) (b' − a')·(b' − a') = (b − a)·(b' − a')
zodat
(6) | b' − a' |2 = | b − a | · | b' − a' | · | cos ∠(b − a, b' − a') |
Maar nu is A' ≠ B' zodat | b' − a' | ≠ 0 en dus hebben we
(7) | b' − a' | = | b − a | · | cos ∠(b − a, b' − a') |
en daarmee
(8) | b' − a' | ≤ | b − a |
QED
[ Bericht 0% gewijzigd door Riparius op 27-11-2014 17:42:50 ]
Je bent zo te zien nog steeds in de war. Eerst was je a een vector, en nu is het weer een scalar. En het is onduidelijk wat je nu wil met die genormeerde richtingsvector van de rechte, die heb je helemaal niet nodig.quote:
[..]
Ja, zo ja.
Sorry was net even in de war.
Oh die laatste zin van mij had niet veel met de rest te maken.quote:
[..]
Je bent zo te zien nog steeds in de war. Eerst was je a een vector, en nu is het weer een scalar. En het is onduidelijk wat je nu wil met die genormeerde richtingsvector van de rechte, die heb je helemaal niet nodig.
In de rest is a gewoon een vector.
Maar het ging hier toch om een projectie van de vectoren a en b op de lijn L?
Nemen we een vector c parallel met de lijn L dan zijn de projecties gegeven door
x' = (x.ĉ)ĉ
Je kunt volgens mij die vraag makkelijk bewijzen in R^2 en dan veralgemeniseren naar R^3 en zo naar R^n.
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Nee, en dit is kennelijk je misverstand. Het gaat om de loodrechte projecties A' en B' van twee punten A resp. B op een rechte ℓ en om te bewijzen dat dan d(A', B') ≤ d(A, B).quote:
[..]
Oh die laatste zin van mij had niet veel met de rest te maken.
In de rest is a gewoon een vector.
Maar het ging hier toch om een projectie van de vectoren a en b op de lijn L?
Nemen we een vector c parallel met de lijn L dan zijn de projecties gegeven door
x' = (x.ĉ)ĉ
En laat ik dat in feite al hebben gedaan.quote:
Je kunt volgens mij die vraag makkelijk bewijzen in R^2 en dan veralgemeniseren naar R^3 en zo naar R^n.
Is dat niet gewoon hetzelfde als de projectie van de vectoren a en b op een vector c als we de lijn L door de oorsprong laten gaan?quote:
[..]
Nee, en dit is kennelijk je misverstand. Het gaat om de loodrechte projecties A' en B' van twee punten A resp. B op een rechte ℓ en om te bewijzen dat dan d(A', B') ≤ d(A, B).
De problemen zijn dan equivalent aan elkaar.
Het punt is dat de gegeven rechte ℓ niet door de oorsprong hoeft te gaan. Je lijkt ook niet te begrijpen dat de vier punten A, B, A' en B' niet in één vlak hoeven te liggen. Heb je mijn uitwerking bestudeerd en begrijp je deze ook?quote:
[..]
Is dat niet gewoon hetzelfde als de projectie van de vectoren a en b op een vector c als we de lijn L door de oorsprong laten gaan?
De problemen zijn dan equivalent aan elkaar.
Gelukkig maar.quote:
Ontzettend bedankt voor je uitwerking Riparius, het is volledig duidelijk!
Dan verander je de oorsprong zodat dat wel het geval is. Dat verandert toch niks aan het probleem?quote:
[..]
Het punt is dat de gegeven rechte ℓ niet door de oorsprong hoeft te gaan.
Waarom zou ik dat niet begrijpen?quote:Je lijkt ook niet te begrijpen dat de vier punten A, B, A' en B' niet in één vlak hoeven te liggen.
Nee nog niet.quote:Heb je mijn uitwerking bestudeerd en begrijp je deze ook?
Maar wat mankeert er aan mijn kladwerk?
-edit- Als ik aangeef dat we lijn L door de oorsprong laten gaan
-edit- Ik heb even heel snel naar jou uitwerking gekeken en snap wat je doet.quote:Stel de lijn L gaat door de oorsprong.
Neem een vector c parallel aan lijn L.
Dan is de projectie van a op L geven door
En de projectie van b door
Waaruit volgt dat
[ Bericht 9% gewijzigd door t4rt4rus op 25-11-2014 22:05:22 ]
De middelwaardestelling geldt in het algemeen niet voor (reguliere) krommen in R^n, toch? Ik kan namelijk zo wel enkele krommen bedenken in R^3 waarvoor deze stelling niet opgaat.
Ik zit echter in m'n maag met R^2, want ik kan hier geen juist tegenvoorbeeld voor bedenken. Ik krijg nu zelfs het vermoeden dat de stelling wel geldt in R^2.
Formeler gesproken, ik wil dus de volgende stelling bewijzen of ontkrachten:
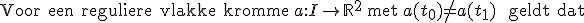
![\exists t \in [t_0, t_1] \ \text{zodanig dat} \ a'(t} \ \text{parallel is met de lijn} \ L \ \text{tussen} \ a(t_0) \ \text{en} \ a(t_1)](https://forum.fok.nl/lib/mimetex.cgi?%5Cexists%20t%20%5Cin%20%5Bt_0%2C%20t_1%5D%20%20%5C%20%5Ctext%7Bzodanig%20dat%7D%20%5C%20a%27%28t%7D%20%5C%20%5Ctext%7Bparallel%20is%20met%20de%20lijn%7D%20%5C%20L%20%5C%20%5Ctext%7Btussen%7D%20%5C%20a%28t_0%29%20%5C%20%5Ctext%7Ben%7D%20%5C%20a%28t_1%29%20)
.
Gaat het bewijs geheel analoog als het bewijs van de middelwaardestelling (uit de calculus)?
Ik zit echter in m'n maag met R^2, want ik kan hier geen juist tegenvoorbeeld voor bedenken. Ik krijg nu zelfs het vermoeden dat de stelling wel geldt in R^2.
Formeler gesproken, ik wil dus de volgende stelling bewijzen of ontkrachten:
Gaat het bewijs geheel analoog als het bewijs van de middelwaardestelling (uit de calculus)?
( 2log(p2-1) / 2log(4) ) - 2log(p+3) = (1/2)
2log(p2-1) - 2 * 2log(p+3) = 1
Kan iemand mij deze stap uitleggen? Ik kom er niet uit
2log(p2-1) - 2 * 2log(p+3) = 1
Kan iemand mij deze stap uitleggen? Ik kom er niet uit
Beide kanten zijn vermenigvuldigd met 2.quote:
( 2log(p2-1) / 2log(4) ) - 2log(p+3) = (1/2)
2log(p2-1) - 2 * 2log(p+3) = 1
Kan iemand mij deze stap uitleggen? Ik kom er niet uit
Merk op dat 2log (4) = 2 want 22 = 4.
Ik veronderstel dat je hier (x'(t), y'(t)) bedoelt met a'(t) als a(t) = (x(t), y(t)). De stelling die je wil bewijzen is in zijn algemeenheid niet waar. Wat je hier hebt is in feite de (gegeneraliseerde) middelwaardestelling van Cauchy die je wellicht bekend is omdat deze wordt gebruikt bij het bewijs van de regel van L'Hôpital.quote:
De middelwaardestelling geldt in het algemeen niet voor (reguliere) krommen in R^n, toch? Ik kan namelijk zo wel enkele krommen bedenken in R^3 waarvoor deze stelling niet opgaat.
Ik zit echter in m'n maag met R^2, want ik kan hier geen juist tegenvoorbeeld voor bedenken. Ik krijg nu zelfs het vermoeden dat de stelling wel geldt in R^2.
Formeler gesproken, ik wil dus de volgende stelling bewijzen of ontkrachten:.
Gaat het bewijs geheel analoog als het bewijs van de middelwaardestelling (uit de calculus)?
Betreffende je eerste zin, dat bedoel ik inderdaad. Ik had dat inderdaad voor de volledigheid op moeten merken.quote:
[..]
Ik veronderstel dat je hier (x'(t), y'(t)) bedoelt met a'(t) als a(t) = (x(t), y(t)). De stelling die je wil bewijzen is in zijn algemeenheid niet waar. Wat je hier hebt is in feite de (gegeneraliseerde) middelwaardestelling van Cauchy die je wellicht bekend is omdat deze wordt gebruikt bij het bewijs van de regel van L'Hôpital.
Ik kende deze stelling van Cauchy nog niet, bedankt voor het posten! Als ik het goed begrijp geldt de stelling dus wel voor R^2?
Nee, in de vorm waarin jij de stelling formuleert is deze niet algemeen geldig. In het Wikipedia artikel wordt een tegenvoorbeeld gegeven. De curve met als parametervoorstellingquote:
[..]
Betreffende je eerste zin, dat bedoel ik inderdaad. Ik had dat inderdaad voor de volledigheid op moeten merken.
Ik kende deze stelling van Cauchy nog niet, bedankt voor het posten! Als ik het goed begrijp geldt de stelling dus wel voor R^2?
x(t) = t3
y(t) = 1 − t2
waarbij we t het interval [−1, 1] laten doorlopen heeft als beginpunt (−1, 0) en als eindpunt (1, 0) maar deze curve heeft nergens een horizontale raaklijn. Check.
Bedankt voor je reactie.quote:
[..]
Nee, in de vorm waarin jij de stelling formuleert is deze niet algemeen geldig. In het Wikipedia artikel wordt een tegenvoorbeeld gegeven. De curve met als parametervoorstelling
x(t) = t3
y(t) = 1 − t2
waarbij we t het interval [−1, 1] laten doorlopen heeft als beginpunt (−1, 0) en als eindpunt (1, 0) maar deze curve heeft nergens een horizontale raaklijn. Check.
Echter, met de eis dat het een reguliere curve is, dus
Ah ja, inderdaad, dat had ik over het hoofd gezien in je formulering. In bovenstaande parametervoorstelling zijn x'(t) en y'(t) beide 0 voor t = 0.quote:
[..]
Bedankt voor je reactie.
Echter, met de eis dat het een reguliere curve is, dus, klopt het toch wel?
Beetje laat, maar hier alsnog een reply. In het minimale punt van de LAC (Long-term average costs) snijdt de MC-lijn met de LAC. Dus daardoor weet je dat de marginale kosten van labour en capital gelijk zijn in dat punt.quote:
Ik kom niet uit een opgave over short-run marginal costs and minimum costs in the long run en ik hoop meer duidelijkheid hier te verschaffen:
De opgave:
A firm with the production function Q = F(K, L) is producing an output level of Q* at minimum costs in the long run. How will its short-run marginal cost when K is fixed compare with its short-run marginal cost when L is fixed?
Antwoord:
At the minimum-cost input bundle for producing Q*, we know that the extra output obtained
from the last dollar spent on labor is the same as the extra output obtained from the last dollar spent on capital. Thus the two short-run marginal cost curves will take the same value at Q*.
Ik snap het antwoord niet.. Hoe kunnen de twee short-run marginal costs dezelfde waarde geven op Q, ondanks dat ze verschillen (de 1 waar K vast is en de ander waar L vast is ) ?
Ik snap de gedachte/visualisatie er niet van.. Daarnaast snap ik niet wat het vetgedrukte met de vraag te maken heeft? Ik snap de regel wel, maar ik snap niet wat voor invloed het heeft op de twee short-run curves.. waardoor ze op 1 of andere manier toch dezelfde Q* geven..
Alvast bedankt.
Goedemorgen allen,
Ik heb een vraag over de afgeleide van een functie waar ik niet bekend mee ben en ik hoop dat iemand mij uit de brand kan helpen.
:
F(K,L) = min(aK,bL)
De afgeleiden die ik moet berekenen zijn: d F(K,L)/ d K en d F(K,L)/ d L
Alvast bedankt.
Ik heb een vraag over de afgeleide van een functie waar ik niet bekend mee ben en ik hoop dat iemand mij uit de brand kan helpen.
:F(K,L) = min(aK,bL)
De afgeleiden die ik moet berekenen zijn: d F(K,L)/ d K en d F(K,L)/ d L
Alvast bedankt.
quote:
Goedemorgen allen,
Ik heb een vraag over de afgeleide van een functie waar ik niet bekend mee ben en ik hoop dat iemand mij uit de brand kan helpen.
F(K,L) = min(aK,bL)
De afgeleiden die ik moet berekenen zijn: d F(K,L)/ d K en d F(K,L)/ d L
Alvast bedankt.
Probeer dat te gebruiken. Dan hoef je alleen nog maar op te letten waar de functie niet differentieerbaar is.
Oke hartstikke bedankt!quote:
[..]
Probeer dat te gebruiken. Dan hoef je alleen nog maar op te letten waar de functie niet differentieerbaar is.
Nog een vraag:
Wat is de afgeleide naar K en L (dQ/dK en dQ/dL) van de volgende functie?:
Ik had het allereerst herschreven tot:
2L * k1/2 * L 1/2
Dus:
2L3/2 * k1/2
dQ/dK = L3/2 * K -1/2
dQ/dL = 3L1/2 * K 1/2
Het antwoordenboek zegt echter wat anders:
Jij hebt het goed. Het antwoordenboek is in dit geval fout.quote:
[..]
Het antwoordenboek zegt echter wat anders:
[ afbeelding ]
quote:
[..]
Jij hebt het goed. Het antwoordenboek is in dit geval fout.
Deze antwoorden kloppen dus niet?
Ik vraag het maar voor de zekerheid, want ik begon, na een uur bezig te zijn, aan mijzelf te twijfelen of ik nou niet fout bezig was..
Ik kom niet uit een bewijsopgave.
Zij V ⊂ R^5 de deelruimte die gegeven wordt door de vergelijking x1+x2+x3−x4−x5 = 0.
Bewijs dat V een lineaire deelruimte is, bepaal de dimensie van V en bepaal een
basis (toon ook aan dat dit inderdaad een basis is).
welke assumpties heb ik nodig om dit bewijs te kunnen leveren? Het begrip lineaire deelruimte is nog redelijk abstract voor mij en uit de literatuur die ik heb kan ik ook niet veel opmaken. Iemand die mij op weg kan helpen?
Zij V ⊂ R^5 de deelruimte die gegeven wordt door de vergelijking x1+x2+x3−x4−x5 = 0.
Bewijs dat V een lineaire deelruimte is, bepaal de dimensie van V en bepaal een
basis (toon ook aan dat dit inderdaad een basis is).
welke assumpties heb ik nodig om dit bewijs te kunnen leveren? Het begrip lineaire deelruimte is nog redelijk abstract voor mij en uit de literatuur die ik heb kan ik ook niet veel opmaken. Iemand die mij op weg kan helpen?
Heb je uberhaupt iets geprobeerd?quote:
Ik kom niet uit een bewijsopgave.
Zij V ⊂ R^5 de deelruimte die gegeven wordt door de vergelijking x1+x2+x3−x4−x5 = 0.
Bewijs dat V een lineaire deelruimte is, bepaal de dimensie van V en bepaal een
basis (toon ook aan dat dit inderdaad een basis is).
welke assumpties heb ik nodig om dit bewijs te kunnen leveren? Het begrip lineaire deelruimte is nog redelijk abstract voor mij en uit de literatuur die ik heb kan ik ook niet veel opmaken. Iemand die mij op weg kan helpen?
De opgave zegt dat je moet bewijzen dat een deelruimte lineair is. Wanneer een ruimte lineair is, zou in je dictaat/boek moeten staan, maar als je het even niet kan vinden kan je het ook prima googelen. Er is gewoon een rij definities waar een ruimte aan moet voldoen om lineair te zijn. Je weet als het goed is dat R5 (of, algemener, Rn, voor elk natuurlijk getal n) een vectorruimte (wat een ander woord is voor een lineaire ruimte) is, dat helpt bij veel voorwaarden die je moet bewijzen.
Kijk maar even hoe ver je nu komt. Mocht je er nog niet uitkomen, help ik je graag verder als je wat duidelijker probeert aan te geven wat je probleem is.
[ Bericht 7% gewijzigd door defineaz op 30-11-2014 17:22:13 ]
Ik moet een bewijs presenteren, waarbij het resultaat van de volgende oefening wordt gebruikt. Ik kom er niet uit:
q is overigens groter of gelijk aan 1.
Ik heb geprobeerd de integraal over Rn op verschillende manieren om te schrijven. De meest veelbelovende manier leek me om de integraal over Rn als een integraal over een bol te schrijven, en het limiet te nemen als de straal van de bol naar oneindig gaat. In dit geval moet je ofwel een dubbele limiet nemen, of een straal nemen die afhangt van h.
Het lijkt me intuitief een goed idee om de bol B(h/2, |h|) te nemen en deze bol te splitsen in de bollen
A := B(0, |h|/2)
B := B(h, |h|/2)
en de rest
C := B(h/2, |h|) \ (A U B)
Volgens mij zou de integraal over C naar 0 moeten gaan als |h| naar oneindig gaat.
Je kan nu zeggen dat |x| en |x + h| allebei groter zijn dan |h|/2 in de integraal over C (anders zit x namelijk in A of B). Het lukt me alleen niet om hier nuttige afschattingen mee te maken (wat weer te maken heeft met de macht q in de integraal.
Enige tips zijn welkom! De opgave is 2.5.1 uit 'Classical Fourier Analysis' van Lukas Grafakos (lichtelijk omgeschreven).
q is overigens groter of gelijk aan 1.
Ik heb geprobeerd de integraal over Rn op verschillende manieren om te schrijven. De meest veelbelovende manier leek me om de integraal over Rn als een integraal over een bol te schrijven, en het limiet te nemen als de straal van de bol naar oneindig gaat. In dit geval moet je ofwel een dubbele limiet nemen, of een straal nemen die afhangt van h.
Het lijkt me intuitief een goed idee om de bol B(h/2, |h|) te nemen en deze bol te splitsen in de bollen
A := B(0, |h|/2)
B := B(h, |h|/2)
en de rest
C := B(h/2, |h|) \ (A U B)
Volgens mij zou de integraal over C naar 0 moeten gaan als |h| naar oneindig gaat.
Je kan nu zeggen dat |x| en |x + h| allebei groter zijn dan |h|/2 in de integraal over C (anders zit x namelijk in A of B). Het lukt me alleen niet om hier nuttige afschattingen mee te maken (wat weer te maken heeft met de macht q in de integraal.
Enige tips zijn welkom! De opgave is 2.5.1 uit 'Classical Fourier Analysis' van Lukas Grafakos (lichtelijk omgeschreven).
ah zie het nu. Dat zijn dus deze eigenschappen:quote:
[..]
Heb je uberhaupt iets geprobeerd?
De opgave zegt dat je moet bewijzen dat een deelruimte lineair is. Wanneer een ruimte lineair is, zou in je dictaat/boek moeten staan, maar als je het even niet kan vinden kan je het ook prima googelen. Er is gewoon een rij definities waar een ruimte aan moet voldoen om lineair te zijn. Je weet als het goed is dat R5 (of, algemener, Rn, voor elk natuurlijk getal n) een vectorruimte (wat een ander woord is voor een lineaire ruimte) is, dat helpt bij veel voorwaarden die je moet bewijzen.
Kijk maar even hoe ver je nu komt. Mocht je er nog niet uitkomen, help ik je graag verder als je wat duidelijker probeert aan te geven wat je probleem is.
1. Als x ∈ W en y ∈ W, dan geldt x + y ∈ W
2. Als x ∈ W en λ ∈ R, dan geldt λx ∈ W.
3. De nulvector 0 is bevat in W.
alleen hoe is dit toe te passen op de opgave? De derde stelling is simpel, maar wat wordt precies bedoeld met de eerste en tweede stelling?
Zij x = (x1, x2, x3, x4, x5) ∈ W en y = (y1, y2, y3, y4, y5) ∈ W. Dan x1+x2+x3−x4−x5 = 0 en y1+y2+y3−y4−y5 = 0.quote:
alleen hoe is dit toe te passen op de opgave? De derde stelling is simpel, maar wat wordt precies bedoeld met de eerste en tweede stelling?
Uit die twee vergelijkingen volgt x1+x2+x3−x4−x5 + y1+y2+y3−y4−y5 = (x1+y1)+(x2+y2)+(x3+y3)−(x4+y4)−(x5+y5) = 0.
Nu jij weer.
Ik zie één vergelijking met twee onbekenden. Jij ook?quote:
9 - Q2/2 = 9 - Q1/2
Hoe los je dit op? Q2 = productie van bedrijf 2 en Q1 = productie van bedrijf 1.
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Opinion is the medium between knowledge and ignorance (Plato)
quote:
[..]
Ik zie één vergelijking met twee onbekenden. Jij ook?Q2 = Q - Q1SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
Q1 = Q - Q2
Waar Q = Total Quantity..
Bedoel je dit?
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |