[Bèta wiskunde] Huiswerk- en vragentopic.

quote:

Op zondag 12 oktober 2014 22:33 schreef Janneke141 het volgende:

[..]

Heb je ooit uitleg gehad over de achtergrond van differentiëren, met limieten en dergelijke?

Ja tot op zekere hoogte. Ik weet van de volgende onderwerpen af:

-Differentiëren (constante, som-, product-, quotiëntregel)

-Limieten berekenen

-L'hopital

Wat betreft de achtergrond: ik heb wel bepaalde theorie waar ik dus nog niet alles van begrijp zoals de differentieerbaarheid, newton quotient en de afgeleiden berekenen met de standaard rate of change formule i.p.v. standaardregels.


Omdat de achtergrond van het differentieren er niet goed in zit bij mij, stel ik mijzelf veel waarom vragen en dan stel ik mij de vragen, zoals gesteld op de vorige pagina.

quote:

Op zondag 12 oktober 2014 22:31 schreef GoldenHeart het volgende:
Hallo wiskundigen,
Ik zat te denken over differentieerbaarheid en ik vroeg mij dus het volgende af:
-Waarom is | x | niet differentieerbaar in het punt x= 0? Ik weet dat er op dat punt een knik is, echter vraag ik mij af hoe dit te berekenen is, evenals hoe je kunt berekenen of | x | differentieerbaar is in het punt x=2.
Kort samengevat: hoe kun je de differentieerbaarheid in bepaalde punten berekenen?

Differentieerbaarheid bereken je niet maar toon je aan. Begin maar eens met deze post van mij goed door te nemen.

quote:

Op zondag 12 oktober 2014 22:39 schreef Riparius het volgende:

[..]

Differentieerbaarheid bereken je niet maar toon je aan. Begin maar eens met deze post van mij goed door te nemen.

Ik had mij even beperkt tot het stuk m.b.t. differentieerbaarheid en daar impliceer je dat de differentieerbaarheid te berekenen is d.m.v. de definitie van de afgeleide. Echter vraag ik mij af of er ook dit aan te tonen is d.m.v. een tweede methode; zoals het direct te bepalen van de afgeleide (d.m.v. de regels) en verbolgens dan wat met het punt (laten we stellen) x = 2 moeten doen (zoals invullen in f(x) of f'(x) ).

quote:

Op zondag 12 oktober 2014 22:47 schreef GoldenHeart het volgende:
[..]
Ik had mij even beperkt tot het stuk m.b.t. differentieerbaarheid en daar impliceer je dat de differentieerbaarheid te berekenen is d.m.v. de definitie van de afgeleide. Echter vraag ik mij af of er ook dit aan te tonen is d.m.v. een tweede methode; zoals het direct te bepalen van de afgeleide (d.m.v. de regels) en verbolgens dan wat met het punt (laten we stellen) x = 2 moeten doen (zoals invullen in f(x) of f'(x) ).

Differentieerbaarheid is een eigenschap, en eigenschappen toon je aan. Het hellingsgetal op een bepaalde plek is een getal, en die kan je berekenen.
Wat je weet van differentieerbaarheid zijn een aantal rekenregels voor het differentiëren van bepaalde functies. Afhankelijk van wat je precies moet kunnen zou je daar nog wel een heel eind mee kunnen komen, maar voor je kennis van het begrip 'differentieerbaarheid', en ook hoe die rekenregels nou precies tot stand zijn gekomen, is meer achtergrondkennis nodig. Zie de link van Riparius. Die kennis heb je eigenlijk wel nodig om op een nette manier differentieerbaarheid te kunnen aantonen.

Blijft het bij huis-, tuin- en keukenfuncties, zoals f(x) = |x|, dan kun je met wat rekenregels nog wel een eind komen.
Omdat f(x) = x voor x>0 en f(x) = -x voor x<0, kun je met de jou bekende rekenregels makkelijk zien dat f'(x) = 1 (voor x>0) en f'(x) = -1 (voor x<0).
Wil een functie f in een bepaald punt a differentieerbaar zijn, dan zal lim_{x →a}f'(x) moeten bestaan. Voor x=2 is dit wel duidelijk.
Voor x=0 is vrij makkelijk te zien dat f daar niet differentieerbaar is, omdat
lim_{x ↓0}f'(x) = 1, en lim_{x ↑0}f'(x) = -1

quote:

Op zondag 12 oktober 2014 22:57 schreef Janneke141 het volgende:
[..]

Wil een functie f in een bepaald punt a differentieerbaar zijn, dan zal lim_{x →a}f'(x) moeten bestaan.

Nee Janneke, dit is niet waar. Kijk hier maar eens.

quote:

Op zondag 12 oktober 2014 23:08 schreef Riparius het volgende:
[..]
Nee Janneke, dit is niet waar. Kijk hier maar eens.

Wel voor huis-, tuin- en keukenfuncties

Maar je hebt (uiteraard) gelijk.

quote:

Op zondag 12 oktober 2014 22:47 schreef GoldenHeart het volgende:
[..]
Ik had mij even beperkt tot het stuk m.b.t. differentieerbaarheid en daar impliceer je dat de differentieerbaarheid te berekenen is d.m.v. de definitie van de afgeleide. Echter vraag ik mij af of er ook dit aan te tonen is d.m.v. een tweede methode; zoals het direct te bepalen van de afgeleide (d.m.v. de regels) en vervolgens dan wat met het punt (laten we stellen) x = 2 moeten doen (zoals invullen in f(x) of f'(x) ).

Nee, want dan maak je je schuldig aan een petitio principii. Dat wil zeggen dat je datgene wat je wil bewijzen al op voorhand voor waar aanneemt, en dan bewijs je niets. Die regels die jij wil toepassen gelden namelijk voor differentieerbare functies, dus als je op die regels steunt, dan neem je impliciet al differentieerbaarheid aan en is je 'bewijs' dus sowieso ongeldig.

Ik lees soms door deze reeks omdat ik het wel kan waarderen dat wiskunde een soort apart taaltje is, waardoor ik een Nederlandse tekst kan lezen en toch geen flauw idee heb waar het over gaat

+ omdat het cool is dat hier mensen zitten die anderen écht helpen iets te begrijpen

Hey, daar ben ik weer en ik heb weer eens wat vragen. Ditmaal over partiële afgeleiden. Ik hoop dat iemand mij uit de brand kan helpen:

Ik zou de partiële elasticiteit van z = xⁿe^xyⁿe^y moeten vinden voor z with respect to x ( d z / d x).

Hierbij heb ik de volgende elasticiteitsformule gebruikt: (x / z) * (d z / d x)

( x / xⁿe^xyⁿe^y ) * nx^n-1e^xyⁿe^y

Dit maakt:

x * ( nx^n-1e^xyⁿe^y ) / xⁿe^xyⁿe^y

de -1 exponent eruit halen door x ^-1 buiten de haakjes te halen, evenals de n, zodat zowel de noemer als teller gedeeld kunnen worden door één dezelfde term:


x * x ^-1 * n ( x^n-1e^xyⁿe^y ) / xⁿe^xyⁿe^y


Het antwoord wordt dus gewoon = n

Echter moet het x + n zijn...


Tenslotte:


''let z = x1^p ...... xn^p exp(a1x1 + ...... + an xn) , where a1, ..... , an, and p are constants. Find the partial elasticities of z w.r.t. x1, ...... , xn.''

Hoe moet ik dit doen? Ik ben het recht toe recht aan gewend en niet met de sommatie notatie.

[ Bericht 4% gewijzigd door Super-B op 13-10-2014 19:29:03 ]

quote:

Op maandag 13 oktober 2014 19:18 schreef Super-B het volgende:
Hey, daar ben ik weer en ik heb weer eens wat vragen. Ditmaal over partiële afgeleiden. Ik hoop dat iemand mij uit de brand kan helpen:
Ik zou de partiële elasticiteit van z = xⁿe^xyⁿe^y moeten vinden voor z with respect to x ( d z / d x).
Hierbij heb ik de volgende elasticiteitsformule gebruikt: (x / z) * (d z / d x)
( x / xⁿe^xyⁿe^y ) * nx^n-1e^xyⁿe^y
Dit maakt:
x * ( nx^n-1e^xyⁿe^y ) / xⁿe^xyⁿe^y
de -1 exponent eruit halen door x ^-1 buiten de haakjes te halen, evenals de n, zodat zowel de noemer als teller gedeeld kunnen worden door één dezelfde term:
x * x ^-1 * n ( x^n-1e^xyⁿe^y ) / xⁿe^xyⁿe^y
Het antwoord wordt dus gewoon = n
Echter moet het x + n zijn...

Je moet de productregel gebruiken, dz/dx ≠ nx^n-1e^xyⁿe^y.

quote:

Op maandag 13 oktober 2014 19:33 schreef zerak het volgende:
[..]
Je moet de productregel gebruiken, dz/dx ≠ nx^n-1e^xyⁿe^y.

Dat komt vanwege de e^x neem ik aan? Hoe moet ik bovendien de overige constante zien (y^n en e^y)? Moet ik die even wegdenken of..?

quote:

Op maandag 13 oktober 2014 19:39 schreef Super-B het volgende:
[..]
Dat komt vanwege de e^x neem ik aan? Hoe moet ik bovendien de overige constante zien (y^n en e^y)? Moet ik die even wegdenken of..?

Inderdaad. yⁿe^y behandel je gewoon als elke andere constante.
Je krijgt hier dz/dx = nx^n-1e^xyⁿe^y + xⁿe^xyⁿe^y.

Schrijf . Dan heb je

quote:

Op maandag 13 oktober 2014 19:41 schreef zerak het volgende:
[..]
Inderdaad. yⁿe^y behandel je gewoon als elke andere constante.
Je krijgt hier dz/dx = nx^n-1e^xyⁿe^y + xⁿe^xyⁿe^y.

quote:

Op maandag 13 oktober 2014 19:49 schreef Novermars het volgende:
Schrijf . Dan heb je

Top, bedankt!

quote:

Op maandag 13 oktober 2014 19:18 schreef Super-B het volgende:
Tenslotte:
''let z = x1^p ...... xn^p exp(a1x1 + ...... + an xn) , where a1, ..... , an, and p are constants. Find the partial elasticities of z w.r.t. x1, ...... , xn.''
Hoe moet ik dit doen? Ik ben het recht toe recht aan gewend en niet met de sommatie notatie.

Je hebt dus z(x_i) = x_i^pe^ai·xi voor i ∈ {1, ...., n}.
z'(x_i) = px_i^p-1e^ai·xi + a_ix_i^pe^ai·xi.

El_zi = x/z(x_i) * z'(x_i) = ((p + a_ix_i) x_i^pe^ai·xi) / (x_i^pe^ai·xi) = p + a_ix_i.

[ Bericht 0% gewijzigd door zerak op 13-10-2014 20:49:45 ]

Hoi, zou iemand mij met een kleine onduidelijkheid kunnen helpen?

Het vraagstuk dat ik moet oplossen is als volgt:

Find dz / dt for the following cases:

z =(x - y) / (x + y), x = e^{t +s} , y = e^ts

Ik heb het antwoord opgezocht in een antwoordenmodel op het internet en het antwoord luidt:



Ik heb exact hetzelfde antwoord op één iets na en dat is dat ik in het rechterdeel op -2x uitkom i.p.v -2sx..

Omdat ik het oplos met de quotientregel, was mijn methode voor het rechterdeel als volgt:

quote:

Op dinsdag 14 oktober 2014 11:26 schreef GoldenHeart het volgende:
Find dz / dt for the following cases:

Kettingregel. Wat is de afgeleide van exp(ts) naar t?

quote:

Op dinsdag 14 oktober 2014 11:28 schreef Novermars het volgende:
[..]
Kettingregel. Wat is de afgeleide van exp(ts) naar t?

s, ow.. ik heb hem al door... Dankjewel voor de wake-up call.

Weer een vraag vanuit mijn kant:

If u = ln (x³ + y³ + z³ - 3xyz ), show that:

( i ) x * du/dx + y * du/dy + z * du/dz = 3

&

(ii) (x + y + z) (du/dx + du/dy + du/dz) = 3

( i ) Ik kom toch echt uit op: 3 + 3 + 3 = 9 i.p.v 3. Want als ik x * du/dx bereken, dan kom ik uit op 3 want ik krijg de mogelijkheid (na het berekenen van de afgeleide en het vermenigvuldigen van x) om zowel de teller als de noemer te delen door wat er in de noemer staat..zodat er alleen 3 overblijft, en dit geldt dan ook voor y * du/dy en z * du/dz

(ii) ik heb de afgeleiden berekend, maar hoe kan ik bewijzen dat het gelijk is aan 3 uiteindelijk? Want ik weet niet hoe ik dat kan laten zien met nog de vermenigvuldigen met (x + y + z) ernaast.. Ik 'zie het' niet zeg maar.

Laat je werk maar zien. Wolfram|alpha geeft een verschrikkelijke afgeleide en ik heb geen zin om alles uit te werken.

quote:

Op dinsdag 14 oktober 2014 13:20 schreef Novermars het volgende:
Laat je werk maar zien. Wolfram|alpha geeft een verschrikkelijke afgeleide en ik heb geen zin om alles uit te werken.

quote:

Op dinsdag 14 oktober 2014 13:24 schreef GoldenHeart het volgende:
[..]
[ afbeelding ]
[ afbeelding ]

Prachtig toch? Als je dat nog even optelt krijg je 3v/v = 3.

quote:

Op dinsdag 14 oktober 2014 13:38 schreef Riparius het volgende:
[..]
Prachtig toch? Als je dat nog even optelt krijg je 3v/v = 3.

Ow top!

Nog een vraagstuk:

Find y'' for y⁵ - x⁶ = 0

Eerst ging ik op zoek naar y'

5y⁴ * y' - 6x⁵ = 0

y' = 6x⁵ / 5y⁴ = 0

Nu y'' berekenen:

20y³ * y' * y' + 5y⁴ * y'' - 30x⁴ = 0

y' invullen voor bovenstaande levert:

(120x⁵y³ / 5y⁴) *( 6x⁵ / 5y⁴) + 5y⁴ * y'' - 30x⁴ = 0

(720x¹⁰y³ / 25y⁸ )+ 5y⁴ * y'' = 30x⁴

Breuk delen door 5:

(144x¹⁰ / 5y⁵) + 5y⁴ * y'' = 30x⁴

y'' = (6x⁴ / y⁴ ) - (144x¹⁰ / 5y⁵)

Doe ik het goed?

[ Bericht 0% gewijzigd door GoldenHeart op 14-10-2014 15:21:12 ]

quote:

Op dinsdag 14 oktober 2014 13:58 schreef GoldenHeart het volgende:
[..]
Ow top!
Nog een vraagstuk:
Find y'' for y⁵ - x⁶
Eerst ging ik op zoek naar y'
5y⁴ * y' - 6x⁵
y' = 6x⁵ / 5y⁴

STOP. Waar komt dat =-teken opeens vandaan?

Kijk nog eens goed naar de precieze formulering van het vraagstuk. Je lijdt aan dezelfde kwaal als veel anderen hier de laatste tijd, namelijk het negeren van =-tekens en hetgeen rechts daarvan staat om het =-teken dan als het je zo uitkomt plotseling weer op te laten duiken. Maar dat is geen geldige herleiding. Zoals jij de vraag weergeeft is die niet te beantwoorden.

quote:

Doe ik het goed?

Nee.

quote:

Op dinsdag 14 oktober 2014 14:09 schreef Riparius het volgende:
[..]
STOP. Waar komt dat =-teken opeens vandaan?
Kijk nog eens goed naar de precieze formulering van het vraagstuk. Je lijdt aan dezelfde kwaal als veel anderen hier de laatste tijd, namelijk het negeren van =-tekens en hetgeen rechts daarvan staat om het =-teken dan als het je zo uitkomt plotseling weer op te laten duiken. Maar dat is geen geldige herleiding. Zoals jij de vraag weergeeft is die niet te beantwoorden.
[..]
Nee.

Zie edit.

quote:

Op dinsdag 14 oktober 2014 13:58 schreef GoldenHeart het volgende:
[..]
Ow top!
Nog een vraagstuk:
Find y'' for y⁵ - x⁶ = 0
Eerst ging ik op zoek naar y'
5y⁴ * y' - 6x⁵ = 0
y' = 6x⁵ / 5y⁴ = 0
Nu y'' berekenen:

Nee, dit is weer fout opgeschreven. Hier beweer je namelijk dat y' = 0, maar dan hoef je niets meer te berekenen, want dan is ook y'' = 0.

quote:

Op dinsdag 14 oktober 2014 14:21 schreef Riparius het volgende:
[..]
Nee, dit is weer fout opgeschreven. Hier beweer je namelijk dat y' = 0, maar dan hoef je niets meer te berekenen, want dan is ook y'' = 0.
Je hoeft trouwens y' helemaal niet vrij te maken voordat je opnieuw (impliciet) gaat differentiëren, had je dat al bedacht?

Daar ben ik mij bewust van.

Ik maak y' alleen vrij om het later weer in te vullen..

quote:

Op dinsdag 14 oktober 2014 14:23 schreef GoldenHeart het volgende:
[..]
Daar ben ik mij bewust van.
Ik maak y' alleen vrij om het later weer in te vullen..

Ja, ik zag het nu.

quote:

Op dinsdag 14 oktober 2014 13:58 schreef GoldenHeart het volgende:
[..]

Doe ik het goed?

Nee, het klopt nog steeds niet. Je maakt op het laatst een fout. Verder is het overzichtelijker om eerst een uitdrukking voor y'' op te schrijven en dan pas de gevonden uitdrukking voor y' te substitueren.

quote:

Op dinsdag 14 oktober 2014 14:42 schreef Riparius het volgende:
[..]
Nee, het klopt nog steeds niet. Je maakt op het laatst een fout. Verder is het overzichtelijker om eerst een uitdrukking voor y'' op te schrijven en dan pas de gevonden uitdrukking voor y' te substitueren.

Kun je quoten waar ik de fout bega??

quote:

Op dinsdag 14 oktober 2014 14:45 schreef GoldenHeart het volgende:
[..]
Kun je quoten waar ik de fout bega??

Overgang naar de laatste regel. Daar ga je te snel en daarmee ook de fout in.

quote:

Op dinsdag 14 oktober 2014 14:51 schreef Riparius het volgende:
[..]
Overgang naar de laatste regel. Daar ga je te snel en daarmee ook de fout in.

Ik heb het niet door hahah.

quote:

Op dinsdag 14 oktober 2014 14:51 schreef Riparius het volgende:
[..]
Overgang naar de laatste regel. Daar ga je te snel en daarmee ook de fout in.

quote:

Op dinsdag 14 oktober 2014 14:56 schreef GoldenHeart het volgende:
[..]
Ik heb het niet door hahah.

Wat zou ik precies fout gedaan moeten hebben? Ik zit er al enige tijd naar te zoeken, maar ik kan de fout niet vinden (althans tot nu toe).

quote:

Op dinsdag 14 oktober 2014 15:12 schreef GoldenHeart het volgende:
[..]
[..]
Wat zou ik precies fout gedaan moeten hebben? Ik zit er al enige tijd naar te zoeken, maar ik kan de fout niet vinden (althans tot nu toe).

Je vergeet in de tweede term door 5y^4 te delen

quote:

Op dinsdag 14 oktober 2014 15:17 schreef Alrac4 het volgende:
[..]
Je vergeet in de tweede term door 5y^4 te delen

Ja maar het klopt wel? Ik keek even in het antwoordenmodel en het blijkt dat ik 5y⁹ moet hebben i.p.v. 5y⁴. Echter zie ik niet bij welk stuk ik op 5y^9 moest komen..

quote:

Op dinsdag 14 oktober 2014 15:20 schreef GoldenHeart het volgende:
[..]
Ja maar het klopt wel? Ik keek even in het antwoordenmodel en het blijkt dat ik 5y⁹ moet hebben i.p.v. 5y⁴. Echter zie ik niet bij welk stuk ik op 5y^9 moest komen..

Volgens mij klopt het tot aan de voorlaatste regel.
Je hebt:



Om y" te elimineren moet je de eerste term naar de rechterkant halen en dan alles delen door 5y^4.
De eerste term in je uitdrukking voor y" (de laatste regel) klopt. Bij de tweede term vergeet je echter te delen door 5y^4:

quote:

Op dinsdag 14 oktober 2014 15:37 schreef Alrac4 het volgende:
[..]
Volgens mij klopt het tot aan de voorlaatste regel.
Je hebt:

Om y" te elimineren moet je de eerste term naar de rechterkant halen en dan alles delen door 5y^4.
De eerste term in je uitdrukking voor y" (de laatste regel) klopt. Bij de tweede term vergeet je echter te delen door 5y^4:

Jeetje.. Een detail dat ik overzag, maar wel een cruciale fout. Dank voor je tijd.

Hey,

Ik heb een vraag met betrekking tot de homogeniteit van een functie. Het gaat om deze functie:

F( K, L ) = A[aK^-e + bL^-e) ^-1/e

Dit is de vraagstelling:'' Prove the CES function F (K, L ) is homogenous of degree one. Express F(K,L) / L as a function of k = K / L''

Ik begon met de bewijslast van de homogeniteit van graad 1:

F( tK, tL) = A[a * t^-e * K^-e + b * t ^-e * L^-e) ^-1/e

(t^-e ) ^{-1/ e} F(K , L )

t * F(K , L )

Is dit een goed antwoord of niet? De antwoorden achterin mijn boek is wat kort door de bocht om het te controleren. Daarnaast vraag ik mij af hoe ik het laatste stuk van de opgave kan maken: ''Express F(K,L) / L as a function of k = K / L''

Ik snap de bedoeling van dit laatste niet eens.. laat staan het maken ervan.

Hoi goedenavond,

Zou iemand mij iets kunnen vertellen over de Lagrange functie (waaronder de eerste en de voldoende voorwaarden) en de geometrische interpretatie hiervan? Ik vind het zelf een vrij lastig onderwerp, met name omdat ik niet echt snap waarvoor het dient, want je kunt toch al een maximum/minimum berekenen d.m.v. partieel afgeleiden, waarom zou je de Lagrange functie nodig moeten hebben..? Op internet tref ik veel literatuur wat er al vanuit gaat dat je al een redelijke kennis over het onderwerp beschikt, wat het voor mij lastig maakt.

quote:

Op dinsdag 14 oktober 2014 21:34 schreef RustCohle het volgende:
Hoi goedenavond,
Zou iemand mij iets kunnen vertellen over de Lagrange functie (waaronder de eerste en de voldoende voorwaarden) en de geometrische interpretatie hiervan?

Heb je je boek gelezen?

Staat daar niks in over Lagrange multipliers?

Simpel voorbeeld waarom partiële afgeleides niet nuttig zijn: Stel je hebt de functie gedefinieerd door f(x)=x^2 op het domein A=[2,4]. en je wilt 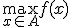bepalen. Hoe ga je dit doen met partiële afgeleides?

Voor wat extra literatuur. In Simon & Blume's Mathematics for Economists staat heel erg veel beschreven over dit soort problemen.

quote:

Op dinsdag 14 oktober 2014 22:02 schreef t4rt4rus het volgende:
[..]
Heb je je boek gelezen?
Staat daar niks in over Lagrange multipliers?

Jawel, maar er wordt het niet fatsoenlijk uitgelegd.

quote:

Op dinsdag 14 oktober 2014 22:09 schreef Novermars het volgende:
Simpel voorbeeld waarom partiële afgeleides niet nuttig zijn: Stel je hebt de functie gedefinieerd door f(x)=x^2 op het domein A=[2,4]. en je wilt bepalen. Hoe ga je dit doen met partiële afgeleides?
Voor wat extra literatuur. In Simon & Blume's Mathematics for Economists staat heel erg veel beschreven over dit soort problemen.

Het stationaire punt bepalen door f'(x) te bepalen en vervolgens te kijken wanneer f'(x) = 0 en dan een getallenlijn maken voor de getallen van het domein om zodoende het hoogste punt te bepalen.., het zijn overigens maar 3 getallen.. In dit geval is het maximum bij x= 4 want y= 16 dan. (?)

Misschien spreek ik mijzelf weer tegen, want het stationaire punt is bij x = 0... dus x =4 kan nooit een stationaire punt zijn..

Ik ben nu wel mindfucked.

Kan iemand me vertellen hoe je een multinomiaal experiment bepaalt waarbij er geen onderscheid is tussen de groepen? Dus bijvoorbeeld: er is een kaartspel tussen 4 spelers. Elke speler krijgt 13 kaarten. Hoeveel mogelijke verdelingen zijn er als er geen onderscheid is tussen de spelers?

Edit: een kaartspel bestaat uiteraard uit 52 kaarten.

quote:

Op dinsdag 14 oktober 2014 22:24 schreef Wouterw17 het volgende:
Kan iemand me vertellen hoe je een multinomiaal experiment bepaalt waarbij er geen onderscheid is tussen de groepen? Dus bijvoorbeeld: er is een kaartspel tussen 4 spelers. Elke speler krijgt 13 kaarten. Hoeveel mogelijke verdelingen zijn er als er geen onderscheid is tussen de spelers?
Edit: een kaartspel bestaat uiteraard uit 52 kaarten.

52!/(13!13!13!13!4!)?

quote:

Op dinsdag 14 oktober 2014 22:26 schreef Janneke141 het volgende:
[..]
52!/(13!13!13!13!4!)?

Volgens mij is die factor 4! overbodig. En sowieso moet de noemer optellen tot aan de teller.

quote:

Op donderdag 9 oktober 2014 23:52 schreef Bram_van_Loon het volgende:
Het is niet echt iets waarvoor deze draad is bedoeld, helaas misschien, maar het lijkt me aardig om het toch maar eens te doen.

Het lijkt me juist prima om af en toe dit soort dingen te doen. Lees de OP nog even, daar is sprake van passies toch?

quote:

Ik kwam een interessant vraagstuk tegen wat gemakkelijk te begrijpen is maar desalniettemin erg leerzaam is.
Heron's probleem. De vraag. Plaatsen A en B liggen langs een rivier, je moet via die rivier van A naar B. Wat is de kortste weg? Probeer het geometrisch op te lossen als je het zelf probeert, niet met rekenen.

Het is een beetje jammer dat je dit vraagstuk niet in de oorspronkelijke vorm geeft, want die is wel interessanter. Maar eerst iets over de man zelf en zijn werk. Heron van Alexandrië was zeker geen zuiver wiskundige, eerder iemand die je nu een werktuigbouwkundig ingenieur zou noemen, en hij construeerde dan ook diverse toestellen zoals een verkoopautomaat, pompen, en een voorloper van de stoommachine. Als men het belang van deze en soortgelijke uitvindingen had ingezien, dan had de industriële revolutie wellicht 1500 jaar eerder kunnen plaatsvinden. Daarnaast was hij uitstekend op de hoogte met de wiskunde van zijn tijd en leverde hij ook originele bijdragen, zoals een bewijs voor de parallellogramconstructie bij de samenstelling van twee verplaatsingen, oftewel de optelling van vectoren avant la lettre.

Zijn naam is nog verbonden aan de methode van Heron voor het berekenen van vierkantswortels, een methode die echter veel eerder ook al aan de Babyloniërs bekend was. Deze methode komt er (in moderne notatie) op neer dat als x_n een benadering is van √A die iets te klein is, dat A/x_n dan een iets te grote benadering is van √A en vice versa, zodat we dus een betere benadering kunnen krijgen dan de slechtste van deze twee benaderingen door ze te middelen, wat een nieuwe benadering x_n+1 = ½(x_n + A/x_n) geeft. Het is gemakkelijk na te gaan dat deze iteratie equivalent is met de Newton-Raphson iteratie voor √A.

Daarnaast is zijn naam verbonden aan de formule van Heron voor de bepaling van de oppervlakte van een driehoek waarvan de lengtes van de drie zijden zijn gegeven, in moderne notatie



waarin a, b, c de lengtes zijn van de drie zijden, terwijl



de halve omtrek is van de driehoek. De gewoonte om de halve omtrek van een driehoek oftewel de halve som van de zijden (semisumma laterum) aan te geven met de letter s gaat terug op Euler, die ook een bewijs gaf van de formule van Heron. Er zijn veel verschillende bewijzen (meetkundig, algebraïsch, goniometrisch) voor de formule van Heron, maar het originele (en zeer ingenieuze) bewijs van Heron was lange tijd onbekend, totdat in 1896 een manuscript met de complete tekst van zijn Metrica werd ontdekt.

Voor een bespreking van dit bewijs en het overige wiskundige werk van Heron kun je voor een eerste oriëntatie uitstekend terecht in het onvolprezen werk van Sir Thomas Heath, A History of Greek Mathematics (2 dln., Oxford 1921), dat online beschikbaar is (Volume 1, Volume 2). Heath opent zijn hoofdstuk over Heron met de lang omstreden kwestie van de datering van Heron. In 1938 liet Otto Neugebauer echter zien dat een in Heron's werk Dioptra beschreven maansverduistering, waargenomen te Alexandrië, alleen de maansverduistering van 13 maart 62 (Juliaanse kalender) kan zijn geweest, wat dus een terminus post quem oplevert voor het ontstaan van de tekst en daarmee voor het einde van zijn leven. Men neemt nu algemeen aan dat hij heeft geleefd in de eerste eeuw n.C.

Van alle bewaard gebleven werken van Heron is in de periode 1899-1914 bij Teubner in Leipzig een wetenschappelijke uitgave verschenen met een kritisch apparaat, uitvoerige commentaren en inleidingen, alsmede een Duitse vertaling van alle teksten. Deze editie (herdrukt in 1976 bij de destijds West-Duitse divisie van Teubner in Stuttgart) is online beschikbaar via Gallica.

Het vraagstuk dat je aan de orde stelt is in feite een stelling afkomstig uit een werk van Heron dat bekend staat als de Catoptrica, wat al aangeeft dat het handelt over spiegelingen (Gr. κάτοπτρον 'spiegel'). De Griekse tekst is ergens in de middeleeuwen verloren gegaan, maar de Vlaamse geestelijke Willem van Moerbeke heeft er een Latijnse vertaling van gemaakt die wel bewaard is gebleven, zodat we er nu nog kennis van kunnen nemen. In de Teubner editie is de Latijnse tekst van de Catoptrica (met Duitse vertaling) opgenomen in Vol. 2, en de stelling waar het om gaat komt aan de orde in hoofdstuk IV, hier. Heron stelt dat bij een spiegel de gelijkheid van de hoek van inval en de hoek van uitval impliceert dat het licht vanaf een object naar een waarnemer die het object via de spiegel waarneemt de kortst mogelijke weg aflegt.

Uitgaande van het diagram dat je zelf postte kunnen we dit als volgt inzien.



Zij s een rechte en laten A en B twee punten zijn aan dezelfde zijde van de rechte s zodanig dat lijnstuk AB niet loodrecht staat op de rechte s. Zij verder C het spiegelbeeld van A in s. Aangezien de punten A en C en daarmee ook de punten B en C aan weerszijden van de rechte s liggen, snijdt het lijnstuk BC de rechte s in een punt P. Kies nu een willekeurig tweede punt Q ≠ P op de rechte s. Ik beweer nu dat

AP + PB < AQ + QB

Bewijs:

Zij R het snijpunt van lijnstuk AC met de rechte s. Dan is AR = CR en AC ⊥ RP en dus ∠ARP = ∠CRP en daarmee △ARP ≅ △CRP (ZHZ) en dus AP = CP. Evenzo is △ARQ ≅ △CRQ (ZHZ) en dus AQ = CQ. Merk op dat AQ = CQ ook geldt als Q = R aangezien AR = CR. Nu is

AP + PB = CP + PB = CB < CQ + QB = AQ + QB

en dus

AP + PB < AQ + QB

QED

Aangezien △ARP ≅ △CRP is ∠(AP, s) = ∠APR = ∠CPR en aangezien ook (overstaande hoeken) ∠CPR = ∠BPQ = ∠(BP, s) is dus inderdaad

∠(AP, s) = ∠(PB, s)

Het is verder gemakkelijk in te zien dat in de figuur voor △APQ geldt ∠APQ + ∠AQP = (180° − ∠(AP, s)) + ∠(AQ, s) < 180° en daarmee ∠(AQ, s) < ∠(AP, s). Evenzo kunnen we zien dat voor △BPQ geldt ∠BPQ + ∠BQP = ∠(PB, s) + (180° − ∠(QB, s)) < 180° en daarmee ∠(PB, s) < ∠(QB, s). Dus hebben we

∠(AQ, s) < ∠(AP, s) = ∠(PB, s) < ∠(QB, s)

en daarmee ∠(AQ, s) < ∠(QB, s). Uiteraard geldt dit voor een punt Q op de rechte s tussen punt P en het voetpunt van de loodlijn uit punt B op s, maar het is triviaal dat dit eveneens geldt als punt Q samenvalt met het voetpunt van de loodlijn uit B op s of rechts van dit voetpunt op s ligt, aangezien AQ dan hoek PQB deelt. Ligt punt Q daarentegen tussen punt R en punt P, dan kunnen we volkomen analoog laten zien dat ∠(AQ, s) > ∠(QB, s), en uiteraard geldt dit eveneens als punt Q samenvalt met punt R of links daarvan op de rechte s ligt, aangezien QB dan hoek AQP deelt. Daarmee is ∠(AQ, s) ≠ ∠(QB, s) voor elk punt Q op de rechte s anders dan P. De gelijkheid van de hoek van inval en de hoek van uitval impliceert dus inderdaad dat het licht van een object in punt A naar een waarnemer in punt B die het object via de spiegel s waarneemt de kortst mogelijke weg aflegt.

[ Bericht 0% gewijzigd door Riparius op 16-10-2014 14:13:10 ]

quote:

Op dinsdag 14 oktober 2014 21:34 schreef RustCohle het volgende:
Hoi goedenavond,
Zou iemand mij iets kunnen vertellen over de Lagrange functie (waaronder de eerste en de voldoende voorwaarden) en de geometrische interpretatie hiervan? Ik vind het zelf een vrij lastig onderwerp, met name omdat ik niet echt snap waarvoor het dient, want je kunt toch al een maximum/minimum berekenen d.m.v. partieel afgeleiden, waarom zou je de Lagrange functie nodig moeten hebben..? Op internet tref ik veel literatuur wat er al vanuit gaat dat je al een redelijke kennis over het onderwerp beschikt, wat het voor mij lastig maakt.

quote:

Op dinsdag 14 oktober 2014 22:09 schreef Novermars het volgende:
Simpel voorbeeld waarom partiële afgeleides niet nuttig zijn: Stel je hebt de functie gedefinieerd door f(x)=x^2 op het domein A=[2,4]. en je wilt bepalen. Hoe ga je dit doen met partiële afgeleides?
Voor wat extra literatuur. In Simon & Blume's Mathematics for Economists staat heel erg veel beschreven over dit soort problemen.

quote:

Op dinsdag 14 oktober 2014 22:19 schreef RustCohle het volgende:
[..]
Het stationaire punt bepalen door f'(x) te bepalen en vervolgens te kijken wanneer f'(x) = 0 en dan een getallenlijn maken voor de getallen van het domein om zodoende het hoogste punt te bepalen.., het zijn overigens maar 3 getallen.. In dit geval is het maximum bij x= 4 want y= 16 dan. (?)
Misschien spreek ik mijzelf weer tegen, want het stationaire punt is bij x = 0... dus x =4 kan nooit een stationaire punt zijn..
Ik ben nu wel mindfucked.

quote:

Op woensdag 15 oktober 2014 11:15 schreef RustCohle het volgende:
[..]
[..]
[..]

Het probleem is dat aan de rand van het interval de afgeleide niet nul hoeft te zijn om een maximum te hebben.

quote:

Op woensdag 15 oktober 2014 11:24 schreef thenxero het volgende:

[..]

Het probleem is dat aan de rand van het interval de afgeleide niet nul hoeft te zijn om een maximum te hebben.

Hoezo? Dat is toch een noodzakelijje voorwaarde? Daarnaast kun je hier toch geen lagrange op toepassen? Want dat betreft op twee variabelen