SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
Hahahahha nee zeker niet. Had het liefst voor de sier gewild, maar ja.quote:Op maandag 5 mei 2014 17:16 schreef Anoonumos het volgende:
Dat heet de absolute waarde. Die streepjes staan er niet voor de sier.
Ik snap hem niet helemaal... In mijn boek is het zeer kort uitgelegd en op internet is er ook zeer weinig te vinden over de absolute-waardefunctie, althans weinig goede naar mijn mening..
In mijn boek staat er alleen dit:
f(x) = |x| die gedefinieerd is door |x| = x als x > 0 en |x| = -x als x < 0. Voor alle x geldt dat |x|² = x².
Maar ja dan zou ik ervan uit moeten gaan dat |x|³ = -x³ ?
Ja.quote:
[..]
f(x) = |x| die gedefinieerd is door |x| = x als x > 0 en |x| = -x als x < 0.
|x| = - x als x < 0
-0.5 is negatief dus
|-0.5| = - (-0.5) = 0.5
Dus |-0.5| = 0.5
Absolute waarde nemen is niets anders dan een getal positief maken. Als een getal al positief is, dan verandert er niks.
Oh die - bij -x is losstaand wat x zal zijn bij x < 0 ? Dus zoals jij zegt als x = -0,5 dan is het -(-0,5) omdat die - niks te maken heeft met x die <0 kan zijn?quote:
[..]
Ja.
|x| = - x als x < 0
-0.5 is negatief dus
|-0.5| = - (-0.5) = 0.5
Dus |-0.5| = 0.5
Absolute waarde nemen is niets anders dan een getal positief maken. Als een getal al positief is, dan verandert er niks.
In principe los je toch absolute waarde functies twee keer op?quote:
[..]
Ja.
|x| = - x als x < 0
-0.5 is negatief dus
|-0.5| = - (-0.5) = 0.5
Dus |-0.5| = 0.5
Absolute waarde nemen is niets anders dan een getal positief maken. Als een getal al positief is, dan verandert er niks.
Dus x^4 < |x^(1/3)| los je op als volgt:
x^4 - x^(1/3) < 0 en als x^4 + x^(1/3) toch?
Ja precies.quote:
[..]
In principe los je toch absolute waarde functies twee keer op?
Dus x^4 < |x^(1/3)| los je op als volgt:
x^4 - x^(1/3) < 0 en als x^4 + x^(1/3) toch?
Je moet wel opletten dat je dan voor
x^4 - x^(1/3) < 0 alleen naar x ≥ 0 kijkt
en voor
x^4 + x^(1/3) < 0 alleen naar x < 0
Hoe bedoel je? En wat is de gedachte achter dit hele gebeuren waarom je bij absolute waarden altijd dubbel moet gaan oplossen? Geldt dit ook voor even machten of alleen voor oneven machten?quote:
[..]
Ja precies.
Je moet wel opletten dat je dan voor
x^4 - x^(1/3) < 0 alleen naar x ≥ 0 kijkt
en voor
x^4 + x^(1/3) < 0 alleen naar x < 0
Daarnaast snap ik niet wat de bedoeling er dus van is, als alles toch als een positief getal benadert gaat worden...
Vooral dit bijvoorbeeld:
x^(1/n) = | x | als n even is, en x^(1/n) = x als n oneven is..
Ik zie het verschil niet echt...want of het nou | x | of x is, x kan altijd zowel negatief als positief zijn..
x^(1/n) = | x | als n even is, en x^(1/n) = x als n oneven is..
Ik zie het verschil niet echt...want of het nou | x | of x is, x kan altijd zowel negatief als positief zijn..
Dan zou ik toch even een goed boek of internetsite (Of youtube, Khan academy ... ) zoeken die het uitlegt.
Gewoon even vanaf het begin beginnen met de definitie.
Gewoon even vanaf het begin beginnen met de definitie.
Thanks. Ik heb gekeken naar een aantal video's op zowel khan academy als op Youtube, maar de basis is mij geheel duidelijk.. Moeilijkheden beginnen met vergelijkingen:quote:
| 2x + 3 | = 2
Het oplossen is geen probleem, maar het begrijpen ervan.
Ik zal een voorbeeld geven wat ik niet kan begrijpen eraan:
x^4 = | x |
x (x³ - 1)
x = 0 of x = 1^(1/3) zou ik zeggen, maar het is
x = 0 of x = 1 of x = -1
Vind het gewoon al helemaal raar dat (x³ - 1 ) --> x = 1 is ... ik zou denken x³= 1 waardoor x = 1^(1/3)
x^4 = | x |
x (x³ - 1)
x = 0 of x = 1^(1/3) zou ik zeggen, maar het is
x = 0 of x = 1 of x = -1
Vind het gewoon al helemaal raar dat (x³ - 1 ) --> x = 1 is ... ik zou denken x³= 1 waardoor x = 1^(1/3)
hoe kom je opeens aan 1^(1/3)?quote:
Ik zal een voorbeeld geven wat ik niet kan begrijpen eraan:
x^4 = | x |
x (x³ - 1)
x = 0 of x = 1^(1/3) zou ik zeggen, maar het is
x = 0 of x = 1 of x = -1
Vind het gewoon al helemaal raar dat (x³ - 1 ) --> x = 1 is ... ik zou denken x³= 1 waardoor x = 1^(1/3)
oh is blijkbaar gelijk aan 1
[ Bericht 5% gewijzigd door wiskundenoob op 05-05-2014 18:26:03 ]
| -1 | = 1 = 1^4quote:
[..]
(x³ - 1 ) --> ik zou denken x³= 1 waardoor x = 1^(1/3)
| 1 | = 1 = 1^4
| 0 | = 0 = 0^4
1^(1/3) = 1, klopt toch ook? Je moet alleen niet de negatieve oplossing vergeten. Net zoals x²=4 ook twee oplossingen heeft, x=2 en x=-2.quote:
[..]
(x³ - 1 ) --> ik zou denken x³= 1 waardoor x = 1^(1/3)
Wacht, maar het is een derde macht dus -1 is helemaal geen oplossing van x³ - 1 =0
.
ohjaaquote:
[..]
| -1 | = 1 = 1^4
| 1 | = 1 = 1^4
| 0 | = 0 = 0^4
Je snapt dat de derdemachtswortel van een gewoon een is?quote:
Ik zal een voorbeeld geven wat ik niet kan begrijpen eraan:
x^4 = | x |
x (x³ - 1)
x = 0 of x = 1^(1/3) zou ik zeggen, maar het is
x = 0 of x = 1 of x = -1
Vind het gewoon al helemaal raar dat (x³ - 1 ) --> x = 1 is ... ik zou denken x³= 1 waardoor x = 1^(1/3)
En een hint: x^4 = | x | geeft x^4 = x v x^4 = -x
De basis van absolute-waardefuncties is hartstikke makkelijk, maar wanneer er vergelijkingen en ongelijkheden erbij komen kijken, snap ik er niks van..quote:
[..]
1^(1/3) = 1, klopt toch ook? Je moet alleen niet de negatieve oplossing vergeten. Net zoals x²=4 ook twee oplossingen heeft, x=2 en x=-2.
Precies, gewoon deze definitie opschrijven en dat uitwerken. Je moet er wel rekening mee houden dat x^4 = x alleen geldt voor x>=0, en x^4=-x voor x <0.quote:Op maandag 5 mei 2014 18:17 schreef jordyqwerty het volgende:
[..]
Je snapt dat de derdemachtswortel van een gewoon een is?
En een hint: x^4 = | x | geeft x^4 = x v x^4 = -x
Mooie! Dankjewel!quote:
[..]
Je snapt dat de derdemachtswortel van een gewoon een is?
En een hint: x^4 = | x | geeft x^4 = x v x^4 = -x
Denk ik het net te begrijpen gaat het weer fout...quote:
[..]
Precies, gewoon deze definitie opschrijven en dat uitwerken. Je moet er wel rekening mee houden dat x^4 = x alleen geldt voor x>=0, en x^4=-x voor x <0.
x^4 < x^(1/3)
Dus ik doe
x^7 - x want (x^1/3 = x)
en
x^7 + x
dus
x ( x^6 - 1 ) en x (x^6 +1 ) -- > x = 0, x > 1 en x = 0, x < -1
Dus x =0 , x > 1 en x < -1
Hoe ik op die tekens kom?
Gewoon de getallenrij gemaakt:
-------------- -1 ++++++ 0 ----------- 1 +++++++++
Toch blijkt het fout te zijn want het is x < 1 en x > -1
[ Bericht 0% gewijzigd door Super-B op 05-05-2014 18:40:35 ]
quote:
[..]
Denk ik het net te begrijpen gaat het weer fout...
x^4 < x^(1/3)
Dus ik doe
x^7 - x want (x^1/3 = x)
en
x^7 + x
dus
x ( x^6 - 1 ) en x (x^6 +1 ) -- > x = 0, x > 1 en x = 0, x < -1
Dus x =0 , x > 1 en x < -1
Hoe ik op die tekens kom?
Gewoon de getallenrij gemaakt:
-------------- -1 ++++++ 0 ----------- 1 +++++++++
Toch blijkt het fout te zijn want het is x=0, x < 1 en x > -1
x = | x³ |quote:
Los straks even |x^3| = x op, om te zien of je het begrijpt.
x(1 - x²) en x(1 + x³ )
x = 0 of x = -1 (want beide kanten komen uit op -1)
Je tweede vergelijking moet x(1 + x^2 ) zijn.quote:
[..]
x = | x³ |
x(1 - x²) en x(1 + x³ )
x = 0 of x = -1 (want beide kanten komen uit op -1)
En -1 klopt natuurlijk niet. Vul maar in.
Zie daarvoor de opmerking van thenxero
SES / [Bèta wiskunde] Huiswerk- en vragentopic
x³ = |x| geeft x³ = x v x³ = -xquote:
Los straks even |x^3| = x op, om te zien of je het begrijpt.
x(x²-1) v x(x² + 1)
dus x = 0 , x = 1 , x = -1
x³ = x als x ≥ 0quote:
x³ = -x als x < 0
Dus -1 is geen oplossing want je vergelijking x(x²-1) = 0 geldt alleen als x ≥ 0.
Huh?quote:
[..]
x³ = x als x ≥ 0
x³ = -x als x < 0
Dus -1 is geen oplossing want je vergelijking x(x²-1) = 0 geldt alleen als x ≥ 0.
Voor welke x geldt x^3 = |x| ?
Absolute waarde, altijd twee gevallen onderscheiden.
Geval 1: x ≥ 0.
Dan |x| = x.
Voor welke x ≥ 0 geldt x^3 = x oftewel x(x^2 - 1) = 0?
x(x^2 - 1) = 0 oplossen geeft x =0 of x = 1 of x = -1.
Maar we hadden aangenomen dat x ≥ 0 ! Anders mogen we niet zeggen dat |x| = x.
Dus x = 0 en x = 1 zijn oplossingen. Van x = -1 kunnen we nog niet zeggen of het een oplossing is. Daarvoor moeten we naar geval 2 kijken.
Geval 2: x < 0.
Dan |x| = -x.
Voor welke x < 0 geldt x^3 = -x oftewel x(x^2 + 1) = 0?
Voor geen enkele x. Dus we vinden geen extra oplossingen.
Conclusie: x^3 = |x| voor x = 0 en voor x = 1.
Door invullen zien we ook dat x = -1 geen oplossing is.
(-1)^3 = -1
| -1| = 1
En dat is niet gelijk.
quote:
[..]
Wat snap je niet?
(Wow er zijn ineens veel pagina's bijgekomen zeg.)
11:16
Bedankt voor je reactie.. Ik kijk even een video, gepost hierboven.. Ik begrijp er even helemaal niks meer van.quote:
Voor welke x geldt x^3 = |x| ?
Absolute waarde, altijd twee gevallen onderscheiden.
Geval 1: x ≥ 0.
Dan |x| = x.
Voor welke x ≥ 0 geldt x^3 = x oftewel x(x^2 - 1) = 0?
x(x^2 - 1) = 0 oplossen geeft x =0 of x = 1 of x = -1.
Maar we hadden aangenomen dat x ≥ 0 ! Anders mogen we niet zeggen dat |x| = x.
Dus x = 0 en x = 1 zijn oplossingen. Van x = -1 kunnen we nog niet zeggen of het een oplossing is. Daarvoor moeten we naar geval 2 kijken.
Geval 2: x < 0.
Dan |x| = -x.
Voor welke x < 0 geldt x^3 = -x oftewel x(x^2 + 1) = 0?
Voor geen enkele x. Dus we vinden geen extra oplossingen.
Conclusie: x^3 = |x| voor x = 0 en voor x = 1.
Door invullen zien we ook dat x = -1 geen oplossing is.
(-1)^3 = -1
| -1| = 1
En dat is niet gelijk.
Dat ''opsplitsen'' begrijp ik niet, vanaf 11:16 in de video.. Ik denk dat het daar ligt, waar ik de fout in ga.
Correct. This is a bifurcation.quote:
Bifurcartion. Can you define in your own words?
Splitting it up in two statements, yeah. Or the way mathematicians break up with their girlfriends.
That's like their facebookstatus." I've bifurcated! "
Wat een popie jopie Sorry hiervoor.
Ja ik weet het..quote:
[..]
Correct. This is a bifurcation.
Bifurcartion. Can you define in your own words?
Splitting it up in two statements, yeah. Or the way mathematicians break up with their girlfriends.
That's like their facebookstatus." I've bifurcated! "
Sorry hiervoor.
Ik kon even geen uitgebreidere vinden.
Neem de rekenregels voor exponenten eens doorquote:
[..]
Denk ik het net te begrijpen gaat het weer fout...
x^4 < x^(1/3)
Dus ik doe
x^7 - x want (x^1/3 = x)
en
x^7 + x
dus
x ( x^6 - 1 ) en x (x^6 +1 ) -- > x = 0, x > 1 en x = 0, x < -1
Dus x =0 , x > 1 en x < -1
Hoe ik op die tekens kom?
Gewoon de getallenrij gemaakt:
-------------- -1 ++++++ 0 ----------- 1 +++++++++
Toch blijkt het fout te zijn want het is x < 1 en x > -1
Bereken mbv de productregel de afgeleide van:
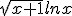
Dus ik kom op:
(1/2) (x+1) ^(-1/2) ln x
+
wortel(x+1)/x
Maar het moet zijn: wortel(x+1)/x + ln x / (2*wortel(x+1))
Wat doe ik verkeerd?
Dus ik kom op:
(1/2) (x+1) ^(-1/2) ln x
+
wortel(x+1)/x
Maar het moet zijn: wortel(x+1)/x + ln x / (2*wortel(x+1))
Wat doe ik verkeerd?
Filmpje bekeken en het wordt steeds duidelijker!quote:
[..]
Neem de rekenregels voor exponenten eens door
x^4 > x³
Dit wordt opgesplitst in
x^4 > x³ en x^4 < -x³
x³(x - 1 ) > 0 en x³(x + 1) < 0
x > 1 en x < -1 echter begrijp ik niet wat ik dus met die 0 moet doen? x =0 , x>0 of x<0 ?
En wat ik ik me afvraag die -x³, stel het is -2 is dat dan -(-2)³ en dus 8 en -2^4 = -16 waardoor dus -x³ groter is dan x^4 ?
Één gedachtenkronkel: waarvoor dient de absolute waardefunctie? Dus waarom zou ik berekenen wanneer x^4< -x³ als het om x^4 > x³ gaat?
Dat is hetzelfde.quote:
Bereken mbv de productregel de afgeleide van:
Dus ik kom op:
(1/2) (x+1) ^(-1/2) ln x
+
wortel(x+1)/x
Maar het moet zijn: wortel(x+1)/x + ln x / (2*wortel(x+1))
Wat doe ik verkeerd?
a-p = 1/apquote:
Bereken mbv de productregel de afgeleide van:
Dus ik kom op:
(1/2) (x+1) ^(-1/2) ln x
+
wortel(x+1)/x
Maar het moet zijn: wortel(x+1)/x + ln x / (2*wortel(x+1))
Wat doe ik verkeerd?
Edit: Ah, iemand was me weer voor
Pff... het antwoord is x > 1 en x < 0 .....quote:
[..]
Filmpje bekeken en het wordt steeds duidelijker!
x^4 > x³
Dit wordt opgesplitst in
x^4 > x³ en x^4 < -x³
x³(x - 1 ) > 0 en x³(x + 1) < 0
x > 1 en x < -1 echter begrijp ik niet wat ik dus met die 0 moet doen? x =0 , x>0 of x<0 ?
En wat ik ik me afvraag die -x³, stel het is -2 is dat dan -(-2)³ en dus 8 en -2^4 = -16 waardoor dus -x³ groter is dan x^4 ?
Één gedachtenkronkel: waarvoor dient de absolute waardefunctie? Dus waarom zou ik berekenen wanneer x^4< -x³ als het om x^4 > x³ gaat?
volgens wolframalpha.comHoe kan dat....
maar volgens het antwoordenmodel heb ik het wel goed met x > 1 en x < -1. Maar ik snap niet hoe x = 0? Omdat het x > 0 en x < 0 is en daarom x=0 is?
Ik doe alles om niet aan bacheloronderzoek en presentaties te hoeven werken op het moment.quote:
[..]
a-p = 1/ap
Edit: Ah, iemand was me weer voor
quote:
Akkoord! Ik heb hem doorquote:
[..]
a-p = 1/ap
Edit: Ah, iemand was me weer voor
Dank heren
Oke, nog een (voor jullie makkelijke) vraag.
Ik kom nu op x * (1/(1^(1/3))) uit.
Dit wordt in het antwoordmodel vereenvoudigt tot 1/3
Maar als ik hem vereenvoudig houd ik ^(1/3) over, hoezo mag je dit herschrijven tot 1/3?
Ik kom nu op x * (1/(1^(1/3))) uit.
Dit wordt in het antwoordmodel vereenvoudigt tot 1/3
Maar als ik hem vereenvoudig houd ik ^(1/3) over, hoezo mag je dit herschrijven tot 1/3?
Hahahaha. Iedereen wordt denk ik wel gek en misselijk van onze vragen.quote:
Oke, nog een (voor jullie makkelijke) vraag.
Ik kom nu op x * (1/(1^(1/3))) uit.
Dit wordt in het antwoordmodel vereenvoudigt tot 1/3
Maar als ik hem vereenvoudig houd ik ^(1/3) over, hoezo mag je dit herschrijven tot 1/3?
als je x^4 < √x hebt en je stelt √x = x
wordt x^4 dan x^8 of x^6? Want zover ik weet is bij vermenigvuldiging dat machten opgeteld worden?
wordt x^4 dan x^8 of x^6? Want zover ik weet is bij vermenigvuldiging dat machten opgeteld worden?
Zoals ik x * (1/(1^(1/3))) lees is het gewoon gelijk aan x. Typo?quote:
Oke, nog een (voor jullie makkelijke) vraag.
Ik kom nu op x * (1/(1^(1/3))) uit.
Dit wordt in het antwoordmodel vereenvoudigt tot 1/3
Maar als ik hem vereenvoudig houd ik ^(1/3) over, hoezo mag je dit herschrijven tot 1/3?
http://www.wolframalpha.com/input/?i=+x+*+%281%2F%281%5E%281%2F3%29%29%29+
