SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d


De manier waarop je dit formuleert geeft mooi je begripsverwarring weer: machtsverheffen is echt iets anders dan vermenigvuldigen met een bepaalde factor. Als je hebtquote:Op woensdag 10 juli 2013 10:00 schreef wiskundenoob het volgende:
Sorry, had het moeten weten dat je niet zomaar bij alle termen met machten mag vermenigvuldigen.
a + b = c
en je hebt een getal p ≠ 0, dan is dit equivalent met
ap + bp = cp
maar uit a + b = c volgt dan niet dat
ap + bp = cp
Immers, als dit wel zo was, dan zou je met p = 2 hebben
a2 + b2 = c2 = (a + b)2
en dit klopt in het algemeen niet, omdat (a + b)2 = a2 + 2ab + b2. Het dubbele product 2ab zorgt ervoor dat a2 + b2 in het algemeen niet hetzelfde is als (a + b)2. Dat zou alleen opgaan als 2ab = 0 zou zijn, en dat is alleen zo als hetzij a = 0 hetzij b = 0.
Het is van het grootste belang dat je in ieder geval de volgende merkwaardige producten van buiten kent en dat je deze bij allerlei algebraïsche herleidingen ook steeds kunt herkennen en kunt toepassen:
(a + b)2 = a2 + 2ab + b2
(a − b)2 = a2 − 2ab + b2
(a + b)(a − b) = a2 − b2
Het gaat hier steeds om de vermenigvuldiging van tweetermen die uit een som (a + b) of een verschil (a − b) van twee grootheden bestaan. Vermenigvuldiging van tweetermen komt erg vaak voor en met de tweetermen (a + b) en (a − b) kun je precies de bovenstaande drie producten vormen. Eigenlijk vier, maar (a − b)(a + b) is uiteraard hetzelfde als (a + b)(a − b) omdat vermenigvuldiging commutatief is.
Belangrijk bij alle identiteiten, en dus ook bij deze merkwaardige producten, is dat je ze zowel van links naar rechts als van rechts naar links kunt herkennen en toepassen. Dus, als je ergens p2 + 2pq + q2 tegenkomt, dan moet je onmiddellijk herkennen dat dit hetzelfde is als (p + q)2. En als je x2 − 6x + 9 ziet staan, dan moet je direct herkennen dat dit hetzelfde is als (x − 3)2.
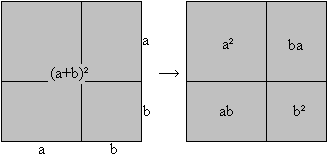
Om deze identiteiten beter te begrijpen en te onthouden, kan het helpen om ze te visualiseren. Als a en b positieve getallen zijn, dan stelt (a + b)2 meetkundig de oppervlakte voor van een vierkant met zijde a + b. Dit vierkant is opgebouwd uit twee kleinere vierkanten met zijde a resp. zijde b, maar ook uit twee rechthoeken met afmeting a bij b, en dus oppervlakte ab, zodat de totale oppervlakte van het vierkant gelijk is aan a2 + 2ab + b2 zoals je hier kunt zien:
Bron
Het is ook mogelijk op deze manier de techniek van het kwadraatafsplitsen voor het oplossen van vierkantsvergelijkingen te visualiseren. Stel dat we de volgende vergelijking hebben:
x2 + 10x = 39
Wat men nu in de oudheid deed was dit opvatten als een vierkant met een onbekende zijde x en een rechthoek van 10 bij x die samen een oppervlakte van 39 eenheden moeten hebben.
De rechthoek van 10 bij x kunnen we verdelen in twee kleinere rechthoeken van 5 bij x die we met de zijde met lengte x tegen twee aangrenzende zijden van het vierkant met zijde x kunnen leggen. Dan krijgen we een L-vormige figuur, zoals je kunt zien. Deze figuur kunnen we aanvullen tot een groot vierkant door er nog een vierkant van 5 bij 5 bij te plaatsen (aangegeven met de stippellijnen in het plaatje). De totale oppervlakte van het grote vierkant wordt dan 39 + 25 = 64, zodat de zijde van het grote vierkant dus 8 moet zijn, want 8·8 = 64. Maar we zien ook dat de zijde van het grote vierkant x + 5 is, zodat dus x = 3 moet zijn.
Uiteraard vind je met deze antieke meetkundige methode alleen de positieve oplossing van de vergelijking, en niet de negatieve oplossing x = −13. Maar dit laat mooi het principe zien van het completeren van het vierkant (completing the square) en je ziet ook waarom kwadratische vergelijkingen nog altijd vierkantsvergelijkingen worden genoemd. En nu begrijp je hopelijk ook beter waarom je bij het oplossen van een vierkantsvergelijking via kwadraatafsplitsing - als althans de kwadratische coëfficiënt één is - de coëfficiënt van x halveert en hier weer het kwadraat van neemt om dit vervolgens bij beide leden op te tellen. Zie verder hier voor meer bijzonderheden.
[ Bericht 0% gewijzigd door Riparius op 10-07-2013 17:48:50 ]


Uh, klopt dat eerste plaatje wel? Waarom is a2 groter dan b2? Waarom zijn a en b niet even groot?
[ Bericht 14% gewijzigd door wiskundenoob op 11-07-2013 14:50:51 ]
[ Bericht 14% gewijzigd door wiskundenoob op 11-07-2013 14:50:51 ]


Ehhh, omdat men dat a priori dient te stellen om de herkomst en afleiding van die merkwaardig product formules inzichtelijk te maken mss? Stel dat a en b idd even groot zouden zijn dan zou je onmiddelijk kunnen stellen:quote:Op donderdag 11 juli 2013 14:27 schreef wiskundenoob het volgende:
Uh, klopt dat eerste plaatje wel? Waarom is a2 groter dan b2? Waarom zijn a en b niet even groot?
a=b => a+b <=> 2a <=> 2b .
(a+b)2 = a2 + 2ab + b2 .
Maar omdat a=b kan je ook gelijk opschrijven:
a2 + 2*a*a + a2 <=> b2 + 2*b*b + b2 <=> 4a2 <=> 4b2
Op eenzelfde manier is aan te tonen dat (a-b)2 = 0 als a=b geldt.


Heb het al begrepen.quote:Op donderdag 11 juli 2013 17:01 schreef VanishedEntity het volgende:
[..]
Ehhh, omdat men dat a priori dient te stellen om de herkomst en afleiding van die merkwaardig product formules inzichtelijk te maken mss? Stel dat a en b idd even groot zouden zijn dan zou je onmiddelijk kunnen stellen:
a=b => a+b <=> 2a <=> 2b .
(a+b)2 = a2 + 2ab + b2 .
Maar omdat a=b kan je ook gelijk opschrijven:
a2 + 2*a*a + a2 <=> b2 + 2*b*b + b2 <=> 4a2 <=> 4b2
Op eenzelfde manier is aan te tonen dat (a-b)2 = 0 als a=b geldt.


Hier ook een paper van een masterstudent waarin de formule van Cardano op soortgelijke (maar natuurlijk wat ingewikkeldere wijze) wordt afgeleid.quote:
Trouwens, ik zoek nog wat opgaven om bewijzen mee te oefenen. Ik heb wel putnam problemen gevonden, maar veel daarvan zijn toch wat te moeilijk voor me. Ik begrijp de te bewijzen stelling wel, maar ik kom eigenlijk nooit uit de bewijzen. Iemand een idee?


Ik ken dat stuk wel, maar ik vind het niet zo goed, zowel inhoudelijk als didactisch niet. Het begint al meteen bij de eerste alinea, waar de auteur de lezer vraagt of deze er wel eens over nagedacht heeft hoe de vergelijkingquote:Op zaterdag 13 juli 2013 01:13 schreef randomo het volgende:
[..]
Hier ook een paper van een masterstudent waarin de formule van Cardano op soortgelijke (maar natuurlijk wat ingewikkeldere wijze) wordt afgeleid.
x3 + 3x2 + 6x + 8 = 0
algebraïsch kan worden opgelost. Dit is een heel slecht voorbeeld, want dergelijke vergelijkingen werden vroeger vaak als oefening in het ontbinden in factoren gegeven. Oplossen van deze vergelijking zonder kennis van de theorie van de kubische vergelijkingen is een koud kunstje omdat je hebt 3x2 + 6x = 3x(x + 2) en x3 + 8 = x3 + 23 = (x + 2)(x2 − 2x + 4) zodat we dus hebben
(x + 2)(x2 + x + 4) = 0
Er staan nogal wat onjuistheden in, zoals de bewering dat Al-Khwarizmi de eerste was die de techniek van kwadraatafsplitsing toepaste. Dat is niet zo, want ca. 1000 jaar eerder werd de techniek al gebruikt door de Grieken, en nog weer zo'n anderhalf millennium eerder (!) was de techniek ook al bekend bij de Babyloniërs, zie hier.
Interessant is dat de Babyloniërs een iets andere methode gebruikten dan de techniek die nu gewoonlijk onder completing the square wordt verstaan. Een bekend voorbeeld is het vraagstuk over een rechthoekig stuk land waarvan de lengte 20 eenheden groter is dan de breedte terwijl de oppervlakte 800 vierkante eenheden bedraagt en waarbij gevraagd wordt de afmetingen van het stuk land te bepalen.
Dit vraagstuk werd opgelost door de helft van het verschil tussen lengte en breedte te nemen, zijnde 10 eenheden, en een strook van deze breedte van de lengte af te halen en aan de breedte toe te voegen. Hierdoor verkrijgen we een L-vormig stuk land dat bestaat uit een vierkant waarvan de zijde het gemiddelde is van de lengte en breedte van het oorspronkelijke stuk land en waaraan een vierkant ontbreekt met een zijde gelijk aan het halve verschil tussen de lengte en breedte van het oorspronkelijke stuk land. Aangezien het L-vormige stuk land dezelfde oppervlakte heeft als het oorspronkelijke rechthoekige stuk land, 800 vierkante eenheden, en het ontbrekende vierkant een oppervlakte heeft van 100 vierkante eenheden, dus samen 900 vierkante eenheden, volgt zo dat het gemiddelde van de gezochte lengte en breedte 30 eenheden bedraagt. De afmetingen van het rechthoekige stuk land bedragen dus 40 bij 20 eenheden.
We kunnen deze werkwijze als volgt vertalen naar een algebraïsche oplossing van het vraagstuk. Noem de gezochte breedte van het stuk land x, dan is de lengte van het stuk land x + 20, en aangezien de oppervlakte 800 bedraagt hebben we dan
x(x + 20) = 800
Het gemiddelde van x en x + 20 is x + 10, en we kunnen nu schrijven x = (x + 10) − 10 en x + 20 = (x + 10) + 10, zodat we de vergelijking kunnen herschrijven als
((x + 10) − 10)((x + 10) + 10) = 800
Nu hebben we het linkerlid omgevormd tot een product van het verschil en de som van twee grootheden, zodat we de vergelijking nu met behulp van het merkwaardig product (a − b)(a + b) = a2 − b2 kunnen herschrijven als
(x + 10)2 − 102 = 800
zodat
(x + 10)2 = 900
waaruit volgt
x = 20 ∨ x = −40
Uiteraard voldoet voor het vraagstuk alleen de positieve oplossing. Deze methode van oplossen van een vierkantsvergelijking wordt wel de Babylonische methode genoemd. Hier wordt dus gebruik gemaakt van het merkwaardig product (a − b)(a + b) = a2 − b2 om het linkerlid te herleiden tot een verschil van twee kwadraten, terwijl bij de gangbare methode gebruik wordt gemaakt van het merkwaardig product (a ± b)2 = a2 ± 2ab + b2 om het linkerlid van de kwadratische vergelijking te completeren tot een volkomen kwadraat.
De (gemoderniseerde) weergave van Bombelli's behandeling van de kubische vergelijking x3 − 15x = 4 is niet juist, Bombelli schreef de oplossing x = 4 namelijk niet als een verschil maar als een som van twee derdemachtswortels uit 2 + √−121 resp. 2 − √−121.
Verder is de notatie i voor √−1 niet ingevoerd door Bombelli, maar pas twee eeuwen later door Euler, die de notatie voor het eerst gebruikte in een paper uit 1777, dat echter pas in 1794 (postuum) werd gepubliceerd. Enkele jaren later, in 1801, introduceerde ook Gauss de notatie i voor √−1, waarbij niet duidelijk is of hij dit onafhankelijk van Euler deed.
Ik mis in het stuk een bespreking van de goniometrische oplossingsmethode voor het geval de kubische vergelijking drie (verschillende) reële wortels heeft. Anders dan de auteur lijkt te willen suggereren is het in dit geval (casus irreducibilis) namelijk in het algemeen niet mogelijk gebruik te maken van de formules van Cardano om langs algebraïsche weg een oplossing te vinden van de kubische vergelijking.
Voor de afleiding van de abc-formule wordt uitgegaan van een afleiding van de pq-formule waaruit door een substitutie p = b/a en q = c/a dan de abc-formule wordt afgeleid. Veel eleganter is echter de directe herleiding van de abc-formule met behulp van de methode van Sridhara. Dit is een gemiste kans omdat het de mogelijkheid had geboden om kwadraatafsplitsing ook te behandelen in het algemene geval waarin de kwadratische coëfficiënt niet gelijk is aan 1 zonder daarbij de vergelijking eerst te herleiden tot de gedaante x2 + px + q = 0.
Geef eens wat voorbeelden van stellingen die je denkt te begrijpen maar waarvan je niet zelf een bewijs kunt verzinnen en (correct) op kunt schrijven.quote:Trouwens, ik zoek nog wat opgaven om bewijzen mee te oefenen. Ik heb wel putnam problemen gevonden, maar veel daarvan zijn toch wat te moeilijk voor me. Ik begrijp de te bewijzen stelling wel, maar ik kom eigenlijk nooit uit de bewijzen. Iemand een idee?
[ Bericht 0% gewijzigd door Riparius op 15-07-2013 04:02:22 ]


wtfquote:Op zaterdag 13 juli 2013 01:13 schreef randomo het volgende:
[..]
Hier ook een paper van een masterstudent waarin de formule van Cardano op soortgelijke (maar natuurlijk wat ingewikkeldere wijze) wordt afgeleid.
Trouwens, ik zoek nog wat opgaven om bewijzen mee te oefenen. Ik heb wel putnam problemen gevonden, maar veel daarvan zijn toch wat te moeilijk voor me. Ik begrijp de te bewijzen stelling wel, maar ik kom eigenlijk nooit uit de bewijzen. Iemand een idee?


Haha inderdaadquote:


Zelfs voor een educational master vind ik het nogal erg matig. Er staat nou niet echt hele moeilijke dingen in. Ik denk dat iedere beta master of bachelor student dit kan schrijven.quote:Op zaterdag 13 juli 2013 10:42 schreef thenxero het volgende:
[..]
Haha inderdaad. Het had ook een matig profielwerkstuk kunnen zijn. Ik hoop dat je hiermee geen wiskunde master kan afronden, maar misschien een education master of zo. Het moet een soort leermethode voor middelbare scholieren voorstellen denk ik.


Ja, klopt. Van die master had ik ook al niet zo'n hoge pet opquote:Op zaterdag 13 juli 2013 10:53 schreef Dale. het volgende:
[..]
Zelfs voor een educational master vind ik het nogal erg matig. Er staat nou niet echt hele moeilijke dingen in. Ik denk dat iedere beta master of bachelor student dit kan schrijven.


Ben ik helemaal met je eens, ik vond het alleen wel mooi om te zien dat de formule ook geometrisch afgeleid kan worden. Bij infi heb ik het geleerd om met een aantal substituties te doen die totaal niet voor de hand liggen, dan vind ik deze manier toch mooier.quote:Op zaterdag 13 juli 2013 05:04 schreef Riparius het volgende:
[..]
Ik ken dat stuk wel, maar ik vind het niet zo goed, zowel inhoudelijk als didactisch niet. Het begint al meteen bij de eerste alinea, waar de auteur de lezer vraagt of deze er wel eens over nagedacht heeft hoe de vergelijking
x3 + 3x2 + 6x + 8 = 0
[...]
O, ik heb er geloof ik nog wel wat liggen, maar dat zijn dus voornamelijk putnam-problemen.quote:Geef eens wat voorbeelden van stellingen die je denkt te begrijpen maar waarvan je niet zelf een bewijs kunt verzinnen en (correct) op kunt schrijven.
Zoals (maar die is volgens mij dan weer achterlijk moeilijk) deze:
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Oh, laat maar. Ik ben net deze site tegengekomen. De makkelijkste daarvan zijn denk ik wel een goede uitdagingEr stond 'project', ik wist niet zeker of dat een thesis was of niet, maar ik vreesde inderdaad al dat het een thesis was... Anyway, het lijkt me ook ontzettend moeilijk om een goede thesis te schrijven, dus als ik dat ooit nog moet gaan doen kom ik misschien ook met zoiets op de proppenquote:


quote:Op zaterdag 13 juli 2013 13:57 schreef randomo het volgende:
[..]
Ben ik helemaal met je eens, ik vond het alleen wel mooi om te zien dat de formule ook geometrisch afgeleid kan worden. Bij infi heb ik het geleerd om met een aantal substituties te doen die totaal niet voor de hand liggen, dan vind ik deze manier toch mooier.
[..]
O, ik heb er geloof ik nog wel wat liggen, maar dat zijn dus voornamelijk putnam-problemen.
Zoals (maar die is volgens mij dan weer achterlijk moeilijk) deze:Bij de UU staat geloof ik 47 ECTS voor je masterthesis. Dan kan je ook wel wat meer dan dat verwachten. Met een dergelijke scriptie ga je het ook echt niet redden, als je even het niveau van wat echte scripties bekijkt: http://studenttheses.libr(...)Sciences&language=nl .SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Oh, laat maar. Ik ben net deze site tegengekomen. De makkelijkste daarvan zijn denk ik wel een goede uitdaging
[..]
Er stond 'project', ik wist niet zeker of dat een thesis was of niet, maar ik vreesde inderdaad al dat het een thesis was... Anyway, het lijkt me ook ontzettend moeilijk om een goede thesis te schrijven, dus als ik dat ooit nog moet gaan doen kom ik misschien ook met zoiets op de proppen


Kan iemand mij uitleggen wat -b/a en c/a betekent bij een kwadratische vergelijking.
[ Bericht 2% gewijzigd door wiskundenoob op 13-07-2013 19:11:45 ]
[ Bericht 2% gewijzigd door wiskundenoob op 13-07-2013 19:11:45 ]


Meestal staat de - staat voor aftrekken, de / voor delen, en a,b voor de coëfficienten van x^2 resp. x, en c de constante term.quote:Op zaterdag 13 juli 2013 14:37 schreef wiskundenoob het volgende:
Kan iemand mij uitleggen wat -b/a en a/c betekent bij een kwadratische vergelijking.


Ja, maar wat reken je dan uit?quote:Op zaterdag 13 juli 2013 14:40 schreef thenxero het volgende:
[..]
Meestal staat de - staat voor aftrekken, de / voor delen, en a,b voor de coëfficienten van x^2 resp. x, en c de constante term.


Dingen afkraken is nogal een kansloze aangelegenheid als je niet eens in staat bent om even op te zoeken waar dat verslag nu daadwerkelijk van is.quote:Op zaterdag 13 juli 2013 10:54 schreef thenxero het volgende:
[..]
Ja, klopt. Van die master had ik ook al niet zo'n hoge pet op.
Het is namelijk onderdeel van een 10 EC vak :http://www.studiegids.sci(...)ourses/course/29529/


Ik kraak het niet af, en ik zei al dat je er misschien een education master mee kan afronden. Desondanks ontstijgt het nauwelijks het pws niveau.quote:Op zaterdag 13 juli 2013 17:10 schreef Thormodo het volgende:
[..]
Zoiets afkraken is nogal een kansloze aangelegenheid als je niet eens in staat bent om even op te zoeken waar dat verslag nu daadwerkelijk van is.
Het is namelijk onderdeel van een 10 EC vak :http://www.studiegids.sci(...)ourses/course/29529/


Ik zeg ook niet dat het een briljant verslag is (alleen al het aantal spelfouten...). Misschien had ik beter Dale kunnen quoten. Overigens is het een onderwijsmodule, dus kunt je moeilijk iets op master niveau gaan maken.quote:Op zaterdag 13 juli 2013 17:15 schreef thenxero het volgende:
[..]
Ik kraak het niet af, en ik zei al dat je er misschien een education master mee kan afronden. Desondanks ontstijgt het nauwelijks het pws niveau.
Daarnaast was mijn PWS van hoger niveau; dat ging over Blackjack & Poker i.c.m. kansrekenen


Dat bedoel ik dusquote:Op zaterdag 13 juli 2013 17:22 schreef Thormodo het volgende:
[..]
Ik zeg ook niet dat het een briljant verslag is (alleen al het aantal spelfouten...). Misschien had ik beter Dale kunnen quoten. Overigens is het een onderwijsmodule, dus kunt je moeilijk iets op master niveau gaan maken.
Daarnaast was mijn PWS van hoger niveau; dat ging over Blackjack & Poker i.c.m. kansrekenen.
En dat ik niet zo'n hoge pet op heb van die master is (misschien niet geheel terecht) gebaseerd op de lesmethodes die ik tegenkom op middelbare scholen. Ik ga er dan even vanuit dat mensen die lesmethodes schrijven wel een master in education hebben. Toch kom ik aan de lopende band didactisch onverantwoorde sommen tegen. Als die master van hoog niveau is dan zou dat niet moeten kunnen.
Ook heb ik een keer gelezen in een blad (kan me de bron niet meer herinneren), dat het niveau van de education master zwaar onder druk stond.


Alleen c is constant, denk ik.quote:Op zaterdag 13 juli 2013 18:27 schreef Thormodo het volgende:
[..]
En toen?
a, b en c zijn gewoon constanten.


Kun je misschien uitleggen waarom je dat denkt en kun je het volledige plaatje geven? Want hier kan uiteraard niemand wat mee.quote:


Bij een kwadratische vergelijking is c volgens mij een constante en het staat ook in de post van thenxero.quote:Op zaterdag 13 juli 2013 18:33 schreef Thormodo het volgende:
[..]
Kun je misschien uitleggen waarom je dat denkt en kun je het volledige plaatje geven? Want hier kan uiteraard niemand wat mee.
Bijv.
x^2 + 10x - 39 = 0
c = -39
[ Bericht 2% gewijzigd door wiskundenoob op 13-07-2013 18:51:33 ]


Heb je het nu over de abc-formule of zo? c = -39 is nogal een rare statement, want er komt verder geen c voor in je post.quote:Op zaterdag 13 juli 2013 18:46 schreef wiskundenoob het volgende:
[..]
Bij een kwadratische vergelijking is c volgens mij een constante en het staat ook in de post van thenxero.
Bijv.
x^2 + 10x - 39 = 0
c = -39
Voor de abc-formule kun je x2 + 10x - 39 in ieder geval zien als ax2 + bx + c. Waarbij a=1, b=10 en c=-39.
Maar nogmaals, het is handig als je het volledige verhaal post...
[ Bericht 0% gewijzigd door Thormodo op 13-07-2013 19:00:32 ]


Ik heb wel een vermoeden waar die het over heeft. Maar zolang hij geen heldere vraag formuleert ga ik er niet meer op in.
Je mag blij zijn dat mensen je willen helpen. Maar als je er zelf geen moeite in steekt, krijg je ook geen moeite terug.
Je mag blij zijn dat mensen je willen helpen. Maar als je er zelf geen moeite in steekt, krijg je ook geen moeite terug.


Ok, dat valt dan wel weer meequote:Op zaterdag 13 juli 2013 17:10 schreef Thormodo het volgende:
[..]
Dingen afkraken is nogal een kansloze aangelegenheid als je niet eens in staat bent om even op te zoeken waar dat verslag nu daadwerkelijk van is.
Het is namelijk onderdeel van een 10 EC vak :http://www.studiegids.sci(...)ourses/course/29529/
Als je nagaat hoe weinig moeite je voor sommige vakken van 7,5 ects hoeft te doen
Klinkt interessantquote:Op zaterdag 13 juli 2013 17:22 schreef Thormodo het volgende:
[..]
Ik zeg ook niet dat het een briljant verslag is (alleen al het aantal spelfouten...). Misschien had ik beter Dale kunnen quoten. Overigens is het een onderwijsmodule, dus kunt je moeilijk iets op master niveau gaan maken.
Daarnaast was mijn PWS van hoger niveau; dat ging over Blackjack & Poker i.c.m. kansrekenen.


Kan je dit toelichten met wat concrete voorbeeldjes? Ik twijfel er niet aan dat je gelijk hebt maar het is handig om het wat concreter te maken.quote:Op zaterdag 13 juli 2013 17:24 schreef thenxero het volgende:
[..]
Dat bedoel ik dus. Het hoeft bij zo'n master natuurlijk ook geen technisch hoogstandje te zijn. Maar je mag wel verwachten dat het historisch correct is, met goede bronnen en zonder spelfouten. Bovendien laat de opbouw ook het een en ander te wensen over.
En dat ik niet zo'n hoge pet op heb van die master is (misschien niet geheel terecht) gebaseerd op de lesmethodes die ik tegenkom op middelbare scholen. Ik ga er dan even vanuit dat mensen die lesmethodes schrijven wel een master in education hebben. Toch kom ik aan de lopende band didactisch onverantwoorde sommen tegen. Als die master van hoog niveau is dan zou dat niet moeten kunnen.
Ook heb ik een keer gelezen in een blad (kan me de bron niet meer herinneren), dat het niveau van de education master zwaar onder druk stond.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL


Wat ik in veel boeken zie is het volgende. Eerst geven ze een "oriënterende som". Het idee is daar dat je gaat nadenken over iets voordat het wordt uitgelegd. In principe is daar nog niks mis mee (alhoewel het niet mijn smaak is, maar dat terzijde). Vervolgens staat er in een "theorie-vakje" (vaak een vrolijk kleurtje met een vrolijk mannetje ernaast) hetgeen wat je hebt uitgevonden in de oriënterende som, maar dan als algemene waarheid.quote:Op zaterdag 13 juli 2013 21:05 schreef Bram_van_Loon het volgende:
[..]
Kan je dit toelichten met wat concrete voorbeeldjes? Ik twijfel er niet aan dat je gelijk hebt maar het is handig om het wat concreter te maken.
Ze laten je bijvoorbeeld f(x)=2x primitiveren tot F(x)=x². Dan mag je F(1)-F(0) uitrekenen en krijg je dus 1 als uitkomst. Je moet ook even herkennen dat het gewoon een driehoekje is en de oppervlakte dus 2*1*1/2 = 1 is. Je ziet dus dat in dit geval de primitieves op 1 en 0 van elkaar afgetrokken gelijk is aan de oppervlakte onder de functie op [0,1]. Vervolgens staat eronder in het "theorie-vakje" simpelweg: De oppervlakte onder de grafiek f van a tot b bepaal je door F(b)-F(a) te berekenen.
Ja, dat is waar. Maar het staat er alsof je met één voorbeeld bewezen hebt dat dat zo is. Alsof je dom bent als je dan nog niet snapt waarom dat altijd waar is. Voor scholieren kan dat best leiden tot onzekerheid, want je weet niet meer wanneer je iets niet snapt of wanneer je het simpelweg niet kán snappen, omdat het niet is uitgelegd.
Een ander voorbeeld. Laatst kwam ik een 'bewijs' tegen waarom de afgeleide van ln(x) gelijk is aan 1/x. Dat ging ongeveer zo (uit mijn hoofd):
Stel y=ex, oftewel x=ln(y). Dan
(1)
Dus ook (?!)
Verder hebben we
Dus
Dus
(Hmm, het originele bewijs was nog erger, want daar werden x en y midden in het bewijs omgewisseld. Totaal overbodig en erg verwarrend. Ik moest het ook drie keer lezen. Ik kan echter niet reproduceren waar ze die wisseltruc deden, dus ik laat het maar zo.)
De (?!) stap vond ik nogal dubieus. Het vereist op zijn minst een rechtvaardiging als je claims maakt als
Bovendien, waarom nou niet gewoon op een heldere manier de kettingregel gebruiken? Ik zou het als volgt doen.
Merk op dat eln(x) = x. Beide kanten differentiëren naar x geeft met de kettingregel:
Dus
Klaar. Niet moeilijker maken dan dat het is!
En zo kan ik helaas nog wel even doorgaan. Nou, nog ééntje dan. Gegeven is een functie f(x) = e-x sin(x). Wat is de periode van deze functie? Beschouw nu g(x)=f(x)^2. Wat is de periode van g?
Nou dan is er alweer een probleem. Ten eerste werd periode in dat boek niet gedefinieerd, maar in mijn ogen is de periode het kleinste getal a zodanig dat f(x+a)=f(x), voor alle x in het domein. Dus wat is dan de periode


Hallo,
ik heb problemen met het begrijpen hoe ik een 'goodness of fit' doe met een Cox regression model. Ik heb via SPSS Cox-Snell residuals verkregen. Als ik papers raadpleeg (http://support.sas.com/re(...)dings13/431-2013.pdf , http://books.google.nl/bo(...)tribution%22&f=false )
dan zou ik een plot moeten krijgen waarbij op de x-axis de residuals staan, maar de y-axis is mij geheel onduidelijk.
Verder zou de residuals moeten lijken op een 'unit exponential distribution', maar ik kan nergens vinden wat de 'unit' toevoegt aan de exponential distribution.. mijn eigen interpretatie is dat het gewoon de exp. distr. is met lambda = 1.
Iemand die misschien toevallig iets af weet van proportional hazard models / cox regression?
Alvast bedankt!
ik heb problemen met het begrijpen hoe ik een 'goodness of fit' doe met een Cox regression model. Ik heb via SPSS Cox-Snell residuals verkregen. Als ik papers raadpleeg (http://support.sas.com/re(...)dings13/431-2013.pdf , http://books.google.nl/bo(...)tribution%22&f=false )
dan zou ik een plot moeten krijgen waarbij op de x-axis de residuals staan, maar de y-axis is mij geheel onduidelijk.
Verder zou de residuals moeten lijken op een 'unit exponential distribution', maar ik kan nergens vinden wat de 'unit' toevoegt aan de exponential distribution.. mijn eigen interpretatie is dat het gewoon de exp. distr. is met lambda = 1.
Iemand die misschien toevallig iets af weet van proportional hazard models / cox regression?
Alvast bedankt!


Sowieso vind ik heel het stelling-bewijs model een beetje, hoe zal ik het zeggen, ongepast (?) voor wiskunde-onderwijs. Een mooi of kort bewijs is vaak compleet wat anders dan een didactisch verantwoord verhaal, en ik zie liever een verhaal dat ik makkelijk onthoud dan een indrukwekkend bewijs, al is het alleen maar omdat ik na het eerste zelf eerder in staat ben zelf een bewijs te produceren.quote:


Het "definitie-stelling-bewijs verhaal" is essentieel voor wiskunde-onderwijs. Door al te veel in Jip- en Janneketaal te werken kan je uitleg op meerdere manieren interpreteren. Het beste werkt het volgens mij om alles zo exact mogelijk te houden en vervolgens met voorbeelden de theorie en de toepassingen te verduidelijken. Zijn kritiek ging echter veel verder dan dat.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL


Volgens mij mis je compleet het punt van mijn post. Bovendien zijn bewijzen niet gemaakt om indruk te wekken, maar om een zo eenvoudig en precies mogelijke redenering te geven. En het lijkt me sterk dat je makkelijker gegoochel onthoudt, dan een simpel bewijsje wat precies voortbouwt op wat je al weet.quote:Op maandag 15 juli 2013 22:46 schreef randomo het volgende:
[..]
Sowieso vind ik heel het stelling-bewijs model een beetje, hoe zal ik het zeggen, ongepast (?) voor wiskunde-onderwijs. Een mooi of kort bewijs is vaak compleet wat anders dan een didactisch verantwoord verhaal, en ik zie liever een verhaal dat ik makkelijk onthoud dan een indrukwekkend bewijs, al is het alleen maar omdat ik na het eerste zelf eerder in staat ben zelf een bewijs te produceren.


Bewijzen zijn niet bedoeld om indruk te wekken, maar vaak wordt er wel een zo kort mogelijk bewijs gegeven, waar je dan weer niet zoveel van leert. Een groot deel van mijn studieboeken en dictaten bestaat uit stellingen en bewijzen, en volgens mij kan de ruimte in veel gevallen beter gebruikt worden.quote:Op dinsdag 16 juli 2013 11:29 schreef thenxero het volgende:
[..]
Volgens mij mis je compleet het punt van mijn post. Bovendien zijn bewijzen niet gemaakt om indruk te wekken, maar om een zo eenvoudig en precies mogelijke redenering te geven. En het lijkt me sterk dat je makkelijker gegoochel onthoudt, dan een simpel bewijsje wat precies voortbouwt op wat je al weet.
Volgens mij is het meer een soort tik die veel wiskundigen hebben, om bij elke stelling een bewijs neer te zetten, ook al is het bewijs op zich niet zo leerzaam. Dan vind ik een 'bewijsschets' geven in veel gevallen nog mooier, omdat je studenten wel snel een idee geeft hoe het bewijs werkt, maar het nog steeds makkelijk leesbaar blijft.
Mijn post was inhoudelijk ook niet echt een reactie op jouw post, meer een licht gerelateerde ergernis die ik soms wel eens heb. Ik zal eens kijken of ik een voorbeeld kan vinden, dan kan ik het misschien wat duidelijker maken.


dan kan sneller; moet je alleen wel differentialen gehad hebbenquote:Op zaterdag 13 juli 2013 21:53 schreef thenxero het volgende:
[..]
Wat ik in veel boeken zie is het volgende. Eerst geven ze een "oriënterende som". Het idee is daar dat je gaat nadenken over iets voordat het wordt uitgelegd. In principe is daar nog niks mis mee (alhoewel het niet mijn smaak is, maar dat terzijde). Vervolgens staat er in een "theorie-vakje" (vaak een vrolijk kleurtje met een vrolijk mannetje ernaast) hetgeen wat je hebt uitgevonden in de oriënterende som, maar dan als algemene waarheid.
Ze laten je bijvoorbeeld f(x)=2x primitiveren tot F(x)=x². Dan mag je F(1)-F(0) uitrekenen en krijg je dus 1 als uitkomst. Je moet ook even herkennen dat het gewoon een driehoekje is en de oppervlakte dus 2*1*1/2 = 1 is. Je ziet dus dat in dit geval de primitieves op 1 en 0 van elkaar afgetrokken gelijk is aan de oppervlakte onder de functie op [0,1]. Vervolgens staat eronder in het "theorie-vakje" simpelweg: De oppervlakte onder de grafiek f van a tot b bepaal je door F(b)-F(a) te berekenen.
Ja, dat is waar. Maar het staat er alsof je met één voorbeeld bewezen hebt dat dat zo is. Alsof je dom bent als je dan nog niet snapt waarom dat altijd waar is. Voor scholieren kan dat best leiden tot onzekerheid, want je weet niet meer wanneer je iets niet snapt of wanneer je het simpelweg niet kán snappen, omdat het niet is uitgelegd.
Een ander voorbeeld. Laatst kwam ik een 'bewijs' tegen waarom de afgeleide van ln(x) gelijk is aan 1/x. Dat ging ongeveer zo (uit mijn hoofd):
Stel y=ex, oftewel x=ln(y). Dan
(1)
Dus ook (?!)
Verder hebben we
Dus
Dus
(Hmm, het originele bewijs was nog erger, want daar werden x en y midden in het bewijs omgewisseld. Totaal overbodig en erg verwarrend. Ik moest het ook drie keer lezen. Ik kan echter niet reproduceren waar ze die wisseltruc deden, dus ik laat het maar zo.)
De (?!) stap vond ik nogal dubieus. Het vereist op zijn minst een rechtvaardiging als je claims maakt als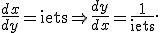
Bovendien, waarom nou niet gewoon op een heldere manier de kettingregel gebruiken? Ik zou het als volgt doen.
Merk op dat eln(x) = x. Beide kanten differentiëren naar x geeft met de kettingregel:
Dus
Klaar. Niet moeilijker maken dan dat het is!
En zo kan ik helaas nog wel even doorgaan. Nou, nog ééntje dan. Gegeven is een functie f(x) = e-x sin(x). Wat is de periode van deze functie? Beschouw nu g(x)=f(x)^2. Wat is de periode van g?
Nou dan is er alweer een probleem. Ten eerste werd periode in dat boek niet gedefinieerd, maar in mijn ogen is de periode het kleinste getal a zodanig dat f(x+a)=f(x), voor alle x in het domein. Dus wat is dan de periode?
f(x)=ln(x)
Stel ln(x)=t => x=e^t
Bereken dy/dx: d(ln(x))/dx = dt/d(et) = 1dt/etdt = 1dt/etdt = 1/et = 1/x


Vaak wordt ln(x) = ∫1x t-1dt geïntroduceerd als deze integraal en dan volgt direct uit de hoofdstelling van de integraalrekening dat d(ln(x))/dx = 1/x. Daarna kan dan exp(x) gedefinieerd worden als de inverse functie van ln(x) en volgt met de kettingregel ook gemakkelijk dat d(exp(x))/dx = exp(x).quote:Op zaterdag 13 juli 2013 21:53 schreef thenxero het volgende:
[..]
Een ander voorbeeld. Laatst kwam ik een 'bewijs' tegen waarom de afgeleide van ln(x) gelijk is aan 1/x. Dat ging ongeveer zo (uit mijn hoofd):
Dit ligt meer voor de hand dan de omgekeerde weg volgen en eerst de afgeleide van ax behandelen (met a > 0), want om aan te tonen dat d(ax)/dx = ln(a)·ax heb je sowieso natuurlijke logarithmen nodig en zou je ook eerst aan moeten tonen dat limh→0 (ah − 1)/h = ln(a).


Helemaal mee eens. limh→0 (ah − 1)/h = ln(a) werd ook nergens aangetoond.quote:Op woensdag 17 juli 2013 16:47 schreef Riparius het volgende:
[..]
Vaak wordt ln(x) = ∫1x t-1dt geïntroduceerd als deze integraal en dan volgt direct uit de hoofdstelling van de integraalrekening dat d(ln(x))/dx = 1/x. Daarna kan dan exp(x) gedefinieerd worden als de inverse functie van ln(x) en volgt met de kettingregel ook gemakkelijk dat d(exp(x))/dx = exp(x).
Dit ligt meer voor de hand dan de omgekeerde weg volgen en eerst de afgeleide van ax behandelen (met a > 0), want om aan te tonen dat d(ax)/dx = ln(a)·ax heb je sowieso natuurlijke logarithmen nodig en zou je ook eerst aan moeten tonen dat limh→0 (ah − 1)/h = ln(a).


Overigens kan ik het wel met de hand uitrekenen, de primitieve is immers bekend. Maar even in mijn GR gegooid, het antwoord voldoet weinig aan de verwachtingen.


WolframAlpha snapt dit prima, maar jij voert het kennelijk verkeerd in, kijk maar hoe het wel werkt.quote:


Wat is er dan precies mis met mijn stukje LaTeX (of TeX, hoe die code ook mag heten)?quote:Op woensdag 17 juli 2013 17:08 schreef Riparius het volgende:
[..]
WolframAlpha snapt dit prima, maar jij voert het kennelijk verkeerd in, kijk maar hoe het wel werkt.
| 1 | 1-4(\int_0^1(\sqrt{1-x^2})dx - 2\int_0^{1/2}(\sqrt{1-x^2})dx) |
[ Bericht 5% gewijzigd door #ANONIEM op 17-07-2013 17:22:42 ]


Niets, en als ik dat invoer in WolframAlpha werkt het ook, dus kennelijk had je dan eerst iets anders.quote:Op woensdag 17 juli 2013 17:18 schreef Amoeba het volgende:
[..]
Wat is er dan precies mis met mijn stukje LaTeX (of TeX, hoe die code ook mag heten)?
[ code verwijderd ]


Amoeba, wat voor cijfer heb jij gekregen voor jouw PWS?
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL


Een 7 man. Ik voel me hard genaaid.quote:Op woensdag 17 juli 2013 18:51 schreef Bram_van_Loon het volgende:
Amoeba, wat voor cijfer heb jij gekregen voor jouw PWS?
Nu snap ik er ook niks meer van. Net kon hij er niet veel van maken.quote:Op woensdag 17 juli 2013 18:47 schreef Riparius het volgende:
[..]
Niets, en als ik dat invoer in WolframAlpha werkt het ook, dus kennelijk had je dan eerst iets anders.


Zo'n havist had last minute 10 uur werk erin gestoken en ontvangt een 9. Ik heb hier tantoe hard voor na zitten denken en krijg een 7. Het leven is een partij oneerlijk.quote:


Je moet maar opzoeken hoeveel geld een theoretische wiskundige verdient voor het aantal uren dat hij van zijn leven erin stopt.quote:Op woensdag 17 juli 2013 19:37 schreef Amoeba het volgende:
[..]
Zo'n havist had last minute 10 uur werk erin gestoken en ontvangt een 9. Ik heb hier tantoe hard voor na zitten denken en krijg een 7. Het leven is een partij oneerlijk.
Hoe theoretischer een wiskundige is, hoe harder hij genaaid wordt.
Ik wil trouwens best je pws lezen, want nu ben ik wel benieuwd.
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.


Beide kanten vermenigvuldigen met 2x+a.quote:Op donderdag 18 juli 2013 20:03 schreef Rezania het volgende:
[ afbeelding ]
[ afbeelding ]
De opgave is duidelijk, dat je met de discriminant moet werken ook. Maar waar halen ze die derde vergelijking vandaan? Het is namelijk geen herleiding, want als je ze plot krijgt je twee andere grafieken.


Ohh, zo.quote:Op donderdag 18 juli 2013 20:39 schreef thenxero het volgende:
[..]
Beide kanten vermenigvuldigen met 2x+a.
Gist is liefde, gist is leven. Vooral in een vagijn.


Nog een vraagje. (Sorry, het is allemaal een beetje weggezakt de laatste tijd.  )
)
Ik wil een breuk primitiveren;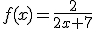
Dan krijg je sowieso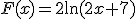 , maar ik heb het idee dat dit nog niet compleet is. Ik heb heel sterk de neiging om te concluderen dat je nog wat met die
, maar ik heb het idee dat dit nog niet compleet is. Ik heb heel sterk de neiging om te concluderen dat je nog wat met die 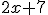 moet doen, maar wat ook al weer?
moet doen, maar wat ook al weer?
Ik wil een breuk primitiveren;
Dan krijg je sowieso
Gist is liefde, gist is leven. Vooral in een vagijn.


Je zit in de buurt. Als je de "primitieve" differentieert (met kettingregel!) dan zie je dat je niet de originele functie terugkrijgt: je zit er een constante naast.quote:Op donderdag 18 juli 2013 21:09 schreef Rezania het volgende:
Nog een vraagje. (Sorry, het is allemaal een beetje weggezakt de laatste tijd.)
Ik wil een breuk primitiveren;
Dan krijg je sowieso, maar ik heb het idee dat dit nog niet compleet is. Ik heb heel sterk de neiging om te concluderen dat je nog wat met die
moet doen, maar wat ook al weer?


Ah ja, differentiëren om de primitieve te controleren, dat is wel handig.quote:Op donderdag 18 juli 2013 21:26 schreef thenxero het volgende:
[..]
Je zit in de buurt. Als je de "primitieve" differentieert (met kettingregel!) dan zie je dat je niet de originele functie terugkrijgt: je zit er een constante naast.
Gist is liefde, gist is leven. Vooral in een vagijn.


Ik ben mijn USB stick met het origineel kwijtgeraaktquote:Op donderdag 18 juli 2013 15:27 schreef Mathemaat het volgende:
[..]
Je moet maar opzoeken hoeveel geld een theoretische wiskundige verdient voor het aantal uren dat hij van zijn leven erin stopt.
Hoe theoretischer een wiskundige is, hoe harder hij genaaid wordt.
Ik wil trouwens best je pws lezen, want nu ben ik wel benieuwd.
Dit is een van de laatste versies. Er kan dus nog ergens een typo ofzo instaan, maar het geeft een idee.
Je hebt DM.. Mijn naam en toenaam staan erbij namelijk.


Het enige wat je fout deed was die vermenigvuldiging met 2 ervoor zetten. Differentïeren van ln(2x+7) met de kettingregel geeft 1/(2x+7) * [2x+7]' = 1/(2x+7) * 2 = 2/(2x+7)quote:
Je kon dit direct zien doordat 2 de afgeleide is van 2x+7. Dat je dat direct herkent, daar willen ze uiteindelijk naartoe.


Ja, dat had ik me ook al bedacht.quote:Op vrijdag 19 juli 2013 06:35 schreef Amoeba het volgende:
[..]
Het enige wat je fout deed was die vermenigvuldiging met 2 ervoor zetten. Differentïeren van ln(2x+7) met de kettingregel geeft 1/(2x+7) * [2x+7]' = 1/(2x+7) * 2 = 2/(2x+7)
Je kon dit direct zien doordat 2 de afgeleide is van 2x+7. Dat je dat direct herkent, daar willen ze uiteindelijk naartoe.
Gist is liefde, gist is leven. Vooral in een vagijn.


[ Bericht 100% gewijzigd door Bram_van_Loon op 19-07-2013 14:00:23 ]
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL


Bedoel je die bijna laatste gelijkheid?quote:Op vrijdag 19 juli 2013 20:38 schreef Rezania het volgende:
Ik ben weer ergens op vastgelopen, gonio deze keer.
[ afbeelding ]
[ afbeelding ]
Hoe komen zij aan?
Daar kun je 0,5*cos(x)*(3 + sin(2x)) namelijk uitschrijven (dus zonder de haakjes om 3 + sin(2x)) en dan kun je zien dat er wat weg valt. Vervolgens kun je er weer haakjes omheen bouwen.


Oh, gewoon herleiden en dan ontbinden in factoren dus? Ik dacht dat het iets met de goniometrieregels had te maken.quote:Op vrijdag 19 juli 2013 20:54 schreef Thormodo het volgende:
[..]
Bedoel je die bijna laatste gelijkheid?
Daar kun je 0,5*cos(x)*(3 + sin(2x)) namelijk uitschrijven (dus zonder de haakjes om 3 + sin(2x)) en dan kun je zien dat er wat weg valt. Vervolgens kun je er weer haakjes omheen bouwen.
Gist is liefde, gist is leven. Vooral in een vagijn.


Even een vraagje over verzamelingenleer. Klopt het dat het supremum niets anders is dan de grootste bovengrens en het infinum de kleinste ondergrens?


Bijna goedquote:Op zaterdag 20 juli 2013 19:22 schreef De-Haas het volgende:
Even een vraagje over verzamelingenleer. Klopt het dat het supremum niets anders is dan de grootste bovengrens en het infinum de kleinste ondergrens?


Dus bijvoorbeeld, [0,1) heeft geen maximum. (Want stel er is een maximum x. Dan geldt x < x+(1-x)/2 <1, tegenspraak.) Maar het supremum is 1. In dit geval is het infumum en het minimum 0.quote:Op zaterdag 20 juli 2013 19:29 schreef Wolfje het volgende:
[..]
Bijna goed, het supremum is de kleinste bovengrens en infimum is de grootste ondergrens.


Zo voelde ik me ook. Ik heb uiteindelijk een wiskundig getint PWS ingeleverd, maar het werd nagekeken door een biologiedocent, en die hield niet van wiskundequote:
Gelukkig uiteindelijk nog wel een 8 gekregen, maar ik hoorde van mensen dat ze in één dag een PWS in elkaar geflanst hebben en ook een 8 hadden.
Wolfram Alpha derpt soms, heb ik ook weleens last van gehad. Ik denk dat je browser opnieuw opstarten kan helpen. Ik kan me voorstellen dat ze verschillende servers hebben met verschillende versies software, en dat het daardoor komt.quote:[..]
Nu snap ik er ook niks meer van. Net kon hij er niet veel van maken.


Mensen die beweren er 1 dag aan gewerkt te hebben zijn van die nerdjes die stiekem al 2 jaar bezig zijn met voorbereiden. 


Dan hebben ze het gewoon met flink wat knip- en plakwerk bij elkaar gesprokkeld vanaf internet. Een beetje docent ziet dat meteen, alleen al door de wisselende schrijfstijlen of het inconsequente gebruik van notaties of een gebrekkige opbouw van het geheel, maar waarschijnlijk zijn er ook veel docenten die de kantjes eraf lopen en het wel best vinden, of geen zin hebben zich erin te verdiepen omdat het buiten hun eigenlijke vakgebied ligt, en dan krijg je dit soort 'beoordelingen'.quote:Op zondag 21 juli 2013 00:29 schreef randomo het volgende:
[..]
Gelukkig uiteindelijk nog wel een 8 gekregen, maar ik hoorde van mensen dat ze in één dag een PWS in elkaar geflanst hebben en ook een 8 hadden.
Ik denk het niet, heb er geen last van. WolframAlpha gebruikt inderdaad verschillende servers, maar ik heb nooit verschillen bemerkt. Wel is er het probleem dat de eerste paar karakters die je typt vaak niet doorkomen als je de hoofdpagina van WolframAlpha oproept en direct iets invoert. Als je dan niet oplet wat je precies invoert dan kan het inderdaad gemakkelijk gebeuren dat WolframAlpha de syntaxis niet begrijpt of verkeerd interpreteert.quote:[..]
Wolfram Alpha derpt soms, heb ik ook weleens last van gehad. Ik denk dat je browser opnieuw opstarten kan helpen. Ik kan me voorstellen dat ze verschillende servers hebben met verschillende versies software, en dat het daardoor komt.


Ja dat bedoelde ik, schreef het alleen verkeerd op. Bedankt in ieder geval.quote:Op zaterdag 20 juli 2013 19:29 schreef Wolfje het volgende:
[..]
Bijna goed, het supremum is de kleinste bovengrens en infimum is de grootste ondergrens.
Ja, afhankelijk van of de grenzen ook in de verzameling zitten zit het supremum/infinum dus wel/niet zelf in de verzameling. Bedankt voor de reactie.quote:Op zaterdag 20 juli 2013 20:03 schreef thenxero het volgende:
[..]
Dus bijvoorbeeld, [0,1) heeft geen maximum. (Want stel er is een maximum x. Dan geldt x < x+(1-x)/2 <1, tegenspraak.) Maar het supremum is 1. In dit geval is het infumum en het minimum 0.


Ik heb het maar één keer gehad (maar ik heb wolfram best vaak gebruikt), maar ik weet wel zeker dat ik het toen niet verkeerd heb ingetypt (ik had het toen van een link). Maargoed, voor hetzelfde geld ging er iets anders fout op de server, daar valt verder niet zoveel over te zeggen.quote:Op zondag 21 juli 2013 01:04 schreef Riparius het volgende:
Ik denk het niet, heb er geen last van. WolframAlpha gebruikt inderdaad verschillende servers, maar ik heb nooit verschillen bemerkt. Wel is er het probleem dat de eerste paar karakters die je typt vaak niet doorkomen als je de hoofdpagina van WolframAlpha oproept en direct iets invoert. Als je dan niet oplet wat je precies invoert dan kan het inderdaad gemakkelijk gebeuren dat WolframAlpha de syntaxis niet begrijpt of verkeerd interpreteert.


Boh, site is down. Het zijn nog best leuke problemen, ik heb er van de problemen van 2000 redelijk wat gemaakt, maar ik weet niet hoeveel ik er goed hebquote:Op zaterdag 13 juli 2013 13:57 schreef randomo het volgende:
[...]
Oh, laat maar. Ik ben net deze site tegengekomen. De makkelijkste daarvan zijn denk ik wel een goede uitdaging


Voor mijn PWS op de havo was ik maar 8 uurtjes bezig. Op de vwo was het een ander verhaal.quote:Op zondag 21 juli 2013 00:50 schreef thenxero het volgende:
Mensen die beweren er 1 dag aan gewerkt te hebben zijn van die nerdjes die stiekem al 2 jaar bezig zijn met voorbereiden.
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.


Opgave 4
Laat zien dat voor alle x > 0 geldt dat sin(x) < x.
Hint: sin(x) = sin(x) - sin(0)
sin(x) heeft een maximum van 1 (voor x = 1/2 π)
Dus als ik aan kan tonen dat x > sin(x) voor x (0,1] dan heb ik in feite de opgave aangetoond. Nu wil ik dit aantonen dmv de differentiaalrekening. Als ik kan aantonen dat d(sin(x))/dx op het interval (0,1] nooit groter is dan 1 is dit toch gelukt? Immers, x stijgt constant met een richtingscoëfficient van 1.
dus:
d(sin(x))/dx = cos(x)
cos(x) = 1
x = 0 ^ x = 2π
Zouden ze dit op een tentamen pikken?
[ Bericht 0% gewijzigd door #ANONIEM op 22-07-2013 23:50:44 ]
Laat zien dat voor alle x > 0 geldt dat sin(x) < x.
Hint: sin(x) = sin(x) - sin(0)
sin(x) heeft een maximum van 1 (voor x = 1/2 π)
Dus als ik aan kan tonen dat x > sin(x) voor x (0,1] dan heb ik in feite de opgave aangetoond. Nu wil ik dit aantonen dmv de differentiaalrekening. Als ik kan aantonen dat d(sin(x))/dx op het interval (0,1] nooit groter is dan 1 is dit toch gelukt? Immers, x stijgt constant met een richtingscoëfficient van 1.
dus:
d(sin(x))/dx = cos(x)
cos(x) = 1
x = 0 ^ x = 2π
Zouden ze dit op een tentamen pikken?
[ Bericht 0% gewijzigd door #ANONIEM op 22-07-2013 23:50:44 ]


Je hebt het denk ik over het interval (0, pi/2]. Ik weet niet of ze dit pikken. Wat namelijk nog wel een beetje sneaky is, is dat in het punt 0 de afgeleides hetzelfde zijn. Dus misschien is er nog een punt x>0 ("heeeel dicht bij 0") zodat sin(x)=x. Dat mag niet, want je moet strikte ongelijkheid aantonen. Daar zou je dan nog wat voor moeten bedenken... als je het echt netjes wil doen.quote:Op maandag 22 juli 2013 23:49 schreef Amoeba het volgende:
Opgave 4
Laat zien dat voor alle x > 0 geldt dat sin(x) < x.
Hint: sin(x) = sin(x) - sin(0)
sin(x) heeft een maximum van 1 (voor x = 1/2 π)
Dus als ik aan kan tonen dat x > sin(x) voor x (0,1] dan heb ik in feite de opgave aangetoond. Nu wil ik dit aantonen dmv de differentiaalrekening. Als ik kan aantonen dat d(sin(x))/dx op het interval (0,1] nooit groter is dan 1 is dit toch gelukt? Immers, x stijgt constant met een richtingscoëfficient van 1.
dus:
d(sin(x))/dx = cos(x)
cos(x) = 1
x = 0 ^ x = 2π
Zouden ze dit op een tentamen pikken?


Voor welke vak is dit? Je moet overigens aantonen dat de afgeleide op het interval (0,pi/2] strikt kleiner is dan één. Dan is het goed. Je kunt het netjes maken met Riemann integratie of met de limietdefinitie van afgeleiden, de tweede is makkelijker.quote:Op maandag 22 juli 2013 23:49 schreef Amoeba het volgende:
Opgave 4
Laat zien dat voor alle x > 0 geldt dat sin(x) < x.
Hint: sin(x) = sin(x) - sin(0)
sin(x) heeft een maximum van 1 (voor x = 1/2 π)
Dus als ik aan kan tonen dat x > sin(x) voor x (0,1] dan heb ik in feite de opgave aangetoond. Nu wil ik dit aantonen dmv de differentiaalrekening. Als ik kan aantonen dat d(sin(x))/dx op het interval (0,1] nooit groter is dan 1 is dit toch gelukt? Immers, x stijgt constant met een richtingscoëfficient van 1.
dus:
d(sin(x))/dx = cos(x)
cos(x) = 1
x = 0 ^ x = 2π
Zouden ze dit op een tentamen pikken?
[ Bericht 2% gewijzigd door Mathemaat op 23-07-2013 00:30:36 ]
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.


Het punt 0 heeft niets van doen met de hele vraag, daar het punt 0 buiten het gevraagde interval valt.quote:Op dinsdag 23 juli 2013 00:14 schreef thenxero het volgende:
[..]
Je hebt het denk ik over het interval (0, pi/2]. Ik weet niet of ze dit pikken. Wat namelijk nog wel een beetje sneaky is, is dat in het punt 0 de afgeleides hetzelfde zijn. Dus misschien is er nog een punt x>0 ("heeeel dicht bij 0") zodat sin(x)=x. Dat mag niet, want je moet strikte ongelijkheid aantonen. Daar zou je dan nog wat voor moeten bedenken... als je het echt netjes wil doen.
http://fooplot.com/plot/oqbbqj2gop
Hier kun je zien wat ik bedoel. Ik zeg dat voor iedere x > 1 het evident is dat sin(x) < x, want sin(x) heeft een maximum van 1.
Dus als aan kan tonen dat op het interval (0, 1] geldt dat sin(x) nooit meer toeneemt dan y = x (met rc = 1 ), dan heb ik toch aangetoond dat sin(x) < x voor x (0, 1]? Immers, sin(x) = x voor x = 0 want dan sin(x) = 0.
y = x neemt constant toe. Als ik aantoon dat sin(x) nooit meer toeneemt op het interval (0,1] dan y = x ben ik toch klaar?quote:Dus misschien is er nog een punt x>0 ("heeeel dicht bij 0") zodat sin(x)=x. Dat mag niet, want je moet strikte ongelijkheid aantonen.
[ Bericht 7% gewijzigd door #ANONIEM op 23-07-2013 00:52:13 ]


Weet ik veel, calculus ofzo. Ik had ergens een vel met wat vragen gevonden en was uit pure verveling maar begonnen met het oplossen van de vragen.quote:Op dinsdag 23 juli 2013 00:14 schreef Mathemaat het volgende:
[..]
Voor welke vak is dit? Je moet overigens aantonen dat de afgeleide op het interval (0,pi/2] strikt kleiner is dan één. Dan is het goed. Je kunt het netjes maken met Riemann integratie of met de limietdefinitie van afgeleiden, de tweede is makkelijker.
http://www.win.tue.nl/~fransm/onderwijs/2DL00/Inhoud.pdf
[ Bericht 8% gewijzigd door #ANONIEM op 23-07-2013 00:46:55 ]


Ik begrijp je wel, maar jij begrijpt mij niet. En het feit dat je er zelf nog je vraagtekens bij zet, suggereert al dat het niet een 100% rigoreus bewijs is. Aangezien calculus vaak niet 100% rigoreus is zal het daar wel voldoen. Bij een analysevak krijg je er geen punten voor.quote:Op dinsdag 23 juli 2013 00:41 schreef Amoeba het volgende:
[..]
Het punt 0 heeft niets van doen met de hele vraag, daar het punt 0 buiten het gevraagde interval valt.
http://fooplot.com/plot/oqbbqj2gop
Hier kun je zien wat ik bedoel. Ik zeg dat voor iedere x > 1 het evident is dat sin(x) < x, want sin(x) heeft een maximum van 1.
Dus als aan kan tonen dat op het interval (0, 1] geldt dat sin(x) nooit meer toeneemt dan y = x (met rc = 1 ), dan heb ik toch aangetoond dat sin(x) < x voor x (0, 1]? Immers, sin(x) = x voor x = 0 want dan sin(x) = 0.
[..]
y = x neemt constant toe. Als ik aantoon dat sin(x) nooit meer toeneemt op het interval (0,1] dan y = x ben ik toch klaar?


Daarom post ik het ook hier. Verder dan dit kom ik met het vwo niet, althans, niet met het gebruik van de differentiaalrekening.quote:Op dinsdag 23 juli 2013 01:00 schreef thenxero het volgende:
[..]
Ik begrijp je wel, maar jij begrijpt mij niet. En het feit dat je er zelf nog je vraagtekens bij zet, suggereert al dat het niet een 100% rigoreus bewijs is. Aangezien calculus vaak niet 100% rigoreus is zal het daar wel voldoen. Bij een analysevak krijg je er geen punten voor.
Zou je me het ontbrekende deel uit kunnen leggen?


Bij de analysevakken krijg je netjes geleerd hoe netjes dingen op moet schrijven. Dat kun je niet even uitleggen.quote:Op dinsdag 23 juli 2013 01:05 schreef Amoeba het volgende:
[..]
Daarom post ik het ook hier. Verder dan dit kom ik met het vwo niet, althans, niet met het gebruik van de differentiaalrekening.
Zou je me het ontbrekende deel uit kunnen leggen?
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.


Oké.quote:Op dinsdag 23 juli 2013 01:12 schreef Mathemaat het volgende:
[..]
Bij de analysevakken krijg je netjes geleerd hoe netjes dingen op moet schrijven. Dat kun je niet even uitleggen.
Had je nog naar m'n profielwerkstuk gekeken?


Ja, het zag er idd interessant uit. Maar ik heb niet zoveel verstand van profielwerkstukken, dus ik kan er niet zoveel over zeggen .quote:Op dinsdag 23 juli 2013 01:12 schreef Amoeba het volgende:
[..]
Oké.
Had je nog naar m'n profielwerkstuk gekeken?
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.


Waarschijnlijk is het gezien de hint de bedoeling dat je gebruik maakt van de middelwaardestelling. Deze zegt dat als een functie f: [a,b] → R continu is op [a,b] en differentieerbaar op (a,b), dat er dan een c ∈ (a,b) bestaat zodanig datquote:Op maandag 22 juli 2013 23:49 schreef Amoeba het volgende:
Opgave 4
Laat zien dat voor alle x > 0 geldt dat sin(x) < x.
Hint: sin(x) = sin(x) - sin(0)
sin(x) heeft een maximum van 1 (voor x = 1/2 π)
Dus als ik aan kan tonen dat x > sin(x) voor x (0,1] dan heb ik in feite de opgave aangetoond. Nu wil ik dit aantonen dmv de differentiaalrekening.
f(b) − f(a) = (b − a)·f'(c).
Aangezien d(sin(x))/dx = cos(x) en 0 < cos(x) < 1 voor 0 < x < π/2 volgt dan direct sin(x) − sin(0) < (x − 0) ofwel sin(x) < x voor 0 < x < π/2, en aangezien π/2 > 1 ben je dan klaar.
Echter, om analytisch aan te tonen dat d(sin(x))/dx = cos(x) moet je gebruik maken van limθ→0 sin(θ)/θ = 1. Maar om deze limiet aan te tonen moet je eerst aantonen dat sin(θ) < θ < tan(θ) voor 0 < θ < π/2 waaruit weer volgt dat cos(θ) < sin(θ)/θ < 1 voor 0 < | θ | < π/2 zodat met behulp van de insluitstelling én de continuïteit van de cosinusfunctie in θ = 0 volgt dat limθ→0 sin(θ)/θ = 1. Als de goniometrische functies meetkundig zijn gedefinieerd aan de hand van de eenheidscirkel, dan ontkom je niet aan een meetkundige beschouwing om aan te tonen dat sin(θ) < θ < tan(θ) voor 0 < θ < π/2, zodat je in een cirkelredenatie vervalt (no pun intended) als je dan d(sin(x))/dx = cos(x) weer gaat gebruiken om met behulp van de middelwaardestelling aan te tonen dat sin(x) < x voor x > 0.


Ik heb er iets van geprobeerd te breien zonder de definitie van limieten of Rieman integralen te gebruiken.quote:Op dinsdag 23 juli 2013 01:05 schreef Amoeba het volgende:
[..]
Daarom post ik het ook hier. Verder dan dit kom ik met het vwo niet, althans, niet met het gebruik van de differentiaalrekening.
Zou je me het ontbrekende deel uit kunnen leggen?
We willen aantonen dat sin(x)<x op (0, pi/2]. Oftewel x-sin(x)>0. Definieer f(x)=x-sin(x). We willen dus laten zien dat f(x)>0 voor x in (0,pi/2].
Merk op dat f(0)=0 en voor x in (0, pi/2] geldt f'(x)>0 . Voor x in (0,pi] geldt dus
De laatste stap volgt uit het feit dat f' continu is, en daarom de extreme value theorem gebruikt mag worden (http://en.wikipedia.org/wiki/Extreme_value_theorem). (Denk daar eens goed over na


De MAA site is niet down, maar helaas is deze site enkele dagen geleden zo maar zonder aankondiging gereorganiseerd, waardoor de oude URLs niet meer werken. En stom genoeg heeft men niet voorzien in redirects van de oude naar de nieuwe URLs, zodat veel 'oude' interne links nu ook niet meer werken. Hierdoor is het lastig materiaal terug te vinden. Ik kan de Putnam opgaven en uitwerkingen momenteel dan ook niet terugvinden, maar gelukkig hebben we voor dit soort eventualiteiten nog archive.org:quote:Op maandag 22 juli 2013 15:46 schreef randomo het volgende:
[..]
Boh, site is down. Het zijn nog best leuke problemen, ik heb er van de problemen van 2000 redelijk wat gemaakt, maar ik weet niet hoeveel ik er goed heb
http://web.archive.org/we(...)ms/putnamindex.shtml


Je had beter meteen even de bron van je opgave kunnen geven. Hieruit blijkt inderdaad dat het de bedoeling is dat je gebruik maakt van de middelwaardestelling.quote:Op dinsdag 23 juli 2013 00:44 schreef Amoeba het volgende:
[..]
Ik had ergens een vel met wat vragen gevonden en was uit pure verveling maar begonnen met het oplossen van de vragen.
http://www.win.tue.nl/~fransm/onderwijs/2DL00/Inhoud.pdf
Als je je verveelt en nog wat uitdagingen zoekt heb ik er nog wel eentje voor je. De afgelopen tijd heb ik vrij vaak gewezen op het belang van het kennen van merkwaardige producten en het beheersen van technieken als ontbinden in factoren en kwadraatafsplitsen in verband met het oplossen van vierkantsvergelijkingen. Deze technieken zijn natuurlijk gesneden koek voor iedereen die een beetje schoolalgebra kent, en de volgende opgaven zouden dan ook een eitje moeten zijn. Of toch niet?
Opgave 1. Ontbind a6 + b6 zo ver mogelijk in veeltermen in a en b met uitsluitend reële coëfficiënten.
Opgave 2. Idem voor a5 + b5.
Deze opgaven zijn oplosbaar met elementaire algebraïsche methoden, maar WolframAlpha en Google zullen je niet helpen (anders zou de aardigheid er snel af zijn) dus laat je kunsten maar eens zien ...


Nee natuurlijk niet, jou kennende zit ik weer tot middernacht te piekeren hoe ik dit op ga lossen.quote:Op dinsdag 23 juli 2013 02:26 schreef Riparius het volgende:
[..]
Je had beter meteen even de bron van je opgave kunnen geven. Hieruit blijkt inderdaad dat het de bedoeling is dat je gebruik maakt van de middelwaardestelling.
Als je je verveelt en nog wat uitdagingen zoekt heb ik er nog wel eentje voor je. De afgelopen tijd heb ik vrij vaak gewezen op het belang van het kennen van merkwaardige producten en het beheersen van technieken als ontbinden in factoren en kwadraatafsplitsen in verband met het oplossen van vierkantsvergelijkingen. Deze technieken zijn natuurlijk gesneden koek voor iedereen die een beetje schoolalgebra kent, en de volgende opgaven zouden dan ook een eitje moeten zijn. Of toch niet?
Opgave 1. Ontbind a6 + b6 zo ver mogelijk in veeltermen in a en b met uitsluitend reële coëfficiënten.
Opgave 2. Idem voor a5 + b5.
Deze opgaven zijn oplosbaar met elementaire algebraïsche methoden, maar WolframAlpha en Google zullen je niet helpen (anders zou de aardigheid er snel af zijn) dus laat je kunsten maar eens zien ...
Ik heb inderdaad gezien dat het onderwerp van de dag tot een paar dagen geleden ontbinden in factoren was, maar toen heb ik er niet veel aandacht aan besteed. Tijd om wat materiaal op te rakelen dus. Ik heb namelijk nog geen idee hoe ik dit aan moet pakken.


Je bent een heldquote:Op dinsdag 23 juli 2013 02:00 schreef Riparius het volgende:
[..]
De MAA site is niet down, maar helaas is deze site enkele dagen geleden zo maar zonder aankondiging gereorganiseerd, waardoor de oude URLs niet meer werken. En stom genoeg heeft men niet voorzien in redirects van de oude naar de nieuwe URLs, zodat veel 'oude' interne links nu ook niet meer werken. Hierdoor is het lastig materiaal terug te vinden. Ik kan de Putnam opgaven en uitwerkingen momenteel dan ook niet terugvinden, maar gelukkig hebben we voor dit soort eventualiteiten nog archive.org:
http://web.archive.org/we(...)ms/putnamindex.shtml
Ik had al eens gekeken op de 'wayback machine', toen kon ik het niet vinden. Ik zal wel niet goed gekeken hebben


Ik zat laatst eens na te denken over mijn fiets (mountainbike). Ik zit te denken om andere velgen te kopen, maar ik twijfel hoeveel effect dat heeft. Het voordeel is vooral afhankelijk van de velgsnelheid.
Als je naar 1 punt op de velg kijkt dan zie je dat dat punt een absolute sinus functie beschrijft tijdens het rijden
Maar wat is dan de snelheid van dat punt? (de afgeleide/snelheid van normale sinus is cos..) Dus ik vroeg me af of een (absolute) cosinus ook de snelheid beschrift van een absolute sinusfunctie. En wat de velgsnelheid is tov van de rijsnelheid.
Ik hoop dat mijn verhaal duidelijk is en dat iemand mij dit toe kan lichten.
Edit, mijn boerenverstand zegt dat het punt bovenaan 2x de rijsnelheid heeft, maar ik kan dit niet theoretisch bewijzen.
[ Bericht 7% gewijzigd door the85mc op 23-07-2013 13:11:33 ]
Als je naar 1 punt op de velg kijkt dan zie je dat dat punt een absolute sinus functie beschrijft tijdens het rijden
Maar wat is dan de snelheid van dat punt? (de afgeleide/snelheid van normale sinus is cos..) Dus ik vroeg me af of een (absolute) cosinus ook de snelheid beschrift van een absolute sinusfunctie. En wat de velgsnelheid is tov van de rijsnelheid.
Ik hoop dat mijn verhaal duidelijk is en dat iemand mij dit toe kan lichten.
Edit, mijn boerenverstand zegt dat het punt bovenaan 2x de rijsnelheid heeft, maar ik kan dit niet theoretisch bewijzen.
[ Bericht 7% gewijzigd door the85mc op 23-07-2013 13:11:33 ]


Per meter die je band rolt ga je toch gewoon 1 meter vooruit? Dus je snelheid en die van de band moeten gelijk zijn.quote:Op dinsdag 23 juli 2013 13:04 schreef the85mc het volgende:
Ik zat laatst eens na te denken over mijn fiets (mountainbike). Ik zit te denken om andere velgen te kopen, maar ik twijfel hoeveel effect dat heeft. Het voordeel is vooral afhankelijk van de velgsnelheid.
Als je naar 1 punt op de velg kijkt dan zie je dat dat punt een absolute sinus functie maakt.
Maar wat is dan de snelheid, (de afgeleide van normale sinus is cos..) Dus ik vroeg me af of een cosinus ook de.snelheid beschrift van een absolute sinusfunctie. En wat de velgsnelheid is tov van de rijsnelheid.
Ik hoop dat mijn verhaal duidelijk is en dat iemand mij dit toe kan lichten.
Edit, mijn boerenverstand zegt dat het punt bovenaan 2x de rijsnelheid heeft, maar ik kan dit niet theoretisch bewijzen.
Een sinosoïde geeft slechts de "hoogte" van een punt op je band na verloop van tijd. De afgeleide daarvan is dus de component van de snelheid in de y-richting, van een bepaald punt op de band.


De as rolt inderdaad 1 meter vooruit. Masr de velg beschrijft dus een sinus functie. Dan zou je zeggen dat de snelheid tov de lucht (dus niet de weg) niet constant is.quote:Op dinsdag 23 juli 2013 13:12 schreef thenxero het volgende:
[..]
Per meter die je band rolt ga je toch gewoon 1 meter vooruit? Dus je snelheid en die van de band moeten gelijk zijn.


De angularvelocity is overal in je velg hetzelfde.quote:Op dinsdag 23 juli 2013 13:04 schreef the85mc het volgende:
Ik zat laatst eens na te denken over mijn fiets (mountainbike). Ik zit te denken om andere velgen te kopen, maar ik twijfel hoeveel effect dat heeft. Het voordeel is vooral afhankelijk van de velgsnelheid.
Als je naar 1 punt op de velg kijkt dan zie je dat dat punt een absolute sinus functie beschrijft tijdens het rijden
Maar wat is dan de snelheid van dat punt? (de afgeleide/snelheid van normale sinus is cos..) Dus ik vroeg me af of een (absolute) cosinus ook de snelheid beschrift van een absolute sinusfunctie. En wat de velgsnelheid is tov van de rijsnelheid.
Ik hoop dat mijn verhaal duidelijk is en dat iemand mij dit toe kan lichten.
Edit, mijn boerenverstand zegt dat het punt bovenaan 2x de rijsnelheid heeft, maar ik kan dit niet theoretisch bewijzen.
Afhankelijk van de afstand tot het midden is er een bepaalde snelheid im een punt.
Het punt boven of beneden heeft dezelfde snelheid. Waarom zou bovenin de snelheid 2 keer zo groot zijn?


Jawel. Stel dat je een punt markeert op je band en dat de straal 1 (meter) is. Laten we zeggen dat we de rechterkant van de band ter hoogte van de as markeren. Als de band dan naar links gaat rijden, dan volgt de hoogte van het punt op de band (ten opzichte van de as) een sinusgrafiek. De zijwaartse afwijking kan je beschrijven met een cosinus (een afwijking naar rechts kiezen we als positief).quote:Op dinsdag 23 juli 2013 13:15 schreef the85mc het volgende:
[..]
De as rolt inderdaad 1 meter vooruit. Masr de velg beschrijft dus een sinus functie. Dan zou je zeggen dat de snelheid tov de lucht (dus niet de weg) niet constant is.
De snelheid van het punt op je band is nu de vector die wordt opgespannen door de x en y component. Met de stelling van Pythagoras krijg je dan dat de lengte van deze somvector gelijk is aan cos²(t) + sin²(t) = 1. De grootte snelheid is dus constant (maar de richting verandert uiteraard).
Maar dit kan je natuurlijk ook op je klompen al aanvoelen. Als een stuk van je velg sneller zou gaan dan een ander stuk, schuift het dan in elkaar?


Ja het klopt dat rad/s constant is bij constante snelheid. Maar wat is dan de snelheid tov de x as? Die is niet constant.
Dat kan namelijk niet: de as beweegt met constante snelheid over de x as. 1 punt op de velg is het ene moment achter de as en later voor de as. Dan moet ie ergens sneller gaan dan de as snelheid.
Dat kan namelijk niet: de as beweegt met constante snelheid over de x as. 1 punt op de velg is het ene moment achter de as en later voor de as. Dan moet ie ergens sneller gaan dan de as snelheid.


Ter verduidelijking, het gaat niet om hoeksnelheid, maar snelheid tov de x as.
Wat we eigenlijk nodig hebben is een fiets en een stroboscoop
Wat we eigenlijk nodig hebben is een fiets en een stroboscoop


Oh zo.quote:Op dinsdag 23 juli 2013 13:32 schreef the85mc het volgende:
Ter verduidelijking, het gaat niet om hoeksnelheid, maar snelheid tov de x as.
Wat we eigenlijk nodig hebben is een fiets en een stroboscoop
Nou schrijf eerst eens de beweging op in referenceframe van middelpunt wiel en dan vanuit de weg.
Moet nit zo moeilik zijn toch?
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |




 Op
Op 


