SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Je moet maar opzoeken hoeveel geld een theoretische wiskundige verdient voor het aantal uren dat hij van zijn leven erin stopt.quote:Op woensdag 17 juli 2013 19:37 schreef Amoeba het volgende:
[..]
Zo'n havist had last minute 10 uur werk erin gestoken en ontvangt een 9. Ik heb hier tantoe hard voor na zitten denken en krijg een 7. Het leven is een partij oneerlijk.
Hoe theoretischer een wiskundige is, hoe harder hij genaaid wordt.
Ik wil trouwens best je pws lezen, want nu ben ik wel benieuwd.
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
De opgave is duidelijk, dat je met de discriminant moet werken ook. Maar waar halen ze die derde vergelijking vandaan? Het is namelijk geen herleiding, want als je ze plot krijgt je twee andere grafieken.
Gist is liefde, gist is leven. Vooral in een vagijn.
Beide kanten vermenigvuldigen met 2x+a.quote:Op donderdag 18 juli 2013 20:03 schreef Rezania het volgende:
[ afbeelding ]
[ afbeelding ]
De opgave is duidelijk, dat je met de discriminant moet werken ook. Maar waar halen ze die derde vergelijking vandaan? Het is namelijk geen herleiding, want als je ze plot krijgt je twee andere grafieken.
Ohh, zo.quote:
[..]
Beide kanten vermenigvuldigen met 2x+a.
Bedankt.
Gist is liefde, gist is leven. Vooral in een vagijn.
Nog een vraagje. (Sorry, het is allemaal een beetje weggezakt de laatste tijd. )
Ik wil een breuk primitiveren;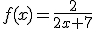
Dan krijg je sowieso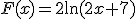
, maar ik heb het idee dat dit nog niet compleet is. Ik heb heel sterk de neiging om te concluderen dat je nog wat met die 
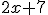moet doen, maar wat ook al weer?
)Ik wil een breuk primitiveren;
Dan krijg je sowieso
Gist is liefde, gist is leven. Vooral in een vagijn.
Je zit in de buurt. Als je de "primitieve" differentieert (met kettingregel!) dan zie je dat je niet de originele functie terugkrijgt: je zit er een constante naast.quote:
Nog een vraagje. (Sorry, het is allemaal een beetje weggezakt de laatste tijd.
Ik wil een breuk primitiveren;
Dan krijg je sowieso
Ah ja, differentiëren om de primitieve te controleren, dat is wel handig.quote:
[..]
Je zit in de buurt. Als je de "primitieve" differentieert (met kettingregel!) dan zie je dat je niet de originele functie terugkrijgt: je zit er een constante naast.
Dat ga ik dan even doen, nogmaals bedankt.
Gist is liefde, gist is leven. Vooral in een vagijn.
Ik ben mijn USB stick met het origineel kwijtgeraaktquote:
[..]
Je moet maar opzoeken hoeveel geld een theoretische wiskundige verdient voor het aantal uren dat hij van zijn leven erin stopt.
Hoe theoretischer een wiskundige is, hoe harder hij genaaid wordt.
Ik wil trouwens best je pws lezen, want nu ben ik wel benieuwd.
Dit is een van de laatste versies. Er kan dus nog ergens een typo ofzo instaan, maar het geeft een idee.
Je hebt DM.. Mijn naam en toenaam staan erbij namelijk.
Het enige wat je fout deed was die vermenigvuldiging met 2 ervoor zetten. Differentïeren van ln(2x+7) met de kettingregel geeft 1/(2x+7) * [2x+7]' = 1/(2x+7) * 2 = 2/(2x+7)quote:
Je kon dit direct zien doordat 2 de afgeleide is van 2x+7. Dat je dat direct herkent, daar willen ze uiteindelijk naartoe.
Ja, dat had ik me ook al bedacht.quote:
[..]
Het enige wat je fout deed was die vermenigvuldiging met 2 ervoor zetten. Differentïeren van ln(2x+7) met de kettingregel geeft 1/(2x+7) * [2x+7]' = 1/(2x+7) * 2 = 2/(2x+7)
Je kon dit direct zien doordat 2 de afgeleide is van 2x+7. Dat je dat direct herkent, daar willen ze uiteindelijk naartoe.
Het was alleen even weggezakt, maar nu moet de rest wel lukken (qua integreren dan).
Gist is liefde, gist is leven. Vooral in een vagijn.
[ Bericht 100% gewijzigd door Bram_van_Loon op 19-07-2013 14:00:23 ]
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Ik ben weer ergens op vastgelopen, gonio deze keer.
Hoe komen zij aan
?
Hoe komen zij aan
Gist is liefde, gist is leven. Vooral in een vagijn.
Bedoel je die bijna laatste gelijkheid?quote:
Ik ben weer ergens op vastgelopen, gonio deze keer.
[ afbeelding ]
[ afbeelding ]
Hoe komen zij aan
Daar kun je 0,5*cos(x)*(3 + sin(2x)) namelijk uitschrijven (dus zonder de haakjes om 3 + sin(2x)) en dan kun je zien dat er wat weg valt. Vervolgens kun je er weer haakjes omheen bouwen.
Oh, gewoon herleiden en dan ontbinden in factoren dus? Ik dacht dat het iets met de goniometrieregels had te maken.quote:
[..]
Bedoel je die bijna laatste gelijkheid?
Daar kun je 0,5*cos(x)*(3 + sin(2x)) namelijk uitschrijven (dus zonder de haakjes om 3 + sin(2x)) en dan kun je zien dat er wat weg valt. Vervolgens kun je er weer haakjes omheen bouwen.
Bedankt.
Gist is liefde, gist is leven. Vooral in een vagijn.
Even een vraagje over verzamelingenleer. Klopt het dat het supremum niets anders is dan de grootste bovengrens en het infinum de kleinste ondergrens?
Bijna goedquote:
Even een vraagje over verzamelingenleer. Klopt het dat het supremum niets anders is dan de grootste bovengrens en het infinum de kleinste ondergrens?
, het supremum is de kleinste bovengrens en infimum is de grootste ondergrens.
Dus bijvoorbeeld, [0,1) heeft geen maximum. (Want stel er is een maximum x. Dan geldt x < x+(1-x)/2 <1, tegenspraak.) Maar het supremum is 1. In dit geval is het infumum en het minimum 0.quote:
[..]
Bijna goed
Zo voelde ik me ook. Ik heb uiteindelijk een wiskundig getint PWS ingeleverd, maar het werd nagekeken door een biologiedocent, en die hield niet van wiskundequote:
Gelukkig uiteindelijk nog wel een 8 gekregen, maar ik hoorde van mensen dat ze in één dag een PWS in elkaar geflanst hebben en ook een 8 hadden.
Wolfram Alpha derpt soms, heb ik ook weleens last van gehad. Ik denk dat je browser opnieuw opstarten kan helpen. Ik kan me voorstellen dat ze verschillende servers hebben met verschillende versies software, en dat het daardoor komt.quote:[..]
Nu snap ik er ook niks meer van. Net kon hij er niet veel van maken.
Mensen die beweren er 1 dag aan gewerkt te hebben zijn van die nerdjes die stiekem al 2 jaar bezig zijn met voorbereiden.
Dan hebben ze het gewoon met flink wat knip- en plakwerk bij elkaar gesprokkeld vanaf internet. Een beetje docent ziet dat meteen, alleen al door de wisselende schrijfstijlen of het inconsequente gebruik van notaties of een gebrekkige opbouw van het geheel, maar waarschijnlijk zijn er ook veel docenten die de kantjes eraf lopen en het wel best vinden, of geen zin hebben zich erin te verdiepen omdat het buiten hun eigenlijke vakgebied ligt, en dan krijg je dit soort 'beoordelingen'.quote:
[..]
Gelukkig uiteindelijk nog wel een 8 gekregen, maar ik hoorde van mensen dat ze in één dag een PWS in elkaar geflanst hebben en ook een 8 hadden.
Ik denk het niet, heb er geen last van. WolframAlpha gebruikt inderdaad verschillende servers, maar ik heb nooit verschillen bemerkt. Wel is er het probleem dat de eerste paar karakters die je typt vaak niet doorkomen als je de hoofdpagina van WolframAlpha oproept en direct iets invoert. Als je dan niet oplet wat je precies invoert dan kan het inderdaad gemakkelijk gebeuren dat WolframAlpha de syntaxis niet begrijpt of verkeerd interpreteert.quote:[..]
Wolfram Alpha derpt soms, heb ik ook weleens last van gehad. Ik denk dat je browser opnieuw opstarten kan helpen. Ik kan me voorstellen dat ze verschillende servers hebben met verschillende versies software, en dat het daardoor komt.
Ja dat bedoelde ik, schreef het alleen verkeerd op. Bedankt in ieder geval.quote:
[..]
Bijna goed
Ja, afhankelijk van of de grenzen ook in de verzameling zitten zit het supremum/infinum dus wel/niet zelf in de verzameling. Bedankt voor de reactie.quote:
[..]
Dus bijvoorbeeld, [0,1) heeft geen maximum. (Want stel er is een maximum x. Dan geldt x < x+(1-x)/2 <1, tegenspraak.) Maar het supremum is 1. In dit geval is het infumum en het minimum 0.
Ik heb het maar één keer gehad (maar ik heb wolfram best vaak gebruikt), maar ik weet wel zeker dat ik het toen niet verkeerd heb ingetypt (ik had het toen van een link). Maargoed, voor hetzelfde geld ging er iets anders fout op de server, daar valt verder niet zoveel over te zeggen.quote:
Ik denk het niet, heb er geen last van. WolframAlpha gebruikt inderdaad verschillende servers, maar ik heb nooit verschillen bemerkt. Wel is er het probleem dat de eerste paar karakters die je typt vaak niet doorkomen als je de hoofdpagina van WolframAlpha oproept en direct iets invoert. Als je dan niet oplet wat je precies invoert dan kan het inderdaad gemakkelijk gebeuren dat WolframAlpha de syntaxis niet begrijpt of verkeerd interpreteert.
Boh, site is down. Het zijn nog best leuke problemen, ik heb er van de problemen van 2000 redelijk wat gemaakt, maar ik weet niet hoeveel ik er goed hebquote:
[...]
Oh, laat maar. Ik ben net deze site tegengekomen. De makkelijkste daarvan zijn denk ik wel een goede uitdaging
Voor mijn PWS op de havo was ik maar 8 uurtjes bezig. Op de vwo was het een ander verhaal.quote:
Mensen die beweren er 1 dag aan gewerkt te hebben zijn van die nerdjes die stiekem al 2 jaar bezig zijn met voorbereiden.
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Opgave 4
Laat zien dat voor alle x > 0 geldt dat sin(x) < x.
Hint: sin(x) = sin(x) - sin(0)
sin(x) heeft een maximum van 1 (voor x = 1/2 π)
Dus als ik aan kan tonen dat x > sin(x) voor x (0,1] dan heb ik in feite de opgave aangetoond. Nu wil ik dit aantonen dmv de differentiaalrekening. Als ik kan aantonen dat d(sin(x))/dx op het interval (0,1] nooit groter is dan 1 is dit toch gelukt? Immers, x stijgt constant met een richtingscoëfficient van 1.
dus:
d(sin(x))/dx = cos(x)
cos(x) = 1
x = 0 ^ x = 2π
Zouden ze dit op een tentamen pikken?
[ Bericht 0% gewijzigd door #ANONIEM op 22-07-2013 23:50:44 ]
Laat zien dat voor alle x > 0 geldt dat sin(x) < x.
Hint: sin(x) = sin(x) - sin(0)
sin(x) heeft een maximum van 1 (voor x = 1/2 π)
Dus als ik aan kan tonen dat x > sin(x) voor x (0,1] dan heb ik in feite de opgave aangetoond. Nu wil ik dit aantonen dmv de differentiaalrekening. Als ik kan aantonen dat d(sin(x))/dx op het interval (0,1] nooit groter is dan 1 is dit toch gelukt? Immers, x stijgt constant met een richtingscoëfficient van 1.
dus:
d(sin(x))/dx = cos(x)
cos(x) = 1
x = 0 ^ x = 2π
Zouden ze dit op een tentamen pikken?
[ Bericht 0% gewijzigd door #ANONIEM op 22-07-2013 23:50:44 ]
Je hebt het denk ik over het interval (0, pi/2]. Ik weet niet of ze dit pikken. Wat namelijk nog wel een beetje sneaky is, is dat in het punt 0 de afgeleides hetzelfde zijn. Dus misschien is er nog een punt x>0 ("heeeel dicht bij 0") zodat sin(x)=x. Dat mag niet, want je moet strikte ongelijkheid aantonen. Daar zou je dan nog wat voor moeten bedenken... als je het echt netjes wil doen.quote:
Opgave 4
Laat zien dat voor alle x > 0 geldt dat sin(x) < x.
Hint: sin(x) = sin(x) - sin(0)
sin(x) heeft een maximum van 1 (voor x = 1/2 π)
Dus als ik aan kan tonen dat x > sin(x) voor x (0,1] dan heb ik in feite de opgave aangetoond. Nu wil ik dit aantonen dmv de differentiaalrekening. Als ik kan aantonen dat d(sin(x))/dx op het interval (0,1] nooit groter is dan 1 is dit toch gelukt? Immers, x stijgt constant met een richtingscoëfficient van 1.
dus:
d(sin(x))/dx = cos(x)
cos(x) = 1
x = 0 ^ x = 2π
Zouden ze dit op een tentamen pikken?
Voor welke vak is dit? Je moet overigens aantonen dat de afgeleide op het interval (0,pi/2] strikt kleiner is dan één. Dan is het goed. Je kunt het netjes maken met Riemann integratie of met de limietdefinitie van afgeleiden, de tweede is makkelijker.quote:
Opgave 4
Laat zien dat voor alle x > 0 geldt dat sin(x) < x.
Hint: sin(x) = sin(x) - sin(0)
sin(x) heeft een maximum van 1 (voor x = 1/2 π)
Dus als ik aan kan tonen dat x > sin(x) voor x (0,1] dan heb ik in feite de opgave aangetoond. Nu wil ik dit aantonen dmv de differentiaalrekening. Als ik kan aantonen dat d(sin(x))/dx op het interval (0,1] nooit groter is dan 1 is dit toch gelukt? Immers, x stijgt constant met een richtingscoëfficient van 1.
dus:
d(sin(x))/dx = cos(x)
cos(x) = 1
x = 0 ^ x = 2π
Zouden ze dit op een tentamen pikken?
[ Bericht 2% gewijzigd door Mathemaat op 23-07-2013 00:30:36 ]
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Het punt 0 heeft niets van doen met de hele vraag, daar het punt 0 buiten het gevraagde interval valt.quote:
[..]
Je hebt het denk ik over het interval (0, pi/2]. Ik weet niet of ze dit pikken. Wat namelijk nog wel een beetje sneaky is, is dat in het punt 0 de afgeleides hetzelfde zijn. Dus misschien is er nog een punt x>0 ("heeeel dicht bij 0") zodat sin(x)=x. Dat mag niet, want je moet strikte ongelijkheid aantonen. Daar zou je dan nog wat voor moeten bedenken... als je het echt netjes wil doen.
http://fooplot.com/plot/oqbbqj2gop
Hier kun je zien wat ik bedoel. Ik zeg dat voor iedere x > 1 het evident is dat sin(x) < x, want sin(x) heeft een maximum van 1.
Dus als aan kan tonen dat op het interval (0, 1] geldt dat sin(x) nooit meer toeneemt dan y = x (met rc = 1 ), dan heb ik toch aangetoond dat sin(x) < x voor x (0, 1]? Immers, sin(x) = x voor x = 0 want dan sin(x) = 0.
y = x neemt constant toe. Als ik aantoon dat sin(x) nooit meer toeneemt op het interval (0,1] dan y = x ben ik toch klaar?quote:Dus misschien is er nog een punt x>0 ("heeeel dicht bij 0") zodat sin(x)=x. Dat mag niet, want je moet strikte ongelijkheid aantonen.
[ Bericht 7% gewijzigd door #ANONIEM op 23-07-2013 00:52:13 ]
Weet ik veel, calculus ofzo. Ik had ergens een vel met wat vragen gevonden en was uit pure verveling maar begonnen met het oplossen van de vragen.quote:
[..]
Voor welke vak is dit? Je moet overigens aantonen dat de afgeleide op het interval (0,pi/2] strikt kleiner is dan één. Dan is het goed. Je kunt het netjes maken met Riemann integratie of met de limietdefinitie van afgeleiden, de tweede is makkelijker.
http://www.win.tue.nl/~fransm/onderwijs/2DL00/Inhoud.pdf
[ Bericht 8% gewijzigd door #ANONIEM op 23-07-2013 00:46:55 ]
Ik begrijp je wel, maar jij begrijpt mij niet. En het feit dat je er zelf nog je vraagtekens bij zet, suggereert al dat het niet een 100% rigoreus bewijs is. Aangezien calculus vaak niet 100% rigoreus is zal het daar wel voldoen. Bij een analysevak krijg je er geen punten voor.quote:
[..]
Het punt 0 heeft niets van doen met de hele vraag, daar het punt 0 buiten het gevraagde interval valt.
http://fooplot.com/plot/oqbbqj2gop
Hier kun je zien wat ik bedoel. Ik zeg dat voor iedere x > 1 het evident is dat sin(x) < x, want sin(x) heeft een maximum van 1.
Dus als aan kan tonen dat op het interval (0, 1] geldt dat sin(x) nooit meer toeneemt dan y = x (met rc = 1 ), dan heb ik toch aangetoond dat sin(x) < x voor x (0, 1]? Immers, sin(x) = x voor x = 0 want dan sin(x) = 0.
[..]
y = x neemt constant toe. Als ik aantoon dat sin(x) nooit meer toeneemt op het interval (0,1] dan y = x ben ik toch klaar?
Daarom post ik het ook hier. Verder dan dit kom ik met het vwo niet, althans, niet met het gebruik van de differentiaalrekening.quote:
[..]
Ik begrijp je wel, maar jij begrijpt mij niet. En het feit dat je er zelf nog je vraagtekens bij zet, suggereert al dat het niet een 100% rigoreus bewijs is. Aangezien calculus vaak niet 100% rigoreus is zal het daar wel voldoen. Bij een analysevak krijg je er geen punten voor.
Zou je me het ontbrekende deel uit kunnen leggen?
Bij de analysevakken krijg je netjes geleerd hoe netjes dingen op moet schrijven. Dat kun je niet even uitleggen.quote:
[..]
Daarom post ik het ook hier. Verder dan dit kom ik met het vwo niet, althans, niet met het gebruik van de differentiaalrekening.
Zou je me het ontbrekende deel uit kunnen leggen?
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Oké.quote:
[..]
Bij de analysevakken krijg je netjes geleerd hoe netjes dingen op moet schrijven. Dat kun je niet even uitleggen.
Had je nog naar m'n profielwerkstuk gekeken?
Ja, het zag er idd interessant uit. Maar ik heb niet zoveel verstand van profielwerkstukken, dus ik kan er niet zoveel over zeggen .quote:
[..]
Oké.
Had je nog naar m'n profielwerkstuk gekeken?
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Waarschijnlijk is het gezien de hint de bedoeling dat je gebruik maakt van de middelwaardestelling. Deze zegt dat als een functie f: [a,b] → R continu is op [a,b] en differentieerbaar op (a,b), dat er dan een c ∈ (a,b) bestaat zodanig datquote:
Opgave 4
Laat zien dat voor alle x > 0 geldt dat sin(x) < x.
Hint: sin(x) = sin(x) - sin(0)
sin(x) heeft een maximum van 1 (voor x = 1/2 π)
Dus als ik aan kan tonen dat x > sin(x) voor x (0,1] dan heb ik in feite de opgave aangetoond. Nu wil ik dit aantonen dmv de differentiaalrekening.
f(b) − f(a) = (b − a)·f'(c).
Aangezien d(sin(x))/dx = cos(x) en 0 < cos(x) < 1 voor 0 < x < π/2 volgt dan direct sin(x) − sin(0) < (x − 0) ofwel sin(x) < x voor 0 < x < π/2, en aangezien π/2 > 1 ben je dan klaar.
Echter, om analytisch aan te tonen dat d(sin(x))/dx = cos(x) moet je gebruik maken van limθ→0 sin(θ)/θ = 1. Maar om deze limiet aan te tonen moet je eerst aantonen dat sin(θ) < θ < tan(θ) voor 0 < θ < π/2 waaruit weer volgt dat cos(θ) < sin(θ)/θ < 1 voor 0 < | θ | < π/2 zodat met behulp van de insluitstelling én de continuïteit van de cosinusfunctie in θ = 0 volgt dat limθ→0 sin(θ)/θ = 1. Als de goniometrische functies meetkundig zijn gedefinieerd aan de hand van de eenheidscirkel, dan ontkom je niet aan een meetkundige beschouwing om aan te tonen dat sin(θ) < θ < tan(θ) voor 0 < θ < π/2, zodat je in een cirkelredenatie vervalt (no pun intended) als je dan d(sin(x))/dx = cos(x) weer gaat gebruiken om met behulp van de middelwaardestelling aan te tonen dat sin(x) < x voor x > 0.
Ik heb er iets van geprobeerd te breien zonder de definitie van limieten of Rieman integralen te gebruiken.quote:
[..]
Daarom post ik het ook hier. Verder dan dit kom ik met het vwo niet, althans, niet met het gebruik van de differentiaalrekening.
Zou je me het ontbrekende deel uit kunnen leggen?
We willen aantonen dat sin(x)<x op (0, pi/2]. Oftewel x-sin(x)>0. Definieer f(x)=x-sin(x). We willen dus laten zien dat f(x)>0 voor x in (0,pi/2].
Merk op dat f(0)=0 en voor x in (0, pi/2] geldt f'(x)>0 . Voor x in (0,pi] geldt dus
De laatste stap volgt uit het feit dat f' continu is, en daarom de extreme value theorem gebruikt mag worden (http://en.wikipedia.org/wiki/Extreme_value_theorem). (Denk daar eens goed over na
)
De MAA site is niet down, maar helaas is deze site enkele dagen geleden zo maar zonder aankondiging gereorganiseerd, waardoor de oude URLs niet meer werken. En stom genoeg heeft men niet voorzien in redirects van de oude naar de nieuwe URLs, zodat veel 'oude' interne links nu ook niet meer werken. Hierdoor is het lastig materiaal terug te vinden. Ik kan de Putnam opgaven en uitwerkingen momenteel dan ook niet terugvinden, maar gelukkig hebben we voor dit soort eventualiteiten nog archive.org:quote:
[..]
Boh, site is down. Het zijn nog best leuke problemen, ik heb er van de problemen van 2000 redelijk wat gemaakt, maar ik weet niet hoeveel ik er goed heb
http://web.archive.org/we(...)ms/putnamindex.shtml
Je had beter meteen even de bron van je opgave kunnen geven. Hieruit blijkt inderdaad dat het de bedoeling is dat je gebruik maakt van de middelwaardestelling.quote:
[..]
Ik had ergens een vel met wat vragen gevonden en was uit pure verveling maar begonnen met het oplossen van de vragen.
http://www.win.tue.nl/~fransm/onderwijs/2DL00/Inhoud.pdf
Als je je verveelt en nog wat uitdagingen zoekt heb ik er nog wel eentje voor je. De afgelopen tijd heb ik vrij vaak gewezen op het belang van het kennen van merkwaardige producten en het beheersen van technieken als ontbinden in factoren en kwadraatafsplitsen in verband met het oplossen van vierkantsvergelijkingen. Deze technieken zijn natuurlijk gesneden koek voor iedereen die een beetje schoolalgebra kent, en de volgende opgaven zouden dan ook een eitje moeten zijn. Of toch niet?
Opgave 1. Ontbind a6 + b6 zo ver mogelijk in veeltermen in a en b met uitsluitend reële coëfficiënten.
Opgave 2. Idem voor a5 + b5.
Deze opgaven zijn oplosbaar met elementaire algebraïsche methoden, maar WolframAlpha en Google zullen je niet helpen (anders zou de aardigheid er snel af zijn) dus laat je kunsten maar eens zien ...
Nee natuurlijk niet, jou kennende zit ik weer tot middernacht te piekeren hoe ik dit op ga lossen.quote:
[..]
Je had beter meteen even de bron van je opgave kunnen geven. Hieruit blijkt inderdaad dat het de bedoeling is dat je gebruik maakt van de middelwaardestelling.
Als je je verveelt en nog wat uitdagingen zoekt heb ik er nog wel eentje voor je. De afgelopen tijd heb ik vrij vaak gewezen op het belang van het kennen van merkwaardige producten en het beheersen van technieken als ontbinden in factoren en kwadraatafsplitsen in verband met het oplossen van vierkantsvergelijkingen. Deze technieken zijn natuurlijk gesneden koek voor iedereen die een beetje schoolalgebra kent, en de volgende opgaven zouden dan ook een eitje moeten zijn. Of toch niet?
Opgave 1. Ontbind a6 + b6 zo ver mogelijk in veeltermen in a en b met uitsluitend reële coëfficiënten.
Opgave 2. Idem voor a5 + b5.
Deze opgaven zijn oplosbaar met elementaire algebraïsche methoden, maar WolframAlpha en Google zullen je niet helpen (anders zou de aardigheid er snel af zijn) dus laat je kunsten maar eens zien ...
Ik heb inderdaad gezien dat het onderwerp van de dag tot een paar dagen geleden ontbinden in factoren was, maar toen heb ik er niet veel aandacht aan besteed. Tijd om wat materiaal op te rakelen dus. Ik heb namelijk nog geen idee hoe ik dit aan moet pakken.
Je bent een heldquote:
[..]
De MAA site is niet down, maar helaas is deze site enkele dagen geleden zo maar zonder aankondiging gereorganiseerd, waardoor de oude URLs niet meer werken. En stom genoeg heeft men niet voorzien in redirects van de oude naar de nieuwe URLs, zodat veel 'oude' interne links nu ook niet meer werken. Hierdoor is het lastig materiaal terug te vinden. Ik kan de Putnam opgaven en uitwerkingen momenteel dan ook niet terugvinden, maar gelukkig hebben we voor dit soort eventualiteiten nog archive.org:
http://web.archive.org/we(...)ms/putnamindex.shtml
! Volgens mij hebben ze op de nieuwe/gereorganiseerde site de oude opgaven er (nog?) niet opstaan.Ik had al eens gekeken op de 'wayback machine', toen kon ik het niet vinden. Ik zal wel niet goed gekeken hebben
Ik zat laatst eens na te denken over mijn fiets (mountainbike). Ik zit te denken om andere velgen te kopen, maar ik twijfel hoeveel effect dat heeft. Het voordeel is vooral afhankelijk van de velgsnelheid.
Als je naar 1 punt op de velg kijkt dan zie je dat dat punt een absolute sinus functie beschrijft tijdens het rijden
Maar wat is dan de snelheid van dat punt? (de afgeleide/snelheid van normale sinus is cos..) Dus ik vroeg me af of een (absolute) cosinus ook de snelheid beschrift van een absolute sinusfunctie. En wat de velgsnelheid is tov van de rijsnelheid.
Ik hoop dat mijn verhaal duidelijk is en dat iemand mij dit toe kan lichten.
Edit, mijn boerenverstand zegt dat het punt bovenaan 2x de rijsnelheid heeft, maar ik kan dit niet theoretisch bewijzen.
[ Bericht 7% gewijzigd door the85mc op 23-07-2013 13:11:33 ]
Als je naar 1 punt op de velg kijkt dan zie je dat dat punt een absolute sinus functie beschrijft tijdens het rijden
Maar wat is dan de snelheid van dat punt? (de afgeleide/snelheid van normale sinus is cos..) Dus ik vroeg me af of een (absolute) cosinus ook de snelheid beschrift van een absolute sinusfunctie. En wat de velgsnelheid is tov van de rijsnelheid.
Ik hoop dat mijn verhaal duidelijk is en dat iemand mij dit toe kan lichten.
Edit, mijn boerenverstand zegt dat het punt bovenaan 2x de rijsnelheid heeft, maar ik kan dit niet theoretisch bewijzen.
[ Bericht 7% gewijzigd door the85mc op 23-07-2013 13:11:33 ]
Per meter die je band rolt ga je toch gewoon 1 meter vooruit? Dus je snelheid en die van de band moeten gelijk zijn.quote:Op dinsdag 23 juli 2013 13:04 schreef the85mc het volgende:
Ik zat laatst eens na te denken over mijn fiets (mountainbike). Ik zit te denken om andere velgen te kopen, maar ik twijfel hoeveel effect dat heeft. Het voordeel is vooral afhankelijk van de velgsnelheid.
Als je naar 1 punt op de velg kijkt dan zie je dat dat punt een absolute sinus functie maakt.
Maar wat is dan de snelheid, (de afgeleide van normale sinus is cos..) Dus ik vroeg me af of een cosinus ook de.snelheid beschrift van een absolute sinusfunctie. En wat de velgsnelheid is tov van de rijsnelheid.
Ik hoop dat mijn verhaal duidelijk is en dat iemand mij dit toe kan lichten.
Edit, mijn boerenverstand zegt dat het punt bovenaan 2x de rijsnelheid heeft, maar ik kan dit niet theoretisch bewijzen.
Een sinosoïde geeft slechts de "hoogte" van een punt op je band na verloop van tijd. De afgeleide daarvan is dus de component van de snelheid in de y-richting, van een bepaald punt op de band.
De as rolt inderdaad 1 meter vooruit. Masr de velg beschrijft dus een sinus functie. Dan zou je zeggen dat de snelheid tov de lucht (dus niet de weg) niet constant is.quote:
[..]
Per meter die je band rolt ga je toch gewoon 1 meter vooruit? Dus je snelheid en die van de band moeten gelijk zijn.
De angularvelocity is overal in je velg hetzelfde.quote:
Ik zat laatst eens na te denken over mijn fiets (mountainbike). Ik zit te denken om andere velgen te kopen, maar ik twijfel hoeveel effect dat heeft. Het voordeel is vooral afhankelijk van de velgsnelheid.
Als je naar 1 punt op de velg kijkt dan zie je dat dat punt een absolute sinus functie beschrijft tijdens het rijden
Maar wat is dan de snelheid van dat punt? (de afgeleide/snelheid van normale sinus is cos..) Dus ik vroeg me af of een (absolute) cosinus ook de snelheid beschrift van een absolute sinusfunctie. En wat de velgsnelheid is tov van de rijsnelheid.
Ik hoop dat mijn verhaal duidelijk is en dat iemand mij dit toe kan lichten.
Edit, mijn boerenverstand zegt dat het punt bovenaan 2x de rijsnelheid heeft, maar ik kan dit niet theoretisch bewijzen.
Afhankelijk van de afstand tot het midden is er een bepaalde snelheid im een punt.
Het punt boven of beneden heeft dezelfde snelheid. Waarom zou bovenin de snelheid 2 keer zo groot zijn?
Jawel. Stel dat je een punt markeert op je band en dat de straal 1 (meter) is. Laten we zeggen dat we de rechterkant van de band ter hoogte van de as markeren. Als de band dan naar links gaat rijden, dan volgt de hoogte van het punt op de band (ten opzichte van de as) een sinusgrafiek. De zijwaartse afwijking kan je beschrijven met een cosinus (een afwijking naar rechts kiezen we als positief).quote:
[..]
De as rolt inderdaad 1 meter vooruit. Masr de velg beschrijft dus een sinus functie. Dan zou je zeggen dat de snelheid tov de lucht (dus niet de weg) niet constant is.
De snelheid van het punt op je band is nu de vector die wordt opgespannen door de x en y component. Met de stelling van Pythagoras krijg je dan dat de lengte van deze somvector gelijk is aan cos²(t) + sin²(t) = 1. De grootte snelheid is dus constant (maar de richting verandert uiteraard).
Maar dit kan je natuurlijk ook op je klompen al aanvoelen. Als een stuk van je velg sneller zou gaan dan een ander stuk, schuift het dan in elkaar?
Ja het klopt dat rad/s constant is bij constante snelheid. Maar wat is dan de snelheid tov de x as? Die is niet constant.
Dat kan namelijk niet: de as beweegt met constante snelheid over de x as. 1 punt op de velg is het ene moment achter de as en later voor de as. Dan moet ie ergens sneller gaan dan de as snelheid.
Dat kan namelijk niet: de as beweegt met constante snelheid over de x as. 1 punt op de velg is het ene moment achter de as en later voor de as. Dan moet ie ergens sneller gaan dan de as snelheid.
Ter verduidelijking, het gaat niet om hoeksnelheid, maar snelheid tov de x as.
Wat we eigenlijk nodig hebben is een fiets en een stroboscoop
Wat we eigenlijk nodig hebben is een fiets en een stroboscoop
Oh zo.quote:
Ter verduidelijking, het gaat niet om hoeksnelheid, maar snelheid tov de x as.
Wat we eigenlijk nodig hebben is een fiets en een stroboscoop
Nou schrijf eerst eens de beweging op in referenceframe van middelpunt wiel en dan vanuit de weg.
Moet nit zo moeilik zijn toch?
