SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Kun je misschien uitleggen waarom je dat denkt en kun je het volledige plaatje geven? Want hier kan uiteraard niemand wat mee.quote:


Bij een kwadratische vergelijking is c volgens mij een constante en het staat ook in de post van thenxero.quote:Op zaterdag 13 juli 2013 18:33 schreef Thormodo het volgende:
[..]
Kun je misschien uitleggen waarom je dat denkt en kun je het volledige plaatje geven? Want hier kan uiteraard niemand wat mee.
Bijv.
x^2 + 10x - 39 = 0
c = -39
[ Bericht 2% gewijzigd door wiskundenoob op 13-07-2013 18:51:33 ]


Heb je het nu over de abc-formule of zo? c = -39 is nogal een rare statement, want er komt verder geen c voor in je post.quote:Op zaterdag 13 juli 2013 18:46 schreef wiskundenoob het volgende:
[..]
Bij een kwadratische vergelijking is c volgens mij een constante en het staat ook in de post van thenxero.
Bijv.
x^2 + 10x - 39 = 0
c = -39
Voor de abc-formule kun je x2 + 10x - 39 in ieder geval zien als ax2 + bx + c. Waarbij a=1, b=10 en c=-39.
Maar nogmaals, het is handig als je het volledige verhaal post...
[ Bericht 0% gewijzigd door Thormodo op 13-07-2013 19:00:32 ]


Ik heb wel een vermoeden waar die het over heeft. Maar zolang hij geen heldere vraag formuleert ga ik er niet meer op in.
Je mag blij zijn dat mensen je willen helpen. Maar als je er zelf geen moeite in steekt, krijg je ook geen moeite terug.
Je mag blij zijn dat mensen je willen helpen. Maar als je er zelf geen moeite in steekt, krijg je ook geen moeite terug.


Ok, dat valt dan wel weer meequote:Op zaterdag 13 juli 2013 17:10 schreef Thormodo het volgende:
[..]
Dingen afkraken is nogal een kansloze aangelegenheid als je niet eens in staat bent om even op te zoeken waar dat verslag nu daadwerkelijk van is.
Het is namelijk onderdeel van een 10 EC vak :http://www.studiegids.sci(...)ourses/course/29529/
Als je nagaat hoe weinig moeite je voor sommige vakken van 7,5 ects hoeft te doen
Klinkt interessantquote:Op zaterdag 13 juli 2013 17:22 schreef Thormodo het volgende:
[..]
Ik zeg ook niet dat het een briljant verslag is (alleen al het aantal spelfouten...). Misschien had ik beter Dale kunnen quoten. Overigens is het een onderwijsmodule, dus kunt je moeilijk iets op master niveau gaan maken.
Daarnaast was mijn PWS van hoger niveau; dat ging over Blackjack & Poker i.c.m. kansrekenen.


Kan je dit toelichten met wat concrete voorbeeldjes? Ik twijfel er niet aan dat je gelijk hebt maar het is handig om het wat concreter te maken.quote:Op zaterdag 13 juli 2013 17:24 schreef thenxero het volgende:
[..]
Dat bedoel ik dus. Het hoeft bij zo'n master natuurlijk ook geen technisch hoogstandje te zijn. Maar je mag wel verwachten dat het historisch correct is, met goede bronnen en zonder spelfouten. Bovendien laat de opbouw ook het een en ander te wensen over.
En dat ik niet zo'n hoge pet op heb van die master is (misschien niet geheel terecht) gebaseerd op de lesmethodes die ik tegenkom op middelbare scholen. Ik ga er dan even vanuit dat mensen die lesmethodes schrijven wel een master in education hebben. Toch kom ik aan de lopende band didactisch onverantwoorde sommen tegen. Als die master van hoog niveau is dan zou dat niet moeten kunnen.
Ook heb ik een keer gelezen in een blad (kan me de bron niet meer herinneren), dat het niveau van de education master zwaar onder druk stond.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL


Wat ik in veel boeken zie is het volgende. Eerst geven ze een "oriënterende som". Het idee is daar dat je gaat nadenken over iets voordat het wordt uitgelegd. In principe is daar nog niks mis mee (alhoewel het niet mijn smaak is, maar dat terzijde). Vervolgens staat er in een "theorie-vakje" (vaak een vrolijk kleurtje met een vrolijk mannetje ernaast) hetgeen wat je hebt uitgevonden in de oriënterende som, maar dan als algemene waarheid.quote:Op zaterdag 13 juli 2013 21:05 schreef Bram_van_Loon het volgende:
[..]
Kan je dit toelichten met wat concrete voorbeeldjes? Ik twijfel er niet aan dat je gelijk hebt maar het is handig om het wat concreter te maken.
Ze laten je bijvoorbeeld f(x)=2x primitiveren tot F(x)=x². Dan mag je F(1)-F(0) uitrekenen en krijg je dus 1 als uitkomst. Je moet ook even herkennen dat het gewoon een driehoekje is en de oppervlakte dus 2*1*1/2 = 1 is. Je ziet dus dat in dit geval de primitieves op 1 en 0 van elkaar afgetrokken gelijk is aan de oppervlakte onder de functie op [0,1]. Vervolgens staat eronder in het "theorie-vakje" simpelweg: De oppervlakte onder de grafiek f van a tot b bepaal je door F(b)-F(a) te berekenen.
Ja, dat is waar. Maar het staat er alsof je met één voorbeeld bewezen hebt dat dat zo is. Alsof je dom bent als je dan nog niet snapt waarom dat altijd waar is. Voor scholieren kan dat best leiden tot onzekerheid, want je weet niet meer wanneer je iets niet snapt of wanneer je het simpelweg niet kán snappen, omdat het niet is uitgelegd.
Een ander voorbeeld. Laatst kwam ik een 'bewijs' tegen waarom de afgeleide van ln(x) gelijk is aan 1/x. Dat ging ongeveer zo (uit mijn hoofd):
Stel y=ex, oftewel x=ln(y). Dan
(1)
Dus ook (?!)
Verder hebben we
Dus
Dus
(Hmm, het originele bewijs was nog erger, want daar werden x en y midden in het bewijs omgewisseld. Totaal overbodig en erg verwarrend. Ik moest het ook drie keer lezen. Ik kan echter niet reproduceren waar ze die wisseltruc deden, dus ik laat het maar zo.)
De (?!) stap vond ik nogal dubieus. Het vereist op zijn minst een rechtvaardiging als je claims maakt als
Bovendien, waarom nou niet gewoon op een heldere manier de kettingregel gebruiken? Ik zou het als volgt doen.
Merk op dat eln(x) = x. Beide kanten differentiëren naar x geeft met de kettingregel:
Dus
Klaar. Niet moeilijker maken dan dat het is!
En zo kan ik helaas nog wel even doorgaan. Nou, nog ééntje dan. Gegeven is een functie f(x) = e-x sin(x). Wat is de periode van deze functie? Beschouw nu g(x)=f(x)^2. Wat is de periode van g?
Nou dan is er alweer een probleem. Ten eerste werd periode in dat boek niet gedefinieerd, maar in mijn ogen is de periode het kleinste getal a zodanig dat f(x+a)=f(x), voor alle x in het domein. Dus wat is dan de periode


Hallo,
ik heb problemen met het begrijpen hoe ik een 'goodness of fit' doe met een Cox regression model. Ik heb via SPSS Cox-Snell residuals verkregen. Als ik papers raadpleeg (http://support.sas.com/re(...)dings13/431-2013.pdf , http://books.google.nl/bo(...)tribution%22&f=false )
dan zou ik een plot moeten krijgen waarbij op de x-axis de residuals staan, maar de y-axis is mij geheel onduidelijk.
Verder zou de residuals moeten lijken op een 'unit exponential distribution', maar ik kan nergens vinden wat de 'unit' toevoegt aan de exponential distribution.. mijn eigen interpretatie is dat het gewoon de exp. distr. is met lambda = 1.
Iemand die misschien toevallig iets af weet van proportional hazard models / cox regression?
Alvast bedankt!
ik heb problemen met het begrijpen hoe ik een 'goodness of fit' doe met een Cox regression model. Ik heb via SPSS Cox-Snell residuals verkregen. Als ik papers raadpleeg (http://support.sas.com/re(...)dings13/431-2013.pdf , http://books.google.nl/bo(...)tribution%22&f=false )
dan zou ik een plot moeten krijgen waarbij op de x-axis de residuals staan, maar de y-axis is mij geheel onduidelijk.
Verder zou de residuals moeten lijken op een 'unit exponential distribution', maar ik kan nergens vinden wat de 'unit' toevoegt aan de exponential distribution.. mijn eigen interpretatie is dat het gewoon de exp. distr. is met lambda = 1.
Iemand die misschien toevallig iets af weet van proportional hazard models / cox regression?
Alvast bedankt!


Sowieso vind ik heel het stelling-bewijs model een beetje, hoe zal ik het zeggen, ongepast (?) voor wiskunde-onderwijs. Een mooi of kort bewijs is vaak compleet wat anders dan een didactisch verantwoord verhaal, en ik zie liever een verhaal dat ik makkelijk onthoud dan een indrukwekkend bewijs, al is het alleen maar omdat ik na het eerste zelf eerder in staat ben zelf een bewijs te produceren.quote:


Het "definitie-stelling-bewijs verhaal" is essentieel voor wiskunde-onderwijs. Door al te veel in Jip- en Janneketaal te werken kan je uitleg op meerdere manieren interpreteren. Het beste werkt het volgens mij om alles zo exact mogelijk te houden en vervolgens met voorbeelden de theorie en de toepassingen te verduidelijken. Zijn kritiek ging echter veel verder dan dat.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL


Volgens mij mis je compleet het punt van mijn post. Bovendien zijn bewijzen niet gemaakt om indruk te wekken, maar om een zo eenvoudig en precies mogelijke redenering te geven. En het lijkt me sterk dat je makkelijker gegoochel onthoudt, dan een simpel bewijsje wat precies voortbouwt op wat je al weet.quote:Op maandag 15 juli 2013 22:46 schreef randomo het volgende:
[..]
Sowieso vind ik heel het stelling-bewijs model een beetje, hoe zal ik het zeggen, ongepast (?) voor wiskunde-onderwijs. Een mooi of kort bewijs is vaak compleet wat anders dan een didactisch verantwoord verhaal, en ik zie liever een verhaal dat ik makkelijk onthoud dan een indrukwekkend bewijs, al is het alleen maar omdat ik na het eerste zelf eerder in staat ben zelf een bewijs te produceren.


Bewijzen zijn niet bedoeld om indruk te wekken, maar vaak wordt er wel een zo kort mogelijk bewijs gegeven, waar je dan weer niet zoveel van leert. Een groot deel van mijn studieboeken en dictaten bestaat uit stellingen en bewijzen, en volgens mij kan de ruimte in veel gevallen beter gebruikt worden.quote:Op dinsdag 16 juli 2013 11:29 schreef thenxero het volgende:
[..]
Volgens mij mis je compleet het punt van mijn post. Bovendien zijn bewijzen niet gemaakt om indruk te wekken, maar om een zo eenvoudig en precies mogelijke redenering te geven. En het lijkt me sterk dat je makkelijker gegoochel onthoudt, dan een simpel bewijsje wat precies voortbouwt op wat je al weet.
Volgens mij is het meer een soort tik die veel wiskundigen hebben, om bij elke stelling een bewijs neer te zetten, ook al is het bewijs op zich niet zo leerzaam. Dan vind ik een 'bewijsschets' geven in veel gevallen nog mooier, omdat je studenten wel snel een idee geeft hoe het bewijs werkt, maar het nog steeds makkelijk leesbaar blijft.
Mijn post was inhoudelijk ook niet echt een reactie op jouw post, meer een licht gerelateerde ergernis die ik soms wel eens heb. Ik zal eens kijken of ik een voorbeeld kan vinden, dan kan ik het misschien wat duidelijker maken.


dan kan sneller; moet je alleen wel differentialen gehad hebbenquote:Op zaterdag 13 juli 2013 21:53 schreef thenxero het volgende:
[..]
Wat ik in veel boeken zie is het volgende. Eerst geven ze een "oriënterende som". Het idee is daar dat je gaat nadenken over iets voordat het wordt uitgelegd. In principe is daar nog niks mis mee (alhoewel het niet mijn smaak is, maar dat terzijde). Vervolgens staat er in een "theorie-vakje" (vaak een vrolijk kleurtje met een vrolijk mannetje ernaast) hetgeen wat je hebt uitgevonden in de oriënterende som, maar dan als algemene waarheid.
Ze laten je bijvoorbeeld f(x)=2x primitiveren tot F(x)=x². Dan mag je F(1)-F(0) uitrekenen en krijg je dus 1 als uitkomst. Je moet ook even herkennen dat het gewoon een driehoekje is en de oppervlakte dus 2*1*1/2 = 1 is. Je ziet dus dat in dit geval de primitieves op 1 en 0 van elkaar afgetrokken gelijk is aan de oppervlakte onder de functie op [0,1]. Vervolgens staat eronder in het "theorie-vakje" simpelweg: De oppervlakte onder de grafiek f van a tot b bepaal je door F(b)-F(a) te berekenen.
Ja, dat is waar. Maar het staat er alsof je met één voorbeeld bewezen hebt dat dat zo is. Alsof je dom bent als je dan nog niet snapt waarom dat altijd waar is. Voor scholieren kan dat best leiden tot onzekerheid, want je weet niet meer wanneer je iets niet snapt of wanneer je het simpelweg niet kán snappen, omdat het niet is uitgelegd.
Een ander voorbeeld. Laatst kwam ik een 'bewijs' tegen waarom de afgeleide van ln(x) gelijk is aan 1/x. Dat ging ongeveer zo (uit mijn hoofd):
Stel y=ex, oftewel x=ln(y). Dan
(1)
Dus ook (?!)
Verder hebben we
Dus
Dus
(Hmm, het originele bewijs was nog erger, want daar werden x en y midden in het bewijs omgewisseld. Totaal overbodig en erg verwarrend. Ik moest het ook drie keer lezen. Ik kan echter niet reproduceren waar ze die wisseltruc deden, dus ik laat het maar zo.)
De (?!) stap vond ik nogal dubieus. Het vereist op zijn minst een rechtvaardiging als je claims maakt als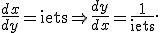
Bovendien, waarom nou niet gewoon op een heldere manier de kettingregel gebruiken? Ik zou het als volgt doen.
Merk op dat eln(x) = x. Beide kanten differentiëren naar x geeft met de kettingregel:
Dus
Klaar. Niet moeilijker maken dan dat het is!
En zo kan ik helaas nog wel even doorgaan. Nou, nog ééntje dan. Gegeven is een functie f(x) = e-x sin(x). Wat is de periode van deze functie? Beschouw nu g(x)=f(x)^2. Wat is de periode van g?
Nou dan is er alweer een probleem. Ten eerste werd periode in dat boek niet gedefinieerd, maar in mijn ogen is de periode het kleinste getal a zodanig dat f(x+a)=f(x), voor alle x in het domein. Dus wat is dan de periode?
f(x)=ln(x)
Stel ln(x)=t => x=e^t
Bereken dy/dx: d(ln(x))/dx = dt/d(et) = 1dt/etdt = 1dt/etdt = 1/et = 1/x


Vaak wordt ln(x) = ∫1x t-1dt geïntroduceerd als deze integraal en dan volgt direct uit de hoofdstelling van de integraalrekening dat d(ln(x))/dx = 1/x. Daarna kan dan exp(x) gedefinieerd worden als de inverse functie van ln(x) en volgt met de kettingregel ook gemakkelijk dat d(exp(x))/dx = exp(x).quote:Op zaterdag 13 juli 2013 21:53 schreef thenxero het volgende:
[..]
Een ander voorbeeld. Laatst kwam ik een 'bewijs' tegen waarom de afgeleide van ln(x) gelijk is aan 1/x. Dat ging ongeveer zo (uit mijn hoofd):
Dit ligt meer voor de hand dan de omgekeerde weg volgen en eerst de afgeleide van ax behandelen (met a > 0), want om aan te tonen dat d(ax)/dx = ln(a)·ax heb je sowieso natuurlijke logarithmen nodig en zou je ook eerst aan moeten tonen dat limh→0 (ah − 1)/h = ln(a).


Helemaal mee eens. limh→0 (ah − 1)/h = ln(a) werd ook nergens aangetoond.quote:Op woensdag 17 juli 2013 16:47 schreef Riparius het volgende:
[..]
Vaak wordt ln(x) = ∫1x t-1dt geïntroduceerd als deze integraal en dan volgt direct uit de hoofdstelling van de integraalrekening dat d(ln(x))/dx = 1/x. Daarna kan dan exp(x) gedefinieerd worden als de inverse functie van ln(x) en volgt met de kettingregel ook gemakkelijk dat d(exp(x))/dx = exp(x).
Dit ligt meer voor de hand dan de omgekeerde weg volgen en eerst de afgeleide van ax behandelen (met a > 0), want om aan te tonen dat d(ax)/dx = ln(a)·ax heb je sowieso natuurlijke logarithmen nodig en zou je ook eerst aan moeten tonen dat limh→0 (ah − 1)/h = ln(a).


Overigens kan ik het wel met de hand uitrekenen, de primitieve is immers bekend. Maar even in mijn GR gegooid, het antwoord voldoet weinig aan de verwachtingen.


WolframAlpha snapt dit prima, maar jij voert het kennelijk verkeerd in, kijk maar hoe het wel werkt.quote:


Wat is er dan precies mis met mijn stukje LaTeX (of TeX, hoe die code ook mag heten)?quote:Op woensdag 17 juli 2013 17:08 schreef Riparius het volgende:
[..]
WolframAlpha snapt dit prima, maar jij voert het kennelijk verkeerd in, kijk maar hoe het wel werkt.
| 1 | 1-4(\int_0^1(\sqrt{1-x^2})dx - 2\int_0^{1/2}(\sqrt{1-x^2})dx) |
[ Bericht 5% gewijzigd door #ANONIEM op 17-07-2013 17:22:42 ]


Niets, en als ik dat invoer in WolframAlpha werkt het ook, dus kennelijk had je dan eerst iets anders.quote:Op woensdag 17 juli 2013 17:18 schreef Amoeba het volgende:
[..]
Wat is er dan precies mis met mijn stukje LaTeX (of TeX, hoe die code ook mag heten)?
[ code verwijderd ]


Amoeba, wat voor cijfer heb jij gekregen voor jouw PWS?
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL


Een 7 man. Ik voel me hard genaaid.quote:Op woensdag 17 juli 2013 18:51 schreef Bram_van_Loon het volgende:
Amoeba, wat voor cijfer heb jij gekregen voor jouw PWS?
Nu snap ik er ook niks meer van. Net kon hij er niet veel van maken.quote:Op woensdag 17 juli 2013 18:47 schreef Riparius het volgende:
[..]
Niets, en als ik dat invoer in WolframAlpha werkt het ook, dus kennelijk had je dan eerst iets anders.


 Op
Op