SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
quote:Op vrijdag 27 juli 2012 15:09 schreef Bram_van_Loon het volgende:
Ik heb een vraagje over een triple-integraal (nu ja, eigenlijk een dubbelintegraal na het wegwerken van een variabele) die is uitgedrukt in polaire coördinaten.
Ik begrijp niet waarom die 2y en 1 zijn verdwenen. Ik had op de onderste regel (4-r²-2y-1) verwacht in plaats van (4-r²).
Wat zie ik over het hoofd?
Die dxdy wordt rdrdθ en x²+y²=r²
Hetgeen wat voor die dxdy staat moet dan toch blijven staan met dat laatste formuletje toegepast?
quote:
Het zijn geen standaardpoolcoördinaten; het centrum is niet (0,0).
quote:
Dat had ik overwogen maar ik zou graag wat meer uitleg krijgen zodat ik zeker weet dat ik het goed begrijp.
quote:
r is de afstand van (x,y) tot (0,-1); als je de afleiding achter de r die erbij komt begrijpt, kun je makkelijk aantonen dat die er nu ook bijkomt; snap niet hoe dat vraagtekens op kan roepen
quote:
Begrijp ik het goed dat bij de omzetting van de cartesische coördinaten naar de polaire coördinaten de oorsprong van het polaire assenstelsel op punt (0,-1,0) komt te liggen?
quote:
quote:
Ik verwees met de coördinaat naar het cartesische stelsel wat daar staat, dus nam ik de z mee.
Belangrijker, begrijp ik goed dat de oorsprong van het polaire stelsel daar dan komt te liggen ((0,-1) of (0,-1,0))?
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Normaal heb je de transformatie
x=r*cos θ
y=r*sin θ
Nu heb je de transformatie
x=r*cos θ
y=r*sin θ-1
Dat maakt voor de jacobiaan niet uit.
x=r*cos θ
y=r*sin θ
Nu heb je de transformatie
x=r*cos θ
y=r*sin θ-1
Dat maakt voor de jacobiaan niet uit.
Dan had ik het wel goed begrepen en zocht ik slechts bevestiging.quote:
Op 
Dank je.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Ik moet de volgende som als een enkele logaritme schrijven.
Maar ik kom er echt helemaal niet uit.
De som is als volgt:
1/4log6z + 7log6y - log6x
de zessen achter de log horen bij de log zelf. Ik kon helaas de 6 niet kleiner schrijven.
Het antwoord moet in zo een vorm komen: log...(...)
Maar ik kom er echt helemaal niet uit.
De som is als volgt:
1/4log6z + 7log6y - log6x
de zessen achter de log horen bij de log zelf. Ik kon helaas de 6 niet kleiner schrijven.
Het antwoord moet in zo een vorm komen: log...(...)
Je kunt toch gewoon bovenstaande rekenregels toepassen?
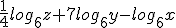
Pas de 3e regel toe: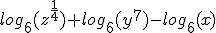
(je kunt eventueel 
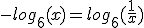doen)
Dan de eerste regel: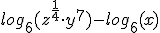
De laatste stap mag je zelf proberen, daar leer je het meeste van
Pas de 3e regel toe:
Dan de eerste regel:
De laatste stap mag je zelf proberen, daar leer je het meeste van
. Er is verder niets meer te vereenvoudigen?
Nee, ik doe TWINFO, dan heb je niks aan vakken van niveau 2 (die tellen niet mee ofzo). Ik zou het misschien uit eigen interesse wel willen volgen, maar dit jaar wordt vrij druk, ik wil zoveel mogelijk studiepunten halen zodat ik volgend jaar misschien een halfjaartje in het buitenland kan gaan studeren.quote:
[..]
Ga je volgend jaar analyse in meerdere variabelen doen? (die boeken die daarbij horen vind ik afschuwelijk, die zal ik je niet aanraden).
(Beetje late reactie, ik was op vakantie
)
Okequote:Op dinsdag 31 juli 2012 20:50 schreef kutkloon7 het volgende:
[..]
Nee, ik doe TWINFO, dan heb je niks aan vakken van niveau 2 (die tellen niet mee ofzo). Ik zou het misschien uit eigen interesse wel willen volgen, maar dit jaar wordt vrij druk, ik wil zoveel mogelijk studiepunten halen zodat ik volgend jaar misschien een halfjaartje in het buitenland kan gaan studeren.
(Beetje late reactie, ik was op vakantie
. Het vak is ook niet erg aan te raden hoor (in ieder geval niet als het hetzelfde gebleven is). 't Is wel nuttig als je natuurkunde erbij doet.
Bij het vinden van een limiet moet ik in een som voor x het volgende invullen:
x--> -3^- De laatste min staat dus rechts erboven. Wat bedoelen ze ermee?
x--> -3^- De laatste min staat dus rechts erboven. Wat bedoelen ze ermee?
stel je hebt 1/(x+3) dan gaat dat naar -oneindig of +oneindig, afhankelijk van of x van links of van rechts naar -3 gaat. Als er x -> -3- gaat, dan betekent het dat x van links komt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
g(x)= x+6 if x < -3
g(x)= (x+1)/(x+2) if x is groter of gelijk aan -3
lim x --> -3^- g(x)=...
lim x --> -3^+ g(x)=...
lim x --> -3 g(x)=...
Ik weet echt niet wat ik hier moet doen. Kan ik ergens iets vinden hoe ik een limiet moet berekenen? Ik heb mijn wiskunde a samengevat boekje bij me maar ik kan er niks over vinden.
g(x)= (x+1)/(x+2) if x is groter of gelijk aan -3
lim x --> -3^- g(x)=...
lim x --> -3^+ g(x)=...
lim x --> -3 g(x)=...
Ik weet echt niet wat ik hier moet doen. Kan ik ergens iets vinden hoe ik een limiet moet berekenen? Ik heb mijn wiskunde a samengevat boekje bij me maar ik kan er niks over vinden.
Er is een formele definitie voor, maar meestal is het niet de bedoeling dat je die gebruikt.quote:
g(x)= x+6 if x < -3
g(x)= (x+1)/(x+2) if x is groter of gelijk aan -3
lim x --> -3^- g(x)=...
lim x --> -3^+ g(x)=...
lim x --> -3 g(x)=...
Ik weet echt niet wat ik hier moet doen. Kan ik ergens iets vinden hoe ik een limiet moet berekenen? Ik heb mijn wiskunde a samengevat boekje bij me maar ik kan er niks over vinden.
limx -> y g(x) = c kan je intuïtief zien als: "als x erg dicht bij y komt, komt g(x) erg dicht bij c". Voor zogenaamde continue functies (dit zijn ongeveer alle functies die je normaal gebruikt, polynomen, sinus, cosinus, en zelfs quotiënten, op alle punten waar datgene waardoor gedeeld wordt niet nul is) geldt limx -> y g(x) = g(y). Oftewel, je kan de waarde waar x naar nadert gewoon invullen in g, als g op dat punt gedefinieerd is.
Het is meestal iets lastiger, omdat de noemer bijvoorbeeld nul nadert op het punt waar je de limiet moet nemen. Bijvoorbeeld: limx -> -2 (x2 - 4) / (x + 2)
Dan kan je ofwel de regel van l'Hopital toepassen, ofwel het quotiënt vereenvoudigen:
Vereenvoudigen:
limx -> -2 (x2 - 4) / (x + 2) = limx -> -2 (x + 2)(x - 2) / (x + 2) = limx -> -2 x - 2
Deze functie is continu, dus kan je stellen limx -> -2 x - 2 = -4
De regel van l'Hopital houdt in dat als in een quotiënt de noemer naar nul gaat, je zowel de teller en de noemer mag differentiëren, van het resultaat de limiet mag nemen, en dat deze limiet hetzelfde is als de eerste limiet (die je dus niet zo kon berekenen).
Dus limx -> -2 (x2 - 4) / (x + 2) = limx -> -2 2x = -4
(De laatste stap heb ik weer de continuïteit gebruikt).
In de gevallen die jij geeft, bekijk je een limiet waarbij x een waarde nadert 'van een bepaalde kant'. Als x -> -3-, betekent het, zoals GlowMouse zei, dat x van links komt. Je mag dus stellen x < -3 (wat het geval is als x -3 nadert, maar van links komt) en je kan de eerste definitie voor g(x) gebruiken (g(x) = x + 6).
[ Bericht 7% gewijzigd door kutkloon7 op 01-08-2012 13:00:29 ]
Zoals ik het zie hoef ik bij geen enkele van mijn opgaves de l'Hopital regel te gebruiken.
bij lim--> -3 gebruik ik dan de g(x)= (x+1)/(x+2)
Maar verder snap ik het echt niet wat ik nu moet doen. Sorry dat ik zo achterlijk overkom
Moet ik dan bij x gewoon -3 invullen?
bij lim--> -3 gebruik ik dan de g(x)= (x+1)/(x+2)
Maar verder snap ik het echt niet wat ik nu moet doen. Sorry dat ik zo achterlijk overkom
Moet ik dan bij x gewoon -3 invullen?
Klopt, maar misschien handig om te weten, op examens komen die meestal wel.quote:
Zoals ik het zie hoef ik bij geen enkele van mijn opgaves de l'Hopital regel te gebruiken.
Dat kan niet. Ik zei dat de meeste functies continu zijn, wat op zich klopt, maar bij zo'n functiedefinitie als:quote:Moet ik dan bij x gewoon -3 invullen?
als x < -3 dan ...
anders ...
Kan het zijn dat de functie op -3 niet continu is:
Bijvoorbeeld limx -> -3 g(x) bestaat niet, omdat de bovenlimiet (x -> -3+) verschillend is van de onderlimiet (x -> -3-). Dan heb je dus dit idee:
En je kan niet zeggen dat als x naar -3 gaat, g(x) naar een bepaalde waarde nadert. De bovenlimiet lim x -> 3+ g(x) is immers 3, en de onderlimiet lim x -> 3+ g(x) is 2 (die kon je overigens beide vinden door gewoon invullen zie ik nu, mijn uitleg was niet echt relevant voor de limieten die jij gaf, het geeft de indruk dat die functie g(x) continu zou zijn, maar dat is niet zo op het punt -3!). Maar misschien alsnog handig voor andere limieten.
Heb je trouwens geen vakantie, of moet je iets inhalen?
Ik ben bezig met ee wiskunde cursus voor mijn opleiding.quote:
[..]
Klopt, maar misschien handig om te weten, op examens komen die meestal wel.
[..]
Dat kan niet. Ik zei dat de meeste functies continu zijn, wat op zich klopt, maar bij zo'n functiedefinitie als:
als x < -3 dan ...
anders ...
Kan het zijn dat de functie op -3 niet continu is:
Bijvoorbeeld limx -> -3 g(x) bestaat niet, omdat de bovenlimiet (x -> -3+) verschillend is van de onderlimiet (x -> -3-). Dan heb je dus dit idee:
[ afbeelding ]
En je kan niet zeggen dat als x naar -3 gaat, g(x) naar een bepaalde waarde nadert. De bovenlimiet lim x -> 3+ g(x) is immers 3, en de onderlimiet lim x -> 3+ g(x) is 2 (die kon je overigens beide vinden door gewoon invullen zie ik nu, mijn uitleg was niet echt relevant voor de limieten die jij gaf, het geeft de indruk dat die functie g(x) continu zou zijn, maar dat is niet zo op het punt -3!). Maar misschien alsnog handig voor andere limieten.
Heb je trouwens geen vakantie, of moet je iets inhalen?
Klopt het dat je bij de limieten krijgt
g(x)= x+6 if x < -3
g(x)= (x+1)/(x+2) if x is groter of gelijk aan -3
lim x --> -3^- g(x)=...hier gebruik je x+6 de uitkomst is nu 3
lim x --> -3^+ g(x)=... hier gebruik je (x+1)/(x+2), de uitkomst is nu 2
lim x --> -3 g(x)=... Hier gebruik je (x+1)/(x+2), de uitkomst is ook 2
Klopt dit?
Of de [ tex] tag, die is best makkelijk te gebruiken. Die herkent de ^ als superscript en de _ als subscript. Meerdere (super of sub) karakters die bij elkaar horen groepeer je met {accolades}. Een pijl naar rechts is \rightarrow.
vb:
y^2 geeft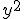
en y_2 geeft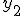 
y^{2x+1} geeft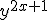
vb:
y^2 geeft
y^{2x+1} geeft
Ik had begrepen dat hier nog geen volledige LaTeX-functionaliteit is, dat je daarvoor een andere website moet gebruiken, die plaatjes moet hosten en vervolgens van daar die plaatjes laadt? Ik vind het er in ieder geval niet zo fraai uitzien zoals het wordt afgedrukt met behulp van die tex-tag.
Deze plugin zou gemakkelijk voor dit forum te gebruiken moeten zijn: http://www.mathjax.org/
Deze plugin zou gemakkelijk voor dit forum te gebruiken moeten zijn: http://www.mathjax.org/
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Gewoon simpelweg de tex-tag gebruiken, willekeurige LaTeX-code gebruiken (willekeurig in de zin van eender welke code die met normale software een output geeft) en dan een fraai plaatje op het scherm krijgen lukt toch nog niet? Of heb ik iets gemist? Ik herinner me een uitgebreide uitleg van Glowmouse hoe je, met behulp van een website van hem, die LaTeX gebruikt en dat je dan de code met een img-tag moet plaatsen.
Hoe dan ook, ik wijs er maar even op dat dit een gebruiksvriendelijke en efficiënte plugin is die het overwegen waard is. De verantwoordelijken moeten maar zien of dat ze het willen implementeren.
Hoe dan ook, ik wijs er maar even op dat dit een gebruiksvriendelijke en efficiënte plugin is die het overwegen waard is. De verantwoordelijken moeten maar zien of dat ze het willen implementeren.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Er is hier wel TeX-support via de [tex ] tag; je moet alleen de 'codes' weten indien je speciale constructies wilt maken (wortel, sommatie, breuk, etc).
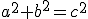
Als je mijn post quote dan zie je de code staan.
Als je mijn post quote dan zie je de code staan.
Die oplossing van Glowmouse was er voordat de tex-tags geïntroduceerd waren. Nu is dat compleet overbodig. En volgens mij had die site niet meer functionaliteit dan de huidige tex-tags.quote:
Gewoon simpelweg de tex-tag gebruiken, willekeurige LaTeX-code gebruiken (willekeurig in de zin van eender welke code die met normale software een output geeft) en dan een fraai plaatje op het scherm krijgen lukt toch nog niet? Of heb ik iets gemist? Ik herinner me een uitgebreide uitleg van Glowmouse hoe je, met behulp van een website van hem, die LaTeX gebruikt en dat je dan de code met een img-tag moet plaatsen.
Hoe dan ook, ik wijs er maar even op dat dit een gebruiksvriendelijke en efficiënte plugin is die het overwegen waard is. De verantwoordelijken moeten maar zien of dat ze het willen implementeren.
Je kan prima een plaatje uploaden buiten de tex tags met img-tags. Dus ik zie niet in waarom je dat binnen je tex-tags zou willen. Tenzij je hele posts wil maken in LaTeX-stijl... maar dat lijkt me onnodig ingewikkeld. Het doel van die tex-tags is dat je wiskundige formules makkelijk kunt typen.
Handig om te weten. Dank je.quote:
Er is hier wel TeX-support via de [tex ] tag; je moet alleen de 'codes' weten indien je speciale constructies wilt maken (wortel, sommatie, breuk, etc).
Als je mijn post quote dan zie je de code staan.
Ik heb de indruk dat de plaatjes er wel wat lelijk uitzien: lage resolutie en ook niet zo'n ideale verhoudingen als wat mogelijk is (die superscript en subscript zijn veel te groot, ik vind bijv. de integralen er ook niet fraai uitzien op de website waar jij naar linkt). Ik vind de plaatjes zoals je ze met die andere plugin krijgt fraaier. Nogmaals, ze moeten zelf maar zien wat ze willen doen, ik wijs slechts op de mogelijkheid zodat ze weten dat dat een alternatief is. Uiteraard is die plugin gratis, anders zou ik die niet aanraden.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Hij doet wel een groot beroep op de bandbreedte van bezoekers. Vergeet ook niet dat we meerdere lay-outs en mobiele bezoekers hebben.quote:
[..]
Uiteraard is die plugin gratis, anders zou ik die niet aanraden.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik moet de inverse van de volgende functie krijgen, maar ik kom er niet uit.
De functie is als volgt en de volgende stappen heb ik al gedaan:
f(x)= (3x-5)/(4x+1)
y= (3x-5)/(4x+1)
x= (3y-5)/(4y+1)
x (4y+1)= (3y-5)
4yx +x = 3y-5
x= 3y-5 -4yx
Verder dan dit kom ik niet.
De functie is als volgt en de volgende stappen heb ik al gedaan:
f(x)= (3x-5)/(4x+1)
y= (3x-5)/(4x+1)
x= (3y-5)/(4y+1)
x (4y+1)= (3y-5)
4yx +x = 3y-5
x= 3y-5 -4yx
Verder dan dit kom ik niet.
Tot hier ging het goed. De bedoeling is dat je y hieruit 'oplost', i.e. dat je y uitdrukt in x. Daarvoor breng je eerst alle termen met y naar het linkerlid en alle termen zonder y naar het rechterlid. Nu maar weer even zelf proberen.quote:
Ik moet de inverse van de volgende functie krijgen, maar ik kom er niet uit.
De functie is als volgt en de volgende stappen heb ik al gedaan:
f(x)= (3x-5)/(4x+1)
y= (3x-5)/(4x+1)
x= (3y-5)/(4y+1)
x (4y+1)= (3y-5)
4yx +x = 3y-5
4yx-3y= -x-5 :Squote:
[..]
Tot hier ging het goed. De bedoeling is dat je y hieruit 'oplost', i.e. dat je y uitdrukt in x. Daarvoor breng je eerst alle termen met y naar het linkerlid en alle termen zonder y naar het rechterlid. Nu maar weer even zelf proberen.
y(4x-3)= -x-5quote:
[..]
Juist. En haal nu in het linkerlid y buiten haakjes. Zie je daarna hoe je verder moet?
y= (-x-5)/(4x-3)
Is dit het?
4yx - 3-y = -x - 5quote:
y(4x-3) = -x - 5
Ja dus. Maar doe me/ons een lol, en leer wat TeX. Breuken zonder TeX zijn niet te lezen.quote:
[..]
y(4x-3)= -x-5
y= (-x-5)/(4x-3)
Is dit het?
[ Bericht 16% gewijzigd door #ANONIEM op 01-08-2012 20:49:03 ]
Ja. Je zou nog kunnen schrijven f-1(x) = (-x-5)/(4x-3) om aan te geven dat dit de inverse is van je f(x).quote:
[..]
y(4x-3)= -x-5
y= (-x-5)/(4x-3)
Is dit het?
Oh, die had ik niet zien staan.quote:
[..]
voor de x-5 moet nog een - toch?
Hierbij moet ik het domein en het bereik bepalen.
Het domein is alles behalve 3/4 want de noemer mag niet 0 worden.
Hoe bepaal ik het bereik van bovenstaande functie?
Wat voor figuur is de grafiek van je functie als je x alle toegestane waarden (op R) aan laat nemen?quote:
Hierbij moet ik het domein en het bereik bepalen.
Het domein is alles behalve 3/4 want de noemer mag niet 0 worden.
Hoe bepaal ik het bereik van bovenstaande functie?
En daarmee ook de vraag, welke waarde(n) zijn toegestaan, en waarom?quote:
[..]
Wat voor figuur is de grafiek van je functie als je x alle toegestane waarden (op R) aan laat nemen?
Ja. En wat zijn de vergelijkingen van de asymptoten van die hyperbool? En wat kun je zeggen over het domein van je oorspronkelijke functie? En wat is het verband tussen domein en bereik van je oorspronkelijke functie en van je inverse functie? Kijk anders even hier.quote:
Het domein van de oorspronkelijke functiequote:
[..]
Ja. En wat zijn de vergelijkingen van de asymptoten van die hyperbool? En wat kun je zeggen over het domein van je oorspronkelijke functie? En wat is het verband tussen domein en bereik van je oorspronkelijke functie en van je inverse functie? Kijk anders even hier.
f(x)= (3x-5)/(4x+1)
is 1/4.
Nee, het is R\{-¼}. Dit is dan tevens het bereik van je inverse functie, en dat had je ook gemakkelijk in het plaatje van WolframAlpha kunnen zien.quote:
[..]
Het domein van de oorspronkelijke functie
f(x)= (3x-5)/(4x+1)
is 1/4.
