SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Dit is een bekende kwestie, waarvoor je niet naar een TV-documentaire als bron hoeft te verwijzen. Het bewijst niet dat Einstein niet goed (genoeg) was in wiskunde, dat is gewoon een (weliswaar hardnekkige) urban myth. En zoals uit mijn citaat blijkt was Lorentz, en niemand anders, voor Einstein de unsung hero van de moderne fysica.quote:Op woensdag 11 juli 2012 19:25 schreef Mathemaat het volgende:
[..]
Nee, wat ik in een documentaire heb gezien, is dat Einstein een college heeft gegeven aan een Duitse universiteit en Hilbert zat toen in het publiek. Het was Einstein toentertijd nog niet gelukt om de juiste vergelijkingen (of vergelijking) te vinden voor de algemene relativiteitstheorie, dus heeft Hilbert het ook maar gedaan. Maar omdat het Einsteins idee was, heeft Hilbert de eer maar aan Einstein gegeven.
Dat is wel een goede introductie in de "universiteitswiskunde" inderdaad.quote:
[..]
Euclidische meetkunde stelt in de theoretische wiskunde niet meer zoveel voor. Dus je kan je tijd beter besteden door bijvoorbeeld te beginnen met dit boek: http://www.bol.com/nl/p/mathematical-proofs/1001004005475727
Het is een goed boek waarin aan alle gebieden binnen de wiskunde een begin wordt gemaakt. Je leert ook erin bewijzen schrijven en lezen.
Als je echt wat aan Euclidische meetkunde wil gaan doen kun je m.i. beter beginnen met de boeken van Coxeter (Geometry Revisited en Introduction to Geometry). Of Hoofdstukken uit de elementaire meetkunde van Bottema natuurlijk. Verder nog Johnson, Advanced Euclidean Geometry en Altshiller-Court, College Geometry (beide Dover reprints).quote:
[..]
Ik ben reeds geslaagd voor mijn wiskunde B examen (met een 8). Voor het examen heb ik me k a p o t geoefend op die examens, en dan vooral de meetkundige opgaven.
[ Bericht 7% gewijzigd door Riparius op 12-07-2012 06:00:39 ]
Dat boek heb ik dit jaar ook gebruikt. Het is wel vrij basis, maar wel een mooie introductie. Vooral inderdaad in de stijl, die is erg kenmerkend voor universitaire wiskunde, zonder dat het echt moeilijk wordt.quote:
[..]
Euclidische meetkunde stelt in de theoretische wiskunde niet meer zoveel voor. Dus je kan je tijd beter besteden door bijvoorbeeld te beginnen met dit boek: http://www.bol.com/nl/p/mathematical-proofs/1001004005475727
Het is een goed boek waarin aan alle gebieden binnen de wiskunde een begin wordt gemaakt. Je leert ook erin bewijzen schrijven en lezen.
Wat thenxzero dus ook al zei
Analyse B niet gehaald?quote:Op woensdag 11 juli 2012 22:36 schreef kutkloon7 het volgende:
Boh, het gaat niet zo best met mijn studie
Eerste jaar is het altijd effe wennen. De tweede jaar is nog moeilijker. Je moet harder werken en gewoon door blijven gaan of een andere studie kiezenquote:
Boh, het gaat niet zo best met mijn studie
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Voor iedereen die er belang in stelt: ik heb mijn post over goniometrische identiteiten van enige tijd geleden bewerkt tot een PDF die wat beter leesbaar is en uiteraard ook goed is af te drukken. Je kunt het hier bekijken en desgewenst downloaden.
Een 5quote:
Op 
. Hoe weet jij dat die cijfers net bekend zijn dan?Ik heb dat altijd de laatste repetitie/tentamenweek, dat ik alles verpestquote:
[..]
Eerste jaar is het altijd effe wennen. De tweede jaar is nog moeilijker. Je moet harder werken en gewoon door blijven gaan of een andere studie kiezen
quote:
Voor iedereen die er belang in stelt: ik heb mijn post over goniometrische identiteiten van enige tijd geleden bewerkt tot een PDF die wat beter leesbaar is en uiteraard ook goed is af te drukken. Je kunt het hier bekijken en desgewenst downloaden.
Ga ik zeker even uitprinten zo!
Balen. Was maar een gokje, ik weet alleen dat je analyse B en modsim gedaan hadquote:
[..]
Een 5
. Het 2e jaar vond ik overigens makkelijker, en het derde jaar nog wat makkelijker. Als je eenmaal de smaak te pakken hebt blijf je wel rollen. Het niveau wordt niet lager, maar het neemt ook niet zoveel toe als je van de middelbare school naar de uni gaat ofzo.
De laatste tentamenweek verkloot ik ook altijd een beetje. Gewoon 8en halen op je eerste deeltentamen, heb je een vangnetje
. Ik deed nog wat extra vakken, dus ik zat nog 3 tentamens te maken toen ik mijn bsc al had... dan mis je wel een beetje motivatie .
Hehe, kan me voorstellen. Ik moet zeggen dat ik ook even heb gekeken naar elementaire getaltheorie een tijd geleden. Ik had toen net een stuk gelezen in 'Getaltheorie voor beginners' van Frits Beukers (die trouwens dat vak ook geeft, maar bij dat vak gebruik je volgens mij niet dat boek), en het tentamen was best goed te doen, ik hoop dat dat bij de andere vakken ook zo is.quote:
[..]
Balen. Was maar een gokje, ik weet alleen dat je analyse B en modsim gedaan had
Het 2e jaar vond ik overigens makkelijker, en het derde jaar nog wat makkelijker. Als je eenmaal de smaak te pakken hebt blijf je wel rollen. Het niveau wordt niet lager, maar het neemt ook niet zoveel toe als je van de middelbare school naar de uni gaat ofzo.
De laatste tentamenweek verkloot ik ook altijd een beetje. Gewoon 8en halen op je eerste deeltentamen, heb je een vangnetje
Overigens vond ik lineaire algebra b en analyse b ook vrij goed te doen. Het was een beetje jammer dat ik ook een informaticavak doe en mijn practicumpartner, die per se het eerste deel wou doen (dus waarop ik moest wachten), er twee dagen voor de deadline achter kwam dat hij niet in staat was met iets bruikbaars aan te komen
Uiteraard viel die deadline precies in de tentamenweek wiskunde, waardoor ik zo goed als niet geleerd heb. Heb ik een 5 gehaald, waardoor ik het vak net niet haal (want er is geen deeltentamen bij dat vak). En bij de her ben ik op vakantie.Dus ja, het is niet dat het nou zo'n vreselijk moeilijk vak is waardoor ik het niet gehaald heb, meer door 'omstandigheden'. Maar het blijft vervelend, vooral omdat ik volgend jaar al eigenlijk geen tijd heb om het vak in te halen.
Maar goed, genoeg gehuild
Getaltheorie heb ik zelf niet gedaan, maar het scheen erg makkelijk te zijn... hoorde van allemaal mensen dat ze >9 hadden .
Wat je ook kan doen is Analyse B volgend jaar in de hertentamenweek maken. Met een beetje zelfstudie moet dat wel lukken.
. Wat je ook kan doen is Analyse B volgend jaar in de hertentamenweek maken. Met een beetje zelfstudie moet dat wel lukken.
poeh, die entrance examination mathematics level 3 for econometrics sample questions van de EUR is wel een niveautje hoger dan vwo wiskunde B, voor mij tenminste.
ik kom er weer niet uit bij vraag 3b, geen idee waar te beginnen eigenlijk:
f(x) = e^(4x-x^2+px^3)
Determine all values of p for which f(x) has exactly two extremes. Het antwoord is trouwens p < 1/12.
Ik dacht dat ik wel goed was in wiskunde, VWO wiskunde B is een makkie voor mij, maar misschien toch niet dan ;-)
ik kom er weer niet uit bij vraag 3b, geen idee waar te beginnen eigenlijk:
f(x) = e^(4x-x^2+px^3)
Determine all values of p for which f(x) has exactly two extremes. Het antwoord is trouwens p < 1/12.
Ik dacht dat ik wel goed was in wiskunde, VWO wiskunde B is een makkie voor mij, maar misschien toch niet dan ;-)
Stap 1. Hoe vind je de extreme waarden van f?quote:
poeh, die entrance examination mathematics level 3 for econometrics sample questions van de EUR is wel een niveautje hoger dan vwo wiskunde B, voor mij tenminste.
ik kom er weer niet uit bij vraag 3b, geen idee waar te beginnen eigenlijk:
f(x) = e^(4x-x^2+px^3)
Determine all values of p for which f(x) has exactly two extremes. Het antwoord is trouwens p < 1/12.
Ik dacht dat ik wel goed was in wiskunde, VWO wiskunde B is een makkie voor mij, maar misschien toch niet dan ;-)
Dit is toch echt standaardwerk hoor, zou je als VWO'er geen moeite mee mogen hebben. Uiteraard bepaal je eerst de afgeleide van de functie (denk aan de kettingregel):quote:
poeh, die entrance examination mathematics level 3 for econometrics sample questions van de EUR is wel een niveautje hoger dan vwo wiskunde B, voor mij tenminste.
ik kom er weer niet uit bij vraag 3b, geen idee waar te beginnen eigenlijk:
f(x) = e^(4x - x^2 + px^3)
Determine all values of p for which f(x) has exactly two extremes. Het antwoord is trouwens p < 1/12.
Ik dacht dat ik wel goed was in wiskunde, VWO wiskunde B is een makkie voor mij, maar misschien toch niet dan ;-)
f'(x) = (4 - 2x + 3px2)∙e^(4x - x2 + px3)
Nu moet de afgeleide nul zijn voor precies twee waarden van x, want er moeten twee extremen zijn. Je weet ook dat een e-macht nooit nul is, dus moet gelden:
4 - 2x + 3px2 = 0
oftewel:
3px2 - 2x + 4 = 0
Dit is een vierkantsvergelijking in x (voor p ≠ 0). Nu moet je je afvragen onder welke voorwaarde(n) een vierkantsvergelijking met reële coëfficiënten twee verschillende (reële) oplossingen heeft. Dat is het geval als de discriminant positief is. Dus wordt de voorwaarde:
(-2)2 - 4∙(3p)∙4 > 0
4 - 48p > 0
4 > 48p
48p < 4
p < 1/12
Correctie: p = 0 moeten we uitsluiten aangezien we dan geen vierkantsvergelijking meer hebben en de afgeleide dan slechts één nulpunt heeft. Zie hieronder.
[ Bericht 0% gewijzigd door Riparius op 13-07-2012 00:25:04 ]
Dat, of de vwo B examens zijn te makkelijk, daar draai ik mijn hand niet voor om.quote:
Als je dit niet kunt moet je je ernstig afvragen of die studie wel geschikt voor je is. Het zijn niet voor niets toelatingsexamens.
En bedankt, nu ziet het er inderdaad erg simpel uit.
De examens misschien, maar als ze alle stof willen behandelen kunnen ze moeilijk alles vragen binnen 3 uur he. Als het goed is zou je met wiskunde B vaardigheden deze opgave op kunnen lossen. Ik zag hem in ieder geval wél.quote:
[..]
Dat, of de vwo B examens zijn te makkelijk, daar draai ik mijn hand niet voor om.
En bedankt, nu ziet het er inderdaad erg simpel uit.
Ik had er niet aan gedacht om de discriminant in te zetten, misschien mis ik een beetje creativiteit..
Wel jammer dat zowel de EUR als Riparius het antwoord fout hebben.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
uhh?quote:Op donderdag 12 juli 2012 21:19 schreef GlowMouse het volgende:
Wel jammer dat zowel de EUR als Riparius het antwoord fout hebben.
Dat je precies twee punten hebt waar de afgeleide nul is, betekent nog niet dat je ook precies twee extrema hebt.quote:
je hebt gelijk maar het antwoord en de uitwerking zijn twee verschillende dingenquote:
[..]
Dat je precies twee punten hebt waar de afgeleide nul is, betekent nog niet dat je ook precies twee extrema hebt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Je hebt gelijk, in die zin dat we ook naar de tweede afgeleide moeten kijken.quote:
[..]
Dat je precies twee punten hebt waar de afgeleide nul is, betekent nog niet dat je ook precies twee extrema hebt.
Uiteraard mag de tweede afgeleide niet gelijk zijn aan nul voor die waarden van x waarvoor geldt dat f'(x) = 0, anders heb je mogelijk geen extremum. Je moet dus inderdaad ook naar de tweede afgeleide kijken. De eerste afgeleide is gelijk aan nul indien 3px2 - 2x + 4 = 0. Het is mogelijk om te laten zien (dat mag tfors even doen) dat de tweede afgeleide dan alleen nul kan zijn indien 6px - 2 = 0 en dus x = 2/(6p). Maar dat is alleen het geval indien D = 4 - 48p = 0 terwijl voor p < 1/12 nu juist geldt D > 0. De situatie dat zowel de eerste als de tweede afgeleide gelijktijdig nul zijn doet zich dus niet voor zodat er voor p < 1/12 (edit: en tevens p ≠ 0) inderdaad altijd twee extremen zijn.
[ Bericht 1% gewijzigd door Riparius op 14-07-2012 12:33:23 ]
Dat is het niet, denk nog maar even naquote:
[..]
Je hebt gelijk, maar het antwoord is wel degelijk correct.
Thabit ziet ook direct dat het niet klopt, die zag het bij iets vergelijkbaars eerder ook.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dit is niet per definitie zo, het behoort wel tot de mogelijkheden. (Bij bijvoorbeeld f(x) = x4 heb je f''(0) = 0, maar x = 0 is toch een minimum). Maargoed, voor je argument maakt dat niet uit, en je zei al dat je niet echt fris meer bent.quote:
[..]
Je hebt gelijk, in die zin dat we ook nar de tweede afgeleide moeten kijken.
Uiteraard mag de tweede afgeleide niet gelijk zijn aan nul voor die waarden van x waarvoor geldt dat f'(x) = 0, anders heb je geen extremum.
/mierenneuken
Je hebt gelijk, als f'(x) = 0 en tevens f''(x) = 0 dan moet je inderdaad naar hogere afgeleiden gaan kijken. Mijn argument was hier om te laten zien dat de tweede afgeleide in ieder geval niet gelijk is aan nul voor die waarden van x waarvoor de eerste afgeleide gelijk is aan nul, en dat is voldoende om te besluiten dat je een extremum hebt.quote:
[..]
Dit is niet per definitie zo, het behoort wel tot de mogelijkheden. (Bij bijvoorbeeld f(x) = x4 heb je f''(0) = 0, maar x = 0 is toch een minimum). Maargoed, voor je argument maakt dat niet uit, en je zei al dat je niet echt fris meer bent.
/mierenneuken
Maar goed, ik heb zwaar getafeld en wat gedronken, en dan kan ik beter niet hier nog gaan posten, dat blijkt wel. Dus ik stop er nu mee en ga maar eens op tijd naar bed.
Valt me tegen Thenxero. Uit het gegeven dat mensen fouten maken volgt uiteraard niet direct dat iemand die een fout maakt ook een mens is, ofwel de omgekeerde stelling klopt niet.
In mijn axiomatisch stelsel stond dat Riparius ofwel een wiskundemachine was of een mens. Daarom geldt de stelling: als Riparius een fout maakt, dan is hij een mens.
Ik heb een vraag over de formule van Taylor.
Definieer
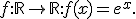
Er geldt voor f met Taylor dat
![\exists c \in [0,x]:e^x=\sum^{n}_{k=0} \frac{x^k}{k!}+\frac{e^c}{(n+1)!} x^{n+1}.](https://forum.fok.nl/lib/mimetex.cgi?%5Cexists%20c%20%5Cin%20%5B0%2Cx%5D%3Ae%5Ex%3D%5Csum%5E%7Bn%7D_%7Bk%3D0%7D%20%5Cfrac%7Bx%5Ek%7D%7Bk%21%7D%2B%5Cfrac%7Be%5Ec%7D%7B%28n%2B1%29%21%7D%20x%5E%7Bn%2B1%7D.)
De functie f blijft zichzelf na n+2 keer te differentiëren naar x. De rechterlid wordt nul. Mijn vraag is: waar gaat het mis in deze redenering?
Definieer
Er geldt voor f met Taylor dat
De functie f blijft zichzelf na n+2 keer te differentiëren naar x. De rechterlid wordt nul. Mijn vraag is: waar gaat het mis in deze redenering?
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
c is niet constant, maar hangt van x af.quote:
Ik heb een vraag over de formule van Taylor.
Definieer
Er geldt voor f met Taylor dat
De functie f blijft zichzelf na n+2 keer te differentiëren naar x. De rechterlid wordt nul. Mijn vraag is: waar gaat het mis in deze redenering?
Inderdaad. Dankje Thabit!quote:
[..]
c is niet constant, maar hangt van x af.
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Spreekt voor zich, als je met 3px2 - 2x + 4 de extremen van f(x) kunt berekenen, dan kun je met de afgeleide daar weer van berekenen of een veronderstelde extreme misschien een buigpunt van f(x) is. Maar bedankt!quote:
[..]
Je hebt gelijk, in die zin dat we ook naar de tweede afgeleide moeten kijken.
Uiteraard mag de tweede afgeleide niet gelijk zijn aan nul voor die waarden van x waarvoor geldt dat f'(x) = 0, anders heb je mogelijk geen extremum. Je moet dus inderdaad ook naar de tweede afgeleide kijken. De eerste afgeleide is gelijk aan nul indien 3px2 - 2x + 4 = 0. Het is mogelijk om te laten zien (dat mag tfors even doen) dat de tweede afgeleide dan alleen nul kan zijn indien 6px - 2 = 0 en dus x = 2/(6p). Maar dat is alleen het geval indien D = 4 - 48p = 0 terwijl voor p < 1/12 nu juist geldt D > 0. De situatie dat zowel de eerste als de tweede afgeleide gelijktijdig nul zijn doet zich dus niet voor zodat er voor p < 1/12 (edit: en tevens p ≠ 0) inderdaad altijd twee extremen zijn.
Ik heb behalve wis B weinig ervaring met wiskunde en ga gewoon door met oefenen. Ik hoop zo beetje bij beetje er achter te komen hoe je efficiënt dingen oplost. Begin er bijvoorbeeld achter te komen dat het handig is om van te voren een soort van "als dit, dan dat" schema te maken. In de zin van, eerst een planning maken met verschillende manieren waarop het opgelost kan worden, en dan het rijtje af.. Het lijkt me dat een goede beheersing van wiskunde je zo ook helpt op andere gebieden.
ps. ik ga dat boek mathematical proofs hiervoor doornemen, weet iemand waar ik dat het goedkoopst kan vinden?
Weet iemand hoe ik het beste een bootstrap (trekken uit distributie) kan doen van een empirische tijdreeks in matlab, zodat ik iig. m'n 4 momenten behoud? Heb bijv. wel de built in functie van matlab gebruikt (bootstrp) maar het verkloot m'n kurtosis waardes op 1 of andere manier.
Krijg ik bijv. 10000 tijdreeksen waar m'n kurtosis varieert van -2 tot -1. Iemand ideetje?
Krijg ik bijv. 10000 tijdreeksen waar m'n kurtosis varieert van -2 tot -1
. Iemand ideetje?
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.
Ik kijk meestal op bol.com en amazon.com, of die echt het goedkoopst zijn weet ik niet, maar in ieder geval goedkoper dan de meeste winkels, en je kan bijna alles daar wel vinden.quote:
ps. ik ga dat boek mathematical proofs hiervoor doornemen, weet iemand waar ik dat het goedkoopst kan vinden?
Waarom wil je dat boek doornemen voor econometrie?quote:
ps. ik ga dat boek mathematical proofs hiervoor doornemen, weet iemand waar ik dat het goedkoopst kan vinden?
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Ik weet nog niet of ik econometrie of iets anders wil gaan studeren. Wat ik wil bereiken met dat boek is het volgende: Dat ik oefen om wiskundige problemen (in het algemeen, die ook bij andere studies behalve econometrie voorkomen) efficiënter op te lossen. Dat achteraf simpele sommetje dat ik een paar pagina´s terug in deze discussie niet kon oplossen had ik wel kunnen oplossen als ik iets planmatiger had gedacht (hoop ik).
Wat zou jij aanraden dan?
Wat zou jij aanraden dan?
Ik kan opzicht niet veel aanraden. Dat boek kan werken, maar het kan ook niet werken. Je moet sowieso meer tijd eraan besteden dan even doornemen van een boek.quote:
Ik weet nog niet of ik econometrie of iets anders wil gaan studeren. Wat ik wil bereiken met dat boek is het volgende: Dat ik oefen om wiskundige problemen (in het algemeen, die ook bij andere studies behalve econometrie voorkomen) efficiënter op te lossen. Dat achteraf simpele sommetje dat ik een paar pagina´s terug in deze discussie niet kon oplossen had ik wel kunnen oplossen als ik iets planmatiger had gedacht (hoop ik).
Wat zou jij aanraden dan?
Merk wel op dat dat boek echt gericht is om het denken over wiskunde als een middelbare scholier om te zetten naar het denken als een theoretische wiskundige. Dus je moet niet denken dat in dat boek afleiden of integreren van functies behandeld wordt, maar het rigoureus definiëren van wiskundige objecten en bewijzen van wiskundige stellingen.
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Voorstel. Zou het niet interessant zijn als we standaard in de OP een uitgebreide lijst opnemen van goede wiskundeboeken waar geen copyright op zit (mag ook zeker Engelstalig zijn! Of Duitstalig of Franstalig), goede dictaten (bijv. van de Universiteit Leiden of een paar dictaten van Jan van de Craats) en links naar goede websites waar je veel over wiskunde kan leren? Of misschien een andere draad hiervoor aanmaken, sluiten (de moderators kunnen wijzigingen aanbrengen) en deze stickyen? Ook voor natuurkunde lijkt me dat een leuk idee. Er zijn parels van boeken die je gewoon gratis mag downloaden. In het geval van Engelstalige boeken heb je zelfs amper in de gaten dat het een oud boek is wanneer het rond 1900 is geschreven.
Ik weet dat hier wat mensen zijn die een interessant lijstje kunnen samenstellen dus laten we dat eens doen.
Ik weet dat hier wat mensen zijn die een interessant lijstje kunnen samenstellen dus laten we dat eens doen.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Ik heb veel interesse in dat boek Mathematical Proofs, juist omdat er zo weinig boeken zijn die zijn gericht op de transitie van iets simpels als calculus naar meer theoretische wiskunde.
Helaas is dat boek niet te downloaden. Misschien dat ik het toch wel wil kopen maar kennen jullie soortgelijke boeken die wat gemakkelijker te krijgen zijn?
Helaas is dat boek niet te downloaden. Misschien dat ik het toch wel wil kopen maar kennen jullie soortgelijke boeken die wat gemakkelijker te krijgen zijn?
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Lijkt me een prima planquote:
Voorstel. Zou het niet interessant zijn als we standaard in de OP een uitgebreide lijst opnemen van goede wiskundeboeken waar geen copyright op zit (mag ook zeker Engelstalig zijn!
Er is inderdaad veel leuks te downloaden.
Waar haal je die vandaan?quote:
poeh, die entrance examination mathematics level 3 for econometrics sample questions van de EUR is wel een niveautje hoger dan vwo wiskunde B, voor mij tenminste.
ik kom er weer niet uit bij vraag 3b, geen idee waar te beginnen eigenlijk:
f(x) = e^(4x-x^2+px^3)
Determine all values of p for which f(x) has exactly two extremes. Het antwoord is trouwens p < 1/12.
Ik dacht dat ik wel goed was in wiskunde, VWO wiskunde B is een makkie voor mij, maar misschien toch niet dan ;-)
Op tenen trappen is wel je specialiteit he, haha.quote:Op donderdag 12 juli 2012 23:47 schreef GlowMouse het volgende:
Het moge duidelijk zijn dat je beter niet aan de EUR kunt studeren.
Dat is niet heel makkelijk te vinden: ga naar
http://www.eur.nl/ese/eng(...)gramme/how_to_apply/
en klik dan op 1. Online mathematics entrance exam at your home institution , dan komen ze te voor schijn ;-)
http://www.eur.nl/ese/eng(...)gramme/how_to_apply/
en klik dan op 1. Online mathematics entrance exam at your home institution , dan komen ze te voor schijn ;-)
Zoals ik al zei, als ik van deze toets terug ga naar een oefenexamen wisB, dan lijkt het laatste toch voor een klas lager. Dus gelukkig dat ik deze tegen ben gekomen, het heeft me er gelijk op gewezen dat ik ipv op de automatische piloot toch wat meer vaardigheden moet ontwikkelen om afwijkende vraagstukken soepel op te lossen.
Moet je die teller zien rechts op die pagina.quote:
Dat is niet heel makkelijk te vinden: ga naar
http://www.eur.nl/ese/eng(...)gramme/how_to_apply/
en klik dan op 1. Online mathematics entrance exam at your home institution , dan komen ze te voor schijn ;-)
Wat is hier 'afwijkend' aan? Misschien moet je eerst deze eens proberen. Zijn wat eenvoudiger.quote:
Zoals ik al zei, als ik van deze toets terug ga naar een oefenexamen wisB, dan lijkt het laatste toch voor een klas lager. Dus gelukkig dat ik deze tegen ben gekomen, het heeft me er gelijk op gewezen dat ik ipv op de automatische piloot toch wat meer vaardigheden moet ontwikkelen om afwijkende vraagstukken soepel op te lossen.
Wel bijzonder klachtwaardig ja.quote:
[..]
Moet je die teller zien rechts op die pagina.
