SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Snelle vraag,
sin (2/3) pi
Omdat mijn rekenmachinetje geen radialen pikt maar graden,
(2/3) * 180 = 120
sin 120 = 0,87
Het boek geeft het antwoord (1/2) * sqrt(3)
Ik zie dat het hetzelfde is, maar hoe komen zij daar?
sin (2/3) pi
Omdat mijn rekenmachinetje geen radialen pikt maar graden,
(2/3) * 180 = 120
sin 120 = 0,87
Het boek geeft het antwoord (1/2) * sqrt(3)
Ik zie dat het hetzelfde is, maar hoe komen zij daar?
"Social order at the expense of liberty is hardly a bargain."
Middelbare school denk ik?
Dat riedeltje moesten wij uit ons hoofd leren. Is makkelijk te onthouden en als je een globaal beeld hebt hoe een (co)sinus eruit ziet al helemaal.
Dat riedeltje moesten wij uit ons hoofd leren. Is makkelijk te onthouden en als je een globaal beeld hebt hoe een (co)sinus eruit ziet al helemaal.
gr gr
En als je het even kwijt bent, kan je altijd een gelijkzijdige driehoek (voor de sinus en cosinus van 60 graden, of π/3 radialen) of een half vierkant dat is afgesneden via de diagonaal (voor de sinus en cosinus van 45 graden of π/2).quote:Op maandag 4 juni 2012 17:20 schreef Quyxz_ het volgende:
Middelbare school denk ik?
[ afbeelding ]
Dat riedeltje moesten wij uit ons hoofd leren. Is makkelijk te onthouden en als je een globaal beeld hebt hoe een (co)sinus eruit ziet al helemaal.
Helaas weet ik niet zo snel een driehoek waarmee je de sinus en cosinus van π/6 kan vinden. Het zou kunnen met de somformule voor de sinus/cosinus, maar dan moet je de somformule onthouden ipv sin(π/6)=1/4, wat me niet echt makkelijker lijkt
[ Bericht 8% gewijzigd door kutkloon7 op 04-06-2012 17:43:19 ]
Je kunt dit eenvoudig meetkundig beredeneren. Teken een gelijkzijdige driehoek ABC, de hoeken van deze driehoek zijn dan elk 60 graden. Teken vanuit (bijvoorbeeld) hoekpunt C een hoogtelijn, het voetpunt D van deze hoogtelijn is dan het midden van zijde AB. Nu is driehoek ACD rechthoekig, en aangezien D het midden is van AB en dus AD = ½∙AB en ook AB = AC hebben we dus:quote:Op maandag 4 juni 2012 17:15 schreef Quir het volgende:
Snelle vraag,
sin (2/3) pi
Omdat mijn rekenmachinetje geen radialen pikt maar graden,
(2/3) * 180 = 120
sin 120 = 0,87
Het boek geeft het antwoord (1/2) * sqrt(3)
Ik zie dat het hetzelfde is, maar hoe komen zij daar?
AD = ½∙AC
En volgens Pythagoras hebben we ook:
AC2 = AD2 + CD2
En dus:
CD2 = AC2 - AD2 = AC2 - (½∙AC)2 = AC2 - ¼∙AC2 = ¾∙AC2
En dus:
CD = √(¾)∙AC = ½√3∙AC
Nu is in een rechthoekige driehoek de sinus van een scherpe hoek de verhouding tussen de overstaande rechthoekszijde en de schuine zijde, dus hebben we:
sin 60° = sin ∠DAC = CD : AC = ½√3∙AC : AC = ½√3
En aangezien supplementaire hoeken dezelfde sinus hebben, hebben we dus ook
sin 120° = sin(180° - 60°) = sin 60° = ½√3
Heel eenvoudig: als je een rechthoekige driehoek hebt met een hoek van 60 graden, dan is de andere scherpe hoek 30 graden. En uiteraard is de cosinus van een hoek de sinus van het complement, daarom heet het ook een cosinus (als afkorting van complementi sinus).quote:
[..]
En als je het even kwijt bent, kan je altijd een gelijkzijdige driehoek (voor de sinus en cosinus van 60 graden, of π/3 radialen) of een half vierkant dat is afgesneden via de diagonaal (voor de sinus en cosinus van 45 graden of π/2).
Helaas weet ik niet zo snel een driehoek waarmee je de sinus en cosinus van π/6 kan vinden.
Ik begrijp dit alles, maar was meer uit naar een effectieve manier om zonder rekenmachine te berekenen. Ik heb pythagoras gebruikt, logischerwijs, maar op een iets andere manier.
cos˛ [a] + sin˛ [a] = 1
Eenheidscirkel naar concept
x˛ + y˛ = 1
Levert getallen op die moeilijker zijn om mee te rekenen.
cos˛ [a] + sin˛ [a] = 1
Eenheidscirkel naar concept
x˛ + y˛ = 1
Levert getallen op die moeilijker zijn om mee te rekenen.
Basisboek Wiskunde, dus, in principe, ja.quote:
Middelbare school denk ik?
[ afbeelding ]
Dat riedeltje moesten wij uit ons hoofd leren. Is makkelijk te onthouden en als je een globaal beeld hebt hoe een (co)sinus eruit ziet al helemaal.
"Social order at the expense of liberty is hardly a bargain."
Voor ik het vergeet, dit was wat ik moest hebben, dus.quote:Op maandag 4 juni 2012 18:06 schreef Riparius het volgende:
[..]
Je kunt dit eenvoudig meetkundig beredeneren. Teken een gelijkzijdige driehoek ABC, de hoeken van deze driehoek zijn dan elk 60 graden. Teken vanuit (bijvoorbeeld) hoekpunt C een hoogtelijn, het voetpunt D van deze hoogtelijn is dan het midden van zijde AB. Nu is driehoek ACD rechthoekig, en aangezien D het midden is van AB en dus AD = ½∙AB en ook AB = AC hebben we dus:
AD = ½∙AC
En volgens Pythagoras hebben we ook:
AC2 = AD2 + CD2
En dus:
CD2 = AC2 - AD2 = AC2 - (½∙AC)2 = AC2 - ¼∙AC2 = ¾∙AC2
En dus:
CD = √(¾)∙AC = ½√3∙AC
Nu is in een rechthoekige driehoek de sinus van een scherpe hoek de verhouding tussen de overstaande rechthoekszijde en de schuine zijde, dus hebben we:
sin 60° = sin ∠DAC = CD : AC = ½√3∙AC : AC = ½√3
En aangezien supplementaire hoeken dezelfde sinus hebben, hebben we dus ook
sin 120° = sin(180° - 60°) = sin 60° = ½√3
Dank allen.
"Social order at the expense of liberty is hardly a bargain."
Riparius, nu je er toch bent.
Ik had vandaag wiskunde, zoals een echte baas, en ik was wat mee aan het lezen bij de discussie over conflictlijnen (ellips).
Nu zei mijn wiskundedocent dat een ellips juist de conflictlijn (stelling / definitie doet er in deze vraag even niet toe) is van een cirkel binnen een grotere cirkel. Door middel van een cirkel met straal r1 + r2 te tekenen kreeg je dus een "somcirkel". Aan de hand van deze cirkel was het mogelijk om de ellips te construeren (en te bewijzen, aangezien de afstand van beide brandpunten N en M tot de ellips opgeteld een constante vormen, namelijk de straal van de "somcirkel").
Maar is dan de conflictlijn van een punt binnen een cirkel ook een ellips, en zoja, hoe construeer ik deze?
Ik had vandaag wiskunde, zoals een echte baas, en ik was wat mee aan het lezen bij de discussie over conflictlijnen (ellips).
Nu zei mijn wiskundedocent dat een ellips juist de conflictlijn (stelling / definitie doet er in deze vraag even niet toe) is van een cirkel binnen een grotere cirkel. Door middel van een cirkel met straal r1 + r2 te tekenen kreeg je dus een "somcirkel". Aan de hand van deze cirkel was het mogelijk om de ellips te construeren (en te bewijzen, aangezien de afstand van beide brandpunten N en M tot de ellips opgeteld een constante vormen, namelijk de straal van de "somcirkel").
Maar is dan de conflictlijn van een punt binnen een cirkel ook een ellips, en zoja, hoe construeer ik deze?
Hoe bedoel je moeilijker? Je hebt (½)2 + (½∙√3)2 = 1.quote:Op maandag 4 juni 2012 18:54 schreef Quir het volgende:
Ik begrijp dit alles, maar was meer uit naar een effectieve manier om zonder rekenmachine te berekenen. Ik heb pythagoras gebruikt, logischerwijs, maar op een iets andere manier.
cos˛ [a] + sin˛ [a] = 1
Eenheidscirkel naar concept
x˛ + y˛ = 1
Levert getallen op die moeilijker zijn om mee te rekenen.
Het wordt pas lastig als je bijvoorbeeld wil afleiden dat sin 18° = ¼(√5 - 1).
Logicaquote:
Natuurlijk, punt is een cirkel met straal 0 immers.
k*t
Beiden zijn dan nog niet bekend, wat maaktquote:
[..]
Hoe bedoel je moeilijker? Je hebt (½)2 + (½∙√3)2 = 1.
Het wordt pas lastig als je bijvoorbeeld wil afleiden dat sin 18° = ¼(√5 - 1).
cos [a] = √( 1 - (4/9) * pi˛ )
"Social order at the expense of liberty is hardly a bargain."
Dit wordt allemaal duidelijk als je het PDF bestand van Dick Klingens waarnaar ik hierboven verwijs bestudeert. Hij bespreekt ook de conflictlijn van twee cirkels.quote:
Riparius, nu je er toch bent.
Ik had vandaag wiskunde, zoals een echte baas, en ik was wat mee aan het lezen bij de discussie over conflictlijnen (ellips).
Nu zei mijn wiskundedocent dat een ellips juist de conflictlijn (stelling / definitie doet er in deze vraag even niet toe) is van een cirkel binnen een grotere cirkel. Door middel van een cirkel met straal r1 + r2 te tekenen kreeg je dus een "somcirkel". Aan de hand van deze cirkel was het mogelijk om de ellips te construeren (en te bewijzen, aangezien de afstand van beide brandpunten N en M tot de ellips opgeteld een constante vormen, namelijk de straal van de "somcirkel").
Maar is dan de conflictlijn van een punt binnen een cirkel ook een ellips, en zoja, hoe construeer ik deze?
Overigens, als je toe bent aan een nieuwe uitdaging, dan heb ik nog wel een (algebra)opgave voor je uit de oude doos. Eentje die goede H.B.S. B en Gymnasium β leerlingen uit de hogere klassen ruim een halve eeuw geleden nog konden oplossen.
Misschien moet je een niet-complex voorbeeld bedenken als je dan toch leuk wilt zijn..quote:Op maandag 4 juni 2012 19:12 schreef Quir het volgende:
[..]
Beiden zijn dan nog niet bekend, wat maakt
cos [a] = √( 1 - (4/9) * pi˛ )
quote:
[..]
Dit wordt allemaal duidelijk als je het PDF bestand van Dick Klingens waarnaar ik hierboven verwijs bestudeert. Hij bespreekt ook de conflictlijn van twee cirkels.
Overigens, als je toe bent aan een nieuwe uitdaging, dan heb ik nog wel een (algebra)opgave voor je uit de oude doos. Eentje die goede H.B.S. B en Gymnasium β leerlingen uit de hogere klassen ruim een halve eeuw geleden nog konden oplossen.
Kom maar op.
Ik was vandaag nog op zoek naar de oude vwo wiskunde B1,2 boeken (Boek 6 boeide me, daarin stonden de betreffende conflictlijnen beschreven.) Maar John zou hem morgen meenemen, als hij het niet vergeet. (John is mijn docent wiskunde B&D)[ Bericht 3% gewijzigd door #ANONIEM op 04-06-2012 19:20:51 ]
Ik denk dat je een beetje in de war bent ...quote:
[..]
Beiden zijn dan nog niet bekend, wat maakt
cos [a] = √( 1 - (4/9) * pi˛ )
Nog even over die conflictlijnen: die zijn geďntroduceerd door het Freudenthalinstituut. Op hun website kun je wel wat concept leerstofmodules inzien (link: 1 2). Ik ben er zelf niet enthousiast over, maar dat was denk ik al duidelijk.quote:
[..]
Kom maar op.
Dat klopt. Want dat geeft een negatief getal. Daar kom ik nog op terug.quote:
[..]
Ik denk dat je een beetje in de war bent ...
"Social order at the expense of liberty is hardly a bargain."
Wat heb je dan liever? Dat mensen het kegelsneden gaan noemen en vervolgens nooit weten waar het voor dient?quote:
[..]
Nog even over die conflictlijnen: die zijn geďntroduceerd door het Freudenthalinstituut. Op hun website kun je wel wat concept leerstofmodules inzien (link: 1 2). Ik ben er zelf niet enthousiast over, maar dat was denk ik al duidelijk.
Het is dat ik de methode ken om eenvoudige identiteiten te vinden voor Sin(nx), anders zou het inderdaad een hell of a job zijn.quote:
[..]
Hoe bedoel je moeilijker? Je hebt (˝)2 + (˝∙√3)2 = 1.
Het wordt pas lastig als je bijvoorbeeld wil afleiden dat sin 18° = Ľ(√5 - 1).
Goed. Bedenk dat er destijds nog geen elektronische rekenhulpmiddelen beschikbaar waren. Het is dus mogelijk - en ook de bedoeling - de volgende opgave uitsluitend met gebruikmaking van pen en papier op te lossen. Als je een oplossing post, laat dan ook zien hoe je aan je oplossing bent gekomen. Hier is de opgave:quote:
In een plat vlak met een cartesisch assenstelsel ligt een rechte lijn die door het punt (1;1) gaat. Deze lijn snijdt de positieve x-as en de positieve y-as. De onderlinge afstand van de snijpunten bedraagt 4 eenheden en het snijpunt met de x-as ligt dichter bij de oorsprong dan het snijpunt met de y-as. Bereken de exacte coördinaten van de snijpunten van de lijn met de beide assen.
Begrepen!
Geen passer & geodriehoek/liniaal?
[ Bericht 83% gewijzigd door #ANONIEM op 04-06-2012 19:33:09 ]
Geen passer & geodriehoek/liniaal?
[ Bericht 83% gewijzigd door #ANONIEM op 04-06-2012 19:33:09 ]
Het hele woord kegelsnede komt in de conceptmodules van het Freudenthalinstituut niet voor en dat is om te beginnen al een grote misser, zeker omdat ze Apollonius wél noemen. Als leerlingen dan een vervolgopleiding gaan doen en ze lezen in een engels boek de term conic sections, dat zou het dus zo maar kunnen dat ze niet eens begrijpen waar het over gaat. Overigens komt in de Nederlandse versie van Cabri waar de samenstellers nogal mee dwepen dan weer wel het woord kegelsneden voor.quote:
[..]
Wat heb je dan liever? Dat mensen het kegelsneden gaan noemen en vervolgens nooit weten waar het voor dient?
Tuurlijk mag je voor jezelf een tekening maken, is ook aanbevolen. Maar zoals gezegd, gevraagd wordt een exact antwoord.quote:
Begrepen!
Geen passer & geodriehoek/liniaal?
Gewoon een assenstelsel getekend, met een geodriehoek beetje uitgemeten. En nu de voorwaarden en vergelijkingen opstellen, en dan zien waar het schip strandt. Ik heb al een klein ideetje.quote:
[..]
Tuurlijk mag je voor jezelf een tekening maken, is ook aanbevolen. Maar zoals gezegd, gevraagd wordt een exact antwoord.
Ach, ik kan 't niet meer terugvinden in m'n kladderschrift. Zal wel hebben lopen spiegelen.quote:Op maandag 4 juni 2012 19:24 schreef Quir het volgende:
[..]
Dat klopt. Want dat geeft een negatief getal. Daar kom ik nog op terug.
Heb er nu in ieder geval bovenstaande wijze in staan.
"Social order at the expense of liberty is hardly a bargain."
Toch niet weer een derde/vierdegraadspolynoom die je mag oplossen?quote:
[..]
Goed. Bedenk dat er destijds nog geen elektronische rekenhulpmiddelen beschikbaar waren. Het is dus mogelijk - en ook de bedoeling - de volgende opgave uitsluitend met gebruikmaking van pen en papier op te lossen. Als je een oplossing post, laat dan ook zien hoe je aan je oplossing bent gekomen. Hier is de opgave:
In een plat vlak met een cartesisch assenstelsel ligt een rechte lijn die door het punt (1;1) gaat. Deze lijn snijdt de positieve x-as en de positieve y-as. De onderlinge afstand van de snijpunten bedraagt 4 eenheden en het snijpunt met de x-as ligt dichter bij de oorsprong dan het snijpunt met de y-as. Bereken de exacte coördinaten van de snijpunten van de lijn met de beide assen.
Het komt neer op het snijpunt bepalen van een cirkel en een hyperbool. Altijd leuk ja..quote:
[..]
Toch niet weer een derde/vierdegraadspolynoom die je mag oplossen?
Ja, je moet het stelselquote:
[..]
Het komt neer op het snijpunt bepalen van een cirkel en een hyperbool. Altijd leuk ja..
a^2+b^2 = 16
a=b/(b-1)
oplossen. (en als ik dat omschrijf krijg ik een vierdegraadsvergelijking
)[ Bericht 12% gewijzigd door thenxero op 04-06-2012 20:27:09 ]
Hah, ik had het even snel uit mijn hoofd opschreven, stom dat ik het niet zag.quote:
[..]
Heel eenvoudig: als je een rechthoekige driehoek hebt met een hoek van 60 graden, dan is de andere scherpe hoek 30 graden. En uiteraard is de cosinus van een hoek de sinus van het complement, daarom heet het ook een cosinus (als afkorting van complementi sinus).
Hoe kom je bij die a=b/(b-1)? Ik weet niets over hyperbolen verder.quote:
[..]
Ja, je moet het stelsel
a^2+b^2 = 16
a=b/(b-1)
oplossen.
Ik noem de gezochte x-coördinaat a, en de gezochte y-coördinaat b. Dan geldt dat ab/2 de oppervlakte is van de driehoek ingesloten door de x en y as en de gezochte lijn. Maar de oppervlakte is ook op een andere manier uit te drukken, namelijk: (a-1)(b-1)/2 + 1.quote:Op maandag 4 juni 2012 20:26 schreef Amoeba het volgende:
[..]
Hoe kom je bij die a=b/(b-1)? Ik weet niets over hyperbolen verder.
Dus (a-1)(b-1)/2 + 1 = ab/2. En dan oplossen voor a geeft a=b/(b-1).
Kun je dit toelichten?quote:
[..]
Ik noem de gezochte x-coördinaat a, en de gezochte y-coördinaat b. Dan geldt dat ab/2 de oppervlakte is van de driehoek ingesloten door de x en y as en de gezochte lijn. Maar de oppervlakte is ook op een andere manier uit te drukken, namelijk: (a-1)(b-1)/2 + 1.
Dus (a-1)(b-1)/2 + 1 = ab/2. En dan oplossen voor a geeft a=b/(b-1).
Dat is inderdaad het idee, maar mijn algebra klopt niet.quote:
Gewoon de driehoek splitsen in een vierkant en twee kleine driehoeken.
Krijg je die onzin a = ab-b
a = b(a-1)
a/(a-1) = b
zo kan het ook?
[ Bericht 55% gewijzigd door #ANONIEM op 04-06-2012 20:44:44 ]
a = b(a-1)
a/(a-1) = b
zo kan het ook?
[ Bericht 55% gewijzigd door #ANONIEM op 04-06-2012 20:44:44 ]
En dit geeftquote:
(a+b)/2 = ab/2
a+b = ab
b/a=b
Crap, ik kan niet meer helder denken
Dit gaat iig nergens heen.
26"
Fading slowly.
Fading slowly.
Je laatste regel klopt niet.quote:
[..]
En dit geeft
(a+b)/2 = ab/2
a+b = ab
b/a=b
Crap, ik kan niet meer helder denken
Dit gaat iig nergens heen.
Ik denk dat je zoiets moet doen.
a + b = ab
kwadrateren geeft
a˛ + b˛ + 2ab = a˛b˛
We weten
a˛+b˛=16
dus
16 + 2ab = a˛b˛
Substitueer ab=x. Dan krijgen we een kwadratische vergelijking in x:
x˛ - 2x - 16 = 0.
Met de ABC-formule kunnen we dan x oplossen. We weten dan dus de waarde van ab, want ab=x en x is bekend. Dus a=x/b. Maar omdat ook a+b=x, hebben we ook a=x-b. Dus x-b = x/b. Dus bx - b˛ = x. Dus dan hebben we een kwadratische vergelijking in b. Die kan je ook weer oplossen. Dan heb je dus b, en dan kan je ook a berekenen.
(De details laat ik over aan amoeba
)
a + b = ab
kwadrateren geeft
a˛ + b˛ + 2ab = a˛b˛
We weten
a˛+b˛=16
dus
16 + 2ab = a˛b˛
Substitueer ab=x. Dan krijgen we een kwadratische vergelijking in x:
x˛ - 2x - 16 = 0.
Met de ABC-formule kunnen we dan x oplossen. We weten dan dus de waarde van ab, want ab=x en x is bekend. Dus a=x/b. Maar omdat ook a+b=x, hebben we ook a=x-b. Dus x-b = x/b. Dus bx - b˛ = x. Dus dan hebben we een kwadratische vergelijking in b. Die kan je ook weer oplossen. Dan heb je dus b, en dan kan je ook a berekenen.
(De details laat ik over aan amoeba
)
Die hebben we dus nu:quote:
Het lijkt me dat het maken van de juiste vierdegraadsvergelijking niet het grootste probleem is.
a2 + b2 = 16
-a4 + 2a3 + 14a2 -32a + 16 = 0.
Ik heb morgen een proefwerk. Alleen ik snap niks van de discriminant.
Ik heb een som waar ik maar niet uit kan komen :S
f (x) = 2x˛ -4x & g(x) = x + 10.
En dan moet je ook nog afleiden of die de lijn snijdt, raakt of geen gemeenschappelijk punt heeft.
Wie o wie kan me helpen?
Alvast bedankt
Ik heb een som waar ik maar niet uit kan komen :S
f (x) = 2x˛ -4x & g(x) = x + 10.
En dan moet je ook nog afleiden of die de lijn snijdt, raakt of geen gemeenschappelijk punt heeft.
Wie o wie kan me helpen?
Alvast bedankt
Stel f(x) = g(x) en los op voor x met behulp van de abc-formule.quote:
Ik heb morgen een proefwerk. Alleen ik snap niks van de discriminant.
Ik heb een som waar ik maar niet uit kan komen :S
f (x) = 2x˛ -4x & g(x) = x + 10.
En dan moet je ook nog afleiden of die de lijn snijdt, raakt of geen gemeenschappelijk punt heeft.
Wie o wie kan me helpen?
Alvast bedankt
De discriminant is inderdaad 105. Laat maar zien hoe jij het berekent.quote:
thenxero.
ik heb het uitgerekend en kom op 55 uit maar in het antwoordenboekje staat 105.
Een lijn snijdt wanneer geldt:
f(x) = g(x) & f'(x)*g'(x) = -1
Een lijn raakt wanneer:
f(x) = g(x) & f'(x) = g'(x)
f(x) = g(x) & f'(x)*g'(x) = -1
Een lijn raakt wanneer:
f(x) = g(x) & f'(x) = g'(x)
Sorry. b = (-1-√17 +/- √(14-2√17))/2quote:
Amoeba, heb je b al berekend van het Riparius probleem?
ofzo?
Over die lijn door (1,1):
noem de hoek tussen de lijn en de x-as θ, noem x=cosθ en y=sinθ, dan moet
,
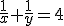dus
,
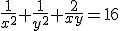dus
,
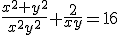dus
,
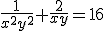dus
,
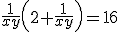substitutie z=1/(xy),
,
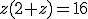geeft een oplossing p voor z en dus ook voor xy.
Vervolgens x=1/(yp) substitueren in
,
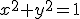geeft
,
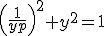dus
,
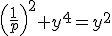substitutie z=y^2,
,
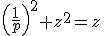geeft een oplossing q voor y,
vervolgens met Pythagoras het antwoord berekenen.
noem de hoek tussen de lijn en de x-as θ, noem x=cosθ en y=sinθ, dan moet
dus
dus
dus
dus
substitutie z=1/(xy),
geeft een oplossing p voor z en dus ook voor xy.
Vervolgens x=1/(yp) substitueren in
geeft
dus
substitutie z=y^2,
geeft een oplossing q voor y,
vervolgens met Pythagoras het antwoord berekenen.
b = (1+√17 +/- √(14-2√17))/2 krijg ik.quote:
[..]
Sorry. b = (-1-√17 +/- √(14-2√17))/2
ofzo?
Volgens mij hebben we dan
b = (1+√17 + √(14-2√17))/2
a = (1+√17 - √(14-2√17))/2
(want het probleem is symmetrisch in a en b en het was gegeven dat a<b)
-bx, mijn excuses. Je hebt gelijk.quote:
[..]
b = (1+√17 +/- √(14-2√17))/2 krijg ik.
Volgens mij hebben we dan
b = (1+√17 + √(14-2√17))/2
a = (1+√17 - √(14-2√17))/2
(want het probleem is symmetrisch in a en b en het was gegeven dat a<b)
Numeriek lijkt het ook allemaal te kloppen zo in wolfram alpha. Volgens mij is dit hem dus. Leuk probleempje.quote:
Waar ellipsen een mens wel niet toe brengen.quote:
[..]
Numeriek lijkt het ook allemaal te kloppen zo in wolfram alpha. Volgens mij is dit hem dus. Leuk probleempje.
