SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Sorry. Ik bedoelde naar links.quote:Op zaterdag 19 mei 2012 21:24 schreef GlowMouse het volgende:
Je krijgt 2x = pi - (pi/2 - 3x) + k*2pi, welke - gaat er naar rechts?
Dat is het natuurlijk... Wat stom dat ik dit niet zelf kon bedenken. Dank u!quote:
Je mag altijd beide leden met -1 vermenigvuldigen als je dat bedoelt
Je moet bedenken dat als je hebt:quote:
[..]
Sorry. Ik bedoelde naar links.
[..]
Dat is het natuurlijk... Wat stom dat ik dit niet zelf kon bedenken. Dank u!
sin α = sin β,
dat dan geldt:
α = β + 2kπ ∨α = (π - β) + 2kπ, k ∈ Z
Edit: ik zie dat je dat kennelijk al had bedacht.
Ik zie je post nu pas, leuke post welquote:
[..]
Is in het algemeen niet te doen, alleen in speciale gevallen. Dit soort kwadratische recursies spelen zelfs een belangrijke rol in de chaostheorie. Je kunt er ook fractals mee maken, zoals de Mandelbrotverzameling.
Een voorbeeld van eentje die nog wel te doen is (ik verklap de oplossing nog niet):
a1 = 1/3, an+1 = 2an2 - 1.
Ik moest eerlijk gezegd even op wolfram spieken voor de identiteit sin2 x - cos2 x = -2cos2 x, maar ik ben er uit geloof ik:
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Zonder die hint van Riparius weet ik niet of ik het zou snappen
[ Bericht 4% gewijzigd door kutkloon7 op 19-05-2012 22:47:59 ]
Vet dat dat met zo'n goniometrische substitutie kan. Ik had zo'n substitutie denk ik nooit zelf bedacht. 
Het kan eenvoudiger, daarom gaf ik kutkloon ook goniometrische identiteiten als hint.quote:
Vet dat dat met zo'n goniometrische substitutie kan. Ik had zo'n substitutie denk ik nooit zelf bedacht.
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
[ Bericht 0% gewijzigd door Riparius op 19-05-2012 23:19:36 ]
Dat is wel netjes ja. Maar ik gebruik die identiteiten te weinig om ze te kunnen onthouden, meer dan sin²+cos²=1 en wat spelen met sin en cos is niet zo vaak nodig
quote:
[..]
Het kan eenvoudiger, daarom gaf ik kutkloon ook goniometrische identiteiten als hint.Slim, ziet er een stuk minder mysterieus uitSPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
(Had ik maar even de moeite genomen om het als cosinus op te schrijven, ik had er nog aan gedacht)
[ Bericht 5% gewijzigd door kutkloon7 op 19-05-2012 23:24:46 ]
Zie je post nu pas, dank!quote:
[..]
De vergelijkingen die je geeft stellen in de driedimensionale ruimte vlakken voor, geen lijnen, dus hier gaat het al fout.
Het idee is dat je eerst een normaalvector n bepaalt van je vlak V. Dat is een vector die loodrecht op het vlak staat. Is nu v = (x,y,z) een willekeurige vector met eindpunt in je vlak V en v0 = (x0,y0,z0) een vaste vector met eindpunt in je vlak, dan is vector v - v0 evenwijdig aan je vlak en staat deze verschilvector dus loodrecht op je normaalvector n, zodat het inproduct van v- v0 en n gelijk is aan nul:
(1) n∙(v - v0) = 0
En dus geldt ook:
(2) n∙v = n∙v0
Een vaste vector v0 met eindpunt in je vlak V ken je al omdat je immers de drie punten A,B en C kent die in vlak V liggen, zodat je hier voor v0 bijvoorbeeld de vector a = (2,0,0) zou kunnen nemen zodat x0 =2, y0 = 0 en z0 = 0.
De kunst is nu om een geschikte normaalvector n = (a,b,c) te bepalen want dan kun je voor (1) schrijven:
(3) a(x - x0) + b(y - y0) + c(z - z0) = 0,
en voor (2) kun je schrijven:
(4) ax + by + cz = ax0 + by0 + cz0,
en (3) of (4) is uiteraard de gezochte cartesische vergelijking van je vlak. Om nu een geschikte normaalvector n = (a,b,c) en daarmee de waarden van a,b en c te vinden kun je bedenken dat n loodrecht staat op zowel de verschilvector b - a als de verschilvector c - a, aangezien deze beide verschilvectoren evenwijdig zijn aan vlak V. En dus moet het inproduct van n = (a,b,c) met zowel b - a = (-2,3,0) als c - a = (-2,0,4) gelijk zijn aan nul. Dit geeft:
(5a) -2a + 3b = 0
(5b) -2a + 4c = 0
Hier heb je twee lineaire vergelijkingen in drie onbekenden a, b en c, en dus lijkt het alsof je nog één lineaire vergelijking tekort komt. Maar dat is niet zo, want als we n met een scalar vermenigvuldigen, dan hebben we nog steeds een vector die loodrecht op vlak V staat, dus zijn a,b,c niet eenduidig bepaald. Dat is ook meteen duidelijk uit de cartesische vergelijking (3) want als je hier beide leden met een getal ongelijk nul vermenigvuldigt, dan heb je nog steeds een geldige cartesische vergelijking van je vlak V.
We kunnen nu met (5a) en (5b) de waarde van a en b uitdrukken in c. Uit (5b) volgt dat a = 2c en substitutie hiervan in (5a) levert b = (4/3)∙c en dus hebben we n = (2c, (4/3)∙c, c). Kiezen we nu bijvoorbeeld c = 3, dan krijgen we n = (6, 4, 3). Op grond van (3) wordt de cartesische vergelijking van je vlak V nu:
(6) 6(x - 2) + 4(y - 0) + 3(z - 0) = 0,
en uitwerken hiervan geeft:
(7) 6x + 4y + 3z = 12
Je kunt nu door invullen gemakkelijk controleren dat de coördinaten van de punten A, B en C inderdaad aan (7) voldoen. Overigens hadden we in dit speciale geval de vergelijking van het vlak direct uit het hoofd kunnen opschrijven in de vorm (1/2)∙x + (1/3)∙y + (1/4)∙z = 1 omdat van elk van de drie gegeven punten A resp. B resp. C alleen de x- resp. y- resp. z-coördinaat ongelijk is aan nul. Maar in het algemeen is dat uiteraard niet zo als je de cartesische vergelijking van een vlak door drie gegeven punten op moet stellen.
"Social order at the expense of liberty is hardly a bargain."
Ik heb nog wel een klassieker voor je (niet door mij bedacht dus) waar je eens je tanden in kunt zetten:quote:
Vet dat dat met zo'n goniometrische substitutie kan. Ik had zo'n substitutie denk ik nooit zelf bedacht.
We hebben een halve bol, waarvan we de straal voor het gemak gelijk aan één veronderstellen. Deze halve bol verdelen we nu door een vlak evenwijdig aan het deelvlak in twee delen met gelijke inhoud. Bereken de afstand van het deelvlak tot het middelpunt van de halve bol.
Gevraagd wordt een exacte uitdrukking voor de bedoelde afstand, dus geen numerieke benadering.
Nasty, ik dacht aan een simpele benadering, maar dan blijf ik hangen op de vergelijking h3-3h+1=0quote:
[..]
Ik heb nog wel een klassieker voor je (niet door mij bedacht dus) waar je eens je tanden in kunt zetten:
We hebben een halve bol, waarvan we de straal voor het gemak gelijk aan één veronderstellen. Deze halve bol verdelen we nu door een vlak evenwijdig aan het deelvlak in twee delen met gelijke inhoud. Bereken de afstand van het deelvlak tot het middelpunt van de halve bol.
Gevraagd wordt een exacte uitdrukking voor de bedoelde afstand, dus geen numerieke benadering.
Is het antwoord sin(1/3) ?quote:
[..]
Ik heb nog wel een klassieker voor je (niet door mij bedacht dus) waar je eens je tanden in kunt zetten:
We hebben een halve bol, waarvan we de straal voor het gemak gelijk aan één veronderstellen. Deze halve bol verdelen we nu door een vlak evenwijdig aan het deelvlak in twee delen met gelijke inhoud. Bereken de afstand van het deelvlak tot het middelpunt van de halve bol.
Gevraagd wordt een exacte uitdrukking voor de bedoelde afstand, dus geen numerieke benadering.
Staaltje primitiveren?
(Wentelen om de x-as?)
[ Bericht 43% gewijzigd door #ANONIEM op 20-05-2012 23:14:37 ]
(Wentelen om de x-as?)
[ Bericht 43% gewijzigd door #ANONIEM op 20-05-2012 23:14:37 ]
Ofwel wentelen om de x-as.
De inhoud van die halve bol is 2/3pi
Dus met behulp van primiteren berekenen voor welke x coordinaat dit 1/3pi is?
De inhoud van die halve bol is 2/3pi
Dus met behulp van primiteren berekenen voor welke x coordinaat dit 1/3pi is?
Ik kom uit op a3 -3a + 3 = 0quote:
[..]
Nasty, ik dacht aan een simpele benadering, maar dan blijf ik hangen op de vergelijking h3-3h+1=0
Wat doe ik fout?quote:
[..]
Die heeft als enige reële oplossing iets van -2...
De inhoud van een bol is 4/3pi. De inhoud van de halve bol met middelpunt M op de oorsprong (0 , 0). dus 2/3pi.
Dan neem ik de formule x2 + y2 = 1, druk x uit in y.
Dus x = wortel(1-y2)
Integraal van 0 tot a = 1/3 pi
Je moet de functie kwadrateren, dus die wortel valt mooi weg. De primitieve is dan toch x-1/3x3
Nou van 0 tot a. Blijft over:
a-1/3a3 = 1/3 (pi valt weg)
vermenigvuldigen met 3 en overhevelen naar een kant?
[ Bericht 0% gewijzigd door #ANONIEM op 20-05-2012 23:30:26 ]
Dit is de formule van een cilinder, niet van een bol.quote:
[..]
Wat doe ik fout?
De inhoud van een bol is 4/3pi. De inhoud van de halve bol met middelpunt M op de oorsprong (0 , 0). dus 2/3pi.
Dan neem ik de formule x2 + y2 = 1, druk x uit in y.
quote:Op zondag 20 mei 2012 23:33 schreef kutkloon7 het volgende:
[..]
Dit is de formule van een cilinder, niet van een bol.
Om exact te zijn. Dit is de formule van de eenheidscirkel, wat bij wentelen om de x-as een bol geeft.quote:
[..]
Dit is de formule van een cilinder, niet van een bol.
Nope. Ik geef de integraal. Ik ga uit van een tweedimensionale figuur die ik vervolgens om de x-as ga wentelen. Dit geeft dus de inhoud van een bol!quote:
[..]
Een bol is 3-dimensionaal, en je hebt nergens een z-coordinaat in je formule gebruikt.
Ah, ok. Dan begrijp ik gewoon niet helemaal wat je precies deedquote:
[..]
Om exact te zijn. Dit is de formule van de eenheidscirkel, wat bij wentelen om de x-as een bol geeft.
Dat kan je in principe exact oplossen (wel lelijk).quote:
Godverdomme, ik vermenigvuldig 2x met 3 bij c. Inderdaad, de vergelijking is x^3 - 3x + 1 = 0
En die heb ik nooit gehad. Zat wel even te kijken, maar ik heb nu staan:
m3 + n3 + 3mn(m+n) -3(m+n) + 1 = 0
Met x = m+n
en 3mn = 3 ofwel mn = 1
m3 + n3 + 3mn(m+n) -3(m+n) + 1 = 0
Met x = m+n
en 3mn = 3 ofwel mn = 1
Riparius, dan ga ik met de ABCD formule aan de gang.
Ik heb staan:
a3 -3a + 1 = 0
Grafisch geeft dit het juiste antwoord.
Nou goed, gaan we hier de ABCD formule op loslaten.
a = m+n
(m+n)3 -3(m+n) + 1 = 0
Dus
m3 + n3 + 3mn(m+n) -3(m+n) + 1 = 0
Dus 3mn = 3 ergo mn = 1
n = 1/m
Dus
m3 + 1/m3 + 1 = 0
Vermeningvuldigen met m3
m6 + m3 + 1 = 0
Substitutie naar q.
q = m3
q2 + q + 1 = 0
D = b2 -4ac
D = -3
Of moet ik hiermee verder rekenen..?
Ik heb staan:
a3 -3a + 1 = 0
Grafisch geeft dit het juiste antwoord.
Nou goed, gaan we hier de ABCD formule op loslaten.
a = m+n
(m+n)3 -3(m+n) + 1 = 0
Dus
m3 + n3 + 3mn(m+n) -3(m+n) + 1 = 0
Dus 3mn = 3 ergo mn = 1
n = 1/m
Dus
m3 + 1/m3 + 1 = 0
Vermeningvuldigen met m3
m6 + m3 + 1 = 0
Substitutie naar q.
q = m3
q2 + q + 1 = 0
D = b2 -4ac
D = -3
Of moet ik hiermee verder rekenen..?
Je bent zeker op de goede weg. Zoals inmiddels duidelijk is leidt het probleem tot een kubische vergelijking en die kun je in principe oplossen met de methode die aan Cardano wordt toegeschreven (maar niet van hem is), en dat is wat je hier ook doet. Maar nu loop je stuk op die negatieve discriminant ...quote:
Riparius, dan ga ik met de ABCD formule aan de gang.
Ik heb staan:
a3 -3a + 1 = 0
Grafisch geeft dit het juiste antwoord.
Nou goed, gaan we hier de ABCD formule op loslaten.
a = m+n
(m+n)3 -3(m+n) + 1 = 0
Dus
m3 + n3 + 3mn(m+n) -3(m+n) + 1 = 0
Dus 3mn = 3 ergo mn = 1
n = 1/m
Dus
m3 + 1/m3 + 1 = 0
Vermeningvuldigen met m3
m6 + m3 + 1 = 0
Substitutie naar q.
q = m3
q2 + q + 1 = 0
D = b2 -4ac
D = -3
Of moet ik hiermee verder rekenen..?
i*wortel 3. Ik ga verder.quote:
[..]
Je bent zeker op de goede weg. Zoals inmiddels duidelijk is leidt het probleem tot een kubische vergelijking en die kun je in principe oplossen met de methode die aan Cardano wordt toegeschreven (maar niet van hem is), en dat is wat je hier ook doet. Maar nu loop je stuk op die negatieve discriminant ...
Ik heb net CE Wiskunde B gehad, en het beginnetje van complexe getallen van Wiskunde D gehad. Het is geen ramp als me dit niet lukt.
ABCD formule wist ik enkel het bestaan van trouwens.
ABCD formule wist ik enkel het bestaan van trouwens.
Nougoed, dan heb ik q = -.5 ± .5 i rt 3
Als ik dan alles terugreken naar a kom ik uit op in beide gevallen uit op 1,53 (zegt mijn GR)
Ik zat nu wel op wolframalpha naar het definitieve antwoord te kijken, maar nee, geen idee hoe ze daaraan komen.
Ofwel:
Waar dit het antwoord was waar ik op uitkwam:
[ Bericht 25% gewijzigd door #ANONIEM op 21-05-2012 00:41:22 ]
Als ik dan alles terugreken naar a kom ik uit op in beide gevallen uit op 1,53 (zegt mijn GR)
Ik zat nu wel op wolframalpha naar het definitieve antwoord te kijken, maar nee, geen idee hoe ze daaraan komen.
Ofwel:
Waar dit het antwoord was waar ik op uitkwam:
[ Bericht 25% gewijzigd door #ANONIEM op 21-05-2012 00:41:22 ]
Ik snap trouwens niet waar het bij mij mis gaat. Ik probeerde bolcoördinaten toe te passen en dan bereken je dus
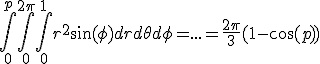
Dat moet gelijk zijn aan een kwart v/d inhoud van een bol, dus pi/3 .
Dus dan krijg je cos(p) = 1/2. Dus p=pi/3. Dat is dus de hoek t.o.v. het grondvlak. Dus sin(pi/3) = (hoogte van het snijvlak) / (straal (=1)) = hoogte van het snijvlak. Maar sin(pi/3)=0.8... veel te groot.
Dat moet gelijk zijn aan een kwart v/d inhoud van een bol, dus pi/3 .
Dus dan krijg je cos(p) = 1/2. Dus p=pi/3. Dat is dus de hoek t.o.v. het grondvlak. Dus sin(pi/3) = (hoogte van het snijvlak) / (straal (=1)) = hoogte van het snijvlak. Maar sin(pi/3)=0.8... veel te groot.
Tja, je GR zegt zoveel, maar de bedoeling was een exacte uitdrukking te geven, en het is toch duidelijk dat het antwoord reëel moet zijn en op het interval (0,1) moet liggen. Toch zit je best dichtbij.quote:
Nougoed, dan heb ik q = -.5 ± .5 i rt 3
Als ik dan alles terugreken naar a kom ik uit op in beide gevallen uit op 1,53 (zegt mijn GR)
Ik zat nu wel op wolframalpha naar het definitieve antwoord te kijken, maar nee, geen idee hoe ze daaraan komen.
Je hebt nu m3 = -½ + i∙½√3 en n3 = -½ - i∙½√3 (of omgekeerd),
aangezien het product van m3 en n3 gelijk moet zijn aan 1 omdat ook mn = 1, terwijl de som van m3 en n3 gelijk moet zijn aan -1 aangezien m3 + n3 + 1 = 0. Nu maar weer even zelf verder denken ...
Het lijkt erop alsof je hier het interval waarover je r neemt als constant beschouwt, maar dat is niet zo als je p varieert ...quote:
Ik snap trouwens niet waar het bij mij mis gaat. Ik probeerde bolcoördinaten toe te passen en dan bereken je dus
Ik snap je redenatie, maar uiteindelijk staan alle regels waar m en n aan moeten voldoen hier op papier. Blijkbaar wil je op een andere manier dan n = 1/m n en m 'ontrafelen'?
[ Bericht 0% gewijzigd door #ANONIEM op 21-05-2012 01:10:52 ]
[ Bericht 0% gewijzigd door #ANONIEM op 21-05-2012 01:10:52 ]
Je hebt de substitutie x = m + n gemaakt en onder de voorwaarde mn = 1 de waarden van m3 en n3 gevonden. Nu is het dus inderdaad zaak m en n te vinden, maar hoe ...quote:
Ik snap je redenatie, maar uiteindelijk staan alle regels waar m en n aan moeten voldoen hier op papier. Blijkbaar wil je op een andere manier van n = 1/m n en m 'ontrafelen'?
Als ik de vergelijkingen m6 + m3 +1 = 0 en m3 + n3 + 1 = 0 combineer kom ik uit dat m3*2 = n3 = m6
Uitgaande van de regel m3 = -½ + i∙½√3
(-½ + i∙½√3)3 = 1
Waarom heb ik totaal niet het gevoel dat mij dit verder helpt.
Uitgaande van de regel m3 = -½ + i∙½√3
(-½ + i∙½√3)3 = 1
Waarom heb ik totaal niet het gevoel dat mij dit verder helpt.
Dit is werkelijk echt wazig. Leuk probleempje zadel je me mee op, en ik kan bijna niet slapen voordat ik dit heb opgelost. Om half 5 eruit, en daarna een hele dag naar school...
Vooruit, verder.
Als m6 = n3 dan geldt natuurlijk ook m2 = n
Vooruit, verder.
Als m6 = n3 dan geldt natuurlijk ook m2 = n
Ik begrijp dat je het een fascinerend probleem vindt, en je zit ook op de goede weg, maar ik zou als ik jou was nu toch maar gaan slapen, anders is het zo half vijf en heb je geen bed gezien.quote:
Dit is werkelijk echt wazig. Leuk probleempje zadel je me mee op, en ik kan bijna niet slapen voordat ik dit heb opgelost. Om half 5 eruit, en daarna een hele dag naar school...
Ik kom er echt niet uit. m^6 = n^3 en m^2 = n
n√n= 1
n + √n = x
met n = 3√(-0.5 + 0.5i√3)
Waarom klopt dit niet
[ Bericht 1% gewijzigd door #ANONIEM op 21-05-2012 02:01:38 ]
n√n= 1
n + √n = x
met n = 3√(-0.5 + 0.5i√3)
Waarom klopt dit niet
[ Bericht 1% gewijzigd door #ANONIEM op 21-05-2012 02:01:38 ]
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |