Geometrie in graancirkels

Je bijt je vast in iets wat helemaal niet de issue is. Niemand die zal stellen dat de opgaaf eenvoudig is.
Het is niet voor niets een millenia oud 'vraagstuk'.

Het gaat om het veronderstelde verband met de patronen in graancirkels.
Waarbij totaal niet is vast te stellen of die patronen wel volgens de 'spelregels' tot stand zijn gekomen.

& dat het geven van een paar extra benaderingen niet bijster spectaculair is op intergalactisch niveau. Imho.

quote:

Op zaterdag 2 maart 2013 00:50 schreef Probably_on_pcp het volgende:
Kun je specificeren over welke resultaten je het hier hebt?

Het filmpje.

Kan best zijn dat men nieuwe benaderingen heeft voor dit fenomeen maar bestaat de mogelijkheid dat dit al eens eerder toegepast is in design want spelen met vormen is iets voor kunstenaars en designers in streven naar natuurlijke harmonie in oogstrelende vormen. De natuur, Architectuur,overig ontwerp en caleidoscopen waren er al eerder dan de graancirkels en deze lieten ons al kennismaken met mooie combinatievormen. Misschien zien we de schoonheid van effectiviteit van simpele vormen wel niet zo meer en zijn de graanvelden wellicht het nieuwe podium voor kunstenaars om dit te etaleren, zoals het witte doek dat is bij film. Omdat het anders gewoon nergens bewonderd wordt. Als je tekeningen in een museum hangt dan haalt men z'n schouders op.. gooi je 't in een graanveld dan zit zelfs SBS erbovenop oid en bereik je de massa.

Misschien heb ik 't helemaal fout maar in de hagia sofia komt 'squaring the circle' ook voor en is 't ook nog naar "3D" uitgewerkt.De koepel in het midden staat volledig los trouwens', er worden geen ondersteunende pilaren gebruikt.





Het oude Teleac logo?



En zo zijn er volgens mij bakken vol te vinden op brandsoftheworld.com. Het is toch niet dat dit pas sinds de komst van Graancirkels onder de aandacht komt, de presentatie is alleen iets beter.

[ Bericht 3% gewijzigd door Beathoven op 02-03-2013 10:50:24 ]

quote:

Op zaterdag 2 maart 2013 02:29 schreef Probably_on_pcp het volgende:
Blijkbaar heb je het filmpje idd niet goed bekeken. Ik heb toevallig net beide voorbeelden in een bestandje gezet:

Dat had ik al kenbaar gemaakt he.
Ben er al snel doorheen gaan skippen, vanwege het niet boeiende gehalte. Iets wat los staat van de 'inhoud', overigens. Je vroeg om een inhoudelijke discussie over het onderwerp uit het filmpje. Ik probeer in die behoefte te voorzien, maar moet bekennen dat graancirkels me eigenlijk al 20 jaar niet meer interesseren.

Iets wat ik me ook afvraag, wat mogelijk wel is genoemd in het filmpje (maar echt geen zin om het nog eens, aandachtig, te bekijken) is het volgende: In hoeverre heeft de onderzoeker de graancirkels waarvan vaststaat dat ze zogezegd "nep" zijn (= door mensen gemaakt) uitgesloten ?

Voor een enigsinds correcte analyse moet je jezelf wel beperken tot die paar procent waarvan men vermoed dat ze "echt" zijn (= door veronderstelde buitenaardse entiteiten gemaakt)

Vooral ook omdat het ontstaan van dit soort patronen inherent is aan het graancirkelontwerp.
Het wordt zelfs op vergelijkbare manier opgezet. (paaltje + touw van bepaalde lengte == "passer" + "lat")

quote:

[ afbeelding ]

[ afbeelding ]

Het kan aan mij liggen, maar ik zie niet hoe men in beide plaatjes tot de eerste stappen met cirkels komt, gegeven de 'opdracht' (dus zonder te rekenen)

Hoe verdeel je b.v. de grote cirkel direct in 3 kleine, gelijke, cirkels (zonder de breedte te meten en delen door 3 ?)

Bij plaatje 2, hoe komt men zo "spontaan" bij de afmeting van de 4 cirkels ?

Het komt op mij over als een staaltje "terug redeneren", of moet ik de plaatjes wat stappen betreft achterstevoren interpreteren ? Dan nog klopt het niet helemaal volgens mij.

quote:

Nee maar wel op aards niveau en daarom verdient het onze aandacht.

Een beetje, wellicht, maar nogmaals, ik zie geen enkel belang in extra benaderingswijzen voor een onoplosbare uitdaging. Dit is uiteraard slechts een mening.

quote:

Dus de resultaten uit het filmpje vond je niet bijster interessant, maar hierboven zeg je dat er niet te controleren is of de resultaten volgens de spelregels tot stand zijn gekomen....

Das geen kwestie van "maar", het eerste is mede een gevolg van het tweede

quote:

Inderdaad blijkt weer dat je niet helemaal overziet waar het hier nou precies omgaat. De voorbeelden uit het filmpje laten juist duidelijk zien dat het wel volgens de spelregels tot stand is gekomen. Daarnaast heb ik op het internet nog niet veel voorbeelden kunnen vinden van de "oude" methode. Alleen dus die ene die ik vlak hiervoor heb gepost, met al die berekeningen erbij.

En die oplossing is redelijk simpel maar als je kijkt naar de oplossingen hierboven die gevonden zijn in de graancirkels, die zijn nog veel simpeler omdat je alleen maar gebruik hoeft te maken van cirkels en rechte lijnen die in een duidelijk verband staan tot elkaar.

Zie hierboven.

quote:

Op zaterdag 2 maart 2013 00:40 schreef Probably_on_pcp het volgende:

[..]

[..]

[..]

Ik zeg t niet helemaal goed. Je mag wel rekenen, maar het is geen kwestie van een vergelijking neerzetten "oppervlakte cirkel = oppervlakte vierkant" en dan oplossen. Je moet het maken met een liniaal en een passer. Kun je wel zeggen dat het makkelijk is, maar probeer het zelf eens zou ik zeggen.

Ik krijg de indruk dat jullie alle drie niet echt snappen wat er moet gebeuren. Hier een voorbeeld:

Constructie kwadratuur met passer en lineaal (Benadering kwadratuur met 4 ∕ √ φ )

[ afbeelding ]
-Neem een willekeurig middelpunt.
-Teken de blauwe cirkel met een straal van 1 ∕ √ φ (= 0,786). (is natuurlijk ook te construeren).
-Teken de zwarte cirkel met een straal van 1.
-Teken de twee diagonalen (hoek = 45 graden)
-Neem een centerpunt op het snijpunt van de blauwe cirkel en de x-as.
-Neem de rode koorde in de passer, zoals aangegeven, en trek de rode cirkelboog totdat deze de zwarte cirkel snijdt.
-Op het snijpunt van de rode – en de zwarte cirkelboog wordt er een verticale snijlijn (paars) getrokken.
-Neem nu een centerpunt op het snijpunt van de diagonaal, in het eerste kwadrant, met de zwarte cirkel.
-Neem hieruit de straal tot in het snijpunt van de van de paarse verticale lijn en de x-as.
-Trek de groene cirkelboog.
-Het snijpunt van de groene cirkelboog met de zwarte cirkel geeft nu de locatie van de bovenste horizontale zijde van de vierhoek.

Herhaal dit voor de overige zijden. (zie onder).

[ afbeelding ]

[ afbeelding ]

Dan het bewijs dat het bovenstaande klopt:

Algebraïsch bewijs van de kwadratuur.

[ afbeelding ]

[ afbeelding ]

[ afbeelding ]

[ afbeelding ]

[ afbeelding ]

[ afbeelding ]

In mijn berekeningen voor de benadering van de oppervlakte van een cirkel maakte ik gebruik van de door mij gevonden verhouding:

[ afbeelding ]

http://marcroosblog.blogs(...)-kwadratuur-van.html

Dus als het allemaal zo simpel is volgens jullie drie, kom zelf dan eens met een oplossing om met passer en liniaal een quadratuur te maken (squaring the circle).

Ik ben benieuwd

Zo moeilijk is het toch niet?

cirkel met straal van 10 meter, oppervlakte is 100*pi, laten we zeggen 314
vierkant zijde is wortel 314, 17.72
om het vierkant in het midden van de cirkel te krijgen, begin je met een hoe die wortel (8.86^2+8.86^2) vanaf het middelpunt ligt, is 12.53 meter.

Dus je hebt nodig:
2* een touw van 10 meter
een touw van 17.72
een touw van 12.53*2

Je kiest een punt. Loopt een rondje met het touw van tien meter.
Dan vanuit het punt loop je tegenovergesteld 12.53 meter
Vanuit die twee punten loop je met 17.72 meter tot je elkaar tegenkomt.
Dit doe je allebei de kanten op

voila, cirkel en vierkant met zelfde middelpunt en zelfde oppervlakte.

quote:

Op zaterdag 2 maart 2013 23:35 schreef Probably_on_pcp het volgende:

[..]

Sorry maar je begrijpt het niet. Het gaat erom dat er in de graancirkels een stappenplan verborgen ligt, hoe je dus met passer en liniaal kunt komen tot nieuwe benaderingen van squaring the circle (quadratuur).

Het gaat er niet om dat de quadratuur uiteindelijk wordt weergegeven met een vierkant en een cirkel, het gaat om de nieuwe benadering die geboden wordt om de quadratuur te bereiken.

Nee, mijn reactie was dat het niet moeilijk was een vierkant en cirkel met dezelfde oppervakte in een graanveld te maken.

Jij reageerde met als limitet "zonder te rekenen"

Ik reageerde met: hoezo kun je niet rekenen

jij reageerde met: als het dan zo gemakkelijk is een vierkant en cirkel in een graanveld te maken met dezelfde oppervlakte, laat dan maar zien hoe.

Dat heb ik net laten zien.

quote:

Op zaterdag 2 maart 2013 23:35 schreef Probably_on_pcp het volgende:

[..]

Sorry maar je begrijpt het niet. Het gaat erom dat er in de graancirkels een stappenplan verborgen ligt, hoe je dus met passer en liniaal kunt komen tot nieuwe benaderingen van squaring the circle (quadratuur).

Het gaat er niet om dat de quadratuur uiteindelijk wordt weergegeven met een vierkant en een cirkel, het gaat om de nieuwe benadering die geboden wordt om de quadratuur te bereiken.

Je ziet idd. een ontwikkeling in graancirkels, maar komt dat niet omdat de makers steeds bedrevener worden en hun best blijven doen om iets bijzonders neer te zetten?
Het komt me nl. een beetje vreemd voor dat buitenaardse wezens deze methode kiezen om zich kenbaar te maken en daarbij heel goed rekening houden met de psychologie van de mens, zodat er geen paniek zou ontstaan. Je zou denken dat ze ons dan heel goed zouden moeten kennen, ofwel dat de psyche van intelligente wezens overal hetzelfde is.
En hoe doen ze het dan? Reizen ze helemaal hier naartoe om zich ergens verborgen te houden en 's nachts patronen in graanvelden te maken die je alleen vanuit de lucht kunt zien?
En dan? Reizen ze weer terug of houden ze zich ergens verborgen, decennia lang totdat de mensheid er klaar voor is? In het ene geval moeten ze steeds wel heel erg ver reizen, in het andere hebben ze wel heel veel geduld.

quote:

Op zaterdag 2 maart 2013 13:07 schreef R0N1N het volgende:

Hoe verdeel je b.v. de grote cirkel direct in 3 kleine, gelijke, cirkels (zonder de breedte te meten en delen door 3 ?)

Je kunt elke rechthoek zoals hieronder in drie delen verdelen. En dat is weer makkelijk op een cirkel toe te passen; bijvoorbeeld zoals ik hieronder getekend heb.

quote:

Op zondag 3 maart 2013 14:54 schreef GrumpyFish het volgende:
Je kunt elke rechthoek zoals hieronder in drie delen verdelen. En dat is weer makkelijk op een cirkel toe te passen; bijvoorbeeld zoals ik hieronder getekend heb.

[ afbeelding ]

De nadruk in deze ligt dan ook op het woordje "direkt". Niet dat het onmogelijk is.
Je kunt om te beginnen niet zomaar een rechthoek tekenen om je cirkel heen.

Met het bepalen van de hoeken alleen ben je al 9 a 10 "stappen" verder.

Om bij "stap 3" te komen van het plaatje, ben je dus eigenlijk al op "stap 30".
Voor "stap 4" moet je dezelfde "30" stappen weer doorlopen. (heb ze niet exact geteld, hangt er ook vanaf wat je een "stap" noemt. (het trekken van iedere lijn of cirkel leek mij het handigst))
(grappig genoeg lijkt het resultaat op een muis )

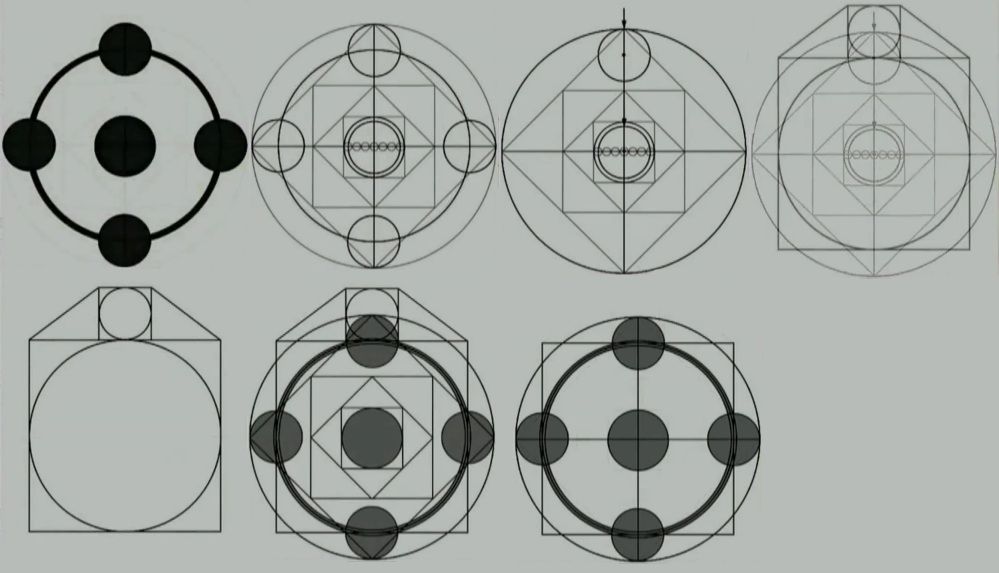
... en dan de eerste afbeelding van de tweede rij ... Die vier kleine cirkels aan de buitenkant, komen daar ook niet zomaar. Nu lijkt het of ze zo zijn neergeplempt. Hoe kom je op het middelpunt ?
... weer zoveel stappen verder...

Hoezo, een "eenvoudige benadering" ?

quote:

Op zondag 3 maart 2013 23:59 schreef Probably_on_pcp het volgende:
Ah tuurlijk

Moet echt even weer wat dingen opfrissen van Wiskunde B van a long long time ago

Dat is ook juist de leuke kant van TRU, dingen uitzoeken, uitproberen en opfrissen na 20 jaar,

Deze hele opgaaf draait daar ook om he. Het is de "reis" die van belang is, niet het (onhaalbare) doel, in deze.

quote:

Op zaterdag 2 maart 2013 02:29 schreef Probably_on_pcp het volgende:

[..]

Blijkbaar heb je het filmpje idd niet goed bekeken. Ik heb toevallig net beide voorbeelden in een bestandje gezet:

[ afbeelding ]

Misschien kijk ik er overheen, maar ik zie het even niet. In welk plaatje wordt een cirkel gesquared?

quote:

Op dinsdag 5 maart 2013 08:18 schreef GrumpyFish het volgende:
Misschien kijk ik er overheen, maar ik zie het even niet. In welk plaatje wordt een cirkel gesquared?

Geen van 2.
Is een kwestie van terugredeneren.

Bij het eerste plaatje is de laatste "stap" het startpunt voor de "onderzoeker". Als je een cirkel tekent die alle 4 de "satelieten" raakt, vormen de middelpunten van die 4 cirkels de hoeken van het vierkant.

Alle andere afbeeldingen/stappen daarvoor is speculatie (& een gigantische berg tekenwerk, die slechts ten dele wordt getoond)

quote:

Op dinsdag 5 maart 2013 11:15 schreef R0N1N het volgende:

[..]

Geen van 2.
Is een kwestie van terugredeneren.

Bij het eerste plaatje is de laatste "stap" het startpunt voor de "onderzoeker". Als je een cirkel tekent die alle 4 de "satelieten" raakt, vormen de middelpunten van die 4 cirkels de hoeken van het vierkant.

Alle andere afbeeldingen/stappen daarvoor is speculatie (& een gigantische berg tekenwerk, die slechts ten dele wordt getoond)

Laat ik het anders formuleren:

Bij het eerste plaatje -met de 16 tekeningen/stappen- is m.i. nergens een cirkel te zien met een vierkant met (bij benadering) dezelfde oppervlakte. Maar misschien zie ik het verkeerd.

Wat jij volgens mij beschrijft, en wat het plaatje laat zien is:
satellieten met r_sat. die aan de binnnenzijde geraakt worden door een cirkel met r_cirkel = 9r_sat.. Een vierkant waarvan de hoekpunten in het middelpunt van de satelliet ligt. Correct?

Maar die cirkel en dat vierkant hebben bij lange na niet dezelfde oppervlakte... Misschien kan iemand in dat plaatje aangeven om welke cirkel en vierkant het gaat?

In het tweede plaatje -met 7 tekeningen/stappen- kan ik nog wel een cirkel en vierkant vinden met ongeveer dezelfde oppervlakte (al scheelt dat nog ruim 3%), maar vind ik het nog onduidelijk hoe het geheel is opgebouwd (en of ik het dus juist heb getekend).

quote:

Op dinsdag 5 maart 2013 18:20 schreef GrumpyFish het volgende:

[..]

Laat ik het anders formuleren:

Bij het eerste plaatje -met de 16 tekeningen/stappen- is m.i. nergens een cirkel te zien met een vierkant met (bij benadering) dezelfde oppervlakte. Maar misschien zie ik het verkeerd.

Wat jij volgens mij beschrijft, en wat het plaatje laat zien is:
satellieten met r_sat. die aan de binnnenzijde geraakt worden door een cirkel met r_cirkel = 9r_sat.. Een vierkant waarvan de hoekpunten in het middelpunt van de satelliet ligt. Correct?

Maar die cirkel en dat vierkant hebben bij lange na niet dezelfde oppervlakte... Misschien kan iemand in dat plaatje aangeven om welke cirkel en vierkant het gaat?

In het tweede plaatje -met 7 tekeningen/stappen- kan ik nog wel een cirkel en vierkant vinden met ongeveer dezelfde oppervlakte (al scheelt dat nog ruim 3%), maar vind ik het nog onduidelijk hoe het geheel is opgebouwd (en of ik het dus juist heb getekend).

Ik snap wat je bedoelt.
De laatste twee tekeningen/stappen, die met de afwijkende achtergrond kleuren, zouden de graancirkel (laatste) & cirkel + vierkant (één na laatste) zijn. DAT zijn dus de cirkel en het vierkant wat jij zoekt.

... maar dat is wel een hele grove benadering inderdaad ...

quote:

Op dinsdag 5 maart 2013 20:19 schreef R0N1N het volgende:

[..]

Ik snap wat je bedoelt.
De laatste twee tekeningen/stappen, die met de afwijkende achtergrond kleuren, zouden de graancirkel (laatste) & cirkel + vierkant (één na laatste) zijn. DAT zijn dus de cirkel en het vierkant wat jij zoekt.

... maar dat is wel een hele grove benadering inderdaad ...

Als in dat eerste plaatje de op een na laatste tekening/stap de gesquarde circle moet voorstellen, is de foutmarge wel erg groot. Het oppervlakte van de cirkel is 27% groter dan die van het vierkant.

Als dat van buitenaardse intelligentie moet getuigen, is het een godswonder dat ze hier uberhaupt geraakt zijn

quote:

Op dinsdag 5 maart 2013 20:53 schreef GrumpyFish het volgende:
Als in dat eerste plaatje de op een na laatste tekening/stap de gesquarde circle moet voorstellen, is de foutmarge wel erg groot. Het oppervlakte van de cirkel is 27% groter dan die van het vierkant.

Als dat van buitenaardse intelligentie moet getuigen, is het een godswonder dat ze hier uberhaupt geraakt zijn

Indeed.

... en ongetwijfeld heeft dit inmiddels al de nodige mensen geinspireerd dit als basis te nemen voor een ontwerpje of 2, maar dan wel gewoon op de PC uitgewerkt, met een teken programma b.v. (dat zou ik doen iig, aangezien dat ook m'n werk is )

_{Weet er nog iemand een weilandje ?}

quote:

Op dinsdag 5 maart 2013 21:49 schreef R0N1N het volgende:

[..]


Indeed.

... en ongetwijfeld heeft dit inmiddels al de nodige mensen geinspireerd dit als basis te nemen voor een ontwerpje of 2, maar dan wel gewoon op de PC uitgewerkt, met een teken programma b.v. (dat zou ik doen iig, aangezien dat ook m'n werk is )

_{Weet er nog iemand een weilandje ?}

Ik heb die twee tekeningen ook even in cad gezet om te kijken of het een beetje te doen was, en om de oppervlaktes eruit te krijgen