SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Al eerder gepost, alleen blijkbaar op de verkeerde plek!
Ik heb momenteel een probleem. In mijn methode, getal en ruimte, wordt blijkbaar niet uitgelegd hoe je integralen en riemannsommen (de Sigma-notatie) uitrekent, slechts op je GR.
Hierbij de vraag: hoe moet ik uit het hoofd en
uitrekenen?
Ik heb momenteel een probleem. In mijn methode, getal en ruimte, wordt blijkbaar niet uitgelegd hoe je integralen en riemannsommen (de Sigma-notatie) uitrekent, slechts op je GR.
Hierbij de vraag: hoe moet ik uit het hoofd en
enuitrekenen?
uitrekenen?
Riemannsommen worden in de praktijk alleen met de computer gebruikt om integralen uit te rekenen die "lastig" zijn. Als je een goede benadering wil met een Riemannsom dan moet je een hele kleinequote:Op zondag 13 november 2011 13:38 schreef Lukep het volgende:
Al eerder gepost, alleen blijkbaar op de verkeerde plek!
Ik heb momenteel een probleem. In mijn methode, getal en ruimte, wordt blijkbaar niet uitgelegd hoe je integralen en riemannsommen (de Sigma-notatie) uitrekent, slechts op je GR.
Hierbij de vraag: hoe moet ik uit het hoofd [ afbeelding ] en
[ afbeelding ] uitrekenen?
Het kan natuurlijk wel met de hand. Neem bijvoorbeeld de eenvoudige functie f(x)=x (dan krijgen we ook niet zo'n moeilijke som). Stel dat we die willen integreren (met een Riemann som) van 0 tot 2. Neem nu een Delta x van bijvoorbeeld 0.1 (hoe kleiner je die neemt, hoe beter je benadering). Nu moeten we dus 20 termen gaan sommeren:
Nu is xk de x-waarde in het k-de interval. Maar in zo'n interval is f niet constant, dus laten we het punt nemen aan de linkerkant van ieder interval. Dan moeten we berekenen
Ik gebruik hier dus dat xk = 0.1k en de standaardformule voor een rekenkundige reeks.
We hebben dus berekend dat de oppervlakte onder de grafiek f(x)=x met x tussen 0 en 2 ongeveer 1.9 is. Omdat je in feite de oppervlakte van een eenvoudige driehoek berekent in dit geval, hadden we direct kunnen inzien dat de oppervlakte (exact) 2 is. (basis*hoogte /2 = 2*2/2=2).
Ik nam nu voor xn steeds het meest linker punt in een intervalletje. Dat is de waarde waar f zijn kleinste waarde aanneemt. Op deze manier hebben we dus met Riemannsommatie bepaald dat de oppervlakte minstens 1.9 is (dat klopt dus ook). Verder kan je ook op ieder interval het maximum bepalen van de functie en daarover sommeren, zodat je ook een bovengrens voor de integraal hebt. Als je je
Dit hele proces doe je eigenlijk alleen maar als je een lastige integraal hebt. Daarmee bedoelde ik een integraal die geen primitieve heeft. Een primitieve is het omgekeerde van een afgeleide. In andere woorden: als F de primitieve is van f, dan geldt F'=f. Als een functie wel een primietieve heeft dan kan je een integraal als volgt berekenen:
waarbij F dus weer de primitieve is van f.
Voorbeeld:
Ik gebruik hier dat
Helaas kan dit niet altijd. De functie f(x)=e^x² heeft bijvoorbeeld geen primitieve (d.w.z. je kan het niet uitdrukken in standaard functies als sin, log, exp, etc). Om toch een waarde te vinden voor je integraal kan je dan Riemannsommatie gebruiken.
Als je de bewijzen wil zien, zie: http://en.wikipedia.org/wiki/Fundamental_theorem_of_calculus .
[ Bericht 0% gewijzigd door thenxero op 13-11-2011 14:21:53 ]
Bravo, geweldig uitgelegd! Te zeggen dat je uitleg goed was, zou een understatement zijn 
.
Ik heb echter een klein probleem (waarschijnlijk een zeer simpele en 'domme' vraag, alleen ik zie hem op het moment niet).
Waarom is xk = 0.1k? Waarom verdwijnt de functie f(xk) en komt er slechts xk voor in de plaats als je voor Δx 0.1 neemt?
Als laatste stel vragen: waar komt de 20 vandaan (en waarom), en waarom vermenigvuldig je die met 19/2 (hoe komt 19/2 er überhaupt te staan)?
.Ik heb echter een klein probleem (waarschijnlijk een zeer simpele en 'domme' vraag, alleen ik zie hem op het moment niet).
Waarom is xk = 0.1k? Waarom verdwijnt de functie f(xk) en komt er slechts xk voor in de plaats als je voor Δx 0.1 neemt?
Als laatste stel vragen: waar komt de 20 vandaan (en waarom), en waarom vermenigvuldig je die met 19/2 (hoe komt 19/2 er überhaupt te staan)?
Probeer eens een tekening te maken bij het (eenvoudige) voorbeeld dat thenxzero uitwerkt. Het idee is dat je de 'oppervlakte onder de curve' (in dit geval een rechte lijn) over een bepaald interval (hier [0,2]) kunt benaderen door die oppervlakte in smalle verticale 'reepjes' te verdelen, en dan elk reepje bij benadering te beschouwen als een rechthoek, waarvan de oppervlakte uiteraard eenvoudig is te bepalen. De benadering wordt dan steeds beter naarmate de rechthoeken (reepjes) smaller worden. We nemen verticale reepjes, omdat de 'hoogte' van elk reepje (rechthoek) dan bij benadering de functiewaarde ter plaatse is, terwijl we de breedte van alle reepjes hetzelfde kunnen nemen (dat hoeft niet, maar is wel zo gemakkelijk). Als je nu het interval [0, 2] in bijvoorbeeld 20 gelijke stukjes (deelintervallen) verdeelt, dan heeft elk verticaal reepje dus een breedte van 0,1. Die twintig deelintervallen kun je voorstellen als [xk, xk+1] met xk = 0,1∙k. en k = 0..19.quote:
Bravo, geweldig uitgelegd! Te zeggen dat je uitleg goed was, zou een understatement zijn
Ik heb echter een klein probleem (waarschijnlijk een zeer simpele en 'domme' vraag, alleen ik zie hem op het moment niet).
Waarom is xk = 0.1k? Waarom verdwijnt de functie f(xk) en komt er slechts xk voor in de plaats als je voor Δx 0.1 neemt?
Als laatste stel vragen: waar komt de 20 vandaan (en waarom), en waarom vermenigvuldig je die met 19/2 (hoe komt 19/2 er überhaupt te staan)?
Jazeker, zo ver was ik ook, toch bedankt voor het ophelderen van xk = 0,1∙k!
Alleen het is mij nog steeds niet duidelijk waarom de functie f(xk) plaats maakt voor de standaardformule xk = 0,1∙k. Immers: xk = 0,1∙k is alleen goed voor de x-coordinaten van de deelintervallen, niet de y-waarde/hoogte zoals f(xk).
Daarnaast is het mijn nog steeds onduidelijk waarom plotseling het sigma-teken met een 20 en 19/2 verwisselt wordt. Het is mij natuurlijk duidelijk dat 20 de hoeveelheid deelintervallen is enz enz, maar waarom de 20 dan te vermenigvuldigen met 19/2?
Alleen het is mij nog steeds niet duidelijk waarom de functie f(xk) plaats maakt voor de standaardformule xk = 0,1∙k. Immers: xk = 0,1∙k is alleen goed voor de x-coordinaten van de deelintervallen, niet de y-waarde/hoogte zoals f(xk).
Daarnaast is het mijn nog steeds onduidelijk waarom plotseling het sigma-teken met een 20 en 19/2 verwisselt wordt. Het is mij natuurlijk duidelijk dat 20 de hoeveelheid deelintervallen is enz enz, maar waarom de 20 dan te vermenigvuldigen met 19/2?
We zijn bezig met de functie f(x)=x. In het bijzonder geldt dus f(xk)=xk.quote:
Jazeker, zo ver was ik ook, toch bedankt voor het ophelderen van xk = 0,1∙k!
Alleen het is mij nog steeds niet duidelijk waarom de functie f(xk) plaats maakt voor de standaardformule xk = 0,1∙k. Immers: xk = 0,1∙k is alleen goed voor de x-coordinaten van de deelintervallen, niet de y-waarde/hoogte zoals f(xk).
Daarnaast is het mijn nog steeds onduidelijk waarom plotseling het sigma-teken met een 20 en 19/2 verwisselt wordt. Het is mij natuurlijk duidelijk dat 20 de hoeveelheid deelintervallen is enz enz, maar waarom de 20 dan te vermenigvuldigen met 19/2?
Wat betreft de sommatie, voor een rekenkundige rij geldt in het algemeen dat de som gelijk is aan het aantal termen gedeeld door twee, maal (de eerste term + de laatste term). In dit geval dus 20/2 * (0+19). Zie ook de wiki.
Bedankt voor het compliment
Dringend vraagje mensen...
Ik wil graag het volgende berekenen.
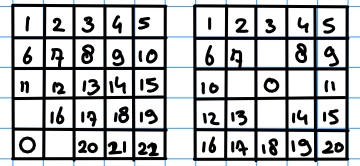
Ik heb een bord van 5x5. Nu kan ik 1 steen op 25 verschillende plekken leggen. Nu wil ik graag weten hoeveel combinaties er zijn wanneer 2 stenen op het veld leg (antwoord weet ik al). De enigste twee regels die er zijn is dat de 2 stenen niet direct langs elkander mogen liggen. Hieronder zie je 2 voorbeelden. In de linker zijn er nog 22 mogelijkheden en in de rechter 20.
Nu wil ik dus weten op hoeveel combinaties er zijn als er 1 steen (25), 2 stenen (22*4 + 21*12 + 20*9 = 520), 3 stenen (???) op het veld liggen.
Is er een elegante methode om dit te berekenen?
Ik wil graag het volgende berekenen.
Ik heb een bord van 5x5. Nu kan ik 1 steen op 25 verschillende plekken leggen. Nu wil ik graag weten hoeveel combinaties er zijn wanneer 2 stenen op het veld leg (antwoord weet ik al). De enigste twee regels die er zijn is dat de 2 stenen niet direct langs elkander mogen liggen. Hieronder zie je 2 voorbeelden. In de linker zijn er nog 22 mogelijkheden en in de rechter 20.
Nu wil ik dus weten op hoeveel combinaties er zijn als er 1 steen (25), 2 stenen (22*4 + 21*12 + 20*9 = 520), 3 stenen (???) op het veld liggen.
Is er een elegante methode om dit te berekenen?
En wat is regel 2?quote:Op zondag 13 november 2011 20:36 schreef Dale. het volgende:
Dringend vraagje mensen...
Ik wil graag het volgende berekenen.
Ik heb een bord van 5x5. Nu kan ik 1 steen op 25 verschillende plekken leggen. Nu wil ik graag weten hoeveel combinaties er zijn wanneer 2 stenen op het veld leg (antwoord weet ik al). De enigste twee regels die er zijn is dat de 2 stenen niet direct langs elkander mogen liggen. Hieronder zie je 2 voorbeelden. In de linker zijn er nog 22 mogelijkheden en in de rechter 20.
[ afbeelding ]
Nu wil ik dus weten op hoeveel combinaties er zijn als er 1 steen (25), 2 stenen (22*4 + 21*12 + 20*9 = 520), 3 stenen (???) op het veld liggen.
Is er een elegante methode om dit te berekenen?
Gewoon die-hard alle mogelijkheden doorgenomen?quote:
[..]
Euh sorry 1 regelgeen idee waarom ik 2 regels schreef. Maar iig, het aantal combo's is 8844
Waarom wilde je dit berekenen trouwens?
V is een niet-lege , naar boven begrensde deelverzameling van 
. Ik wil een rij in V construeren zodat 1)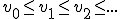
en 2) sup V is de limiet van de rij.
Ik dacht zelf aan: construeer een rij zodat:
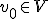
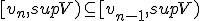
Ik heb nu moeite met het uitleggen dat sup V de limiet van de rij is. Ik dacht aan: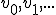
vormen het interval 
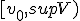waarvan ik wel kan bewijzen dat sup V het supremum is. Ook weet ik niet of het vanzelfsprekend is dat 
.
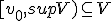Weet iemand hoe ik dit goed op kan schrijven? Of kan ik dit wel zo zeggen?
Ik dacht zelf aan: construeer een rij zodat:
Ik heb nu moeite met het uitleggen dat sup V de limiet van de rij is. Ik dacht aan:
Weet iemand hoe ik dit goed op kan schrijven? Of kan ik dit wel zo zeggen?
De rij met vn=v0 voldoet aan jouw constructie maar v0 hoeft niet gelijk te zijn aan supV. Je kunt het bewijzen door onderscheid te maken tussen of supV in V zit.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dat begrijp ik, omdat het gewoon niet klopt. Zie het tegenvoorbeeld van GlowMouse.quote:
V is een niet-lege , naar boven begrensde deelverzameling van
Ik dacht zelf aan: construeer een rij zodat:
Ik heb nu moeite met het uitleggen dat sup V de limiet van de rij is.
Het is heel goed mogelijk dat sup(V) de limiet is van je rij terwijl sup(V) zelf niet in V zit.quote:Ik dacht aan:
Weet iemand hoe ik dit goed op kan schrijven? Of kan ik dit wel zo zeggen?
Op
1) sup V in Vquote:
Laat v0 = sup V. Construeer de rij v0 = v1 = v2 = ...
Deze rij heeft limiet sup V.
2) sup V niet in V. Laat v0 in V (Kan, V is niet leeg).
Sup V is een bovengrens van V. Voor elke vi in V geldt dus: (vi + supV)/2 < sup V, dus er is een v(i+1) in V met v(i + 1) > (vi + supV)/2. Construeer deze rij.
Sup V is de limiet van deze rij, want stel x is een kleinere bovengrens, dan:
(x+sup V)/2 < sup V dus er is een y in V met y > (x+supV)/2 > x. Tegenspraak.
Heb je er ook rekening mee gehouden dat je deelverzameling V van R geen interval hoeft te bevatten?quote:
Je neemt dus v(i+1) = (v( i ) + sup V)/2, maar hoe weet je of die in je V zit? Misschien zitten er wel allemaal gaten in je verzameling.
Inderdaad niet volledig geformuleerd. Neem voor v(i+1) het kleinste element zo dat v(i + 1) > (vi + supV)/2. Zo had ik het bedacht.
Waarom bestaat dat element dan?quote:
Inderdaad niet volledig geformuleerd. Neem voor v(i+1) het kleinste element zo dat v(i + 1) > (vi + supV)/2. Zo had ik het bedacht.
Een open verzameling in R heeft bijvoorbeeld geen kleinste element. Dus als je begint met v0 en
[ Bericht 18% gewijzigd door thenxero op 20-11-2011 00:01:15 ]
jawelquote:
[..]
Een open verzameling in R heeft bijvoorbeeld geen kleinste element. Dus als je begint met v0 endan bestaat v1 al niet meer.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Als je zegt dat v(i+1) > vi en v(i+1) is bevat in V, is dat dan niet al voldoende voor een constructie?
Nee, pak [0,1) en vi = 0.5-1/iquote:
Als je zegt dat v(i+1) > vi en v(i+1) is bevat in V, is dat dan niet al voldoende voor een constructie?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dat kan. Nu moet je alleen nog laten zien dat die verzameling niet leeg is, dus dat er daadwerkelijk zo'n v_{i+1} is en dat de limiet sup V is. (daarvoor moet je dus nog wel een extra eis hebben voor de keuze van v_{i+1}, anders kan de limiet ook kleiner dan de bovengrens zijn zoals Glowmouse al aangaf).quote:
Heb je gelijk in.en anders weet ik het niet meer.
[ Bericht 4% gewijzigd door thenxero op 20-11-2011 00:37:31 ]
Dit gaat niet werken als je verzameling V slechts een eindig aantal elementen bevat (en dat kan).quote:
Heb je gelijk in.
Is supV dan niet automatisch bevat in V? En daar had ik een simpele oplossing voor.quote:
[..]
Dit gaat niet werken als je verzameling V slechts een eindig aantal elementen bevat (en dat kan).
Bedankt voor de kritische blik allen.
Precies dan is er geen probleem. Het lastige geval is als de sup buiten V ligt.quote:
[..]
Is supV dan niet automatisch bevat in V? En daar had ik een simpele oplossing voor.
Bedankt voor de kritische blik allen.
Ja, dat is waar. Maar je zou een constructie voor je rij {vn} moeten kunnen aangeven onafhankelijk van de aard van V en onafhankelijk van de vraag of sup(V) nu wel of geen element van V is, anders blijft het erg onelegant.quote:
[..]
Is supV dan niet automatisch bevat in V? En daar had ik een simpele oplossing voor.
Bedankt voor de kritische blik allen.
Hallo,
Gegeven is:
f(x) =
{ greatest integer function als x >= 0
{ least integer function als x < 0
Teken hiervan de grafiek, en beantwoord de vraag: "Why is f(x) called the integer part of x?"
---------------------------------
De grafiek tekenen is geen probleem, maar bij het beantwoorden van de vraag had ik in eerste instantie:
Mijn definitie 1: "f(x) is called the integer part of x, omdat de uitkomst ltijd een integer is voor elke waarde van x die je invult".
Echter, een andere definitie die ik kan geven (en die ik beter vind) is:
Mijn definitie 2: "stel ik vul x=2.14 in, dan is de uitkomst f(2.14) = 2. En voor x = -3.5 is de uitkomst f(-3.5) = -3. Dus f(x) is het integer gedeelte van x."
Het antwoord van het boek zegt:
Antwoord boek: "f(x) is called the integer part of x, becase |f(x)| is the largest integer that does not exceed x; i.e. |x| = |f(x)| + y, where 0 <= y < 1."
Ik heb moeite om het antwoord van het boek te begrijpen. Verder vind ik mijn definitie 2 beter dan definitie 1, maar is definitie 2 hetzelfde als het antwoord van het boek, maar dan anders geformuleerd?
M.a.w.; kan iemand mij het antwoord van het boek uitleggen, en aangeven of 'mijn definitie 2' hetzelfde qua betekenis is als het antwoord van het boek?
Bij voorbaat dank.
(p38 opg.32) -> Alle lezers: neger dit, dit is voor mijn eigen referentie
Gegeven is:
f(x) =
{ greatest integer function als x >= 0
{ least integer function als x < 0
Teken hiervan de grafiek, en beantwoord de vraag: "Why is f(x) called the integer part of x?"
---------------------------------
De grafiek tekenen is geen probleem, maar bij het beantwoorden van de vraag had ik in eerste instantie:
Mijn definitie 1: "f(x) is called the integer part of x, omdat de uitkomst ltijd een integer is voor elke waarde van x die je invult".
Echter, een andere definitie die ik kan geven (en die ik beter vind) is:
Mijn definitie 2: "stel ik vul x=2.14 in, dan is de uitkomst f(2.14) = 2. En voor x = -3.5 is de uitkomst f(-3.5) = -3. Dus f(x) is het integer gedeelte van x."
Het antwoord van het boek zegt:
Antwoord boek: "f(x) is called the integer part of x, becase |f(x)| is the largest integer that does not exceed x; i.e. |x| = |f(x)| + y, where 0 <= y < 1."
Ik heb moeite om het antwoord van het boek te begrijpen. Verder vind ik mijn definitie 2 beter dan definitie 1, maar is definitie 2 hetzelfde als het antwoord van het boek, maar dan anders geformuleerd?
M.a.w.; kan iemand mij het antwoord van het boek uitleggen, en aangeven of 'mijn definitie 2' hetzelfde qua betekenis is als het antwoord van het boek?
Bij voorbaat dank.
(p38 opg.32) -> Alle lezers: neger dit, dit is voor mijn eigen referentie
Het probleem met jouw definitie 2 is dat het een voorbeeld is. Je kan een voorbeeld geven van een definitie, maar de definitie zelf kan geen voorbeeld zijn. In plaats van die 2.14 en -3.5 moet je dus een algemene x>0 en x<0 nemen.quote:
Wat er met integer part van een getal x bedoeld wordt is het "gehele gedeelte" van dat getal. Dat is dus het grootste gehele getal dat kleiner of gelijk is aan x.
Als x>0, dan geldt dus
Oja, en definitie 1 is niet volledig. Als je de functie zou nemen f(x)=1 heb je ook een functie die altijd een geheel getal geeft voor iedere x. Maar dat is niet wat er bedoeld wordt met de "integer part of x".
[ Bericht 7% gewijzigd door thenxero op 20-11-2011 14:50:42 ]
Beste thenxero,
Bedankt voor je hulp, echter, ik heb nog steeds moeite om het te begrijpen.
Ik snap dat bij x >= 0, dat f(x) <= x moet zijn, want bij x >= 0 geldt de greatest integer function (zoals gegeven in de opgave).
Zo ook begrij ik dat bij x < 0, dat f(x) >= x moet zijn, want bij x < 0 geldt weer de least integer function (wederom gegeven in de opgave).
Met enkele voorbeelden en waarden:
x >= 0 (greatest integer function) ........... dus f(x) <= x...................bv: x = 2.5, dan f(x) = 2.
x < 0 (least integer function)................... dus f(x) >= x...................bv: x = -3.5, dan f(x) = -3.
Dit is ook makkelijk te zien in de grafiek die ik moest schetsen.
Maar stel nu (wederom een voorbeeld):
voor x >= 0 ............. dus f(x) <=x.............. en x = y + f(x) met 0 <= y < 1. Stel ik vul voor y = 0.9 in (voldoet aan 0 <= y < 1) en voor x = 2.5. Dan krijg ik:
x = y + f(x) voor x >=0 waarbij geldt dat f(x) <= x, en met waardes wordt deze:
2.5 = 0.9 + 2, maar dit klopt toch niet meer, want als ik de 0.9 'naar links breng', krijg ik:
1.6 = 2 ????
Ik raak volledig in de war zodra de y bijgehaald wordt. Als ik waardes in vul, kom ik er niet uit. Hier raak ik dan ook in de knoop
Bedankt voor je hulp, echter, ik heb nog steeds moeite om het te begrijpen.
Ik snap dat bij x >= 0, dat f(x) <= x moet zijn, want bij x >= 0 geldt de greatest integer function (zoals gegeven in de opgave).
Zo ook begrij ik dat bij x < 0, dat f(x) >= x moet zijn, want bij x < 0 geldt weer de least integer function (wederom gegeven in de opgave).
Met enkele voorbeelden en waarden:
x >= 0 (greatest integer function) ........... dus f(x) <= x...................bv: x = 2.5, dan f(x) = 2.
x < 0 (least integer function)................... dus f(x) >= x...................bv: x = -3.5, dan f(x) = -3.
Dit is ook makkelijk te zien in de grafiek die ik moest schetsen.
Maar stel nu (wederom een voorbeeld):
voor x >= 0 ............. dus f(x) <=x.............. en x = y + f(x) met 0 <= y < 1. Stel ik vul voor y = 0.9 in (voldoet aan 0 <= y < 1) en voor x = 2.5. Dan krijg ik:
x = y + f(x) voor x >=0 waarbij geldt dat f(x) <= x, en met waardes wordt deze:
2.5 = 0.9 + 2, maar dit klopt toch niet meer, want als ik de 0.9 'naar links breng', krijg ik:
1.6 = 2 ????
Ik raak volledig in de war zodra de y bijgehaald wordt. Als ik waardes in vul, kom ik er niet uit. Hier raak ik dan ook in de knoop
y is geen willekeurig getal tussen 0 en 1, maar y = |x - f(x)|, oftewel: y is het decimale gedeelte. Wat er dus eigenlijk staat is dat je x kan opdelen in een "integer part" (namelijk f(x)) en een decimal part (y).
Voorbeeld:
Als x = 3.15, dan f(x) = 3 en y = 0.15.
Dus:
3.15 = 3 + 0.15
x = f(x) + y
Voorbeeld:
Als x = 3.15, dan f(x) = 3 en y = 0.15.
Dus:
3.15 = 3 + 0.15
x = f(x) + y
...als ik het zo lees is het inderdaad heel, heeeel erg logisch.Als het nou ook zo in het antwoord stond, zou dat een hoop tijd en moeite schelen..... Hartelijk dank voor je hulp, ik begrijp het nu.
hoe heet de 6 , maar dan in horizontaal spiegelbeeld, zoals in http://en.wikipedia.org/wiki/It%C5%8D%27s_lemma
"Vanity, definitely my favorite sin. . . ."
