SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Nee, want dan zou het triviaal zijn. Je kunt hier makkelijk twee inclusies laten zien.quote:Op maandag 19 september 2011 20:32 schreef Anoonumos het volgende:
[ http://img163.imageshack.us/img163/240/la1li.png (copy/paste deze link) ]
Ik kom niet uit 2. Zou het kunnen dat ze L(S^..) bedoelen i.p.v. L(S)^.. ?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik studeer wiskunde en ben ook zeker niet dol op rekensommen. Gelukkig hoef je bij (pure) wiskunde ook niet veel meer dingen te berekenen dan 1+1=2. Het doorgronden van mooie stellingen, daar hou ik wel van.quote:
Heb een vraag voor jullie wiskundigen, vinden jullie het wel leuk?
Ik hou echt van studeren en ben er dol op, alleen ben meer van de type dikke boeken lezen, aantekeningen maken en verslagen schrijven, terwijl ik ook wel wiskunde iwl leren maar daar meer moeite mee heb...
Ik vind het dan wel zonde om mijn master Elektro te verruilen voor iets simpels als Bestuurskunde ofzo... enkel omdat ik van leeswerk houd. Ben altijd al meer praktisch geweest dan wiskundig, maar toch...
Hoe is het met jullie, houden jullie echt van veel sommen maken?
Ik zie niet wat ik moet doen. Bewijzen dat S = L(S) lukt niet. Moet ik iets met <x,s> = 0 doen? Het probleem is dat medestudenten het ook niet snappen.quote:
[..]
Nee, want dan zou het triviaal zijn. Je kunt hier makkelijk twee inclusies laten zien.
Hoe toon je aan dat twee verzamelingen gelijk zijn?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ze hebben dezelfde elementen, want <x,s> is 0 voor alle s in S als x = 0?. Maar het lijkt me niet dat ze zo'n lange definitie geven voor de verzameling x=0.
De doorsnede van alle deelruimtes waar S in zit. Althans, je hebt ook een definitie met L(S) is de verzameling van alle lineaire combinaties, maar ik denk dat ik daar niks aan heb voor deze opdracht.
Dat laatste hou IK weer niet van, ik vind het wel leuk om te weten hoe men differentieert en de abc formule toepast, maar de gehele theorie hoe dat is bedacht? Laat maar zittenquote:
[..]
Ik ben dan zelf geen officieel wiskundige (io), maar nee, van veeeel sommen maken hou ik iig geval niet. Veel interessanter is het om jezelf een nieuwe wiskunde techniek eigen te maken en de theoretische achtergrond door te krijgen, en ja, dat betekent bij tijd en wijle gewoon de pen ter hand te nemen en het gewoon uit te schrijven.
De doorsnede van alle deelruimtes is toch altijd {0}?quote:
De doorsnede van alle deelruimtes waar S in zit.
- edit: laat maar, S moet deelverzameling zijn van die deelruimtes.
[ Bericht 7% gewijzigd door twaalf op 19-09-2011 22:20:24 ]
De deelverzameling S moet erin zitten.quote:
[..]
De doorsnede van alle deelruimtes is toch altijd {0}?
Bedankt voor de hulp tot dusverre, ik ga er morgen verder mee aan de slag.
Ik denk dat je daar wel wat aan hebt.quote:
De doorsnede van alle deelruimtes waar S in zit. Althans, je hebt ook een definitie met L(S) is de verzameling van alle lineaire combinaties, maar ik denk dat ik daar niks aan heb voor deze opdracht.
Stel groep A staat voor 70% positief en 30% negatief tegenover X, groep B staat voor 40% positief en 60% negatief tegenover X.
Populatie bestaat uit 20 mensen, waarvan 15 uit groep A en 5 uit groep B.
(b) Twee negatieve meningen worden waargenomen, wat is de kans dat beide waarnemingen uit groep B komen?
Is het eindantwoord 0.16?
Populatie bestaat uit 20 mensen, waarvan 15 uit groep A en 5 uit groep B.
(b) Twee negatieve meningen worden waargenomen, wat is de kans dat beide waarnemingen uit groep B komen?
Is het eindantwoord 0.16?
Rare vraag, want dan zou 70% uit groep A, oftewel 10,5 personen een negatieve mening hebben, en het is nogal raar als je halve personen hebt.quote:
Stel groep A staat voor 70% positief en 30% negatief tegenover X, groep B staat voor 40% positief en 60% negatief tegenover X.
Populatie bestaat uit 20 mensen, waarvan 15 uit groep A en 5 uit groep B.
(b) Twee negatieve meningen worden waargenomen, wat is de kans dat beide waarnemingen uit groep B komen?
Is het eindantwoord 0.16?
HJ 14-punt-gift.
Lijst met rukmateriaal!
Lijst met rukmateriaal!
Er staat uit groep A en uit groep B...quote:Op maandag 19 september 2011 23:47 schreef freiss het volgende:
[..]
Rare vraag, want dan zou 70% uit groep A, oftewel 10,5 personen een negatieve mening hebben, en het is nogal raar als je halve personen hebt.
Oh zo, ik las hem verkeerd, ik vulde het woord "bestaat" verder in in de bijzinquote:
[..]
Er staat uit groep A en uit groep B...
De groep A en groep B zijn dus groter
HJ 14-punt-gift.
Lijst met rukmateriaal!
Lijst met rukmateriaal!
0.16 lijkt me wel goed, want 0.4 is de kans dat een negatieve uit groep B komt, dus het kwadraat is de kans dat beide uit groep B komen.
Ja inderdaad, bij (b) ging het om één keer (a) eigenlijk, daar kreeg ik 0.4 uit, als je in de teller en noemer de factoren kwadrateert dan krijg je 0.16 uit.quote:
0.16 lijkt me wel goed, want 0.4 is de kans dat een negatieve uit groep B komt, dus het kwadraat is de kans dat beide uit groep B komen.
Jullie pakken twee mensen aselect uit de steekproef met terugleggen. Terwijl als je er eentje pakt en die komt uit groep B, dan is de kans dat je er nog eentje uit B pakt, kleiner is wanneer je niet teruglegt.
En is 2 het totaal aantal negatieve waarnemingen binnen de groep van 20?
En is 2 het totaal aantal negatieve waarnemingen binnen de groep van 20?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Nee, alleen gegeven dat je twee meningen krijgt die negatief zijn. Je hebt overigens wel gelijk met je eerste commentaar, daar zat ik over te dubben..quote:
Jullie pakken twee mensen aselect uit de steekproef met terugleggen. Terwijl als je er eentje pakt en die komt uit groep B, dan is de kans dat je er nog eentje uit B pakt, kleiner is wanneer je niet teruglegt.
En is 2 het totaal aantal negatieve waarnemingen binnen de groep van 20?
edit; krijg al een idee, wel een pittige vraag gekeken naar hoe lang we hier mee bezig zijn :/
Kostte me 3min om die 0.4 te vinden.
En nog eens 3 om op 0.4 * 8/23 uit te komen.
[ Bericht 22% gewijzigd door GlowMouse op 20-09-2011 00:45:48 ]
En nog eens 3 om op 0.4 * 8/23 uit te komen.
[ Bericht 22% gewijzigd door GlowMouse op 20-09-2011 00:45:48 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Heb je het over mijn vraag? Welke 0.6?quote:Op dinsdag 20 september 2011 00:17 schreef GlowMouse het volgende:
Kostte me 3min om die 0.6 te vinden.
En nog eens 3 om op 0.6 * 8/23 uit te komen.
Ik kom niet helemaal uit de begrippen van rij, iteratie, repetent, etc.
Stel je hebt een transformatie f: A-->A met A eindig, dan is deze rij repetent.
Als je nu de kleinste periode moet vinden, moet je dan:
Een a in A zoeken zodat fk(a)=fl(a) met k-l minimaal is (en dit is dan de kleinste periode),
of moet je de minimale k,l zoeken zodat fk=fl?
Stel je hebt een transformatie f: A-->A met A eindig, dan is deze rij repetent.
Als je nu de kleinste periode moet vinden, moet je dan:
Een a in A zoeken zodat fk(a)=fl(a) met k-l minimaal is (en dit is dan de kleinste periode),
of moet je de minimale k,l zoeken zodat fk=fl?
Ik wil een wiskunde b certificaat halen, waar begin ik? Kan je dat zelf leren?
Ik heb zojuist een proefles bij de loi aangevraagd.
Maar dat is misschien niet de beste manier
Ik heb zojuist een proefles bij de loi aangevraagd.
Maar dat is misschien niet de beste manier
Je kan een cursus volgen zoals bij LOI of speciale instituten, of je vraagt een wiskundestudent of hij je (een paar keer per week) bijles wil geven. Dat laatste is waarschijnlijk goedkoper en misschien ook een stuk prettiger, omdat je altijd 1-1 begeleiding hebt.quote:
Ik wil een wiskunde b certificaat halen, waar begin ik? Kan je dat zelf leren?
Ik heb zojuist een proefles bij de loi aangevraagd.
Maar dat is misschien niet de beste manier
Bij een cursus via de LOI moet je een behoorlijke dosis zelfdiscipline hebben. Beter is 1-1 les lijkt me.
kloep kloep
Ook dan moet je wel genoeg discipline hebben natuurlijk. Je zal voor het grootste gedeelte van de tijd zelf moeten oefenen.quote:
Bij een cursus via de LOI moet je een behoorlijke dosis zelfdiscipline hebben. Beter is 1-1 les lijkt me.
Volgens Wolframalpha is dit true:
Maar dat klopt toch niet? M boven M+1 is toch immers altijd 0?
Maar dat klopt toch niet? M boven M+1 is toch immers altijd 0?
Özil | Ki SY| Son HM| Lee SW| Taeguk Warriors|
Het is triviaal dat het waar is, wat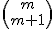 
ook is, immers 
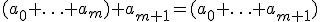is waar voor alle 
.
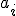heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
De reden waarom ik juist wil weten of het waar is omdat ik via inductie moet bewijzen dat waar is voor elke m ∈ ℕ en gegeven is dat 0 ≤ x ≤ 1. De manier waarop we het tot nu toe hebben moeten doen is ervoor zorgen dat uiteindelijk aan beide kanten de m vervangen zou worden door (m+1), en het leek me zinnig dat aan de linkerkant van de vergelijking te verzorgen door iets aan beide kanten toe te voegen, waarbij ik dus uitkwam opquote:
Het is triviaal dat het waar is, wat
waar is voor elke m ∈ ℕ en gegeven is dat 0 ≤ x ≤ 1. De manier waarop we het tot nu toe hebben moeten doen is ervoor zorgen dat uiteindelijk aan beide kanten de m vervangen zou worden door (m+1), en het leek me zinnig dat aan de linkerkant van de vergelijking te verzorgen door iets aan beide kanten toe te voegen, waarbij ik dus uitkwam op
Özil | Ki SY| Son HM| Lee SW| Taeguk Warriors|
Ja, volgens mij wel. Je zit in ieder geval onnodig moeilijk te doen. De linkerzijde van de ongelijkheid die je moet aantonen is immers gelijk aan:quote:
[..]
De reden waarom ik juist wil weten of het waar is omdat ik via inductie moet bewijzen dat [ afbeelding ] waar is voor elke m ∈ ℕ en gegeven is dat 0 ≤ x ≤ 1.
[snip]
Pak ik het nou helemaal verkeerd aan?
(1) (x + 1)m
Dus wordt gevraagd te bewijzen dat:
(2) (x + 1)m ≤ (m + 1)! voor elke m ∈ ℕ en elke x zodanig dat 0 ≤ x ≤ 1.
Het bewijs van (2) met volledige inductie is eenvoudig. Het is triviaal dat (2) juist is voor m = 1, immers dan reduceert (2) tot:
(3) x + 1 ≤ 2,
en dat is juist aangezien x ≤ 1.
Nu moeten we nog aantonen dat de juistheid van (2) voor een willekeurige m = n ook de juistheid van (2) voor m = n + 1 impliceert. Is (2) juist voor een zekere m = n, dan geldt dus:
(4) (x + 1)n ≤ (n + 1)!
Nu volgt uit 0 ≤ x ≤ 1 dat 1 ≤ x + 1 ≤ 2. Vermenigvuldigen we beide leden van de ongelijkheid (4) met het positieve getal x + 1, dan hebben we dus:
(5) (x + 1)n+1 ≤ (n + 1)!∙(x + 1)
Maar nu volgt uit 0 ≤ x ≤ 1 en n ≥ 1 ook dat x ≤ n en dus
(6) x + 1 ≤ n + 1 < n + 2
En dus hebben we ook:
(7) (n + 1)!∙(x + 1) < (n + 1)!∙(n + 2) = (n + 2)!
Uit (5) en (7) volgt nu:
(8) (x + 1)n+1 < (n + 2)!
En dus a fortiori:
(9) (x + 1)n+1 ≤ ((n + 1) + 1)!
En dit betekent niets anders dan dat (2) juist is voor m = n + 1. De juistheid van (4), i.e. van (2) voor m = n, impliceert dus (9) en daarmee de juistheid van (2) voor m = n + 1,
QED.
Zeer bedanktquote:
[..]
Ja, volgens mij wel. Je zit in ieder geval onnodig moeilijk te doen. De linkerzijde van de ongelijkheid die je moet aantonen is immers gelijk aan:
[uitleg]
QED.
Stom dat ik niet zag dat dat linkerdeel gelijk staat aan (x+1)^m.. Maar ik snap hem nu helemaal, nu maar snel slapen
Özil | Ki SY| Son HM| Lee SW| Taeguk Warriors|
Ja. Hangt ervan af wat je er mee wil doenquote:
Iemand hier ervaring met mathematica 8 van wolfram? Is het handig?
.
is er een makkelijke manier om een parametervoorstelling van het vlak (3, 3, 3) + l(1, -2, -2) +m(-2, -1, -4) om te zetten in een vergelijking? (van de vorm ax+by+cz=d, waarin a b c en d constanten zijn)
Ik weet alleen een manier waarbij je met het uitproduct de normaalvector berekent, maar ik zoek een manier zonder het uitproduct (die is nog niet behandeld, dus ik neem aan dat het de bedoeling is om het zonder uitproduct te doen).
Ik weet alleen een manier waarbij je met het uitproduct de normaalvector berekent, maar ik zoek een manier zonder het uitproduct (die is nog niet behandeld, dus ik neem aan dat het de bedoeling is om het zonder uitproduct te doen).
Finally, someone let me out of my cage
Je kan ook wat punten (l, m) invullen en zo krijg je een stelsel vergelijkingen voor a, b, c, d. Uitproduct lijkt me echter makkelijker.quote:
is er een makkelijke manier om een parametervoorstelling van het vlak (3, 3, 3) + l(1, -2, -2) +m(-2, -1, -4) om te zetten in een vergelijking? (van de vorm ax+by+cz=d, waarin a b c en d constanten zijn)
Ik weet alleen een manier waarbij je met het uitproduct de normaalvector berekent, maar ik zoek een manier zonder het uitproduct (die is nog niet behandeld, dus ik neem aan dat het de bedoeling is om het zonder uitproduct te doen).
Ok, ik was nu zoiets aan het doen ja, het is inderdaad nogal een gedoe. Omdat de normaalvector elke lengte > 0 kan hebben kan je alleen de onderlinge grootte van de componenten afleiden. Maar bedankt, dan ga ik maar zo verderquote:
[..]
Je kan ook wat punten (l, m) invullen en zo krijg je een stelsel vergelijkingen voor a, b, c, d. Uitproduct lijkt me echter makkelijker.
.
Finally, someone let me out of my cage
Ik raad de LOI cursus voor Wiskunde A in ieder geval niet aan.quote:
Bij een cursus via de LOI moet je een behoorlijke dosis zelfdiscipline hebben. Beter is 1-1 les lijkt me.
Het was niet alleen zo dat het antwoordenboekje fouten bevatten (wat al erg hinderlijk is), zelfs sommige vraagstellingen waren compleet fout.
[ Bericht 0% gewijzigd door JohnSpek op 21-09-2011 13:20:42 ]
Behalve Riparius' mooie uitleg, de fout die je in je originele aanpak gemaakt hebt is dat je niet allequote:
[..]
De reden waarom ik juist wil weten of het waar is omdat ik via inductie moet bewijzen dat [ afbeelding ] waar is voor elke m ∈ ℕ en gegeven is dat 0 ≤ x ≤ 1. De manier waarop we het tot nu toe hebben moeten doen is ervoor zorgen dat uiteindelijk aan beide kanten de m vervangen zou worden door (m+1), en het leek me zinnig dat aan de linkerkant van de vergelijking te verzorgen door iets aan beide kanten toe te voegen, waarbij ik dus uitkwam op
niet naar
Het is wel een beetje een vreemde vraag, je kunt ook gewoon gebruiken dat
dit laatste omdat
[ Bericht 5% gewijzigd door keesjeislief op 21-09-2011 13:50:47 ]
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Ik zou zoiets ook niet aan zowel de LOI als NTI toevertrouwen, het regent klachten over die instanties en de kern van het probleem is vaak dat het ze gewoon geen fuck interesseert. Lesstof toveren ze uit alle hoeken en gaten te voorschijn, en als het niet aansluit is dat het probleem van de student. Dat is leuk voor een cursus fotograferen, maar niet voor een serieuze wiskundeopleiding lijkt me.quote:
[..]
Ik raad de LOI cursus voor Wiskunde A in ieder geval niet aan.
Het was niet alleen zo dat het antwoordenboekje fouten bevatten (wat al erg hinderlijk is), zelfs sommige vraagstellingen waren compleet fout.
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Ja ik ben overtuigd, ik ga een leraar zoeken.quote:
[..]
Ik zou zoiets ook niet aan zowel de LOI als NTI toevertrouwen, het regent klachten over die instanties en de kern van het probleem is vaak dat het ze gewoon geen fuck interesseert. Lesstof toveren ze uit alle hoeken en gaten te voorschijn, en als het niet aansluit is dat het probleem van de student. Dat is leuk voor een cursus fotograferen, maar niet voor een serieuze wiskundeopleiding lijkt me.
Als er mensen zijn die goed zijn in natuurkunde en wiskunde (b) en die het goed kunnen uitleggen, pm me even?
Ik heb een diploma op vmbo niveau, en wil graag naar havo niveau toe.
Volgend jaar wil ik starten met een opleiding. (maritiem officier)
Het gaat dus om een periode van een jaar. Ik woon in alphen aan den rijn, en vind 17.50 een mooi uurloon.
Iemand intresse???
Mag je wel gebruik maken van het inproduct van twee vectoren? Als n = (a, b, c) een normaalvector is van je vlak en het eindpunt van de vector p = (3, 3, 3) ligt in je vlak, dan staat voor elke willekeurige (andere) vector v = (x, y, z) met eindpunt in je vlak de verschilvector v - p loodrecht op n zodat het inproduct van deze vectoren gelijk is aan nul:quote:
is er een makkelijke manier om een parametervoorstelling van het vlak (3, 3, 3) + l(1, -2, -2) +m(-2, -1, -4) om te zetten in een vergelijking? (van de vorm ax+by+cz=d, waarin a b c en d constanten zijn)
Ik weet alleen een manier waarbij je met het uitproduct de normaalvector berekent, maar ik zoek een manier zonder het uitproduct (die is nog niet behandeld, dus ik neem aan dat het de bedoeling is om het zonder uitproduct te doen).
(1) n∙(v - p) = 0
En dus hebben we:
(2) a(x - 3) + b(y - 3) + c(z - 3) = 0
Voor de bepaling van a,b en c kun je bedenken dat n = (a, b, c) loodrecht staat op zowel (1, -2, -2) als (-2, -1, -4), zodat het inproduct van n met elk van deze beide weer nul is, dus:
(3) a - 2b - 2c = 0
(4) -2a -b - 4c = 0
Oplossen van dit stelsel waarbij je (bijvoorbeeld) c als een constante beschouwt levert dan a = -(6/5)∙c en b = -(8/5)∙c, zodat de keuze c = 5 dus a = -6 en b = -8 levert. De gevraagde cartesische vergelijking van het vlak is dan:
(5) -6(x - 3) - 8(y - 3) + 5(z - 3) = 0
En dit kun je ook schrijven als:
(6) -6x - 8y + 5z = -27
Dat mag wel denk ik. Ik had al een oplossing gevonden maar jou manier is een stuk mooierquote:
[..]
Mag je wel gebruik maken van het inproduct van twee vectoren? Als n = (a, b, c) een normaalvector is van je vlak en het eindpunt van de vector p = (3, 3, 3) ligt in je vlak, dan staat voor elke willekeurige (andere) vector v = (x, y, z) met eindpunt in je vlak de verschilvector v - p loodrecht op n zodat het inproduct van deze vectoren gelijk is aan nul:
(1) n∙(v - p) = 0
En dus hebben we:
(2) a(x - 3) + b(y - 3) + c(z - 3) = 0
Voor de bepaling van a,b en c kun je bedenken dat n = (a, b, c) loodrecht staat op zowel (1, -2, -2) als (-2, -1, -4), zodat het inproduct van n met elk van deze beide weer nul is, dus:
(3) a - 2b - 2c = 0
(4) -2a -b - 4c = 0
Oplossen van dit stelsel waarbij je (bijvoorbeeld) c als een constante beschouwt levert dan a = -(6/5)∙c en b = -(8/5)∙c, zodat de keuze c = 5 dus a = -6 en b = -8 levert. De gevraagde cartesische vergelijking van het vlak is dan:
(5) -6(x - 3) - 8(y - 3) + 5(z - 3) = 0
En dit kun je ook schrijven als:
(6) -6x - 8y + 5z = -27
, mooi gedaan!
Finally, someone let me out of my cage
simplify: ln (x+1/x-1) * sq. (x+1)(x+2)
ln(x+1) - ln(x-1) * (x+1(x+2)1/2
daar loop ik al vast, die ln is nieuw voor me en ik vind de engels uitleg kut.
ln(x+1) - ln(x-1) * (x+1(x+2)1/2
daar loop ik al vast, die ln is nieuw voor me en ik vind de engels uitleg kut.
Graag wat duidelijker met de haakjes. Staat de wortel binnen de ln? Is het (x+1)/(x-1) of x + 1/x - 1
Wen er maar vast aan, veel vakliteratuur is in het Engels, en dat geldt tegenwoordig voor zowat elk vakgebied.quote:Op donderdag 22 september 2011 17:54 schreef Sokz het volgende:
Daar loop ik al vast, die ln is nieuw voor me en ik vind de engelse uitleg k*t.
ln staat voor logarithmus naturalis oftewel de natuurlijke logaritme, i.e. de logaritme met grondtal e.
Gebruik anders de [tex] tag; in de OP kun je er meer over vinden.quote:
simplify: ln (x+1/x-1) * sq. (x+1)(x+2)
ln(x+1) - ln(x-1) * (x+1(x+2)1/2
daar loop ik al vast, die ln is nieuw voor me en ik vind de engels uitleg kut.
kloep kloep
(ln x+1 ) * WORTEL (x+1)(x+2)
......x-1
Hoop dat het zo duidelijker is.
......x-1
Hoop dat het zo duidelijker is.
Had bij Wiskunde juist niet verwacht dat ik er moeite mee zou hebben (getal is immers een getal) maar voor de rest is 't goed te volgen behalve bij wiskunde.quote:
[..]
Wen er maar vast aan, veel vakliteratuur is in het Engels, en dat geldt tegenwoordig voor zowat elk vakgebied.
ln staat voor logarithmus naturalis oftewel de natuurlijke logaritme, i.e. de logaritme met grondtal e.
Je kunt gebruiken dat ln(a/b) = ln(a) - ln(b) (mits a,b>0), als je niet van breuken houdt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik zit ook te kijken; maar op de opmerking van Glowmouse na zie ik geen mogelijkheid om deze uitdrukking verder te vereenvoudigen.
kloep kloep
Wellicht wordt ln (((x + 1)/(x -1)) ∙√((x + 1)(x + 2))) bedoeld.quote:
Ik zit ook te kijken; maar op de opmerking van Glowmouse na zie ik geen mogelijkheid om deze uitdrukking verder te vereenvoudigen.
Sokz zegt expliciet van niet. Zelfs daarmee zou je niet veel verder komen, je kunt hoogstens de factoren x+1 samennemen. Splitsen van de logaritmes zie ik niet als een versimpeling.quote:
[..]
Wellicht wordt ln (((x + 1)/(x -1)) ∙√((x + 1)(x + 2))) bedoeld.
Jawel, en dan het halfje ervoor halen.quote:
[..]
Splitsen van de logaritmes zie ik niet als een versimpeling.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Is er een eenvoudige manier om te zien dat E(X^4) ongelijk is aan E(X^2)^2 als X standaard normaal verdeeld is?
Ga na wanneer je (in het algemeen) gelijkheid hebt, dan zul je zien dat dat hier niet het geval is.quote:
Dan heb ik alleen maar dat E(X²)² =< E(X^4) toch? Geen strikte ongelijkheid.
je noemt zoiets een gedegenereerde stochast
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Iemand verstand van limieten?
Als limx --> 0+ f(x) = A en limx --> 0- f(x) = B wat is dan de waarde van
(1) limx --> 0+ f(x3 - x)
(2) limx --> 0- f(x2 - x4)
Als limx --> 0+ f(x) = A en limx --> 0- f(x) = B wat is dan de waarde van
(1) limx --> 0+ f(x3 - x)
(2) limx --> 0- f(x2 - x4)
Mandy & Lisa
Tussen 0 en 1 is een hogere macht kleiner dan een lagere macht. Dus x^3-x<0. Als je x van boven naar 0 laat gaan, zal x^3-x van beneden naar 0 gaan. Dus de limiet is B.
Bedenk eens dat x3 - x = x(x2 - 1) en x2 - x4 = x2(1 - x2). Nu jij weer.quote:Op vrijdag 23 september 2011 18:25 schreef xCore het volgende:
Iemand verstand van limieten?
Als limx --> 0+ f(x) = A en limx --> 0- f(x) = B wat is dan de waarde van
(1) limx --> 0+ f(x3 - x)
(2) limx --> 0- f(x2 - x4)
Ik heb hier het volgende:
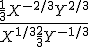
Om de negatieve exponent weg te werken onderin breuk zetten, dus zo:
(
Y^(2/3)
______
(1/3)X^(2/3)
)
/
(
X^(1/3)
________
(2/3)Y^(1/3)
)
Is dit een juiste manier van doen?
En mag je dan de Ytjes en Xjes met elkaar vermenigvuldigen ? Om zo op te lossen...
dan krijg je dus
1x/2y
Om de negatieve exponent weg te werken onderin breuk zetten, dus zo:
(
Y^(2/3)
______
(1/3)X^(2/3)
)
/
(
X^(1/3)
________
(2/3)Y^(1/3)
)
Is dit een juiste manier van doen?
En mag je dan de Ytjes en Xjes met elkaar vermenigvuldigen ? Om zo op te lossen...
dan krijg je dus
1x/2y
Dat was inderdaad de bedoeling .. vraag bestond eigenlijk uit twee componenten, simplify & max domain.quote:
[..]
Jawel, en dan het halfje ervoor halen.
Nee. Je maakt het erg onoverzichtelijk voor jezelf en voor anderen, en dat werkt fouten in de hand, dat blijkt wel. Vermenigvuldig gewoon teller en noemer van je breuk met 3x2/3y1/3, dat levert y/2x.quote:
Ik heb hier het volgende:
Om de negatieve exponent weg te werken onderin breuk zetten, dus zo:
(
Y^(2/3)
______
(1/3)X^(2/3)
)
/
(
X^(1/3)
________
(2/3)Y^(1/3)
)
Is dit een juiste manier van doen?
En mag je dan de Ytjes en Xjes met elkaar vermenigvuldigen ? Om zo op te lossen...
dan krijg je dus
1x/2y
Je hebt gelijk inderdaad, niet erg overzichtelijk.quote:
[..]
Nee. Je maakt het erg onoverzichtelijk voor jezelf en voor anderen, en dat werkt fouten in de hand, dat blijkt wel. Vermenigvuldig gewoon teller en noemer van je breuk met 3x2/3y1/3, dat levert y/2x.
Als ik het met dat vermenigvuldig dan krijg je toch dit right?
Hoe kan ik dit anders schrijven zodat ik de limiet van x naar min oneindig kan bepalen (die - 1/2 is?)
Je kan laten zien dat die bovenste 4 'vervalt' (delen door oneindig)
Dan loop ik vast. Wolfram Alpha deelt door x en gebruikt dan regels die ik nog niet ken. (power law, L'Hospital rule)
Inderdaad delen door x, dit geeft:
(*)
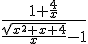en hierin is voor x<0:
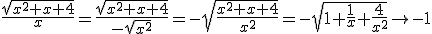als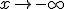 
,
dus (*) convergeert naar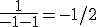
als .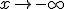
en hierin is voor x<0:
dus (*) convergeert naar
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Hoe bereken ik dat
?
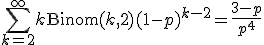Binom staat voor het binomiaalcoëfficiënt.
Het is geen meetkundige rij... maar het staat als rekenopgave in mijn textboek, dus zou toch met pen en papier moeten kunnen.
Binom staat voor het binomiaalcoëfficiënt.
Het is geen meetkundige rij... maar het staat als rekenopgave in mijn textboek, dus zou toch met pen en papier moeten kunnen.
wat een naar ding...
dus het antwoord is de oplossing van de dv d/dp y(p) = -1/(1-p) y(p).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Beetje creatief knutselen met de geometrische rij, wat gebeurt er als je de identiteit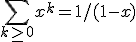 
differentieert naar x?
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Dit klopt toch niet? Je vergeet een factor (k-2) bij het differentiëren naar p van de termen van de reeks en tevens is k(k2) = (k3 - k2)/2.quote:
wat een naar ding...
dus het antwoord is de oplossing van de dv d/dp y(p) = -1/(1-p) y(p).
[ Bericht 1% gewijzigd door Riparius op 24-09-2011 19:36:07 ]
Ik denk dat je beter die geometrische som kunt gebruiken, dat zal ook wel de bedoeling van de opgave zijn denk ik.quote:
Glowmouse, ik zie niet waar je die [k^3-k] / 2 vandaan haalt.
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Als je die differentiëert krijg je trouwensquote:
[..]
Ik denk dat je beter die geometrische som kunt gebruiken, dat zal ook wel de bedoeling van de opgave zijn denk ik.
Maar ik weet niet echt wat ik met dat binomiaalcoëfficiënt aanmoet...
(k2) = k(k-1)/2, dus k(k2) = (k3 - k2)/2. Maar de oplossing van Glowmouse klopt niet, ook al niet omdat hij een factor (k-2) vergeet.quote:
Glowmouse, ik zie niet waar je die [k^3-k] / 2 vandaan haalt.
Met de k in de som bedoel je? Als je nu gebruikt datquote:
[..]
Als je die differentiëert krijg je trouwens
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Pff dat is nog een heel karwei. Je krijgt dan uiteindelijk een DV die je moet oplossen? Met de afgeleide van de rechterkant van die identiteit is vast makkelijker.quote:
[..]
Met de k in de som bedoel je? Als je nu gebruikt dat, dan kun je jouw som in delen schrijven die allemaal uit te drukken zijn als de eerste/tweede/... afgeleide van
en kun je op die manier een uitdrukking voor jouw som vinden.
Zo'n gedoe voor een vraag uit de kansrekening, dat had ik niet verwacht
.
Vind je? Lees eens wat werk van Leonard Euler, dat was een absolute virtuoos op het gebied van het manipuleren van oneindige reeksen en dan zie je pas echt dingen waar je perplex van staat.quote:
[..]
Pff dat is nog een heel karwei.
Is toch een mooie uitdaging?quote:Zo'n gedoe voor een vraag uit de kansrekening, dat had ik niet verwacht
Bekijk het eens als volgt (met dank aan keesjeislief). Beschouw een reeks waarvan de termen van de gedaante
(1) (1 - p)k+1
zijn, en waarbij je k laat lopen van 2 tot ∞. Merk trouwens op dat deze reeks alleen convergent is voor |1 - p| < 1. Deze meetkundige reeks kun je gemakkelijk sommeren en daarmee uitdrukken in p. Neem nu van beide zijden van je identiteit de afgeleide naar p, dan zijn de termen van de nieuwe reeks te schrijven als:
(2) -k(1 - p)k - (1 - p)k
De som van de deeltermen van de gedaante (1 - p)k kun je gemakkelijk uitdrukken in p, dit is namelijk gelijk aan de som van de termen van de gedaante (1) gedeeld door (1 - p). Met deze gegevens kun je ook de som van deeltermen van (2) van de gedaante k(1 - p)k uitdrukken in p. Nu weer van (2) de afgeleide naar p nemen, dus de tweede afgeleide naar p van (1), en we krijgen
(3) k2(1 - p)k-1 + k(1 - p)k-1
We hebben al een uitdrukking in p voor de som van de termen van (3), namelijk de afgeleide naar p van de som van de termen van de gedaante (2), en aangezien de som van de deeltermen van (3) van de gedaante k(1 - p)k-1 gelijk is aan de eerder bepaalde som van de termen van de gedaante k(1 - p)k gedeeld door (1 - p) kunnen we met deze gegevens weer een uitdrukking in p voor de som van de deeltermen van (3) van de gedaante k2(1 - p)k-1 afleiden. Nu weer (3) differentiëren naar p en we krijgen een uitdrukking die we kunnen schrijven als:
(4) -k2(k - 1)(1 - p)k-2 - k2(1 - p)k-2 + k(1 - p)k-2
De som van de termen van de gedaante (4) uitgedrukt in p is bekend, want dit is de derde afgeleide van (1), en de som van de deeltermen van (4) van de gedaante k2(1 - p)k-2 en k(1 - p)k-2 kunnen we weer uitdrukken in p door de eerder gevonden uitdrukkingen in p voor de sommen van termen van de gedaantes k2(1 - p)k-1 resp. k(1 - p)k-1 te delen door (1 - p). En daarmee zijn we dan in staat om de som van de deeltermen van (4) van de gedaante k2(k - 1)(1 - p)k-2 uit te drukken in p. De gevraagde som van de reeks bestaande uit termen van de gedaante k(k2)(1 - p)k-2 is uiteraard de helft daarvan.
[ Bericht 0% gewijzigd door Riparius op 24-09-2011 21:30:39 ]
je hebt gelijkquote:
[..]
Dit klopt toch niet? Je vergeet een factor (k-2) bij het differentiëren naar p van de termen van de reeks en tevens is k(k2) = (k3 - k2)/2.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Bewering: U1 en U2 deelruimtes van vectorruimte V, dan
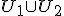is ook een deelruimte van V desda 
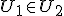of 
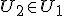
Aantonen dat de vereniging een deelruimte is als die voorwaarde geldt lukt me. Andersom niet.
Voor alle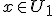
en alle 
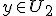geldt dat de som van x en y in de vereniging van U1 en U2 zit. Hoe kan ik daaruit concluderen dat 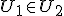of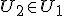
? Ik heb geprobeerd aan te nemen dat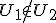
of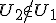 
en dan tegenspraak proberen te vinden, maar daar kom ik niet uit.
Aantonen dat de vereniging een deelruimte is als die voorwaarde geldt lukt me. Andersom niet.
Voor alle
? Ik heb geprobeerd aan te nemen dat
Latex tip: \subsetquote:
Bewering: U1 en U2 deelruimtes van vectorruimte V, dan
Aantonen dat de vereniging een deelruimte is als die voorwaarde geldt lukt me. Andersom niet.
Voor alle
? Ik heb geprobeerd aan te nemen dat
Als het niet geldt, dan is er een x in U1-U2 en een y in U2-U1. Nu jij weer.
Dat betekent meteen dat x + y niet in de vereniging van U1 en U2 zit, dus tegenspraak?
(edit)Nee dat klopt niet
Dus x + y >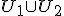
[ Bericht 27% gewijzigd door Anoonumos op 25-09-2011 14:38:37 ]
(edit)Nee dat klopt niet
Dus x + y >
[ Bericht 27% gewijzigd door Anoonumos op 25-09-2011 14:38:37 ]
Het zit in de een, of in de ander (of beide).
Dus x + y zit niet in U1, niet in U2, dus ook niet in U1verenigdU2.
Dus x + y zit niet in U1, niet in U2, dus ook niet in U1verenigdU2.
