SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Laatste post:
maar zo:
= 1000 + 300x + 300 + x2 + 1 - 1000 + 300x - x2
= 600x + 301
edit: nu zal ik wel delen moeten door 300 oid, maar hoe kom ik daar aan?
Niet zo = 1000 + 300x + 300 + x2 + 1 - 1000 + 300x + x2quote:Op dinsdag 13 september 2011 12:09 schreef Haushofer het volgende:
[..]
Je hebt een tekenfout gemaakt bij de laatste x2; dit moet -x2 zijn, zoals ik heb gequote.
maar zo:
= 1000 + 300x + 300 + x2 + 1 - 1000 + 300x - x2
= 600x + 301
edit: nu zal ik wel delen moeten door 300 oid, maar hoe kom ik daar aan?
Je vraag is onduidelijk.quote:
Ik zie het niet, maar waarom geldt deze vergelijking niet met x,y in het open interval (0,1) :
1-x-y+2xy=0
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik moet laten zien dat voor alle x en y in het interval (0,1) de functiequote:
1-x-y+2xy
ongelijk aan 0 is.
Zie dat je nog een tekenfout hebt gemaaktquote:
Laatste post:
[..]
Niet zo = 1000 + 300x + 300 + x2 + 1 - 1000 + 300x + x2
maar zo:
= 1000 + 300x + 300 + x2 + 1 - 1000 + 300x - x2
= 600x + 301
edit: nu zal ik wel delen moeten door 300 oid, maar hoe kom ik daar aan?
Dit soort opgaven kun je het beste doen met haakjes.Nu zie je dat veel tegen elkaar wegvalt:
-
awesome!quote:
[..]
Zie dat je nog een tekenfout hebt gemaakt
thanks.
Ik denk vrij zeker te weten dat ze willen dat ik het probeer te bewijzen met inductie en bij andere vragen snap ik wel hoe dat werkt, maar hier heb ik geen idee hoe te beginnen.. Iemandquote:Claim: "For a ∈ ℕ, a² is a multiple of 7 ⇒ a is a multiple of 7. "
Is this claim correct? Explain the answer.
?
Özil | Ki SY| Son HM| Lee SW| Taeguk Warriors|
Lijkt me vrij eenvoudig zonder inductie. Als a namelijk geen priemfactor 7 heeft, dan kan a2 dat ook niet hebben. Ergo, als a2 wel deelbaar is door 7, dan moet a ook deelbaar zijn door 7.quote:
[..]
Ik denk vrij zeker te weten dat ze willen dat ik het probeer te bewijzen met inductie en bij andere vragen snap ik wel hoe dat werkt, maar hier heb ik geen idee hoe te beginnen.. Iemand
syntax =~ is "benaderd door"
Ik heb moeite met het begrijpen van de volgende opgave:
Establish the approximation
dit hoort geen = teken te zijn, meer een =~, maar ik weet niet hoe wolfram precies werkt. Sowieso vind ik het een rare opdracht aangezien er nergens staat wat de variabelen of constanten zijn, maar ik neem maar aan dat ze t als variabel bedoelen.
De paragraaf waarbij deze opdracht staat is de Taylor formule.
Er staat ook dat in het geval dat een approximation nabij x = 0 en f(x) = e^x dan:
e^x =~ 1 + x/1! + x^2/2! ..enzovoort
Dit begrijp ik, omdat de nde afgeleide steeds e^x is en dus nabij x = 0 steeds 1 is
,zodoende hou je alleen de x'en over.
--
Nu heeft de docent bij de opdracht gezet: Tip gebruik x = o*sqrt(t/n)
Zo gezegd zo gedaan, als je in de hierboven genoemde reeks x = o*sqrt(t/n) invult dan krijg je inderdaad de approximation 1 + o*sqrt(t/n) + o^2*t/(2n)
Nu begrijp ik alleen niet waarom dit trucje werkt, waarom je o*sqrt(t/n) gewoon mag vervangen door x.
Als je deze approximation gewoon via de Taylor formule, en n = 2 (quadratisch), zou proberen te benaderen lijkt mij dat er een hele andere formule uitkomt.
Taylor formule:
f'(a) = afgeleide van f(t) op het punt a.
f''(a) = tweede afgeleide
f(a) + f'(a)*(t-a) + f''(a)*(t-a)^2
f(t) = e^(o*sqrt(t/n))
f(a) = 1
f'(t) =
f''(t) =
Op a = 0 dan krijg je dus
f'(a) = Error? Je mag niet delen door 0?
f''(a) = error? je mag niet delen door 0?
Ik kom er dus niet echt uit op deze manier.
edit, plaatjes en wat dingen herschreven.
[ Bericht 1% gewijzigd door JohnSpek op 13-09-2011 17:02:05 ]
Ik heb moeite met het begrijpen van de volgende opgave:
Establish the approximation
dit hoort geen = teken te zijn, meer een =~, maar ik weet niet hoe wolfram precies werkt. Sowieso vind ik het een rare opdracht aangezien er nergens staat wat de variabelen of constanten zijn, maar ik neem maar aan dat ze t als variabel bedoelen.
De paragraaf waarbij deze opdracht staat is de Taylor formule.
Er staat ook dat in het geval dat een approximation nabij x = 0 en f(x) = e^x dan:
e^x =~ 1 + x/1! + x^2/2! ..enzovoort
Dit begrijp ik, omdat de nde afgeleide steeds e^x is en dus nabij x = 0 steeds 1 is
,zodoende hou je alleen de x'en over.
--
Nu heeft de docent bij de opdracht gezet: Tip gebruik x = o*sqrt(t/n)
Zo gezegd zo gedaan, als je in de hierboven genoemde reeks x = o*sqrt(t/n) invult dan krijg je inderdaad de approximation 1 + o*sqrt(t/n) + o^2*t/(2n)
Nu begrijp ik alleen niet waarom dit trucje werkt, waarom je o*sqrt(t/n) gewoon mag vervangen door x.
Als je deze approximation gewoon via de Taylor formule, en n = 2 (quadratisch), zou proberen te benaderen lijkt mij dat er een hele andere formule uitkomt.
Taylor formule:
f'(a) = afgeleide van f(t) op het punt a.
f''(a) = tweede afgeleide
f(a) + f'(a)*(t-a) + f''(a)*(t-a)^2
f(t) = e^(o*sqrt(t/n))
f(a) = 1
f'(t) =
f''(t) =
Op a = 0 dan krijg je dus
f'(a) = Error? Je mag niet delen door 0?
f''(a) = error? je mag niet delen door 0?
Ik kom er dus niet echt uit op deze manier.
edit, plaatjes en wat dingen herschreven.
[ Bericht 1% gewijzigd door JohnSpek op 13-09-2011 17:02:05 ]
Lijkt me niet zo moeilijk als je het meetkundig bekijkt. De grafiek van 1 - x - y +2xy = 0 is een hyperbool die geen punten heeft in het gebied G := {(x;y) ∈ R2 | 0 < x < 1 ∧ 0 < y < 1}.quote:
[..]
Ik moet laten zien dat voor alle x en y in het interval (0,1) de functie
1-x-y+2xy
ongelijk aan 0 is.
Ik begrijp je probleem niet zo. De Taylorreeks voor ex is geldig (convergent) voor elke reële (en trouwens ook complexe) x en dus kun je hierin x = o∙√(t/n) substitueren, mits t ≥ 0. Je vergeet kennelijk alleen dat o∙√(t/n) niet differentieerbaar is naar t bij t = 0.quote:
syntax =~ is "benaderd door"
Ik heb moeite met het begrijpen van de volgende opgave:
Establish the approximation [ afbeelding ]
dit hoort geen = teken te zijn, meer een =~, maar ik weet niet hoe wolfram precies werkt. Sowieso vind ik het een rare opdracht aangezien er nergens staat wat de variabelen of constanten zijn, maar ik neem maar aan dat ze t als variabel bedoelen.
De paragraaf waarbij deze opdracht staat is de Taylor formule.
Er staat ook dat in het geval dat een approximation nabij x = 0 en f(x) = e^x dan:
e^x =~ 1 + x/1! + x^2/2! ..enzovoort
Dit begrijp ik, omdat de nde afgeleide steeds e^x is en dus nabij x = 0 steeds 1 is
,zodoende hou je alleen de x'en over.
--
Nu heeft de docent bij de opdracht gezet: Tip gebruik x = o*sqrt(t/n)
Zo gezegd zo gedaan, als je in de hierboven genoemde reeks x = o*sqrt(t/n) invult dan krijg je inderdaad de approximation 1 + o*sqrt(t/n) + o^2*t/(2n)
Nu begrijp ik alleen niet waarom dit trucje werkt, waarom je o*sqrt(t/n) gewoon mag vervangen door x.
Als je deze approximation gewoon via de Taylor formule, en n = 2 (quadratisch), zou proberen te benaderen lijkt mij dat er een hele andere formule uitkomt.
Taylor formule:
f'(a) = afgeleide van f(t) op het punt a.
f''(a) = tweede afgeleide
f(a) + f'(a)*(t-a) + f''(a)*(t-a)^2
f(t) = e^(o*sqrt(t/n))
f(a) = 1
f'(t) = [ afbeelding ]
f''(t) = [ afbeelding ]
Op a = 0 dan krijg je dus
f'(a) = Error? Je mag niet delen door 0?
f''(a) = error? je mag niet delen door 0?
Ik kom er dus niet echt uit op deze manier.
edit, plaatjes en wat dingen herschreven.
2xy=x+y-1, linkerkant >0 dus x+y>1.quote:
[..]
Ik moet laten zien dat voor alle x en y in het interval (0,1) de functie
1-x-y+2xy
ongelijk aan 0 is.
y(2x-1)=x-1, rechterkant <0 dus 2x-1<0 dus x<0.5
x(2y-1)=y-1, rechterkant <0 dus 2y-1<0 dus y<0.5
1<x+y<0.5+0.5<1
Ik vraag mij af waarom dat zo is, aangezien het invullen van de Taylorreeks met deze functie niet kan omdat, zoals je zegt, de functie niet differentieerbaar is nabij nul.quote:
[..]
Ik begrijp je probleem niet zo. De Taylorreeks voor ex is geldig (convergent) voor elke reële (en trouwens ook complexe) x en dus kun je hierin x = o∙√(t/n) substitueren, mits t ≥ 0. Je vergeet kennelijk alleen dat o∙√(t/n) niet differentieerbaar is naar t bij t = 0.
De Taylorreeks voor ex blijft gewoon een convergente reeks door de substitutie x = o∙√(t/n) (t ≥ 0). Maar dan is het geen Taylorreeks meer, want eo∙√(t/n) druk je dan niet uit als een machtreeks met gehele machten van je variabele t. En dus hoeft de functie ook niet differentieerbaar te zijn bij t = 0.quote:
[..]
Ik vraag mij af waarom dat zo is, aangezien het invullen van de Taylorreeks met deze functie niet kan omdat, zoals je zegt, de functie niet differentieerbaar is nabij nul.
Maar het gaat bijvoorbeeld niet op voor deze e (als ik het goed bereken)quote:
[..]
De Taylorreeks voor ex blijft gewoon een convergente reeks door de substitutie x = o∙√(t/n) (t ≥ 0). Maar dan is het geen Taylorreeks meer, want eo∙√(t/n) druk je dan niet uit als een machtreeks met gehele machten van je variabele t. En dus hoeft de functie ook niet differentieerbaar te zijn bij t = 0.
e^(3t+5) , ik neem x = 3t +5
Dat zou volgens de reeks voor e^x, met n is 2, 1 + x/1 + x^2/2! wordt dan..
1 + (3t+5) + (9t^2 + 25 + 6t)/2
Stel ik doe het via de taylorreeks
f(t) = e^(3t+5)
f'(t) = 3*e^(3t+5)
f''(t) = 9*e^(3t+5)
Dat zou het benaderd bij a = 0 zijn volgens de taylorreeks:
1 + 3*e^(3a+5)*(t) + (9*e^(3a+5)*t^2)/2 =
1 + 3*e^(3*0+5)*t + (9*e^(3*0+5)*t^2)/2
= 1 + 3*(e^5)*t + (9*(e^5)*t^2)/2
Dit is een hele andere formule.
Is het zo dat de truc van het simpelweg substituten door x alleen goed gaat als e^(x) uitkomt op e^(0) als je nul invoert voor t?
Je redenering gaat niet op omdat je alleen de eerste paar termen vergelijkt van twee oneindige reeksen die convergeren naar dezelfde waarde. Het feit dat ze allebei een benadering leveren van eenzelfde functie betekent niet dat die benaderingen ook identiek zijn, en dat zijn ze hier dan ook niet. En wat je met die 'truc' bedoelt begrijp ik niet, maar in ieder geval klopt het niet. Immers in je voorbeeld hierboven is toch ook x = 0 voor t = 0.quote:
[..]
Maar het gaat bijvoorbeeld niet op voor deze e (als ik het goed bereken)
e^(3t+5) , ik neem x = 3t +5
Dat zou volgens de reeks voor e^x, met n is 2, 1 + x/1 + x^2/2! wordt dan..
1 + (3t+5) + (9t^2 + 25 + 6t)/2
Stel ik doe het via de taylorreeks
f(t) = e^(3t+5)
f'(t) = 3*e^(3t+5)
f''(t) = 9*e^(3t+5)
Dat zou het benaderd bij a = 0 zijn volgens de taylorreeks:
1 + 3*e^(3a+5)*(t) + (9*e^(3a+5)*t^2)/2 =
1 + 3*e^(3*0+5)*t + (9*e^(3*0+5)*t^2)/2
= 1 + 3*(e^5)*t + (9*(e^5)*t^2)/2
Dit is een hele andere formule.
Is het zo dat de truc van het simpelweg substituten door x alleen goed gaat als e^(x) uitkomt op e^(0) als je nul invoert voor t?
als x = 3t + 5, als t = 0 , dan is x = 5. Dat bedoelde ik.quote:
[..]
Je redenering gaat niet op omdat je alleen de eerste paar termen vergelijkt van twee oneindige reeksen die convergeren naar dezelfde waarde. Het feit dat ze allebei een benadering leveren van eenzelfde functie betekent niet dat die benaderingen ook identiek zijn, en dat zijn ze hier dan ook niet. En wat je met die 'truc' bedoelt begrijp ik niet, maar in ieder geval klopt het niet. Immers in je voorbeeld hierboven is toch ook x = 0 voor t = 0.
Ik denk dat ik in de war ben omdat de serie van e wordt afgeleid van de taylor reeks in het boek.
f(x) = e^x
f'(x) = e^x
f''(x) = e^x
....
fn(x) = e^x
Dan vullen ze dit in de taylor reeks in, en dan komt de reeks uit op e =~ 1 + 1/x + x^2/2! + x^3/3! + .... + x^n/n!
Ik ging er dus vanuit dat sinds de e serie van de taylorreeks kwam, als je bijvoorbeeld e^(3t+5) invult in de 2 reeksen, dat je dan ook hetzelfde antwoord zou krijgen. Maar beide zijn dus valide kwadratische benaderingen voor deze functie?
[ Bericht 8% gewijzigd door JohnSpek op 13-09-2011 19:00:05 ]
f(x) = e^x
f'(x) = e^x
f''(x) = e^x
....
fn(x) = e^x
Dan vullen ze dit in de taylor reeks in, en dan komt de reeks uit op e =~ 1 + 1/x + x^2/2! + x^3/3! + .... + x^n/n!
Ik ging er dus vanuit dat sinds de e serie van de taylorreeks kwam, als je bijvoorbeeld e^(3t+5) invult in de 2 reeksen, dat je dan ook hetzelfde antwoord zou krijgen. Maar beide zijn dus valide kwadratische benaderingen voor deze functie?
[ Bericht 8% gewijzigd door JohnSpek op 13-09-2011 19:00:05 ]
Nee, want je vergeet dat de andere termen (3t + 5)n/n! met n > 2 ook een bijdrage leveren met t2.quote:
Ik ging er dus vanuit dat sinds de e serie van de taylorreeks kwam, als je bijvoorbeeld e^(3t+5) invult in de 2 reeksen, dat je dan ook hetzelfde antwoord zou krijgen. Maar beide zijn dus valide kwadratische benaderingen voor deze functie?
Handig die TeX math mogelijkheid bij FOK!.
Vroeger zat Iblis wel eens hier om te helpen met wiskunde opdrachten (in mijn studietijd).
Nu zie ik hem echter nooit meer. Waar is hij gebleven?
Vroeger zat Iblis wel eens hier om te helpen met wiskunde opdrachten (in mijn studietijd).
Nu zie ik hem echter nooit meer. Waar is hij gebleven?
kloep kloep
Jammer, was toffe gast hier. Hulpvaardig met name. Dus hij is ineens zonder opgaaf van reden verdwenen?
kloep kloep
Inderdaad. Hij was ook vrij anoniem, dus het is voor zover ik weet niet eens bekend of hij nog leeft.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
...wow... moest vanavond ineens aan hem denken...hij heeft mij indertijd best veel geholpen.
Geen enkele user is ook verplicht om aan te geven waarom hij/zij niet meer komt.
Dat hij niet meer zou leven is natuurlijk speculatie, maar aan de andere kant verwacht je ook niet dat iemand die veel op dit forum zit het ineens volkomen de rug toekeert. Ik wens hem het beste toe.
Geen enkele user is ook verplicht om aan te geven waarom hij/zij niet meer komt.
Dat hij niet meer zou leven is natuurlijk speculatie, maar aan de andere kant verwacht je ook niet dat iemand die veel op dit forum zit het ineens volkomen de rug toekeert. Ik wens hem het beste toe.
kloep kloep
Hij had duidelijk een internetverslaving. Ik ga er vooralsnog van uit dat hij cold turkey is gegaan. Maar ook dat is speculatie. .
.
RIP aan deze LaTeX baasquote:Op woensdag 14 september 2011 20:29 schreef GlowMouse het volgende:
Inderdaad. Hij was ook vrij anoniem, dus het is voor zover ik weet niet eens bekend of hij nog leeft.
Vraagje: Welke regel moet ik hier toepassen, ik moet 
oplossen..
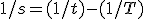
Als ik de noemer gelijk maak krijg ik:
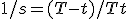
Maar hoe krijg ik in de laatste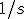
, 1/ weg..Mag ik het gewoon omdraaien?
Als ik de noemer gelijk maak krijg ik:
Maar hoe krijg ik in de laatste
Inzicht is beter dan regeltjes leren over wat 'mag' en 'niet mag'. Als je hebt:quote:
Vraagje: Welke regel moet ik hier toepassen, ik moet
Als ik de noemer gelijk maak krijg ik:
Maar hoe krijg ik in de laatste
1/p = 1/q,
waarbij we p en q beiden ongelijk aan nul veronderstellen, omdat de breuken anders geen betekenis hebben, en we vermenigvuldigen beide leden met het product pq, dan krijgen we:
pq/p = pq/q.
Nu is de breuk in het linkerlid te vereenvoudigen tot q/1 = q omdat teller en noemer een factor p gemeen hebben, en de breuk in het rechterlid is te vereenvoudigen tot p/1 = p omdat teller en noemer een factor q gemeen hebben. En dus resulteert inderdaad q = p oftewel p = q.
Ben even de weg kwijt, wie helpt?
De integraal van p(x) = A e^(-lamda(x-a)^2)
Moet ik de vermenigvuldiging in de e-macht (x-a)^2 eerst uitwerken naar x^2 -2ax+a^2 en dan de e-macht opdelen in verschillende stukken, los integreren en dan samenvoegen? Of is er een makkelijkere oplossing...
En sowieso.. wat was de integraal van e^(x^2) ook alweer?
De integraal van p(x) = A e^(-lamda(x-a)^2)
Moet ik de vermenigvuldiging in de e-macht (x-a)^2 eerst uitwerken naar x^2 -2ax+a^2 en dan de e-macht opdelen in verschillende stukken, los integreren en dan samenvoegen? Of is er een makkelijkere oplossing...
En sowieso.. wat was de integraal van e^(x^2) ook alweer?
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.
Je kunt gebruiken datquote:
Ben even de weg kwijt, wie helpt?
De integraal van p(x) = A e^(-lamda(x-a)^2)
Moet ik de vermenigvuldiging in de e-macht (x-a)^2 eerst uitwerken naar x^2 -2ax+a^2 en dan de e-macht opdelen in verschillende stukken, los integreren en dan samenvoegen? Of is er een makkelijkere oplossing...
En sowieso.. wat was de integraal van e^(x^2) ook alweer?
voor elke
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Sorry ik was vergeten te vermelden dat ik dan wil integreren van -oneindig tot +oneindig
Dank keesjeislief!
Dank keesjeislief!
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.
Ik zal wel een kneus zijn... maar als ik nu <x> wil berekenen, dus de integraal over -oneindig tot +oneindig van x*p(x) dx met p(x)=A e^(-lamda(x-a)^2), hoe doe ik dat dan?
voelt zich geen wiskundig wonder
voelt zich geen wiskundig wonder
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.
Substitutie: noem u = -\lambda(x-a)^2, dan du -2\lambda(x-a) dx.
Dit kun je altijd doen als de macht van x in de exponent 1 hoger is dan de macht van x in de integraal
Dit kun je altijd doen als de macht van x in de exponent 1 hoger is dan de macht van x in de integraal
-
Ik vat 'm nog niet helemaal.quote:
[..]
Inzicht is beter dan regeltjes leren over wat 'mag' en 'niet mag'. Als je hebt:
1/p = 1/q,
waarbij we p en q beiden ongelijk aan nul veronderstellen, omdat de breuken anders geen betekenis hebben, en we vermenigvuldigen beide leden met het product pq, dan krijgen we:
pq/p = pq/q.
Nu is de breuk in het linkerlid te vereenvoudigen tot q/1 = q omdat teller en noemer een factor p gemeen hebben, en de breuk in het rechterlid is te vereenvoudigen tot p/1 = p omdat teller en noemer een factor q gemeen hebben. En dus resulteert inderdaad q = p oftewel p = q.
als ik heb 1/s = (T-t)/tT hoe krijg ik dan s = tT/T-t (uit antwoordboek)?
Weet je wat kruiselings vermenigvuldigen is?quote:
[..]
Ik vat 'm nog niet helemaal.
als ik heb 1/s = (T-t)/tT hoe krijg ik dan s = tT/T-t (uit antwoordboek)?
Of:
Weet je waarom je beide kanten met een getal(of letter!) mag vermenigvuldigen?
Via kruislings heb ik hem nu opgelost.. thanks, maar wat bedoel je met dat laatste? * S?quote:
[..]
Weet je wat kruiselings vermenigvuldigen is?
Of:
Weet je waarom je beide kanten met een getal(of letter!) mag vermenigvuldigen?
Jij had de vergelijking:quote:
[..]
Via kruislings heb ik hem nu opgelost.. thanks, maar wat bedoel je met dat laatste? * S?
1/s = (T-t)/tT
Je weet dus dat s,t en T niet nul zijn (waarom?), dus kun je beide kanten bijvoorbeeld met s vermenigvuldigen:
1=s(T-t)/tT
Vermenigvuldig beide kanten nu met tT/(T-t) (of anders gezegd: Deel beide kanten door (T-t)/tT) ,dan krijg je:
tT/(T-t)=s
En dus weet je wat s is.
Je kunt een vergelijking aan beide kanten met een getal/letter vermenigvuldigen zolang het maar niet 0 is. Net zo mag je aan beide kanten iets toevoegen. Denk er maar eens over na, neem de vergelijking :
x=10
Vermenigvuldig beide kanten maar eens met een getal, of tel aan beide kanten iets op. Wat belangrijk is, is dat x daardoor niet verandert! Dat gebeurt wel als je die vermenigvuldiging of optelling maar aan één kant doet. Dat is ook logisch:
x=10 en niet x=10+2 of x-3=10.
En dit kun je dus met elke vergelijking doen.
volgende som (sqrt in een sqrt) staat gelijk aan C.
1....
1+R - A ............ = C
1....
1+R + B
Hoe krijg ik R hieruit? (let niet op de puntjes)
wat heb ik tot dusverre geprobeert:
A/B = C » A = C
A/B - C = 0 en dan verder uitwerken (kom ik ook niet verder)
A/B * B = C*B » A = CB kump ik ook niet verder
1....
1+R - A ............ = C
1....
1+R + B
Hoe krijg ik R hieruit? (let niet op de puntjes)
wat heb ik tot dusverre geprobeert:
A/B = C » A = C
A/B - C = 0 en dan verder uitwerken (kom ik ook niet verder)
A/B * B = C*B » A = CB kump ik ook niet verder
Amen... ik blijf dit soort dingen lastig vinden... practice makes perfect I guess.quote:
Substitutie: noem u = -\lambda(x-a)^2, dan du -2\lambda(x-a) dx.
Dit kun je altijd doen als de macht van x in de exponent 1 hoger is dan de macht van x in de integraal
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.
Weet iemand toevallig hoe ik deze recursieve definitie om kan schrijven naar een directe formule? Het is een beetje weggezakt, en een huisgenoot doet een één of ander bedrijfskundevak waar 't relevant is. Met een recursief programma kan ik 't nog wel oplossen bij n = 40, maar met het handje op 't tentamen is 't nogal wat werk..
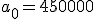
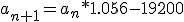
Dit is de opgave toch?quote:Op donderdag 15 september 2011 17:48 schreef Sokz het volgende:
volgende som (sqrt in een sqrt) staat gelijk aan C.
1....
1+R - A ............ = C
1....
1+R + B
Hoe krijg ik R hieruit? (let niet op de puntjes)
wat heb ik tot dusverre geprobeert:
A/B = C » A = C
A/B - C = 0 en dan verder uitwerken (kom ik ook niet verder)
A/B * B = C*B » A = CB kump ik ook niet verder
Eerst vermenigvuldigen we dan de teller en de noemer met 1+R:
Dan vermenigvuldigen we links en rechts met 1+B+BR:
Dan halen we de termen met R naar een kant:
Dan halen we R buiten haakjes:
En dan delen we door BC+A
The biggest argument against democracy is a five minute discussion with the average voter.
Hee jongens, ik heb weer een vraag
Kan iemand mij helpen met dit?
Bepaal de inverse functie van
N = f(L) = 1
Hoe zoek ik dan uit wat L is?
Kan iemand mij helpen met dit?
Bepaal de inverse functie van
N = f(L) = 1
Hoe zoek ik dan uit wat L is?
In het algemeen:quote:
Weet iemand toevallig hoe ik deze recursieve definitie om kan schrijven naar een directe formule? Het is een beetje weggezakt, en een huisgenoot doet een één of ander bedrijfskundevak waar 't relevant is. Met een recursief programma kan ik 't nog wel oplossen bij n = 40, maar met het handje op 't tentamen is 't nogal wat werk..
Stel a0 = b en an+1 = c an + d.
Dan krijg je dus
a1 = c a0 + d = cb + d
a2 = c a1 + d = c(cb+d) + d = c²b + cd + d
a3 = c a2 + d = c(c(cb+d)+d) + d = c³b + c² d + cd + d
Aan het patroon zie je dat je dan krijgt
an = cn b + cn-1 d + ... + c1d + d
Wat is f, wat is L, wat is N?quote:Op donderdag 15 september 2011 19:31 schreef Snuf. het volgende:
Hee jongens, ik heb weer een vraag
Kan iemand mij helpen met dit?
Bepaal de inverse functie van
N = f(L) = 1
Hoe zoek ik dan uit wat L is?
quote:
[..]
Dit is de opgave toch?
Eerst vermenigvuldigen we dan de teller en de noemer met 1+R:
Dan vermenigvuldigen we links en rechts met 1+B+BR:
Dan halen we de termen met R naar een kant:
Dan halen we R buiten haakjes:
En dan delen we door BC+A
Daar was ik me van bewust (met een sigmanotatie is het nog best overzichtelijk) maar dat lost het probleem nog niet op: n = 40 zonder grafische rekenmachine / computerquote:
[..]
In het algemeen:
Stel a0 = b en an+1 = c an + d.
Dan krijg je dus
a1 = c a0 + d = cb + d
a2 = c a1 + d = c(cb+d) + d = c²b + cd + d
a3 = c a2 + d = c(c(cb+d)+d) + d = c³b + c² d + cd + d
Aan het patroon zie je dat je dan krijgt
an = cn b + cn-1 d + ... + c1d + d
Jawel, want je kunt de som van een meetkundige reeks makkelijk berekenen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
