SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Vervang x door -y-zquote:Op zondag 15 mei 2011 21:32 schreef thenxero het volgende:
Als X,Y,Z i.i.d. N(0,1) verdeeld zijn, hoe vind ik dan de verdeling van X▓ + Y▓ + Z▓ | X + Y + Z = 0?
Ik weet dat X▓ + Y▓ + Z▓ chi-kwadraat verdeeld is met drie vrijheidsgraden, kan ik daar iets mee?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik ben gewoon dom bezig, ik probeer een deel van de functie ipv een gebied/D te beschrijven. Wat nergens op slaat of in ieder geval niet handig is.quote:Op maandag 16 mei 2011 16:17 schreef Riparius het volgende:
[..]
Dat is zo niet te beantwoorden, je geeft je nieuwe integratiegrenzen namelijk niet. Maar met poolco÷rdinaten gaan integreren over een vierkant? Dan moet je eerst maar eens uitvogelen hoe je dan r als functie van θ beschrijft voor de beide zijden van het vierkant die niet langs de co÷rdinaatassen liggen. Dan moet je dus eerst vergelijkingen in poolco÷rdinaten gaan opstellen voor de rechte lijnen met de cartesische vergelijkingen x=1 en y=1 en dan moet je alsnog gaan opsplitsen in twee integralen met resp. 0 ≤ θ ≤ π/4 en π/4 ≤ θ ≤ π/2.


Als je zo je cilindercoordinaten kiest is dat equivalent met een integraal over het gebied dat voldoet aanquote:Op maandag 16 mei 2011 16:11 schreef Siddartha het volgende:
[..]
'Binnenste' integraal van 0 naar r, buitenste integraal van 0 naar 2Pi.
en dat is iets anders dan een vierkant.


Ik ben even de weg kwijt... wie kan mij een aanwijzing geven hoe dit op te lossen? Volgens mijn boek moet ik de formules sin2 x + cos2 x = 1 en sin x/cos x = tan x gebruiken, maar daar kom ik niet verder mee. Alvast bedankt voor alle hulp!
quote:Los algebra´sch op: cos2 x = sin x
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


die tweede formule heb je niet eens nodig.. Schrijf de cosinus om in een sinus met behulp van de eerste regel en je krijgt een vergelijking in termen van sinussen die prima op te lossen is met een schaduwvergelijking.
edit: je kan ook alleen de tweede regel gebruiken en sin(x) = tan(x)*cos(x) schrijven, dan staat er aan beide kanten een factor cos(x) in die je buiten haakjes kan halen.
edit: je kan ook alleen de tweede regel gebruiken en sin(x) = tan(x)*cos(x) schrijven, dan staat er aan beide kanten een factor cos(x) in die je buiten haakjes kan halen.


Gebruik de 1e formule en herleid op 0. Vervang dan sin x door een letter.
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Eens kijken of ik het nu beter begrijp:
Ik heb de functie f(x,y)= 1/(x2+y2)2
met gebied D={(x,y)| x2+y2<=1, x+y>=1}
Kan ik dan de twee eisen als volgt weergeven:
(1) x2+y2<=1 word x=rcos(a), y=rsin(a) met grenzen [0,2Pi]
en
(2) x+y>=1 als een x simpel gebied zien: x=L(y)=1-y.
Waarmee ik de dubbele integraal kan bepalen door er twee dubbele integralen van te maken en die van elkaar af te trekken? Dus de dubbele integraal over gebied (1) min de dubbele integraal over gebied (2)?
Ik heb de functie f(x,y)= 1/(x2+y2)2
met gebied D={(x,y)| x2+y2<=1, x+y>=1}
Kan ik dan de twee eisen als volgt weergeven:
(1) x2+y2<=1 word x=rcos(a), y=rsin(a) met grenzen [0,2Pi]
en
(2) x+y>=1 als een x simpel gebied zien: x=L(y)=1-y.
Waarmee ik de dubbele integraal kan bepalen door er twee dubbele integralen van te maken en die van elkaar af te trekken? Dus de dubbele integraal over gebied (1) min de dubbele integraal over gebied (2)?


Als je cartesische co÷rdinaten transformeert naar poolco÷rdinaten, dan moet je ook voor de beide nieuwe co÷rdinaten (r en θ) de condities aangeven die gelden voor het gebied waarover je wil gaan integreren, en dus niet alleen voor θ.quote:Op maandag 16 mei 2011 16:44 schreef Siddartha het volgende:
Eens kijken of ik het nu beter begrijp:
Ik heb de functie f(x,y)= 1/(x2+y2)2
met gebied D={(x,y)| x2+y2<=1, x+y>=1}
Kan ik dan de twee eisen als volgt weergeven:
(1) x2+y2<=1 word x=rcos(a), y=rsin(a) met grenzen [0,2Pi]
Maak eerst eens een tekening van het bedoelde gebied en bedenk dan hoe je dit in poolco÷rdinaten kunt karakteriseren.quote:en
(2) x+y>=1 als een x simpel gebied zien: x=L(y)=1-y.
Waarmee ik de dubbele integraal kan bepalen door er twee dubbele integralen van te maken en die van elkaar af te trekken? Dus de dubbele integraal over gebied (1) min de dubbele integraal over gebied (2)?


Klopt, r: [0,1].quote:Op maandag 16 mei 2011 16:52 schreef Riparius het volgende:
[..]
Als je cartesische co÷rdinaten transformeert naar poolco÷rdinaten, dan moet je ook voor de beide nieuwe co÷rdinaten (r en θ) de condities aangeven die gelden voor het gebied waarover je wil gaan integreren, en dus niet alleen voor θ.
D is het gebied tussen de cirkel met straal 1 en de lijn die loopt van y=1 tot x=1.quote:Maak eerst eens een tekening van het bedoelde gebied en bedenk dan hoe je dit in poolco÷rdinaten kunt karakteriseren.
Kan ik dan D weergeven door gebied (1) te pakken, maar dan te beperken tot:
a:[0,1/2Pi], r:[0,1] ?


Ik heb de oplossing gevonden van de vergelijking. Het was even lastig (aangezien ik niet zo goed ben in oplossen via algebra´sche weg.)
Het volgende heb ik gedaan: Ik heb eerst cosinus herleid naar sinus via de eerste formule. Toen heb ik de formule naar een tweedegraadsvergelijking herleid en hem met behulp van de ABC-formule opgelost. De weg die ik (ongeveer) gevolgd heb:
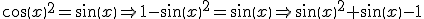
Het volgende heb ik gedaan: Ik heb eerst cosinus herleid naar sinus via de eerste formule. Toen heb ik de formule naar een tweedegraadsvergelijking herleid en hem met behulp van de ABC-formule opgelost. De weg die ik (ongeveer) gevolgd heb:
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Je hebt het rechterlid van je vergelijking wel netjes herleid op nul, maar bent vervolgens die nul weer vergeten, en dat is niet goed want dan is het geen vergelijking meer. De vergelijking die je krijgt is:quote:Op maandag 16 mei 2011 17:29 schreef Pipo1234 het volgende:
Ik heb de oplossing gevonden van de vergelijking. Het was even lastig (aangezien ik niet zo goed ben in oplossen via algebra´sche weg.)
Het volgende heb ik gedaan: Ik heb eerst cosinus herleid naar sinus via de eerste formule. Toen heb ik de formule naar een tweedegraadsvergelijking herleid en hem met behulp van de ABC-formule opgelost. De weg die ik (ongeveer) gevolgd heb:
[ afbeelding ]
sin2x + sin x - 1 = 0
Dit is een kwadratische vergelijking in sin x. Maar nu moet je uiteindelijk hieruit x oplossen. Hoe ben je nu verder gegaan? En wat was je uitkomst? Deze vergelijking komt niet 'mooi' uit.


Mijn oplossing was afgerond 0,67 en 3,81 en dat zijn ook degene die ik zocht. Ik moest er overigens wel nog een aantal dingen mee doen voordat ik op die waarden uitkwam, aangezien de waarden uit een ABC-formule niet direct op x slaan.quote:Op maandag 16 mei 2011 17:35 schreef Riparius het volgende:
[..]
Je hebt het rechterlid van je vergelijking wel netjes herleid op nul, maar bent vervolgens die nul weer vergeten, en dat is niet goed want dan is het geen vergelijking meer. De vergelijking die je krijgt is:
sin2x + sin x - 1 = 0
Dit is een kwadratische vergelijking in sin x. Maar nu moet je uiteindelijk hieruit x oplossen. Hoe ben je nu verder gegaan? En wat was je uitkomst? Deze vergelijking komt niet 'mooi' uit.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Nee, dit klopt niet. In cartesische co÷rdinaten wordt het gebied waarover je wil gaan integreren gekarakteriseerd door:quote:
x2 + y2 ≤ 1 en tevens x + y ≥ 1
Maar dan is het duidelijk dat je r niet over het interval [0,1] kunt nemen. Immers, er ligt geen enkel punt in het bedoelde gebied met r < ½√2.
Nee dus. Stel nu eerst eens een vergelijking in poolco÷rdinaten op van de lijn met de cartesische vergelijking x + y = 1.quote:D is het gebied tussen de cirkel met straal 1 en de lijn die loopt van y=1 tot x=1.
Kan ik dan D weergeven door gebied (1) te pakken, maar dan te beperken tot:
a:[0,1/2Pi], r:[0,1] ?


Daar was ik al bang voor. Je hebt het niet goed gedaan. Je hebt weliswaar de kwadratische vergelijking in sin x opgelost, maar daarmee ben je er nog niet, want x wordt gevraagd, niet sin x. Verder moet je bedenken dat de sinus (voor reŰle x) alleen waarden tussen -1 en +1 aan kan nemen, dus ÚÚn van de beide oplossingen van je vierkantsvergelijking is onbruikbaar.quote:Op maandag 16 mei 2011 17:46 schreef Pipo1234 het volgende:
[..]
Mijn oplossing was afgerond 0,67 en 3,81 en dat zijn ook degene die ik zocht. Ik moest er overigens wel nog een aantal dingen mee doen voordat ik op die waarden uitkwam, aangezien de waarden uit een ABC-formule niet direct op x slaan.


Het is uiteindelijk toch gelukt en ik kwam erop uit dat het chi-kwadraat verdeeld is met twee vrijheidsgraden... de kansdichtheidsfunctie is zeker geen nulquote:Op maandag 16 mei 2011 11:43 schreef Don_Vanelli het volgende:
[..]
hmm.. dit ziet er vreemd uit. X+Y+Z is N(0,3) verdeeld en nu conditioneer je de verdeling van de chi-kwadraatverdeling door deze normale verdeling op nul te stellen. Dat suggereert dat de kansdichtsheidsfunctie van deze verdeling blijkbaar gelijk is aan nul en dan krijg je toch een probleem als je de kansdichtsheidsfunctie van de geconditioneerde verdeling wilt bepalen.


Een schets maken en rechtstreeks de randvoorwaarden invullen geeft eigenlijk al meteen duidelijkheid inderdaad. (iets met een cirkelsegment in het positieve kwadrant)quote:Op maandag 16 mei 2011 17:54 schreef Riparius het volgende:
[..]
Nee, dit klopt niet. In cartesische co÷rdinaten wordt het gebied waarover je wil gaan integreren gekarakteriseerd door:
x2 + y2 ≤ 1 en tevens x + y ≥ 1
Maar dan is het duidelijk dat je r niet over het interval [0,1] kunt nemen. Immers, er ligt geen enkel punt in het bedoelde gebied met r < ½√2.
[..]
Nee dus. Stel nu eerst eens een vergelijking in poolco÷rdinaten op van de lijn met de cartesische vergelijking x + y = 1.


Ik zal je toch maar even op weg helpen, want ik denk dat je de berekening hiervan een beetje onderschat. Ook zie ik dat je steeds probeert om bij het gebied waarover je wil integreren vaste onder- en bovengrenzen te bepalen voor je beide integratievariabelen terwijl dat in zijn algemeenheid niet gaat, ook hier niet.quote:Op maandag 16 mei 2011 16:44 schreef Siddartha het volgende:
Eens kijken of ik het nu beter begrijp:
Ik heb de functie f(x,y)= 1/(x2+y2)2
met gebied D={(x,y)| x2+y2<=1, x+y>=1}
Kan ik dan de twee eisen als volgt weergeven:
(1) x2+y2<=1 word x=rcos(a), y=rsin(a) met grenzen [0,2Pi]
en
(2) x+y>=1 als een x simpel gebied zien: x=L(y)=1-y.
Waarmee ik de dubbele integraal kan bepalen door er twee dubbele integralen van te maken en die van elkaar af te trekken? Dus de dubbele integraal over gebied (1) min de dubbele integraal over gebied (2)?
Laten we eerst eens kijken hoe je de integraal van
(1) f(x,y) = 1/(x2+y2)2
over het gebied
(2) D := {(x;y) ∈ R2 | x2 + y2 ≤ 1 ∧ x + y ≥ 1}
kunt opschrijven in cartesische co÷rdinaten, dus zonder transformatie naar poolco÷rdinaten.
Het gebied D is een cirkelsegment dat, uitgezonderd de beide randpunten (1;0) en (0;1), geheel in het eerste kwadrant ligt en dat wordt begrensd door het deel van de eenheidscirkel dat zich in het eerste kwadrant bevindt en het lijnstuk dat de beide punten (1;0) en (0;1) verbindt.
Als we nu variabele x het interval [0,1] laten doorlopen, dan behoort daarbij voor elke waarde van x uit dit interval een interval voor y waarvan de ondergrens wordt bepaald door de lijn met vergelijking x + y = 1 en de bovengrens door de cirkel met vergelijking x2 + y2 = 1. Aangezien D in het eerste kwadrant ligt geldt hierbij in ieder geval y ≥ 0. Uit x + y = 1 volgt:
(3) y = 1 - x
En uit x2 + y2 = 1 volgt in combinatie met y ≥ 0:
(4) y = √(1 - x2)
Voor elke x zodanig dat 0 ≤ x ≤ 1 is dus 1 - x ≤ y ≤ √(1 - x2), en dus kunnen we het gebied D ook als volgt definiŰren:
(5) D := {(x;y) ∈ R2 | 0 ≤ x ≤ 1 ∧ 1 - x ≤ y ≤ √(1 - x2)}
Kijk voor een plaatje even hier.
De clou is natuurlijk dat we nu de integraal van f(x,y) over D (dankzij het theorema van Fubini) kunnen schrijven als een herhaalde integraal, als volgt:
Ik zou je niet aanraden deze integraal met de hand uit te rekenen. We kunnen de berekening beter hanteerbaar maken door over te gaan op poolco÷rdinaten. Om dit te kunnen doen moeten we eerst het gebied D definiŰren in poolco÷rdinaten, maar dan wel zˇ dat we de integraal van f(x,y) over D weer kunnen schrijven als een herhaalde integraal.
Aangezien het gebied D, uitgezonderd de punten met co÷rdinaten (1;0) en (0;1), geheel in het eerste kwadrant ligt, weten we al dat bij gebruik van poolco÷rdinaten geldt:
(6) 0 ≤ θ ≤ π/2
Maar nu moeten we voor elke waarde van θ op het interval [0, π/2] een onder- en een bovengrens voor r bepalen. Voor de beide punten (1;0) en (0;1) op de rand van D die corresponderen met resp. θ = 0 en θ = π/2 is dit gemakkelijk: hier geldt r = 1, zodat we kunnen zeggen dat de onder- en bovengrens van r hier zijn samengevallen. Maar voor de andere waarden van θ en dus op het open interval (0, π/2) geldt dit niet.
Nemen we bijvoorbeeld θ = π/4, dus precies halverwege het interval [0, π/2], dan zitten we op een lijn die een hoek maakt van 45 graden met de positieve x-as. Dit is uiteraard de lijn met vergelijking x = y, voor zover deze in het eerste kwadrant ligt. Deze lijn snijdt de lijn met vergelijking x + y = 1 in het punt met co÷rdinaten (½;½) en de eenheidscirkel in het punt met co÷rdinaten (½√2;½√2). Het interval waarover r moet lopen voor θ = π/4 wordt nu bepaald door de afstanden tot de oorsprong van deze twee snijpunten.
De bovengrens is eenvoudig, want voor elk punt op de eenheidscirkel is immers r = 1. De bovengrens van het interval waarover r moet lopen voor een gegeven waarde van θ op het interval [0, π/2] ligt dus vast. Maar voor de ondergrens geldt dat niet: de afstand van de oorsprong tot een punt op het lijnstuk dat de punten (0;1) en (0;1) verbindt is variabel en afhankelijk van θ. In het speciale geval θ = π/4 dat we nu bekijken is de afstand van het snijpunt (½;½) tot de oorsprong gelijk aan ½√2, zodat we kunnen concluderen dat voor θ = π/4 geldt ½√2 ≤ r ≤ 1.
Maar dit is niet voldoende: we moeten voor elke waarde van θ op het open interval (0, π/2) de ondergrens van het interval waarover r moet lopen bepalen, in functie van θ. Anders gezegd, we moeten voor elk punt P op het lijnstuk dat de punten met co÷rdinaten (1;0) en (0;1) verbindt de afstand OP = r tot de oorsprong bepalen als functie van de hoek θ die OP maakt met de positieve x-as. Dit betekent niets anders dan dat we een vergelijking in poolco÷rdinaten moeten opstellen van de lijn met de cartesische vergelijking x + y = 1.
Laten we het punt met de co÷rdinaten (1;0) punt A noemen, en zij P een willekeurig punt (anders dan A) op het lijnstuk van A naar het punt (0;1). In driehoek OAP hebben we nu:
(7) ∠AOP = θ en ∠PAO = π/4
En aangezien de som van de hoeken van een driehoek π (radialen) bedraagt, hebben we dus ook:
(8) ∠OPA = π - (π/4 + θ) = ¾π - θ
Volgens de sinusregel hebben we nu in driehoek OAP:
(9) OP : sin ∠PAO = OA : sin ∠OPA
En aangezien OP = r en OA =1 volgt met (7) en (8) dus uit (9) dat:
(10) r : sin(π/4) = 1 : sin(¾π - θ)
En aangezien sin(π/4) = ½√2 hebben we dus:
(11) r = √2/(2∙sin(¾π - θ))
Dit is dus een vergelijking in poolco÷rdinaten van de lijn waarvan de vergelijking in cartesische co÷rdinaten x + y = 1 luidt. Je kunt gemakkelijk nagaan dat voor θ = 0 en θ = π/2 geldt r = 1, terwijl voor θ = π/4 geldt r = ½√2, in overeenstemming met wat we eerder hadden gevonden. Voor het gebied D hebben we nu in poolco÷rdinaten:
(12) 0 ≤ θ ≤ π/2, √2/(2∙sin(¾π - θ)) ≤ r ≤ 1
Nu kunnen we de integraal van f(x,y) = 1/(x2 + y2)2 over D transformeren in een herhaalde integraal in poolco÷rdinaten. We hebben x2 + y2 = r2 en dus 1/(x2 + y2)2 = 1/r4. Bij een variabele substitutie van een integraal in meerdere variabelen moeten we ook nog rekening houden met de determinant van de Jacobiaan, die de schaalfactor geeft voor de transformatie. Bij een transformatie van cartesische co÷rdinaten naar poolco÷rdinaten is dit eenvoudig r, zodat dxdy = dydx vervangen wordt door rdrdθ. We krijgen dan:
Zoals verwacht, is de uitkomst 1/2. Probeer nu zelf deze integraal wel met de hand uit te werken. Als je het goed doet vind je na integratie met r als variabele en na wat goniometrische herleidingen voor de binnenste integraal sin θ∙cos θ, wat je dan nog moet integreren over het interval [0, π/2] met θ als variabele om deze uitkomst te verkrijgen.
[ Bericht 0% gewijzigd door Riparius op 17-05-2011 06:40:01 ]


Persoonlijk vind ik dat je nogal moeilijk doet om de integratiegrenzen voor r te bepalen. Uit de voorwaarde x+y <= 1 is al meteen op te maken dat je voor als ondergrens voor r kunt kiezen voorquote:Op dinsdag 17 mei 2011 06:31 schreef Riparius het volgende:
[..]
Ik zal je toch maar even op weg helpen, want ik denk dat je de berekening hiervan een beetje onderschat. Ook zie ik dat je steeds probeert om bij het gebied waarover je wil integreren vaste onder- en bovengrenzen te bepalen voor je beide integratievariabelen terwijl dat in zijn algemeenheid niet gaat, ook hier niet.
Laten we eerst eens kijken hoe je de integraal van
(1) f(x,y) = 1/(x2+y2)2
over het gebied
(2) D := {(x;y) ∈ R2 | x2 + y2 ≤ 1 ∧ x + y ≥ 1}
kunt opschrijven in cartesische co÷rdinaten, dus zonder transformatie naar poolco÷rdinaten.
Het gebied D is een cirkelsegment dat, uitgezonderd de beide randpunten (1;0) en (0;1), geheel in het eerste kwadrant ligt en dat wordt begrensd door het deel van de eenheidscirkel dat zich in het eerste kwadrant bevindt en het lijnstuk dat de beide punten (1;0) en (0;1) verbindt.
Als we nu variabele x het interval [0,1] laten doorlopen, dan behoort daarbij voor elke waarde van x uit dit interval een interval voor y waarvan de ondergrens wordt bepaald door de lijn met vergelijking x + y = 1 en de bovengrens door de cirkel met vergelijking x2 + y2 = 1. Aangezien D in het eerste kwadrant ligt geldt hierbij in ieder geval y ≥ 0. Uit x + y = 1 volgt:
(3) y = 1 - x
En uit x2 + y2 = 1 volgt in combinatie met y ≥ 0:
(4) y = √(1 - x2)
Voor elke x zodanig dat 0 ≤ x ≤ 1 is dus 1 - x ≤ y ≤ √(1 - x2), en dus kunnen we het gebied D ook als volgt definiŰren:
(5) D := {(x;y) ∈ R2 | 0 ≤ x ≤ 1 ∧ 1 - x ≤ y ≤ √(1 - x2)}
Kijk voor een plaatje even hier.
De clou is natuurlijk dat we nu de integraal van f(x,y) over D (dankzij het theorema van Fubini) kunnen schrijven als een herhaalde integraal, als volgt:
[ afbeelding ]
Ik zou je niet aanraden deze integraal met de hand uit te rekenen. We kunnen de berekening beter hanteerbaar maken door over te gaan op poolco÷rdinaten. Om dit te kunnen doen moeten we eerst het gebied D definiŰren in poolco÷rdinaten, maar dan wel zˇ dat we de integraal van f(x,y) over D weer kunnen schrijven als een herhaalde integraal.
Aangezien het gebied D, uitgezonderd de punten met co÷rdinaten (1;0) en (0;1), geheel in het eerste kwadrant ligt, weten we al dat bij gebruik van poolco÷rdinaten geldt:
(6) 0 ≤ θ ≤ π/2
Maar nu moeten we voor elke waarde van θ op het interval [0, π/2] een onder- en een bovengrens voor r bepalen. Voor de beide punten (1;0) en (0;1) op de rand van D die corresponderen met resp. θ = 0 en θ = π/2 is dit gemakkelijk: hier geldt r = 1, zodat we kunnen zeggen dat de onder- en bovengrens van r hier zijn samengevallen. Maar voor de andere waarden van θ en dus op het open interval (0, π/2) geldt dit niet.
Nemen we bijvoorbeeld θ = π/4, dus precies halverwege het interval [0, π/2], dan zitten we op een lijn die een hoek maakt van 45 graden met de positieve x-as. Dit is uiteraard de lijn met vergelijking x = y, voor zover deze in het eerste kwadrant ligt. Deze lijn snijdt de lijn met vergelijking x + y = 1 in het punt met co÷rdinaten (½;½) en de eenheidscirkel in het punt met co÷rdinaten (½√2;½√2). Het interval waarover r moet lopen voor θ = π/4 wordt nu bepaald door de afstanden tot de oorsprong van deze twee snijpunten.
De bovengrens is eenvoudig, want voor elk punt op de eenheidscirkel is immers r = 1. De bovengrens van het interval waarover r moet lopen voor een gegeven waarde van θ op het interval [0, π/2] ligt dus vast. Maar voor de ondergrens geldt dat niet: de afstand van de oorsprong tot een punt op het lijnstuk dat de punten (0;1) en (0;1) verbindt is variabel en afhankelijk van θ. In het speciale geval θ = π/4 dat we nu bekijken is de afstand van het snijpunt (½;½) tot de oorsprong gelijk aan ½√2, zodat we kunnen concluderen dat voor θ = π/4 geldt ½√2 ≤ r ≤ 1.
Maar dit is niet voldoende: we moeten voor elke waarde van θ op het open interval (0, π/2) de ondergrens van het interval waarover r moet lopen bepalen, in functie van θ. Anders gezegd, we moeten voor elk punt P op het lijnstuk dat de punten met co÷rdinaten (1;0) en (0;1) verbindt de afstand OP = r tot de oorsprong bepalen als functie van de hoek θ die OP maakt met de positieve x-as. Dit betekent niets anders dan dat we een vergelijking in poolco÷rdinaten moeten opstellen van de lijn met de cartesische vergelijking x + y = 1.
Laten we het punt met de co÷rdinaten (1;0) punt A noemen, en zij P een willekeurig punt (anders dan A) op het lijnstuk van A naar het punt (0;1). In driehoek OAP hebben we nu:
(7) ∠AOP = θ en ∠PAO = π/4
En aangezien de som van de hoeken van een driehoek π (radialen) bedraagt, hebben we dus ook:
(8) ∠OPA = π - (π/4 + θ) = ¾π - θ
Volgens de sinusregel hebben we nu in driehoek OAP:
(9) OP : sin ∠PAO = OA : sin ∠OPA
En aangezien OP = r en OA =1 volgt met (7) en (8) dus uit (9) dat:
(10) r : sin(π/4) = 1 : sin(¾π - θ)
En aangezien sin(π/4) = ½√2 hebben we dus:
(11) r = √2/(2∙sin(¾π - θ))
Dit is dus een vergelijking in poolco÷rdinaten van de lijn waarvan de vergelijking in cartesische co÷rdinaten x + y = 1 luidt. Je kunt gemakkelijk nagaan dat voor θ = 0 en θ = π/2 geldt r = 1, terwijl voor θ = π/4 geldt r = ½√2, in overeenstemming met wat we eerder hadden gevonden. Voor het gebied D hebben we nu in poolco÷rdinaten:
(12) 0 ≤ θ ≤ π/2, √2/(2∙sin(¾π - θ)) ≤ r ≤ 1
Nu kunnen we de integraal van f(x,y) = 1/(x2 + y2)2 over D transformeren in een herhaalde integraal in poolco÷rdinaten. We hebben x2 + y2 = r2 en dus 1/(x2 + y2)2 = 1/r4. Bij een variabele substitutie van een integraal in meerdere variabelen moeten we ook nog rekening houden met de determinant van de Jacobiaan, die de schaalfactor geeft voor de transformatie. Bij een transformatie van cartesische co÷rdinaten naar poolco÷rdinaten is dit eenvoudig r, zodat dxdy = dydx vervangen wordt door rdrdθ. We krijgen dan:
[ afbeelding ]
Zoals verwacht, is de uitkomst 1/2. Probeer nu zelf deze integraal wel met de hand uit te werken. Als je het goed doet vind je na integratie met r als variabele en na wat goniometrische herleidingen voor de binnenste integraal sin θ∙cos θ, wat je dan nog moet integreren over het interval [0, π/2] met θ als variabele om deze uitkomst te verkrijgen.
1/(cosθ + sin θ)


Hier was ik weer. 
Ik heb er nu eentje waar ik dus echt niet uitkom: tan2 x = sin x. Zodra ik tan2 wil vervangen met behulp van sin/cos=tan (met de kwadratering erin) loop ik vast en andersom (sin x vervangen met cos x keer tan x) ook. Wie kan mij vertellen hoe ik dit op moet lossen? Ik kan er helaas bar weinig over vinden op internet (en in mij boek staat ook niet echt een toelichting). Met vastlopen bedoel ik dat ik er met ontbinden en de ABC-formule niet uitkom, enzovoorts.
Ik heb er nu eentje waar ik dus echt niet uitkom: tan2 x = sin x. Zodra ik tan2 wil vervangen met behulp van sin/cos=tan (met de kwadratering erin) loop ik vast en andersom (sin x vervangen met cos x keer tan x) ook. Wie kan mij vertellen hoe ik dit op moet lossen? Ik kan er helaas bar weinig over vinden op internet (en in mij boek staat ook niet echt een toelichting). Met vastlopen bedoel ik dat ik er met ontbinden en de ABC-formule niet uitkom, enzovoorts.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Je hebt volkomen gelijk. Ik doe dit soort dingen te weinig.quote:Op dinsdag 17 mei 2011 07:54 schreef Don_Vanelli het volgende:
[..]
Persoonlijk vind ik dat je nogal moeilijk doet om de integratiegrenzen voor r te bepalen. Uit de voorwaarde x+y <= 1 is al meteen op te maken dat je voor als ondergrens voor r kunt kiezen voor
1/(cosθ + sin θ)
Uit x + y = 1, x = r∙cos θ, y = r∙sin θ volgt direct r∙(cos θ + sin θ) = 1 en dus r = 1/(cos θ + sin θ).
En inderdaad krijgen we dan:
[ Bericht 9% gewijzigd door Riparius op 17-05-2011 09:09:34 ]


Wat dacht je van:quote:Op dinsdag 17 mei 2011 08:16 schreef Pipo1234 het volgende:
Hier was ik weer.
Ik heb er nu eentje waar ik dus echt niet uitkom: tan2 x = sin x. Zodra ik tan2 wil vervangen met behulp van sin/cos=tan (met de kwadratering erin) loop ik vast en andersom (sin x vervangen met cos x keer tan x) ook. Wie kan mij vertellen hoe ik dit op moet lossen? Ik kan er helaas bar weinig over vinden op internet (en in mij boek staat ook niet echt een toelichting). Met vastlopen bedoel ik dat ik er met ontbinden en de ABC-formule niet uitkom, enzovoorts.
tan2x = sin2x / cos2x = sin2x / (1 - sin2x)
Dan krijgen we dus:
sin2x / (1 - sin2x) = sin x
En dus:
sin2x = sin x ∙(1 - sin2x)
Haakjes uitwerken:
sin2x = sin x - sin3x
Herleiden op nul:
sin3x + sin2x - sin x = 0
Factor sin x buiten haakjes halen:
sin x∙(sin2x + sin x - 1) = 0
Nu jij weer. Bedenk dat een product van twee factoren alleen nul kan zijn als (tenminste) ÚÚn van de factoren zelf nul is.


Het was mij vooral onduidelijk wßt ik nou wilde doen, wat ik wil weergeven. Gisteravond heb ik hier ook nog aan gezeten en de moeilijkheid voor mij zit in het weergeven van het gebied (in poolcoordinaten). Met deze uitleg is het (denk ik) een stuk duidelijker geworden, ik probeer het even in mijn eigen woorden weer te geven:quote:
Ik heb een functie in een gebied dat duidelijk niet rechthoekig is: Het is een deel van een cirkel dat afgesneden word door een rechte lijn (de schets van het gebied had ik goed).
Wat ik dus wil, is een ('redelijke') bijectie te geven van een simpeler gebied naar D.
Aangezien D een deel van een cirkel is en de uitdrukking x2+y2<=1 erin voorkomt, ligt het voor de hand om D in poolcoordinaten weer te geven.
Neem het gebied E, dat gevormd word door de r-as en de a-as.
Ik zoek een afbeelding g:(r,a)|-->(???, ??) zodat ik daarmee gebied D kan beschrijven.
Dus g:E-->D via een redelijke bijectie.
Aangezien D in poolcoordinaten word uitgedrukt, moet ik x/y uitdrukken in de hoek en de straal.
Dus x=rcos(a) en y=rsin(a). Aangezien ik weet hoe de afbeelding eruit ziet, weet ik dat de hoek over het gebied [0,1/2Pi] gaat: Dit zijn de randvoorwaarden voor de hoek ( oftewel: a loopt van 0 naar 1/2Pi).
De randvoorwaarden voor r zijn moeilijker:
Voor de bovengrens zie ik dat de punten worden weergegeven door een cirkel: r is dus constant. Om precies te zijn word de cirkel weergegeven door x2+y2=1, duidelijk is dat r=1 deze lijn beschrijft (het gaat ook met invullen zoals ik in de volgende stap doe).
Voor de ondergrens geldt: x+y>=1, dus x+y=1. Invullen van x=rcos(a) en y=rsin(a) geeft
r= 1/ (cos(a)+sin(a)).
Nu weet ik dus het gebied en kan ik in de oorspronkelijke formule x en y substitueren door respectievelijk rcos(a) en rsin(a) met gebied E als een rechtoek: [0,1/2Pi] x [1/(sin(a)+cos(a)),1] waardoor ik dus de theorema van Fubini kan gebruiken om te integreren.
Edit: Ik kom alleen niet uit met de integraal.
Ik krijg dus de functie 1/r^3, dat word -1/2 r^(-2). Randvoorwaarde van r invullen geeft dan:
1/2((cos(a)+sin(a))^3 -1)
Maar als ik die opsplits blijf ik met de integraal van -1/2a zitten, waar dus een getal met Pi uitkomt. Hoe moet ik dan op een half uitkomen?
[ Bericht 6% gewijzigd door Siddartha op 17-05-2011 14:29:07 ]


Dit gaat niet goed. We moeten eerst r-3 primitiveren naar r. Zoals je correct opmerkt is een primitieve hiervan:quote:Op dinsdag 17 mei 2011 12:03 schreef Siddartha het volgende:
[..]
Edit: Ik kom alleen niet uit met de integraal.
Ik krijg dus de functie 1/r^3, dat wordt -1/2 r^(-2). Randvoorwaarde van r invullen geeft dan:
1/2((cos(a)+sin(a))^3 -1)
Maar als ik die opsplits blijf ik met de integraal van -1/2a zitten, waar dus een getal met Pi uitkomt. Hoe moet ik dan op een half uitkomen?
(1) -½∙r-2
Het interval waarover we integreren is [1/(cos θ + sin θ), 1].
Dus krijgen we:
(2) [-½∙r-2]1/(cos θ + sin θ)1 = -½ + ½∙(cos θ + sin θ)2
Nu is:
(3) (cos θ + sin θ)2 = cos2θ + 2∙cosθ∙sin θ + sin2θ = 1 + 2∙cosθ∙sin θ
En dus hebben we voor (2):
(4) -½ + ½ + ½∙2∙cosθ∙sin θ = cosθ∙sin θ
Nu moeten we cosθ∙sin θ weer integreren met als variabele θ over het interval [0, π/2]. Om cosθ∙sin θ te primitiveren maken we gebruik van de identiteit:
(5) sin 2θ = 2∙cosθ∙sin θ
Zodoende is cosθ∙sin θ = ½∙sin 2θ, en een primitieve hiervan is -¼∙cos 2θ. Dus krijgen we uiteindelijk:
(6) [-¼∙cos 2θ]0π/2 = (-¼∙-1) - (-¼∙1) = ¼ + ¼ = ½.
That's all.
[ Bericht 0% gewijzigd door Riparius op 17-05-2011 16:45:37 ]


Ah, om de een of andere reden herleide ik wel de integraal tot -1/2r-2, maar ging ik daarna meteen weer verder met -1/2r-3 als integraal. Een stom foutje, denk ik.quote:Op dinsdag 17 mei 2011 16:08 schreef Riparius het volgende:
[..]
Dit gaat niet goed. We moeten eerst r-3 primitiveren naar r. Zoals je correct opmerkt is een primitieve hiervan:
(1) -½∙r-2
Heel erg bedankt voor de uitgebreide uitleg (en het geduld)!



