Van de week was er zo'n collega die kwam met een soort van raadsel die op het eerste gezicht vrij simpel lijkt maar volgens mij toch bijna onmogelijk is 
Ik heb hem ff snel uitgetekend
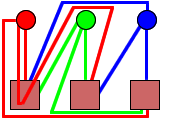
Er staan dus 3 huizen, en die hebben alle drie Gas, Water en Elektriciteit nodig.
Nu moet je die 3 dus aansluiten op alle huizen, maar de lijnen mogen elkaar niet kruizen of onderbreken.
Ik kom altijd vast te zitten bij die laatste lijn
Ik heb hem ff snel uitgetekend
Er staan dus 3 huizen, en die hebben alle drie Gas, Water en Elektriciteit nodig.
Nu moet je die 3 dus aansluiten op alle huizen, maar de lijnen mogen elkaar niet kruizen of onderbreken.
Ik kom altijd vast te zitten bij die laatste lijn
One hundred percent independent, I'm the fucking boss


Je moet van deur wisselen, dat verdubbelt je kans.
❤ Rozen zijn rood ❤
❤ Viooltjes zijn blauw ❤
❤ Kristel, ik hou van jou! ❤
❤ Viooltjes zijn blauw ❤
❤ Kristel, ik hou van jou! ❤


Die derde lijn moet dan ook ondergronds.
Op woensdag 22 mei 2013 21:42 schreef Dr_Flash het volgende:
Ik moet er ook idd niet zo over zaniken. Sorry :P
Ik moet er ook idd niet zo over zaniken. Sorry :P


Het kan ook niet 
Bio is baas. Ik ben niet meer op straat. Ik rij alleen langs om te kijken hoe het gaat.


2 gaatjes in het papier maken. en daar je lijn doorheen laten gaan. 
Gonna live while I'm alive, I'll sleep when I'm dead!


Ik ben nu 26 en probeer dit al op te lossen sinds m'n 10de levensjaar. Het is me nog steeds niet gelukt 
batman!


Hij zegt dat het moet kunnen, heeft me 20 euro beloofd als ik met de oplossing kwam 
One hundred percent independent, I'm the fucking boss


In het echt liggen ze allemaal ondergrondsquote:Op dinsdag 8 december 2009 18:43 schreef Fha het volgende:
Die derde lijn moet dan ook ondergronds.
Free Assange! Hack the Planet
[b]Op dinsdag 6 januari 2009 19:59 schreef Papierversnipperaar het volgende:[/b]
De gevolgen van de argumenten van de anti-rook maffia
[b]Op dinsdag 6 januari 2009 19:59 schreef Papierversnipperaar het volgende:[/b]
De gevolgen van de argumenten van de anti-rook maffia


onder het huisje door 
Op donderdag 22 mei 2008 10:28 schreef Spittie het volgende:
swarma spam hoer
Op maandag 4 mei 2009 16:09 schreef Broekpaling het volgende:
Swarmahoer, deleting your posts while users are still writing them.
Op maandag 4 mei 2009 16:09 schreef Broekpaling het volgende:
Swarmahoer, deleting your posts while users are still writing them.


Je kunt ook een huis voorzien van zonnepanelen
❤ Rozen zijn rood ❤
❤ Viooltjes zijn blauw ❤
❤ Kristel, ik hou van jou! ❤
❤ Viooltjes zijn blauw ❤
❤ Kristel, ik hou van jou! ❤


Je moet een dimensie toevoegen 
"De wetende is karig met zijn woorden; de woordenrijke is onwetend."
Lao-Tse
PSN(ps3): Appelknaller
Lao-Tse
PSN(ps3): Appelknaller


Nietusquote:Op dinsdag 8 december 2009 18:45 schreef Papierversnipperaar het volgende:
[..]
In het echt liggen ze allemaal ondergronds
Op woensdag 22 mei 2013 21:42 schreef Dr_Flash het volgende:
Ik moet er ook idd niet zo over zaniken. Sorry :P
Ik moet er ook idd niet zo over zaniken. Sorry :P


Mij is het gelukt anders
Op zaterdag 12 juli 2014 20:53 schreef Misstique het volgende:
Ik zou je nog niet uitnodigen voor m'n crematie.
Op maandag 22 juli 2013 21:18 schreef capuchon_jongen het volgende:
Sowieso je hebt me topic verneukt stevenmac :r
Ik zou je nog niet uitnodigen voor m'n crematie.
Op maandag 22 juli 2013 21:18 schreef capuchon_jongen het volgende:
Sowieso je hebt me topic verneukt stevenmac :r


haha die zou opzich wel kunnen, volgens mij is dat ook gewoon de oplossingquote:Op dinsdag 8 december 2009 18:44 schreef switchboy het volgende:
2 gaatjes in het papier maken. en daar je lijn doorheen laten gaan.
One hundred percent independent, I'm the fucking boss


Zo moeilijk is het anders nietquote:
Laatste lijntje laat je de andere kant op gaan voordat je het laatste blauwe lijntje maakt
Op zaterdag 12 juli 2014 20:53 schreef Misstique het volgende:
Ik zou je nog niet uitnodigen voor m'n crematie.
Op maandag 22 juli 2013 21:18 schreef capuchon_jongen het volgende:
Sowieso je hebt me topic verneukt stevenmac :r
Ik zou je nog niet uitnodigen voor m'n crematie.
Op maandag 22 juli 2013 21:18 schreef capuchon_jongen het volgende:
Sowieso je hebt me topic verneukt stevenmac :r


er staat nergens dat het 3 aparte lijnen moeten zijn. Dus lekker doorlussen
opgelost, slotje
maoam is voor bazen!


Is volgens mij een keer met de computer geprobeerd en toen was er geen oplossing.
The Pope? How many divisions has he got?


Ja dat mag dus nietquote:Op dinsdag 8 december 2009 18:53 schreef renedis het volgende:
[ afbeelding ]
er staat nergens dat het 3 aparte lijnen moeten zijn. Dus lekker doorlussen
opgelost, slotje
One hundred percent independent, I'm the fucking boss


Je kan de lijn door een huisje tekenen 


Want ik ben verzekerd, dat noch dood noch leven, noch engelen noch machten, noch heden noch toekomst, noch krachten, noch hoogte noch diepte, noch iets anders mij zal kunnen scheiden van de liefde van God.


komt ie nu mee.. ik helemaal jou karige paint aangepast, mag het opeens niet.quote:
Slechte OP hoor
maoam is voor bazen!


niet de elektriciteitskabel dan. Straks woont er iemand met een wietplantage.quote:Op dinsdag 8 december 2009 18:54 schreef Hetiszover het volgende:
Je kan de lijn door een huisje tekenen

Football. Glorious football. Dont care what it looks like.


haquote:Op dinsdag 8 december 2009 18:56 schreef renedis het volgende:
probeer eerst dit lijntje:
[ afbeelding ]
misschien dat je er dan uit komt.
ha
ha
The Pope? How many divisions has he got?


kunnen niet worden opgelost met de computer?quote:Op dinsdag 8 december 2009 18:53 schreef J.Stalin het volgende:
Is volgens mij een keer met de computer geprobeerd en toen was er geen oplossing.
[ Bericht 29% gewijzigd door vernargta op 09-12-2009 09:50:15 ]


quote:Op dinsdag 8 december 2009 18:56 schreef renedis het volgende:
probeer eerst dit lijntje:
[ afbeelding ]
misschien dat je er dan uit komt.


Er is geen 2-dimensionale oplossing. Wat wel kan: neem een donut met grote straal R en kleine straal r, dan wordt het oppervlak gegeven door
x= (R + r*cos(f))*cos( g)
y= (R + r*cos(f))*sin( g)
z= r*sin(f)
zodat elk punt op een torus met stralen R en r gegeven wordt door een (f,g) --> 2 coordinaten, dus 2D(boloppervlak hetzelfde )
Voor een mobiusrin hetzelfde verhaal voor de 2D heid ervan...ik heb het ding nu ook eens uitgekinpt en getekend om de discussie hier te volgen, conclusies :
1) als je een niet nul dikte aanneemt(ie de "boven" en "onderkant" zijn verschillende punten, dan lukt het niet, die blauwe en groene lijn gaan niet van positie wisselen zoals op de figuur online
2) ga je ervan uit dat het ding een dikte nul heeft en dus de "boven" en "onder"kant dezelfde punten zijn dan lukt hebt wel, dan komt de laatste gas en water aansluiting voor het derde beide aande "onder"kant aan, de ene van links en de ander van rechts.
(gewoon es proberen)
x= (R + r*cos(f))*cos( g)
y= (R + r*cos(f))*sin( g)
z= r*sin(f)
zodat elk punt op een torus met stralen R en r gegeven wordt door een (f,g) --> 2 coordinaten, dus 2D(boloppervlak hetzelfde )
Voor een mobiusrin hetzelfde verhaal voor de 2D heid ervan...ik heb het ding nu ook eens uitgekinpt en getekend om de discussie hier te volgen, conclusies :
1) als je een niet nul dikte aanneemt(ie de "boven" en "onderkant" zijn verschillende punten, dan lukt het niet, die blauwe en groene lijn gaan niet van positie wisselen zoals op de figuur online
2) ga je ervan uit dat het ding een dikte nul heeft en dus de "boven" en "onder"kant dezelfde punten zijn dan lukt hebt wel, dan komt de laatste gas en water aansluiting voor het derde beide aande "onder"kant aan, de ene van links en de ander van rechts.
(gewoon es proberen)
Want ik ben verzekerd, dat noch dood noch leven, noch engelen noch machten, noch heden noch toekomst, noch krachten, noch hoogte noch diepte, noch iets anders mij zal kunnen scheiden van de liefde van God.


quote:Op dinsdag 8 december 2009 19:01 schreef Hetiszover het volgende:
Er is geen 2-dimensionale oplossing. Wat wel kan: neem een donut met grote straal R en kleine straal r, dan wordt het oppervlak gegeven door
x= (R + r*cos(f))*cos( g)
y= (R + r*cos(f))*sin( g)
z= r*sin(f)
zodat elk punt op een torus met stralen R en r gegeven wordt door een (f,g) --> 2 coordinaten, dus 2D(boloppervlak hetzelfde )
Voor een mobiusrin hetzelfde verhaal voor de 2D heid ervan...ik heb het ding nu ook eens uitgekinpt en getekend om de discussie hier te volgen, conclusies :
1) als je een niet nul dikte aanneemt(ie de "boven" en "onderkant" zijn verschillende punten, dan lukt het niet, die blauwe en groene lijn gaan niet van positie wisselen zoals op de figuur online
2) ga je ervan uit dat het ding een dikte nul heeft en dus de "boven" en "onder"kant dezelfde punten zijn dan lukt hebt wel, dan komt de laatste gas en water aansluiting voor het derde beide aande "onder"kant aan, de ene van links en de ander van rechts.
(gewoon es proberen)
[ afbeelding ]


Ik snap er niks van  alleen dat je het blijkbaar moet vouwen ofzo
alleen dat je het blijkbaar moet vouwen ofzo
One hundred percent independent, I'm the fucking boss


Wat een eye-opener.quote:Op dinsdag 8 december 2009 19:01 schreef Hetiszover het volgende:
Er is geen 2-dimensionale oplossing. Wat wel kan: neem een donut met grote straal R en kleine straal r, dan wordt het oppervlak gegeven door
x= (R + r*cos(f))*cos( g)
y= (R + r*cos(f))*sin( g)
z= r*sin(f)
zodat elk punt op een torus met stralen R en r gegeven wordt door een (f,g) --> 2 coordinaten, dus 2D(boloppervlak hetzelfde )
Voor een mobiusrin hetzelfde verhaal voor de 2D heid ervan...ik heb het ding nu ook eens uitgekinpt en getekend om de discussie hier te volgen, conclusies :
1) als je een niet nul dikte aanneemt(ie de "boven" en "onderkant" zijn verschillende punten, dan lukt het niet, die blauwe en groene lijn gaan niet van positie wisselen zoals op de figuur online
2) ga je ervan uit dat het ding een dikte nul heeft en dus de "boven" en "onder"kant dezelfde punten zijn dan lukt hebt wel, dan komt de laatste gas en water aansluiting voor het derde beide aande "onder"kant aan, de ene van links en de ander van rechts.
(gewoon es proberen)
[ afbeelding ]
[ Bericht 0% gewijzigd door o.us op 08-12-2009 19:04:59 ]
Feyenoord Rotterdam


Ja, en dat met mbo dierverzorging.quote:
Want ik ben verzekerd, dat noch dood noch leven, noch engelen noch machten, noch heden noch toekomst, noch krachten, noch hoogte noch diepte, noch iets anders mij zal kunnen scheiden van de liefde van God.


Jep! 
Niemand heeft gezegd dat je niet door de suppliers heen mag!
Niemand heeft gezegd dat je niet door de suppliers heen mag!
Prrrrttt
Op dinsdag 12 oktober 2010 19:11 schreef 4EverBlackEyed het volgende:Perry is de oppercavia :')
Op dinsdag 12 oktober 2010 19:11 schreef 4EverBlackEyed het volgende:Perry is de oppercavia :')


En ts verdient 20 euro die hij gaat delen met ons allemaal
Op zaterdag 12 juli 2014 20:53 schreef Misstique het volgende:
Ik zou je nog niet uitnodigen voor m'n crematie.
Op maandag 22 juli 2013 21:18 schreef capuchon_jongen het volgende:
Sowieso je hebt me topic verneukt stevenmac :r
Ik zou je nog niet uitnodigen voor m'n crematie.
Op maandag 22 juli 2013 21:18 schreef capuchon_jongen het volgende:
Sowieso je hebt me topic verneukt stevenmac :r


Tja, de vraag is of die vent het wel goed keurtquote:Op dinsdag 8 december 2009 19:17 schreef stevenmac26 het volgende:
En ts verdient 20 euro die hij gaat delen met ons allemaal
One hundred percent independent, I'm the fucking boss


Waarom zou hij het niet goedkeuren??? Zo win je nooitquote:Op dinsdag 8 december 2009 19:18 schreef J.Herrer het volgende:
[..]
Tja, de vraag is of die vent het wel goed keurt
Op zaterdag 12 juli 2014 20:53 schreef Misstique het volgende:
Ik zou je nog niet uitnodigen voor m'n crematie.
Op maandag 22 juli 2013 21:18 schreef capuchon_jongen het volgende:
Sowieso je hebt me topic verneukt stevenmac :r
Ik zou je nog niet uitnodigen voor m'n crematie.
Op maandag 22 juli 2013 21:18 schreef capuchon_jongen het volgende:
Sowieso je hebt me topic verneukt stevenmac :r


begin anders eerst effe met een wat makkelijkere puzzel.
pen op papier, 4 rechte lijnen (aan elkaar dus), en dan pen van papier af.
door elk punt moet je pen 1 keer gaan.
|
|