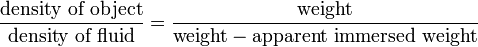SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Ohnee 
Op vrijdag 11 september 2009 18:32 schreef jogy het volgende:
Ik ben zo trots op je dat ik je in brons wil gieten, in de achtertuin wil zetten met een tuinslang door je mond als appelsjapfontein.
Ik ben zo trots op je dat ik je in brons wil gieten, in de achtertuin wil zetten met een tuinslang door je mond als appelsjapfontein.
Eigenlijk is het heel simpel: de prefix voor de eenheid geeft de vermenigvuldigingsfactor (in machten van 10) aan.
vergelijk:
1 mM/L is dus 1 millimol per liter is dus 1/1000 mol per liter,
1 MM/L is dus 1 megamol per liter is dus 1000000 mol per liter.
vergelijk:
1 mM/L is dus 1 millimol per liter is dus 1/1000 mol per liter,
1 MM/L is dus 1 megamol per liter is dus 1000000 mol per liter.
alleen staat de M voor mol/L, dus het is wel mmol/L en Mmol/Lquote:Op zaterdag 5 september 2009 18:09 schreef ErictheSwift het volgende:
Eigenlijk is het heel simpel: de prefix voor de eenheid geeft de vermenigvuldigingsfactor (in machten van 10) aan.
vergelijk:
1 mM/L is dus 1 millimol per liter is dus 1/1000 mol per liter,
1 MM/L is dus 1 megamol per liter is dus 1000000 mol per liter.
You don't have to know why you do something to stop doing it. All you have to do is to take a close look at what you are actually doing and decide to stop doing it for that moment!"
Student chemie reporting in, zal proberen ook wat mee te beantwoorden!
Een handige kleine opmerking hierbij is trouwens dat mmol/ml gelijk is aan mol/l. Handig bij titraties (als je 't daarom vroeg
).
Nu zit ik zelf met een vraag rond mechanica, beetje een struikelblok voor mij helaas...
Als jullie mij op weg zetten is 't ook goed hoor
.
'T gaat als volgt:
Bereken de minimumsnelheid v(0) waarmee een stuntrijder een helling van 15° moet verlaten om over de sloot te geraken. De helling is 2 meter hoog, de sloot eindigt op 3 meter van het einde van de helling.
De oplossing is 4,1 m/s maar ik kan de parabool echt niet zelf berekenen... Voor elk formuletje dat ik kan bedenken kom ik een gegeven te kort
.
Alvast thx!
[ Bericht 6% gewijzigd door tony_clifton- op 07-09-2009 22:06:50 ]
Klopt in dit geval, maar niet alle zouten zijn goed oplosbaar! Zouten van zwakke zuren zijn bijvoorbeeld vaak weinig tot slecht oplosbaar. Aan de andere kant zijn er ook slecht oplosbare zouten van sterke zuren (bv. AgCl met een Ksp van 2x10^-10).quote:Op donderdag 3 september 2009 15:37 schreef Slotje9000 het volgende:
[..]
Oh, ik heb het al
Het was dat aluminiumbromide een zout is, dus moet je de ionen nemen
quote:Op zaterdag 5 september 2009 18:31 schreef teigan het volgende:
[..]
alleen staat de M voor mol/L, dus het is wel mmol/L en Mmol/L
Een handige kleine opmerking hierbij is trouwens dat mmol/ml gelijk is aan mol/l. Handig bij titraties (als je 't daarom vroeg
).Nu zit ik zelf met een vraag rond mechanica, beetje een struikelblok voor mij helaas...
Als jullie mij op weg zetten is 't ook goed hoor
.'T gaat als volgt:
Bereken de minimumsnelheid v(0) waarmee een stuntrijder een helling van 15° moet verlaten om over de sloot te geraken. De helling is 2 meter hoog, de sloot eindigt op 3 meter van het einde van de helling.
De oplossing is 4,1 m/s maar ik kan de parabool echt niet zelf berekenen... Voor elk formuletje dat ik kan bedenken kom ik een gegeven te kort
.Alvast thx!
[ Bericht 6% gewijzigd door tony_clifton- op 07-09-2009 22:06:50 ]
Ik zou het zo doen:
De stuntrijder valt met een versnelling van 9.8m/s2, dus hij moet genoeg voorwaartse snelheid hebben om dat te compenseren. Zeg dat hij met snelheid v van de helling komt. De hoek is 15°, dus je kunt de componenten uitrekenen, de verticale component is is sin(15)·v en de horizontale is cos(15)·v.
Zijn verticaal afgelegde afstand is (neem de helling als 2):
2 + sin(15)·v + 1/2at2, waarbij a negatief is.
Zijn horizontaal afgelegde afstand is:
0 + cos(15)·v·t
We willen dat hier 3 uitkomt, anders haalt hij het niet, dus daaruit berekenen we dat:
Dat kun je nu invullen in de vergelijking voor zijn verticale beweging:
En we willen dat hier (minstens) 0 uitkomt, dus stel dat gelijk, en stop dat in een oplosser, en er komt zoiets uit.
Maar ik kom dan op 3.95m/s, niet 4.1.
De stuntrijder valt met een versnelling van 9.8m/s2, dus hij moet genoeg voorwaartse snelheid hebben om dat te compenseren. Zeg dat hij met snelheid v van de helling komt. De hoek is 15°, dus je kunt de componenten uitrekenen, de verticale component is is sin(15)·v en de horizontale is cos(15)·v.
Zijn verticaal afgelegde afstand is (neem de helling als 2):
2 + sin(15)·v + 1/2at2, waarbij a negatief is.
Zijn horizontaal afgelegde afstand is:
0 + cos(15)·v·t
We willen dat hier 3 uitkomt, anders haalt hij het niet, dus daaruit berekenen we dat:
Dat kun je nu invullen in de vergelijking voor zijn verticale beweging:
En we willen dat hier (minstens) 0 uitkomt, dus stel dat gelijk, en stop dat in een oplosser, en er komt zoiets uit.
Maar ik kom dan op 3.95m/s, niet 4.1.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Heeft te maken met radialen vs gradenquote:Op maandag 7 september 2009 22:14 schreef Iblis het volgende:
Maar ik kom dan op 3.95m/s, niet 4.1.
Hij was maar een clown...
Die solver gebruikt gewoon graden hoor.quote:
[..]
Heeft te maken met radialen vs graden
[edit]
Hmm, ik zie wat je bedoelt, als je ‘radians’ aanklikt dan kom je inderdaad op 4,1 (of 4,05) uit. Dat zou wat verklaren, maar dat betekent dat de voorbeeldoplossing fout is.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Door ziekte een les gemist, hoop dat iemand me hiermee kan helpen
(Alles tussen haakjes moeten coördinaatvoorstellingen van vectoren voorstellen)
m = (-1, 0, 2) + a*(5, -2, 0)
W = b(2, -1, 1) + c(1, 3 ,-1)
Bereken de vector r van het snijpunt R van m met het vlak W
Nu had ik bedacht dat ik deze twee vergelijkingen gelijk aan elkaar moest stellen, om ze daarna op te lossen met eliminatie&substitutie etc.
Nu kreeg ik hieruit uiteindelijk het antwoord
r = (8, -4, 2)
Dan de misschien heel domme vraag, in de antwoorden staat r = (4, -2, 1), is dit hetzelfde als mijn antwoord of heb ik toch ergens iets fout gedaan?
Alvast bedankt
(Alles tussen haakjes moeten coördinaatvoorstellingen van vectoren voorstellen)
m = (-1, 0, 2) + a*(5, -2, 0)
W = b(2, -1, 1) + c(1, 3 ,-1)
Bereken de vector r van het snijpunt R van m met het vlak W
Nu had ik bedacht dat ik deze twee vergelijkingen gelijk aan elkaar moest stellen, om ze daarna op te lossen met eliminatie&substitutie etc.
Nu kreeg ik hieruit uiteindelijk het antwoord
r = (8, -4, 2)
Dan de misschien heel domme vraag, in de antwoorden staat r = (4, -2, 1), is dit hetzelfde als mijn antwoord of heb ik toch ergens iets fout gedaan?
Alvast bedankt
Wat had jij voor a, b en c zodat het snijpunt (8, -4, 2) is?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
a=1, b=2 en c=0
oh, zie nu pas dat ie in het verkeerde topic staat
[ Bericht 67% gewijzigd door woopehh op 10-09-2009 21:13:32 ]
oh, zie nu pas dat ie in het verkeerde topic staat
[ Bericht 67% gewijzigd door woopehh op 10-09-2009 21:13:32 ]
Ik heb ruzie met de Wet van Archimedes. 
Het doel van het experiment is om de dichtheid van een object te bepalen. Het object werd in een beker met water gehangen en het verschil werd gewogen.
FA = ρ . g . V
ρ water = 0,99788 g/mL
g = 9,81 m/s2
Beker met vloeistof = 90,7 g
Beker met vloeistof met object = 96,9 g
Wat is de V in de formule? Welke gegevens heb je nog nodig om de dichtheid van het object te berekenen? Welke stappen moeten er genomen worden?
De dichtheid zal iets van 7 a 8 g/mL moeten zijn (dit hebben we al berekent met ρ=m/V van het object zelf).
Het doel van het experiment is om de dichtheid van een object te bepalen. Het object werd in een beker met water gehangen en het verschil werd gewogen.
FA = ρ . g . V
ρ water = 0,99788 g/mL
g = 9,81 m/s2
Beker met vloeistof = 90,7 g
Beker met vloeistof met object = 96,9 g
Wat is de V in de formule? Welke gegevens heb je nog nodig om de dichtheid van het object te berekenen? Welke stappen moeten er genomen worden?
De dichtheid zal iets van 7 a 8 g/mL moeten zijn (dit hebben we al berekent met ρ=m/V van het object zelf).
"Everything we are, we are when we're alone."
Je moet kijken hoeveel het water opzij is geduwd. Je hebt nu alleen maar gemeten dat het object 6,2g weegt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Hoe heb je dan een verschilweging gedaan? M.a.w. hoe had je dat object in het water, wat mat je precies? Want ik dacht ook dat je een bak water op een weegschaal had staan, daar het object in gooide, en toen het gewicht bepaalde.quote:
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
We hebben eerst het object zelf gewogen: 48,5 g.quote:Op vrijdag 11 september 2009 15:57 schreef Iblis het volgende:
[..]
Hoe heb je dan een verschilweging gedaan? M.a.w. hoe had je dat object in het water, wat mat je precies? Want ik dacht ook dat je een bak water op een weegschaal had staan, daar het object in gooide, en toen het gewicht bepaalde.
Daarna hebben we een beker met water gewogen op een weegschaal: 90,7 g
Daarna hebben we het object aan een touwtje ondergedompeld in de beker: 96,9 g
"Everything we are, we are when we're alone."
Je moet het object niet aan het touwtje omhoog tillen. De totale massa zou 90,7+48,5 gram moeten zijn.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Assuming Archimedes' principle to be reformulated as follows,
then inserted into the quotient
yields the formula below. The density of the immersed object relative to the density of the fluid can easily be calculated without measuring any volumes:
Wat betekent hier 'apparent immersed weight' en 'weight of displaced fluid'? Het gewone 'weight' is dan het gewicht van het object?
________________
Als ik bovenstaande formule invul:
ρ object / ρ water = gewicht object / gewicht verplaatste vloeistof
ρ object / .99788 = 48.5 / 6.2 geeft ρ object = 7,81 g/mL
Maar als dit klopt, dan snap ik niet waarom de formule FA = ρ . g . V gegeven is aangezien de g en V niet nodig zijn..
[ Bericht 23% gewijzigd door Meursault op 11-09-2009 16:43:38 ]
then inserted into the quotient
yields the formula below. The density of the immersed object relative to the density of the fluid can easily be calculated without measuring any volumes:
Wat betekent hier 'apparent immersed weight' en 'weight of displaced fluid'? Het gewone 'weight' is dan het gewicht van het object?
________________
Als ik bovenstaande formule invul:
ρ object / ρ water = gewicht object / gewicht verplaatste vloeistof
ρ object / .99788 = 48.5 / 6.2 geeft ρ object = 7,81 g/mL
Maar als dit klopt, dan snap ik niet waarom de formule FA = ρ . g . V gegeven is aangezien de g en V niet nodig zijn..
[ Bericht 23% gewijzigd door Meursault op 11-09-2009 16:43:38 ]
"Everything we are, we are when we're alone."
Maar dan meet je toch geen opwaartse kracht? Het idee is dat je een verschil ziet in gewicht en dat dat te maken heeft met de kracht die het water uitoefend op het object dat aan een touwtje hangt.quote:Op vrijdag 11 september 2009 16:07 schreef GlowMouse het volgende:
Je moet het object niet aan het touwtje omhoog tillen. De totale massa zou 90,7+48,5 gram moeten zijn.
"Everything we are, we are when we're alone."
In dat geval heb je als ‘apparent immersed weight’ 6,2g * g gemeten zou ik zeggen. Als het touwtje dus net niet slap hangt en net het object ook niet omhoog trekt. Maar dat is wel heel precair.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Kan iemand mij uitleggen wat een partieel afgeleide is. Kom er niet echt uit met de uitleg van Wikipedia.
Dit staat er in mijn sheets: wanneer we kijken naar oneindig kleine veranderingen, is MUy, de partiële afgeleide van U(x,y) naar y.
MUy = ∂U/∂Y
Hoe komen ze tot deze berekening? Doe nu zelf een premaster, heb zelf Havo en HBO gedaan, maar merk toch wel dat ik dit soort dingen ''mis''. Iemand tips hoe ik het oplossingen van vergelijkingen etc sneller op kan nemen?
Dit staat er in mijn sheets: wanneer we kijken naar oneindig kleine veranderingen, is MUy, de partiële afgeleide van U(x,y) naar y.
MUy = ∂U/∂Y
Hoe komen ze tot deze berekening? Doe nu zelf een premaster, heb zelf Havo en HBO gedaan, maar merk toch wel dat ik dit soort dingen ''mis''. Iemand tips hoe ik het oplossingen van vergelijkingen etc sneller op kan nemen?
Misschien dat deze in in [Bèta wiskunde] Huiswerk- en vragentopic beter op z’n plek is, maar je komt vaak partiële afgeleiden tegen bij natuurkunde, dus vooruit.quote:
Kan iemand mij uitleggen wat een partieel afgeleide is. Kom er niet echt uit met de uitleg van Wikipedia.
Dit staat er in mijn sheets: wanneer we kijken naar oneindig kleine veranderingen, is MUy, de partiële afgeleide van U(x,y) naar y.
MUy = ∂U/∂Y
Hoe komen ze tot deze berekening? Doe nu zelf een premaster, heb zelf Havo en HBO gedaan, maar merk toch wel dat ik dit soort dingen ''mis''. Iemand tips hoe ik het oplossingen van vergelijkingen etc sneller op kan nemen?
Zoals ook op de (Engelse) Wikipedia staat, als je een functie neemt met meer variabelen, bijvoorbeeld z = x2 + xy + y2:
Bron: Wikimedia Commons. Maker: Indeed123. Licentie: CC-BY-SA.
Dan zie je dat je concept van ‘raaklijn’ enigszins zinloos wordt. Je hebt in elk punt heel veel raaklijnen. Je kunt een raaklijn parallel aan de x-as tekenen, parallel aan de y-as, of welke richting dan ook op.
Meestal echter, omdat je de grafiek als functie van x en y beschouwt, ben je vooral geïnteresseerd hoe zo’n grafiek verandert als alleen x of y verandert. Neem je bijvoorbeeld y constant, bijvoorbeeld y = 1, dan krijg je deze doorsnede (er staat ook een raaklijn in als voorbeeld voor x = 1):
Bron: Wikimedia Commons. Maker: Indeed123. Licentie: CC-BY-SA.
Hiervan kun je weer eenduidig de raaklijn in een punt bepalen. De vergelijking van bovenstaande grafiek is (uiteraard) z = x2 + x + 1, wat je krijgt door y = 1 in te vullen in de eerdere formule.
Wat je dus in feite zegt in zo’n geval: Neem y constant. Goed, voor y = 2 krijg je een andere grafiek, en voor y = 4 weer een andere, maar in ieder geval is y constant. Dat idee neem je mee naar de partiële afgeleide. Dus als men schrijft:
, dan zegt men zoveel als ‘we bepalen de afgeleide van z naar x waarbij we doen alsof y een constante is. Je krijgt dus in feite hetzelfde als wanneer je f(x) = x2 + xy + y2 hebt en dat afleidt naar y, immers, voorgaande is alleen een functie in x. Zoiets kun je – als het goed is – allang afleiden, als je dat naar x afleidt, krijg je: 2x + y (immers, y2 is gewoon constant).
Neem nu weer: , dat wordt dus:
.
We kunnen ook het volgende bepalen:
.
Dan neem je dus x constant. In feite is dit dus alleen een notatie die zegt welke van de variabelen je als ‘variabel’ moet beschouwen, de rest moet je constant nemen. Je kunt ook twee keer afleiden:
.
Eerst neem je x constant, dan krijg je x + 2y, dan neem je y constant en leid je af naar x.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Hallo,
Ik heb 2 korte vraagjes over een flightsimulator:
1) Ik moet de hoek berekenen (van de simulator) waarbij de acceleratie 0,5g is.
2) Hoe groot is de maximale g-force die gesimuleerd kan worden?
Ik heb naar antwoorden gezocht maar kan eigenlijk niks over dit onderwerp vinden. Heeft iemand een idee en/of uitleg?
Alvast bedankt.
Ik heb 2 korte vraagjes over een flightsimulator:
1) Ik moet de hoek berekenen (van de simulator) waarbij de acceleratie 0,5g is.
2) Hoe groot is de maximale g-force die gesimuleerd kan worden?
Ik heb naar antwoorden gezocht maar kan eigenlijk niks over dit onderwerp vinden. Heeft iemand een idee en/of uitleg?
Alvast bedankt.
Alhoewel ik denk dat ik die vraag überhaupt niet kan beantwoorden denk ik dat er sowieso meer informatie nodig is. Wat voor simulator spreken we over?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Nee meer info was niet bijgevoegd. Het waren korte vraagjes, dus ik denk dat ik niet te moeilijk moet denken.quote:Op maandag 14 september 2009 13:03 schreef Iblis het volgende:
Alhoewel ik denk dat ik die vraag überhaupt niet kan beantwoorden denk ik dat er sowieso meer informatie nodig is. Wat voor simulator spreken we over?
Nou, dat lijkt me toch stug. De maximale G-kracht die gesimuleerd kan worden is namelijk voornamelijk afhankelijk van de specificaties van de simulator, en niet van de natuurwetten. Daarnaast is het werkingsprincipe van deze simulator onbekend, werkt het met veren, hydraulische zuigers, pneumatische zuigers of kabels? Zit je op een platform dat onder een hoek kan draaien? Of hang je aan kabels? Zomaar wat manieren die mij te binnen schieten die een simulator mogelijk zouden maken.
2000 light years from home
kan iemand mij helpen met dit probleem
Druk Fhandkracht uit in m.g van de emmer en de geometrie van de katrollen
hier het plaatje
http://img441.imageshack.us/i/natuurkunde3232.jpg/
Druk Fhandkracht uit in m.g van de emmer en de geometrie van de katrollen
hier het plaatje
http://img441.imageshack.us/i/natuurkunde3232.jpg/
Als ik met kracht F aan het touwtje trek, wat is dan de kracht omhoog in het touwtje dat aan katrol 2 hangt?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
ik wel
denk eens na
!
en kijk anders eens in het boek
denk eens na
!
en kijk anders eens in het boek
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
de opdrahct luidt:
2.13
Druk de handkracht Fhand uit in het gewicht van de emmer en de geometrie van de katrollen (Figuur 2.4).
met dat plaatje
we komen er niet uit met 6 1e jaar TU twenters-ers
help aub
2.13
Druk de handkracht Fhand uit in het gewicht van de emmer en de geometrie van de katrollen (Figuur 2.4).
met dat plaatje
we komen er niet uit met 6 1e jaar TU twenters-ers
help aub
Heb er nu pas serieus naar kunnen kijken maar nu begrijp ik het tnxquote:Op maandag 14 september 2009 11:37 schreef Iblis het volgende:
[..]
Misschien dat deze in in [Bèta wiskunde] Huiswerk- en vragentopic beter op z’n plek is, maar je komt vaak partiële afgeleiden tegen bij natuurkunde, dus vooruit.
Zoals ook op de (Engelse) Wikipedia staat, als je een functie neemt met meer variabelen, bijvoorbeeld z = x2 + xy + y2:
[ link | afbeelding ]
Bron: Wikimedia Commons. Maker: Indeed123. Licentie: CC-BY-SA.
Dan zie je dat je concept van ‘raaklijn’ enigszins zinloos wordt. Je hebt in elk punt heel veel raaklijnen. Je kunt een raaklijn parallel aan de x-as tekenen, parallel aan de y-as, of welke richting dan ook op.
Meestal echter, omdat je de grafiek als functie van x en y beschouwt, ben je vooral geïnteresseerd hoe zo’n grafiek verandert als alleen x of y verandert. Neem je bijvoorbeeld y constant, bijvoorbeeld y = 1, dan krijg je deze doorsnede (er staat ook een raaklijn in als voorbeeld voor x = 1):
[ link | afbeelding ]
Bron: Wikimedia Commons. Maker: Indeed123. Licentie: CC-BY-SA.
Hiervan kun je weer eenduidig de raaklijn in een punt bepalen. De vergelijking van bovenstaande grafiek is (uiteraard) z = x2 + x + 1, wat je krijgt door y = 1 in te vullen in de eerdere formule.
Wat je dus in feite zegt in zo’n geval: Neem y constant. Goed, voor y = 2 krijg je een andere grafiek, en voor y = 4 weer een andere, maar in ieder geval is y constant. Dat idee neem je mee naar de partiële afgeleide. Dus als men schrijft:
[ afbeelding ], dan zegt men zoveel als ‘we bepalen de afgeleide van z naar x waarbij we doen alsof y een constante is. Je krijgt dus in feite hetzelfde als wanneer je f(x) = x2 + xy + y2 hebt en dat afleidt naar y, immers, voorgaande is alleen een functie in x. Zoiets kun je – als het goed is – allang afleiden, als je dat naar x afleidt, krijg je: 2x + y (immers, y2 is gewoon constant).
Neem nu weer: [ afbeelding ], dat wordt dus:
[ afbeelding ].
We kunnen ook het volgende bepalen:
[ afbeelding ].
Dan neem je dus x constant. In feite is dit dus alleen een notatie die zegt welke van de variabelen je als ‘variabel’ moet beschouwen, de rest moet je constant nemen. Je kunt ook twee keer afleiden:
[ afbeelding ].
Eerst neem je x constant, dan krijg je x + 2y, dan neem je y constant en leid je af naar x.
ben je nu serieus?quote:
de opdrahct luidt:
2.13
Druk de handkracht Fhand uit in het gewicht van de emmer en de geometrie van de katrollen (Figuur 2.4).
met dat plaatje
we komen er niet uit met 6 1e jaar TU twenters-ers
help aub
Learn as if you're going to live forever, Live as if you're going to die tomorrow
De BIE®TAFELop youtube en dumpert _O_ >100k views *O*
I wanna die the same way I was born: Screaming and covered with blood
Arbeit macht frei. Ik heb nu 40 jaar vakantie *O*
De BIE®TAFELop youtube en dumpert _O_ >100k views *O*
I wanna die the same way I was born: Screaming and covered with blood
Arbeit macht frei. Ik heb nu 40 jaar vakantie *O*
Heel simpel maar ik kom er gewoon niet uit:
Je moet 1890 producten in 247.200 seconden maken.
Je kan of 80 seconden productietijd voor 1 product pakken of 160 seconden.
Met zoveel mogelijk producten in 160 seconden.
Hoeveel producten maak je in 80 seconden en hoeveel in 160?
Je moet 1890 producten in 247.200 seconden maken.
Je kan of 80 seconden productietijd voor 1 product pakken of 160 seconden.
Met zoveel mogelijk producten in 160 seconden.
Hoeveel producten maak je in 80 seconden en hoeveel in 160?
When I get sad, I stop being sad and just be awesome instead.
Je rekent eerst uit hoeveel producten je kan maken met 160 sec. per product met de totale tijd.quote:Op zondag 27 september 2009 14:44 schreef MouzurX het volgende:
Heel simpel maar ik kom er gewoon niet uit:
Je moet 1890 producten in 247.200 seconden maken.
Je kan of 80 seconden productietijd voor 1 product pakken of 160 seconden.
Met zoveel mogelijk producten in 160 seconden.
Hoeveel producten maak je in 80 seconden en hoeveel in 160?
247200 / 160 = 1545 producten
Je komt er dan 345 te kort. Je moet dus 345 keer 2 producten maken in de tijd dat je één producten zou maken om het totaal aantal producten binnen de tijd te halen.
Dus je maakt 1545 - 345 = 1200 producten met 160 sec. per product en de rest moet je 2x zo snel doen.
1890 - 1200 = 690
690 x 80 sec. per product
1200 x 160 + 690 x 80 = 247200 sec.
Beetje omslachtige uitleg misschien, maar is het helder?
"Everything we are, we are when we're alone."
x+y=1890
80x+160y=247200
en oplossen maar (mbv substitutie)
80x+160y=247200
en oplossen maar (mbv substitutie)
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Oke bedankt ik snap hemquote:Op zondag 27 september 2009 15:23 schreef Meursault het volgende:
[..]
Je rekent eerst uit hoeveel producten je kan maken met 160 sec. per product met de totale tijd.
247200 / 160 = 1545 producten
Je komt er dan 345 te kort. Je moet dus 345 keer 2 producten maken in de tijd dat je één producten zou maken om het totaal aantal producten binnen de tijd te halen.
Dus je maakt 1545 - 345 = 1200 producten met 160 sec. per product en de rest moet je 2x zo snel doen.
1890 - 1200 = 690
690 x 80 sec. per product
1200 x 160 + 690 x 80 = 247200 sec.
Beetje omslachtige uitleg misschien, maar is het helder?
When I get sad, I stop being sad and just be awesome instead.
Ja daar heb ik ook aan gedacht alleen ik snapte niet meer hoe ik dat substitutie moest doenquote:Op zondag 27 september 2009 15:26 schreef GlowMouse het volgende:
x+y=1890
80x+160y=247200
en oplossen maar (mbv substitutie)
When I get sad, I stop being sad and just be awesome instead.
x = 1890 - y
invullen in de tweede: 80(1890-y)+160y = 247200, en die heb je zo opgelost.
invullen in de tweede: 80(1890-y)+160y = 247200, en die heb je zo opgelost.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
151.200-80Y+160Y = 247.200quote:Op zondag 27 september 2009 15:33 schreef GlowMouse het volgende:
x = 1890 - y
invullen in de tweede: 80(1890-y)+160y = 247200, en die heb je zo opgelost.
80Y=96.000
Y = 1200
X = 1890-1200 = 690.
Oke, naja zover het nut van wiskunde B12(nog geen 2 jaar geleden en nu al vergeten
)
When I get sad, I stop being sad and just be awesome instead.
)
Crosspost vanuit het andere beta-huiswerktopic. Ik wist niet in welke hij thuishoorde!quote:Op zaterdag 3 oktober 2009 02:10 schreef Friek_ het volgende:
Hallo!
De voorbeeldtussentoets
Mijn antwoorden
