SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Vorige deel: [Bèta wiskunde] Huiswerk- en vragentopic
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
http://betahw.mine.nu/index.php: site van GlowMouse om formules te kunnen gebruiken in je posts (op basis van Latexcode wordt een plaatje gegenereerd dat je vervolgens via het aangegeven linkje kunt opnemen).
Een uitleg over LaTeX-code kun je hier vinden
Wiskundig inhoudelijk:
http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
OP
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
Een uitleg over LaTeX-code kun je hier vinden
Wiskundig inhoudelijk:
OP
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


Shit, gooi ik met die nutteloze post ook het topic nog dicht. In de herkansing dan maar:
Deze post bij gebrek aan openstaande wiskundevragen, zoals al lange tijd steeds het geval is als ik in dit topic kijk. .
.
Edit: even googlen levert bijv. het volgende op, uit een "Samenvatting Wiskunde Leerboek 1 getal en ruimte examenstof": "Het open interval <6,13> is het gedeelte van de getallenlijn tussen 6 en 13.". Het lijkt dus inderdaad om notatie uit (in ieder geval) Getal & Ruimte te gaan.
[ Bericht 6% gewijzigd door keesjeislief op 14-09-2009 01:56:15 ]
Ik herinner me die notatie wel ergens van, waarschijnlijk van mijn middelbare schooltijd, wij gebruikten Getal & Ruimte, misschien dat het daar (o.a.) vandaan komt?quote:Op zondag 13 september 2009 21:50 schreef Iblis het volgende:
[..]
Goede vraag. Ik denk dat ik dat per ongeluk fout heb ingesteld op m’n toetsenbord. Alhoewel ik meestal \rangle gebruik: [ afbeelding ]. Bij de volgende revisie zal ik dat fiksen.
Deze post bij gebrek aan openstaande wiskundevragen, zoals al lange tijd steeds het geval is als ik in dit topic kijk.
Edit: even googlen levert bijv. het volgende op, uit een "Samenvatting Wiskunde Leerboek 1 getal en ruimte examenstof": "Het open interval <6,13> is het gedeelte van de getallenlijn tussen 6 en 13.". Het lijkt dus inderdaad om notatie uit (in ieder geval) Getal & Ruimte te gaan.
[ Bericht 6% gewijzigd door keesjeislief op 14-09-2009 01:56:15 ]
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


Klopt, daar wordt dat zo gebruikt.quote:Op maandag 14 september 2009 01:40 schreef keesjeislief het volgende:
Shit, gooi ik met die nutteloze post ook het topic nog dicht. In de herkansing dan maar:
[..]
Ik herinner me die notatie wel ergens van, waarschijnlijk van mijn middelbare schooltijd, wij gebruikten Getal & Ruimte, misschien dat het daar (o.a.) vandaan komt?
Deze post bij gebrek aan openstaande wiskundevragen, zoals al lange tijd steeds het geval is als ik in dit topic kijk..
Edit: even googlen levert bijv. het volgende op, uit een "Samenvatting Wiskunde Leerboek 1 getal en ruimte examenstof": "Het open interval <6,13> is het gedeelte van de getallenlijn tussen 6 en 13.". Het lijkt dus inderdaad om notatie uit (in ieder geval) Getal & Ruimte te gaan.
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Weer wat geleerd. Ik heb in ieder geval m’n keyboard layout aangepast, zodat ik ⟨–∞,+∞⟩ de juiste haakjes kan gebruiken en Riparius me niet meer hoeft te corrigeren. 
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Hoop dat iemand me een zetje in de goede richting kan geven, weet namelijk echt niet waar ik moet beginnen.
Gegeven een iteratieproces van een vispopulatie:
t(n+1) = t(n) * e^(k(a-t(n)))
Laat zien dat de geschaalde variabele y(n) = t(n) / a voldoet aan:
y(n+1) = y(n) * e^(K(1-y(n)))
(K is hier een andere variabele dan k in de eerste vergelijking)
(Heb het geprobeerd in het latex ding van glowmouse te zetten maar daar kwam de macht niet echt lekker uit)
Gegeven een iteratieproces van een vispopulatie:
t(n+1) = t(n) * e^(k(a-t(n)))
Laat zien dat de geschaalde variabele y(n) = t(n) / a voldoet aan:
y(n+1) = y(n) * e^(K(1-y(n)))
(K is hier een andere variabele dan k in de eerste vergelijking)
(Heb het geprobeerd in het latex ding van glowmouse te zetten maar daar kwam de macht niet echt lekker uit)


Je moest waarschijnlijk e^{...} typen, om aan te geven wat allemaal in de exponent moest. Hoe dan ook als y(n) = t(n)/a, dan krijg je:
Bovenstaande hebben we gewoon verkregen door y(n) door t(n)/a te vervangen. Nu gaan we in de exponent eens die 1/a buiten haakjes halen, dan krijgen we:
Ik neem aan dat K/a = k, dus dat we dat kunnen vervangen, en dan krijgen we:
En laat de rechterkant nu precies gelijk zijn aan t(n + 1)/a:
Bovenstaande hebben we gewoon verkregen door y(n) door t(n)/a te vervangen. Nu gaan we in de exponent eens die 1/a buiten haakjes halen, dan krijgen we:
Ik neem aan dat K/a = k, dus dat we dat kunnen vervangen, en dan krijgen we:
En laat de rechterkant nu precies gelijk zijn aan t(n + 1)/a:
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


[edit] Laat maar, zie het al  bedankt! [/edit]
bedankt! [/edit]
[ Bericht 70% gewijzigd door woopehh op 14-09-2009 12:45:01 ]
[ Bericht 70% gewijzigd door woopehh op 14-09-2009 12:45:01 ]


De exponenten zijn hetzelfde. Als je met de bovenste begint, deel dan K door a en vermenigvuldig 1-t(n)/a met a om bij de onderste uit te komen. Je haalt een 1/a buiten haakjes, om het anders te zeggen.quote:Op maandag 14 september 2009 12:39 schreef woopehh het volgende:
Bedankt, snap alleen niet echt hoe je van:
[ afbeelding ]
naar
[ afbeelding ]
gaat, zou je dat nog kunnen toelichten?
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


Indien verdeeld is, voor welke waarde van x geldt dat de kans
Ik heb het geprobeerd met z-transformatie, maar dat lukt me niet:
(kortom, ik hou weer gewoon -x+2 over...)
Ik snap er echt helemaal niets van!
Ik heb het geprobeerd met z-transformatie, maar dat lukt me niet:
(kortom, ik hou weer gewoon -x+2 over...)
Ik snap er echt helemaal niets van!


Maar je hebt nu een andere x. Nu moet je in een tabel de z-waarde opzoeken.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ohja, vergeten te zeggen.. Dat heb ik gedaan, maar de tabel die ik erbij heb gekregen gaat maar tot z=3,0...quote:Op dinsdag 15 september 2009 18:51 schreef GlowMouse het volgende:
Maar je hebt nu een andere x. Nu moet je in een tabel de z-waarde opzoeken.
Ik dacht eerst dat ik moest kijken bij z=5 (van 5%) maar dat staat dus niet in de tabel...


Je zoekt nu op P(Z < 0.95). Ik wil c zodanig dat P(Z<c) = 0.95.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Uh.. ja dat snap ik, dat was ook de opgave: ..quote:Op dinsdag 15 september 2009 19:21 schreef GlowMouse het volgende:
Ik wil c zodanig dat P(Z<c) = 0.95.
Ik heb alleen dus echt geen flauw idee hoe ik dat doe...


Je weet toch hoe deze curve werkt?quote:Op dinsdag 15 september 2009 19:26 schreef Booomer het volgende:
[..]
Uh.. ja dat snap ik, dat liet ik hier al zien [ afbeelding ]..
Ik heb alleen dus echt geen flauw idee hoe ik dat doe...
Bron: Wikimedia Commons. Maker: Jeremy Kemp. Licentie: CC-BY.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ja, ik moet het punt (-x+2) vinden waarop 95% binnen de curve valt.. Maar hoe weet ik dus niet, zoals ik nu al meerdere keren heb gezegd. Kan niemand het nou gewoon even uitleggen? 
[ Bericht 33% gewijzigd door Booomer op 15-09-2009 19:51:52 ]
[ Bericht 33% gewijzigd door Booomer op 15-09-2009 19:51:52 ]


Gewoon opzoeken in een tabel: http://www.math.unb.ca/~knight/utility/NormTble.htm.quote:Op dinsdag 15 september 2009 19:46 schreef Booomer het volgende:
Ja, ik moet het punt (-x+2) vinden waarop 95% binnen de curve valt.. Maar hoe weet ik dus niet, zoals ik nu al meerdere keren heb gezegd. Kan niemand het nou gewoon even uitleggen?
Kijk voor welke waarde van Z je een kans 0.95 krijgt.
Je gaat eerst naar beneden in de tabel, verticaal dus. Dan zie je dat je voor Z=1.6 de waarde 0.9452 krijgt en voor Z=1.7 de waarde 0.9554. De laatste waarde is te hoog, dus zoek je verder in de rij van Z=1.6. Je gaat nu dus horizontaal kijken. Dan zie je dat je voor Z=1.64 de waarde 0.9495 en voor Z=1.65 de waarde 0.9505 krijgt. De gevraagde kans van 0.95 ligt hier precies tussen in dus neem je als benadering Z=1.645.
Nu geldt: Z = -x + 2
x = 2 - 1.645 = 0.355


Huh, dat is een hele andere tabel als die ik erbij heb gekregen. Die van mij loopt bij z=0,00 (0,5000) af naar z=3,09 (0,0010). Hierin kan ik dus niet eens een kans 0,95 opzoeken. 


Maar wat zégt die tabel? Waarnaar gelinkt wordt geeft de ‘Probability content from -∞ to Z’. Die van jou van Z naar +∞ waarschijnlijk. Want z = 3,09 geeft 0,9990 in die tabel, en 0,0010 + 0,9990 = 1. Daarom mijn vraag: weet je hoe die curve werkt?quote:Op dinsdag 15 september 2009 20:07 schreef Booomer het volgende:
Huh, dat is een hele andere tabel als die ik erbij heb gekregen. Die van mij loopt bij z=0,00 (0,5000) af naar z=3,09 (0,0010). Hierin kan ik dus niet eens een kans 0,95 opzoeken.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ben ik alweer, mis jammer genoeg nog steeds wat colleges door ziekte en wil niet graag achter komen 
Teken een blok waarbij O de oorsprong is; a, b en c zijn de vectoren bij A, B en C. Druk het volgende uit in a, b en c.
Nu de misschien heel domme vraag.. wat bedoelen ze in hemelsnaam met dat blok? Misschien dat ik dan de rest van de vraag wel snap
Misschien dat ik dan de rest van de vraag wel snap 
Teken een blok waarbij O de oorsprong is; a, b en c zijn de vectoren bij A, B en C. Druk het volgende uit in a, b en c.
Nu de misschien heel domme vraag.. wat bedoelen ze in hemelsnaam met dat blok?


Denk het. Heel die curve = 1, en gevraagd werd op welk punt je 95% hebt. Bedankt mrbombastic, dankzij jou ben ik eruit gekomen!quote:Op dinsdag 15 september 2009 20:11 schreef Iblis het volgende:
[..]
Maar wat zégt die tabel? Waarnaar gelinkt wordt geeft de ‘Probability content from -∞ to Z’. Die van jou van Z naar +∞ waarschijnlijk. Want z = 3,09 geeft 0,9990 in die tabel, en 0,0010 + 0,9990 = 1. Daarom mijn vraag: weet je hoe die curve werkt?



Die notatie is echt zo? Ik zit ook even te twijfelen, maar bedoelen ze niet gewoon wat ik een balk zou noemen?quote:Op dinsdag 15 september 2009 20:13 schreef woopehh het volgende:
Ben ik alweer, mis jammer genoeg nog steeds wat colleges door ziekte en wil niet graag achter komen
Teken een blok [ afbeelding ] waarbij O de oorsprong is; a, b en c zijn de vectoren bij A, B en C. Druk het volgende uit in a, b en c.
Nu de misschien heel domme vraag.. wat bedoelen ze in hemelsnaam met dat blok?Misschien dat ik dan de rest van de vraag wel snap
Bron: Wikimedia Commons. Maker: Svdmolen. Publiek Domein.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.

 verdeeld is, voor welke waarde van x geldt dat de kans
verdeeld is, voor welke waarde van x geldt dat de kans 
 (kortom, ik hou weer gewoon -x+2 over...)
(kortom, ik hou weer gewoon -x+2 over...)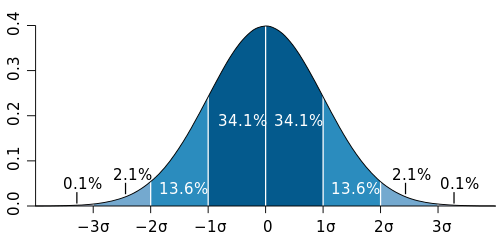
 waarbij O de oorsprong is; a, b en c zijn de vectoren bij A, B en C. Druk het volgende uit in a, b en c.
waarbij O de oorsprong is; a, b en c zijn de vectoren bij A, B en C. Druk het volgende uit in a, b en c.