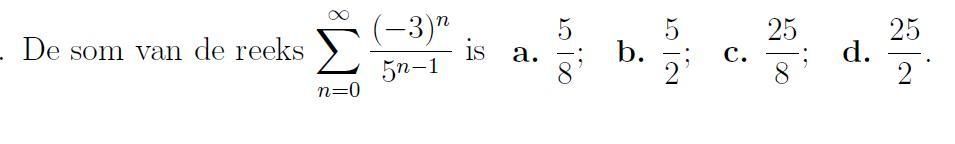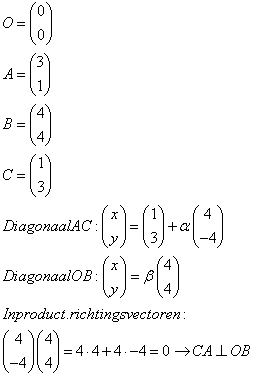SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Vorige deel: [Bèta wiskunde] 'Huiswerk- en vragentopic'.
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
http://betahw.mine.nu/index.php: site van GlowMouse om formules te kunnen gebruiken in je posts (op basis van Latexcode wordt een plaatje gegenereerd dat je vervolgens via het aangegeven linkje kunt opnemen).
Wiskundig inhoudelijk:
http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
OP
[ Bericht 2% gewijzigd door GlowMouse op 31-03-2009 21:38:11 ]
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
Wiskundig inhoudelijk:
OP
[ Bericht 2% gewijzigd door GlowMouse op 31-03-2009 21:38:11 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


tvp
There is but one straight course, and that is to seek truth and pursue it steadily. - George Washington
*** Wiskunde Meisjes Blog *** CFR.org *** NRC.nl ***
*** Wiskunde Meisjes Blog *** CFR.org *** NRC.nl ***


Ben ik weer 
Ja weer reeksen/rijen, kheb de stof al aardig onder de knie, alleen deze nog niet, terwijl het altijd de eerste vragen van het tentamen zijn

Ik doe het zo.
Dit "moet" kloppen, want als ik beide rijen in mijn gr invoer komen er dezelfde antwoorden uit.
Dus zou de som deze meetkundige rij -3/(1+(3/5)) zijn toch? Maar dat geeft -15/8 als antwoord. wat er niet tussen staat.
Wat doe ik fout?
alvast bedankt
[ Bericht 5% gewijzigd door motorbloempje op 01-09-2013 20:47:37 ]
Ja weer reeksen/rijen, kheb de stof al aardig onder de knie, alleen deze nog niet, terwijl het altijd de eerste vragen van het tentamen zijn
Ik doe het zo.
Dit "moet" kloppen, want als ik beide rijen in mijn gr invoer komen er dezelfde antwoorden uit.
Dus zou de som deze meetkundige rij -3/(1+(3/5)) zijn toch? Maar dat geeft -15/8 als antwoord. wat er niet tussen staat.
Wat doe ik fout?
alvast bedankt
[ Bericht 5% gewijzigd door motorbloempje op 01-09-2013 20:47:37 ]
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


Je reeks is met termen tot de macht n-1, maar de somformule die je toepast is voor termen tot de macht n. In plaats van een factor 3 naar voren te halen had je dus beter een factor 5 naar voren kunnen halen.


Ik begrijp niet precies wat je bedoelt. Maar ik zie wel in dat de eerste term 5 = en niet 3 zoals ik al dacht. Omdat de reeks met n=0 begint --> Ao = 5. (Dat bedoel je zeker ookquote:Op woensdag 25 maart 2009 22:32 schreef thabit het volgende:
Je reeks is met termen tot de macht n-1, maar de somformule die je toepast is voor termen tot de macht n. In plaats van een factor 3 naar voren te halen had je dus beter een factor 5 naar voren kunnen halen.
Dan klopt die rijverhouding ook niet. Dan is het wel 5/(1+(3/5)) = 25/8 (en dat is het goede antwoord)
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


quote:Op dinsdag 24 maart 2009 13:24 schreef GlowMouse het volgende:
Gebruik \frac{teller}{noemer} voor breuken, anders kun je net zo goed geen tex gebruiken.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


-
[ Bericht 99% gewijzigd door motorbloempje op 01-09-2013 20:47:56 ]
[ Bericht 99% gewijzigd door motorbloempje op 01-09-2013 20:47:56 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Het kan uiteraard op verschillende manieren, maar je hoeft niet eens een factor voor het somteken te halen. Kijk eerst wat de eerste term a van je reeks is, die krijg je hier door n=0 te nemen. Kijk dan wat de reden r is. De som van je (convergente) reeks is dan a/(1-r).quote:Op woensdag 25 maart 2009 22:38 schreef Agiath het volgende:
[..]
Ik begrijp niet precies wat je bedoelt. Maar ik zie wel in dat de eerste term 5 = en niet 3 zoals ik al dacht. Omdat de reeks met n=0 begint --> Ao = 5. (Dat bedoel je zeker ook)
Dan klopt die rijverhouding ook niet. Dan is het wel 5/(1+(3/5)) = 25/8 (en dat is het goede antwoord)


Zo kan het natuurlijk ook, bedanktquote:
Ik snap het, bedankt.quote:Op woensdag 25 maart 2009 22:42 schreef Riparius het volgende:
[..]
Het kan uiteraard op verschillende manieren, maar je hoeft niet eens een factor voor het somteken te halen. Kijk eerst wat de eerste term a van je reeks is, die krijg je hier door n=0 te nemen. Kijk dan wat de reden r is. De som van je (convergente) reeks is dan a/(1-r).
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


OK. Uitwerking van je opgave van gisteren ook gesnapt? Want die was toch iets lastiger dan een simpele meetkundige reeks sommeren.quote:Op woensdag 25 maart 2009 22:47 schreef Agiath het volgende:
[..]
Zo kan het natuurlijk ook, bedankt
[..]
Ik snap het, bedankt.


Ja, net nog even grondig doorgelezen en ik snap het helemaal. Bedanktquote:Op woensdag 25 maart 2009 22:49 schreef Riparius het volgende:
[..]
OK. Uitwerking van je opgave van gisteren ook gesnapt? Want die was toch iets lastiger dan een simpele meetkundige reeks sommeren.
En ik blijf zeggen dat ik die dingen (limit comparison test) nog steeds makkelijker vind dan die sommen.
Maargoed het is 11 uur geweest en het is mooi geweest voor vandaag.
Ik denk dat ik morgen misschien nog wel terug kom met wat vraagjes
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


Even een vraagje over gegevens in mijn Casio TI-83.
Ik heb zojuist een normale functie ingevuld bij Y1 en nu wil ik daar een grafiek bij hebben. Ik heb de juiste window-waarden genomen, maar hij geeft een soort puntgrafiek weer. Ik wil helemaal geen puntgrafiek, ik wil een normale lijngrafiek!
Kan iemand mij helpen de grafiek te veranderen?
Ik heb zojuist een normale functie ingevuld bij Y1 en nu wil ik daar een grafiek bij hebben. Ik heb de juiste window-waarden genomen, maar hij geeft een soort puntgrafiek weer. Ik wil helemaal geen puntgrafiek, ik wil een normale lijngrafiek!
Kan iemand mij helpen de grafiek te veranderen?
hier kommt die Sonne!
alias Idril-2, alias anneVi
alias Idril-2, alias anneVi


Ja ik weet hoe dit moet.quote:Op donderdag 26 maart 2009 19:21 schreef anne_Chris het volgende:
Even een vraagje over gegevens in mijn Casio TI-83.
Ik heb zojuist een normale functie ingevuld bij Y1 en nu wil ik daar een grafiek bij hebben. Ik heb de juiste window-waarden genomen, maar hij geeft een soort puntgrafiek weer. Ik wil helemaal geen puntgrafiek, ik wil een normale lijngrafiek!
Kan iemand mij helpen de grafiek te veranderen?
Ga met je 'cursor' helemaal links van Y1 staan en daar kan je kiezen wat voor grafiek je wilt hebben. (dik dun, lijntjes etc.)
Gewoon weer op dun lijntje zetten daar
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


Vector rekenen. Het zal wel heel simpel zijn maar ik weet dus niet wat ik moet doen:
Met hoofdletters bedoel ik punten, met kleine letters vectoeren.
De vragen:
a) Als hoekpunten A,B,C van driehoek ABC in het platte vlak worden geïdentificeerd met de positievectoren a,b,c, dan blijkt het punt (a+b+c)/3 op de zwaartelijn vanuit A te liggen. Reken na.Conclusie?
Mijn antwoord: in principe gaat het er om om dmv van vectoren aan te tonen dat het zwaartepunt van de driehoek op de zwaartelijn vanuit A ligt.
Positievector begint vanuit O. Ik heb a/3+b/3+c/3 getrokken. De genoemde zwaartelijn zal moeten zijn a+labda*(0,5b+0,5c-a). a is de steunvector en 0,5b-0,5c - a is de richtinsvector van de lijn. Dan heb ik een vergelijking van een lijn in vectoren en een punt. Hoe verder of heb ik de verkeerde aanpak. Ik zie niet wat ik doen moet.
b) Als hoekpunten punten A,B,C,D in de ruimte worden geïdentificeerd met de positievectoren a,b,c,d dan blijkt het punt (a+b+c+d)/4 te liggen op de lijn vanuit A naar het zwaartepunt van driehoek BCD. Reken na! Conclusie?
Ook hier. Zwaartepunt van een driehoek is a/3+b/3+c/3. Lijn van a naar het zwaartepunt heeft dan ri. vector a/3+b/3-c/3 - a. En dus is de vlg van de lijn a (steunvector+ richtingsvector) a+labda*( a/3+b/3-c/3 - a).....
Hoe zit dit?!
[ Bericht 11% gewijzigd door Borizzz op 26-03-2009 21:04:55 ]
Met hoofdletters bedoel ik punten, met kleine letters vectoeren.
De vragen:
a) Als hoekpunten A,B,C van driehoek ABC in het platte vlak worden geïdentificeerd met de positievectoren a,b,c, dan blijkt het punt (a+b+c)/3 op de zwaartelijn vanuit A te liggen. Reken na.Conclusie?
Mijn antwoord: in principe gaat het er om om dmv van vectoren aan te tonen dat het zwaartepunt van de driehoek op de zwaartelijn vanuit A ligt.
Positievector begint vanuit O. Ik heb a/3+b/3+c/3 getrokken. De genoemde zwaartelijn zal moeten zijn a+labda*(0,5b+0,5c-a). a is de steunvector en 0,5b-0,5c - a is de richtinsvector van de lijn. Dan heb ik een vergelijking van een lijn in vectoren en een punt. Hoe verder of heb ik de verkeerde aanpak. Ik zie niet wat ik doen moet.
b) Als hoekpunten punten A,B,C,D in de ruimte worden geïdentificeerd met de positievectoren a,b,c,d dan blijkt het punt (a+b+c+d)/4 te liggen op de lijn vanuit A naar het zwaartepunt van driehoek BCD. Reken na! Conclusie?
Ook hier. Zwaartepunt van een driehoek is a/3+b/3+c/3. Lijn van a naar het zwaartepunt heeft dan ri. vector a/3+b/3-c/3 - a. En dus is de vlg van de lijn a (steunvector+ richtingsvector) a+labda*( a/3+b/3-c/3 - a).....
Hoe zit dit?!
[ Bericht 11% gewijzigd door Borizzz op 26-03-2009 21:04:55 ]
kloep kloep


Het is b/2 + c/2 - a, niet b/2 - c/2 - a. Vervolgens vul je lambda=2/3 in.quote:Op donderdag 26 maart 2009 20:21 schreef Borizzz het volgende:
Vector rekenen. Het zal wel heel simpel zijn maar ik weet dus niet wat ik moet doen:
Met hoofdletters bedoel ik punten, met kleine letters vectoeren.
De vragen:
a) Als hoekpunten A,B,C van driehoek ABC in het platte vlak worden geïdentificeerd met de positievectoren a,b,c, dan blijkt het punt (a+b+c)/3 op de zwaartelijn vanuit A te liggen. Reken na.Conclusie?
Mijn antwoord: in principe gaat het er om om dmv van vectoren aan te tonen dat het zwaartepunt van de driehoek op de zwaartelijn vanuit A ligt.
Positievector begint vanuit O. Ik heb a/3+b/3+c/3 getrokken. De genoemde zwaartelijn zal moeten zijn a+labda*(0,5b+0,5c-a). a is de steunvector en 0,5b-0,5c - a is de richtinsvector van de lijn. Dan heb ik een vergelijking van een lijn in vectoren en een punt. Hoe verder of heb ik de verkeerde aanpak. Ik zie niet wat ik doen moet.


Waarom dan labda=2/3? Dit komt voor mij uit de lucht vallen... Kun je die uitrekenen.quote:Op donderdag 26 maart 2009 21:35 schreef thabit het volgende:
[..]
Het is b/2 + c/2 - a, niet b/2 - c/2 - a. Vervolgens vul je lambda=2/3 in.
Of heeft dit de maken met het feit dat labda willekeurig is en dat verschillende waarden van labda verschillende punten op de lijn aanwijzen. En dan labda=2/3 dan ingevuld in de vergelijking het punt a/3 + b/3 + c/3 aanwijst?
kloep kloep


Wel, de coefficienten van a, b en c moeten alle drie gelijk worden gemaakt aan 1/3. Er staat a - lambda*a + ... . Dus moet lambda = 2/3 gelden en dan zijn na inspectie ook de coefficienten van b en c correct.quote:Op donderdag 26 maart 2009 21:37 schreef Borizzz het volgende:
[..]
Waarom dan labda=2/3? Dit komt voor mij uit de lucht vallen... Kun je die uitrekenen.
Of heeft dit de maken met het feit dat labda willekeurig is en dat verschillende waarden van labda verschillende punten op de lijn aanwijzen. En dan labda=2/3 dan ingevuld in de vergelijking het punt a/3 + b/3 + c/3 aanwijst?


Ok dank je. De b) vraag zal dan wel op een vergelijkbare manier gaan.quote:Op donderdag 26 maart 2009 21:41 schreef thabit het volgende:
[..]
Wel, de coefficienten van a, b en c moeten alle drie gelijk worden gemaakt aan 1/3. Er staat a - lambda*a + ... . Dus moet lambda = 2/3 gelden en dan zijn na inspectie ook de coefficienten van b en c correct.
kloep kloep


Ik denk niet dat dit de bedoeling is, want concluderen dat het zwaartepunt op de zwaartelijn vanuit A ligt is een dooddoener. Het zwaartepunt in een driehoek is het snijpunt van de zwaartelijnen, en natuurlijk ligt het zwaartepunt dan op elk van de zwaartelijnen. Volgens mij is het eerder de bedoeling dat je op grond van symmetrie-overwegingen hieruit concludeert dat het bedoelde punt op elk van de drie zwaartelijnen vanuit A, B en C ligt, en dat de drie zwaartelijnen dus door één punt gaan. Een soort vectorbewijs dus voor de stelling uit de elementaire meetkunde dat de drie zwaartelijnen van een driehoek door één punt gaan.quote:Op donderdag 26 maart 2009 20:21 schreef Borizzz het volgende:
Vector rekenen. Het zal wel heel simpel zijn maar ik weet dus niet wat ik moet doen:
Met hoofdletters bedoel ik punten, met kleine letters vectoeren.
De vragen:
a) Als hoekpunten A,B,C van driehoek ABC in het platte vlak worden geïdentificeerd met de positievectoren a,b,c, dan blijkt het punt (a+b+c)/3 op de zwaartelijn vanuit A te liggen. Reken na.Conclusie?
Mijn antwoord: in principe gaat het er om om dmv van vectoren aan te tonen dat het zwaartepunt van de driehoek op de zwaartelijn vanuit A ligt.
Een vectorvoorstelling van de zwaartelijn door A is inderdaad za = a + λ∙(½∙b + ½∙c - a). Voor λ = 0 zit je in punt A en voor λ = 1 in het midden van lijnstuk BC.quote:Positievector begint vanuit O. Ik heb a/3+b/3+c/3 getrokken. De genoemde zwaartelijn zal moeten zijn a+labda*(0,5b+0,5c-a). a is de steunvector en 0,5b+0,5c - a is de richtingsvector van de lijn. Dan heb ik een vergelijking van een lijn in vectoren en een punt. Hoe verder of heb ik de verkeerde aanpak. Ik zie niet wat ik doen moet.
Je weet ook uit de elementaire meetkunde dat twee zwaartelijnen in een driehoek elkaar verdelen in de verhouding 2:1met het langste stuk aan de kant van het hoekpunt, dus voor λ = 2/3 zit je in het zwaartepunt. En inderdaad is a + 2/3∙(½∙b + ½∙c - a) = 1/3∙a + 1/3∙ b + 1/3∙c. Zo, nu mag je zelf weer even verder puzzelen ...
[ Bericht 0% gewijzigd door Riparius op 26-03-2009 22:00:05 ]


ff checken
If A is the area of a circle with radius r and the circle expands as time passes, find dA/dt in terms of dr/dt.
dA/dt = pi * (dr/dt)^2
Is dit het goede antwoord?
If A is the area of a circle with radius r and the circle expands as time passes, find dA/dt in terms of dr/dt.
dA/dt = pi * (dr/dt)^2
Is dit het goede antwoord?


hoi,
ik moet voor een wiskunde po de naam geven van een ruimtelijk figuur, eentje heb ik al gevonden maar de andere zou ik echt niet weten.
even een korte beschrijving van het figuur:
het gaat om een afgeknotte piramide (4 hoeken) met daarop nog een piramide.
dat is de afgeknotte piramide
en deze zit er dan bovenop:
alvast bedankt!
ik moet voor een wiskunde po de naam geven van een ruimtelijk figuur, eentje heb ik al gevonden maar de andere zou ik echt niet weten.
even een korte beschrijving van het figuur:
het gaat om een afgeknotte piramide (4 hoeken) met daarop nog een piramide.
dat is de afgeknotte piramide
en deze zit er dan bovenop:
alvast bedankt!
no time to waste


Deze deelvraag is hiermee toch klaar? Want je toont aan door labmda=2/3 te kiezen dat het bewuste punt op de lijn ligt en dat was de vraag. Of doel je hiermee op de tweede vraag? Die is overigens nu wel gelukt.quote:Op donderdag 26 maart 2009 21:52 schreef Riparius het volgende:
Je weet ook uit de elementaire meetkunde dat twee zwaartelijnen in een driehoek elkaar verdelen in de verhouding 2:1met het langste stuk aan de kant van het hoekpunt, dus voor λ = 2/3 zit je in het zwaartepunt. En inderdaad is a + 2/3∙(½∙b + ½∙c - a) = 1/3∙a + 1/3∙ b + 1/3∙c. Zo, nu mag je zelf weer even verder puzzelen ...
kloep kloep


Ja, de eerste deelvraag was in feite klaar en ik bedoelde inderdaad dat je nu zelf wel verder kon met de tweede deelvraag. Maar je zei hierboven ook dat λ = 2/3 voor jou uit de lucht kwam vallen terwijl dat natuurlijk niet zo is. Ik wilde even laten zien dat die waarde voor λ de bekende stelling weerspiegelt dat twee zwaartelijnen in een driehoek elkaar verdelen in de verhouding 2:1.quote:Op vrijdag 27 maart 2009 17:53 schreef Borizzz het volgende:
[..]
Deze deelvraag is hiermee toch klaar? Want je toont aan door labmda=2/3 te kiezen dat het bewuste punt op de lijn ligt en dat was de vraag. Of doel je hiermee op de tweede vraag? Die is overigens nu wel gelukt.


Ja prima. Maar het is nu duidelijk. Maar het meetkundige verband had ik inderdaad al door. Ik heb nu wel even iets geleerd over het gebruik van lijnen die in vectornotatie staan.quote:Op vrijdag 27 maart 2009 18:08 schreef Riparius het volgende:
[..]
Ja, de eerste deelvraag was in feite klaar en ik bedoelde inderdaad dat je nu zelf wel verder kon met de tweede deelvraag. Maar je zei hierboven ook dat λ = 2/3 voor jou uit de lucht kwam vallen terwijl dat natuurlijk niet zo is. Ik wilde even laten zien dat die waarde voor λ de bekende stelling weerspiegelt dat twee zwaartelijnen in een driehoek elkaar verdelen in de verhouding 2:1.
kloep kloep


Nog zoiets: een ruit en dan met vectoren laten zien dat diagonalen loodreacht staan.
Ik heb de ruit gedefinieerd met positievectoren a b c en d.
de beide diagonalen hebben dan richtingsvectoren c-a en d-b.
volgens mij gaat het er dan om dat je laat zien dat het inproduct van deze 2 richtingsvectoren 0 is.
dus (c-a)(d-b) =0 aantonen
levert mij (c-a)(d-b) = cd-cb-ad+ab = c(d-b) -a(d-b).
Maar dan ben ik er nog niet..
Ik heb de ruit gedefinieerd met positievectoren a b c en d.
de beide diagonalen hebben dan richtingsvectoren c-a en d-b.
volgens mij gaat het er dan om dat je laat zien dat het inproduct van deze 2 richtingsvectoren 0 is.
dus (c-a)(d-b) =0 aantonen
levert mij (c-a)(d-b) = cd-cb-ad+ab = c(d-b) -a(d-b).
Maar dan ben ik er nog niet..
kloep kloep


Een inproduct noteer ik als <x,y>. Bij een ruit zijn alle zijden even lang. Dus
<a-b, a-b> = <a-d, a-d> = <c-b, c-b> = <c-d, c-d>.
Als we de eerste gelijkheid uitwerken krijgen we
<a,a> - 2<a,b> + <b,b> = <a,a> - 2<a,d> + <d,d>.
ofwel
<b,b> - <d,d> = 2<a,b> - 2<a,d> = 2<a,b-d>
En bij de laatste gelijkheid krijgen we
<c,c> - 2<c,b> + <b,b> = <c,c> - 2<c,d> + <d,d>.
ofwel
<b,b> - <d,d> = 2<c,b-d>.
We zien dus <a,b-d> = <c,b-d> en als we dit naar 1 kant gooien staat er
<a-c, b-d> = <a, b-d> - <c,b-d> = 0.
<a-b, a-b> = <a-d, a-d> = <c-b, c-b> = <c-d, c-d>.
Als we de eerste gelijkheid uitwerken krijgen we
<a,a> - 2<a,b> + <b,b> = <a,a> - 2<a,d> + <d,d>.
ofwel
<b,b> - <d,d> = 2<a,b> - 2<a,d> = 2<a,b-d>
En bij de laatste gelijkheid krijgen we
<c,c> - 2<c,b> + <b,b> = <c,c> - 2<c,d> + <d,d>.
ofwel
<b,b> - <d,d> = 2<c,b-d>.
We zien dus <a,b-d> = <c,b-d> en als we dit naar 1 kant gooien staat er
<a-c, b-d> = <a, b-d> - <c,b-d> = 0.


Op die manier had ik het nog niet bekeken.
Maar ik had al een andere oplossing. Kan deze ook?
Een vierhoek heeft 4 gelijke zijden. stel vector a als een zijde en ook vector b als een zijde.
De diagonalen van deze vierhoek zijn dan (a+b) en (a-b).
Het inproduct van deze 2 is dan (a+b)(a-b) = a2 - b2.
Een eigenschap van vectoren is dat x2 = | x| 2.
dus er geldt dat (a+b)(a-b) = |a|2 - |b|2.
aangezien a en b dezelfde lengte voorstellen geldt (a+b)(a-b) = 0.
Maar ik had al een andere oplossing. Kan deze ook?
Een vierhoek heeft 4 gelijke zijden. stel vector a als een zijde en ook vector b als een zijde.
De diagonalen van deze vierhoek zijn dan (a+b) en (a-b).
Het inproduct van deze 2 is dan (a+b)(a-b) = a2 - b2.
Een eigenschap van vectoren is dat x2 = | x| 2.
dus er geldt dat (a+b)(a-b) = |a|2 - |b|2.
aangezien a en b dezelfde lengte voorstellen geldt (a+b)(a-b) = 0.
kloep kloep


Je gebruikt daar wel dat tegenover elkaar liggende diagonalen evenwijdig zijn. Ik neem aan dat dat niet in de definitie van een ruit zit?


Naja even de vraag goed herlezend: het ging om een vierhoek met evenlange zijden en tegenoverliggende zijden parallel.quote:Op vrijdag 27 maart 2009 21:19 schreef thabit het volgende:
Je gebruikt daar wel dat tegenover elkaar liggende diagonalen evenwijdig zijn. Ik neem aan dat dat niet in de definitie van een ruit zit?
kloep kloep


A street light is mounted at the top of a 15-ft-tall pole. A man 6ft tall walks away from the pole with a speed of 5 ft/s along a straight path. How fast is the tip of his shadow moving when he is 40ft from the pole?
Hoe bereken ik ook alweer waar de tip van his schaduw precies is? Dus niet het antwoord op de vraag, maar gewoon waar de tip van de schaduw is met betrekking tot de lantaarnpaal.
Hoe bereken ik ook alweer waar de tip van his schaduw precies is? Dus niet het antwoord op de vraag, maar gewoon waar de tip van de schaduw is met betrekking tot de lantaarnpaal.


Levensverzekeringswiskunde is een stom vak }:|
Goed, bij een opgave moet ik de P berekenen en tot nu toe heb ik dit:
¤ 10.000 + p * 13,41675982 = ¤ 50.000 * 0,351457202
Wat neer zou moeten komen op
¤ 10.000 + p * 13,41675982 = ¤ 17.572,8601
Maar ik snap niet wat ik nu met die ¤ 10.000 moet doen :o
Het antwoordenboek zegt dit:
Maar wat ik ook doe, ik kom niet uit op ¤ 564,43 :N Wie heeft het verlossende antwoord?
Goed, bij een opgave moet ik de P berekenen en tot nu toe heb ik dit:
¤ 10.000 + p * 13,41675982 = ¤ 50.000 * 0,351457202
Wat neer zou moeten komen op
¤ 10.000 + p * 13,41675982 = ¤ 17.572,8601
Maar ik snap niet wat ik nu met die ¤ 10.000 moet doen :o
Het antwoordenboek zegt dit:
| 1 2 3 | 10.000 + p x ((503.387 – 167.324)/25.048) = 50.000 x (8.803,3/ 25.048) p = 564,43 |
Maar wat ik ook doe, ik kom niet uit op ¤ 564,43 :N Wie heeft het verlossende antwoord?
Verily i say unto you; dost thou even hoist, brethren? - Jesus (Psalm 22)


Dit is niet goed voor mijn zelfvertrouwen, maar bedanktquote:Op zondag 29 maart 2009 19:05 schreef GlowMouse het volgende:
http://www.fi.uu.nl/toepassingen/02017/toepassing_wisweb.html
Verily i say unto you; dost thou even hoist, brethren? - Jesus (Psalm 22)


Ik vind het wel een mooie appletquote:Op zondag 29 maart 2009 19:06 schreef Maraca het volgende:
[..]
Dit is niet goed voor mijn zelfvertrouwen, maar bedankt
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


is het ookquote:
Verily i say unto you; dost thou even hoist, brethren? - Jesus (Psalm 22)


ik ben bezig met vergelijkingen oefenen voor statica, maar deze snap ik echt niet;
12/13A -A is gelijk aan 25/13 A
het zal vast heel makkelijk zijn maar...
12/13A -A is gelijk aan 25/13 A
het zal vast heel makkelijk zijn maar...


Moet dat geen 12/13A + A zijn?
12/13A + A = (12/13 + 1)A
En dan http://proto.thinkquest.nl/~klb045/h2-broptellen.html
12/13A + A = (12/13 + 1)A
En dan http://proto.thinkquest.nl/~klb045/h2-broptellen.html
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


quote:Op zondag 29 maart 2009 18:51 schreef Maraca het volgende:
Levensverzekeringswiskunde is een stom vak
Goed, bij een opgave moet ik de P berekenen en tot nu toe heb ik dit:
¤ 10.000 + p * 13,41675982 = ¤ 50.000 * 0,351457202
Wat neer zou moeten komen op
¤ 10.000 + p * 13,41675982 = ¤ 17.572,8601
Maar ik snap niet wat ik nu met die ¤ 10.000 moet doen
Het antwoordenboek zegt dit:
[ code verwijderd ]
Maar wat ik ook doe, ik kom niet uit op ¤ 564,43Wie heeft het verlossende antwoord?
¤ 10.000 + p * 13,41675982 = ¤ 50.000 * 0,351457202
wordt
¤ 10.000 + p * 13,41675982 = 17572,....
wordt
p * 13,41675982 = 7572,....
en nu bijde kanten delen door 13,41.....
begrijpelijk ?
(vat dit niet persoonlijk op maar kon je dit nou echt niet


Wow, zo'n applet zoek ik al een tijdje. Thx.quote:
Zijn er ook applets waarmee je leert ingewikkelde stellingen te bewijzen?
There is but one straight course, and that is to seek truth and pursue it steadily. - George Washington
*** Wiskunde Meisjes Blog *** CFR.org *** NRC.nl ***
*** Wiskunde Meisjes Blog *** CFR.org *** NRC.nl ***


Het ging om een algemeen bewijs, niet om een specifieke situatie.quote:Op maandag 30 maart 2009 16:56 schreef Yannick3211 het volgende:
Met die ruit en de diagonalen, heb ik gewoon zo:
[ afbeelding ]
Maar toch bedankt
kloep kloep


Ik ken ze niet, maar als je de naam van de stelling kent, kun je natuurlijk altijd googlen op applet en de naam van de stelling. Zo'n applet lijkt me namelijk alleen werken voor die specifieke stelling.quote:Op maandag 30 maart 2009 17:38 schreef Atlanticus het volgende:
[..]
Wow, zo'n applet zoek ik al een tijdje. Thx.
Zijn er ook applets waarmee je leert ingewikkelde stellingen te bewijzen?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Beste fokkers,
Heb morgen een proefwerk wiskunde over Kwadratische verbanden. En heb even een vraagje;
Hoe kun je de as van symetrie en de top uit deze formule halen;
Y= -x² + x + 6
Ik ben geen topper dus het liefst in simpele stappen uitgelegd!
Heb morgen een proefwerk wiskunde over Kwadratische verbanden. En heb even een vraagje;
Hoe kun je de as van symetrie en de top uit deze formule halen;
Y= -x² + x + 6
Ik ben geen topper dus het liefst in simpele stappen uitgelegd!


Ik heb dit nooit gehad dus voor mij is het gewoon nieuwquote:Op maandag 30 maart 2009 00:41 schreef TubewayDigital het volgende:
[..]
¤ 10.000 + p * 13,41675982 = ¤ 50.000 * 0,351457202
wordt
¤ 10.000 + p * 13,41675982 = 17572,....
wordt
p * 13,41675982 = 7572,....
en nu bijde kanten delen door 13,41.....
begrijpelijk ?
(vat dit niet persoonlijk op maar kon je dit nou echt niet, dit is zo elementair)
Verily i say unto you; dost thou even hoist, brethren? - Jesus (Psalm 22)


je zoekt voor de top de twee 0puntenquote:Op maandag 30 maart 2009 20:40 schreef Jelmer1994 het volgende:
Beste fokkers,
Heb morgen een proefwerk wiskunde over Kwadratische verbanden. En heb even een vraagje;
Hoe kun je de as van symetrie en de top uit deze formule halen;
Y= -x² + x + 6
Ik ben geen topper dus het liefst in simpele stappen uitgelegd!
-x^2+x+6=0
x^2-x-6=0
productsom:
b=-1
c=-6
pq=-6
p+q=-1
p=2
q=-3
(x+2)(x-3)=0
x=-2 v x=3
het gemiddelde van deze 2:
(-2+3)/2=1/2
dus de x-coordinaat is 1/2
invullen geeft ycoordinaat:
y=-x^2+x+6 --> y=-(1/2)^2+1/2+6=6,25
dus de coordinaten van de top zijn (1/2;6,25)
en de symmetrieas is dus de xcoordinaat van de top, dus x=1/2


kon je de top niet gewoon uitrekenen met een klein gedeelte van de abc-formule: -b/4ac?? (tis voor mij ook weer lang geleden)
I never think of the future - it comes soon enough. - Albert Einstein


-b/(2a) inderdaad, staat ook op de pagina die ik gaf.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


nou... ik doe bewegingswetenschappen maar van jou verhaal snapte ik geen moer van....
I never think of the future - it comes soon enough. - Albert Einstein


Je kunt jouw formule Y= -x² + x + 6
ook algemeen schrijven als y=ax2 +bx +c
a altijd voor het kwadraat, b voor de x en de c een getal.
in jouw formule geldt dan a=-1 b=1 en c=6.
De top van een parabool ligt altijd op de symmetrie as. Die is gelijk aan -b/2a.
dus bij jouw parabool 1/2=0,5.
nu x=0.5 in de formule invullen geeft y=6,25.
dan top (0,5 ; 6,25).
ook algemeen schrijven als y=ax2 +bx +c
a altijd voor het kwadraat, b voor de x en de c een getal.
in jouw formule geldt dan a=-1 b=1 en c=6.
De top van een parabool ligt altijd op de symmetrie as. Die is gelijk aan -b/2a.
dus bij jouw parabool 1/2=0,5.
nu x=0.5 in de formule invullen geeft y=6,25.
dan top (0,5 ; 6,25).
kloep kloep


x2ex + ex2x = xex(x + 2).quote:Op woensdag 1 april 2009 03:59 schreef nickybol het volgende:
Hoe ontbind je x^2e^x + e^x2x in factoren?


Weer een vraagje van mij
Het gaat hier om vraag b
Nu weet ik dat het antwoord moet zijn ||b-Ax|| (x= x met dakje)
Ax kan ik berekenen en Ax(dakje) = b(dakje)
Maar dan zou b-Ax toch gewoon (1/6)*[-3-,6,-1]T moeten zijn? (1-4,1-7,0-1)
Wat doe ik fout?
Het gaat hier om vraag b
Nu weet ik dat het antwoord moet zijn ||b-Ax|| (x= x met dakje)
Ax kan ik berekenen en Ax(dakje) = b(dakje)
Maar dan zou b-Ax toch gewoon (1/6)*[-3-,6,-1]T moeten zijn? (1-4,1-7,0-1)
Wat doe ik fout?
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


Geen wiskundegoeroes aanwezig vandaag? 
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


(1-4,1-7,0-1) is fout. Je rekent met helen en zesden door elkaar. De eerste coordinaat is bv. 1-4/6.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


quote:Op woensdag 1 april 2009 17:32 schreef GlowMouse het volgende:
(1-4,1-7,0-1) is fout. Je rekent met helen en zesden door elkaar. De eerste coordinaat is bv. 1-4/6.
Bedankt
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


Nog iets wat ik niet begrijp
Nu snap ik wel dat w1*x = 0 en dat w2*x = 0
Maar waarom is w1 w1 en w2 w2?
Hoe bepaal je dat?
Wat daarna komt snap ik wel, maar hoe bepaal je die basis?
Nu snap ik wel dat w1*x = 0 en dat w2*x = 0
Maar waarom is w1 w1 en w2 w2?
Hoe bepaal je dat?
Wat daarna komt snap ik wel, maar hoe bepaal je die basis?
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


De initiële w1 en w2 kun je gewoon twee willekeurige vectoren voor pakken. Kies twee plekken vast en de derde volgt uit x1+3x2-x3=0.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


ja maar stel ik had w2 als w1 genomen. Had ik dan hetzelfde antwoord gekregen? Al dan niet in meervoud natuurlijkquote:Op woensdag 1 april 2009 21:43 schreef GlowMouse het volgende:
De initiële w1 en w2 kun je gewoon twee willekeurige vectoren voor pakken. Kies twee plekken vast en de derde volgt uit x1+3x2-x3=0.
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,


Nee, een orthogonale basis is niet uniek. Maar je ziet dat je een tweedimensionale ruimte moet krijgen (driedimensionale ruimte met één lineaire restrictie), dus als jij twee orthogonale vectoren hebt die in de ruimte zitten dan ben je klaar.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik heb een kansberekeningsvraagstuk, ik ben zelf niet zo'n wiskunde expert, en kom er niet uit.
Stel je hebt een zak met 100 knikkers, er zitten 5 verschillende kleuren in de zak en van iedere kleur 20. Hoeveel keer moet je trekken om minstens 4 verschillend gekleurde knikkers te verkrijgen? (je trekt zonder terugleggen)
Het zou helemaal geweldig zijn als iemand kan uitleggen hoe je dit met de hand en met een GR uitrekent!
alvast superbedankt!
Stel je hebt een zak met 100 knikkers, er zitten 5 verschillende kleuren in de zak en van iedere kleur 20. Hoeveel keer moet je trekken om minstens 4 verschillend gekleurde knikkers te verkrijgen? (je trekt zonder terugleggen)
Het zou helemaal geweldig zijn als iemand kan uitleggen hoe je dit met de hand en met een GR uitrekent!
alvast superbedankt!
`either you or your head must be off, and that in about half no time! Take your choice!'


om te beginnen heeft het niks met kansberekening te maken.quote:Op donderdag 2 april 2009 12:17 schreef ALICENOR het volgende:
Ik heb een kansberekeningsvraagstuk, ik ben zelf niet zo'n wiskunde expert, en kom er niet uit.
Stel je hebt een zak met 100 knikkers, er zitten 5 verschillende kleuren in de zak en van iedere kleur 20. Hoeveel keer moet je trekken om minstens 4 verschillend gekleurde knikkers te verkrijgen? (je trekt zonder terugleggen)
Het zou helemaal geweldig zijn als iemand kan uitleggen hoe je dit met de hand en met een GR uitrekent!
alvast superbedankt!
Je moet 61 keer trekken wil je er zeker van zijn dat je minstens 4 verschillende kleuren hebt. Worst case scenario: 20 keer rood trekken, daarna 20 keer blauw trekken, daarna 20 keer groen trekken. Dan zijn rood, blauw groen op en elke volgende knikker die je trekt geeft je 4e gezochte kleur. Je kan dus maximaal 60 keer trekken waarbij je 3 kleuren trekt. De 61 keer geeft die 4e kleur.
hoe je dit met de GR doet weet ik niet


En als ik het nou zou stellen: wat is de kans dat je in 10 keer trekken minstens vier verschillende kleuren eruit haalt?
`either you or your head must be off, and that in about half no time! Take your choice!'


Dan zoek je alle mogelijke trekkingen die daaraan voldoen, en tel je de kansen op die trekkingen op. Dat opsommen is hier een monnikenwerk.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Das waar, ik dacht dat met de nCr functie van de GR mss wel iets mogelijk is. Die functie kan toch al de mogelijke combinaties aangeven? Of is dat alleen bij een binomiale verdeling?
`either you or your head must be off, and that in about half no time! Take your choice!'


Dat is inderdaad alleen bij terugleggen en waarbij je bij elke trekking dezelfde kans op succes hebt. Hier kun je niet van een succes spreken.quote:Op donderdag 2 april 2009 14:20 schreef ALICENOR het volgende:
Das waar, ik dacht dat met de nCr functie van de GR mss wel iets mogelijk is. Die functie kan toch al de mogelijke combinaties aangeven? Of is dat alleen bij een binomiale verdeling?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


onder voorbehoud zeg ik 34.1%.
Wat ik zou doen is de kans uitrekenen dat je met 10 keer trekken hoogstens 3 verschillende kleuren trekt.
je hebt namelijk
P(hoogstens 3 verschillende kleuren) + P(minstens 4 verschillende kleuren) = 1
Hoe kom je aan deze opgave? Dit is geen VWO stuff, iig niet met mijn oplossingsmethode
[ Bericht 42% gewijzigd door TubewayDigital op 02-04-2009 20:07:11 ]
Wat ik zou doen is de kans uitrekenen dat je met 10 keer trekken hoogstens 3 verschillende kleuren trekt.
je hebt namelijk
P(hoogstens 3 verschillende kleuren) + P(minstens 4 verschillende kleuren) = 1
Hoe kom je aan deze opgave? Dit is geen VWO stuff, iig niet met mijn oplossingsmethode
[ Bericht 42% gewijzigd door TubewayDigital op 02-04-2009 20:07:11 ]


Ik kom hierop:
- is fout -
[ Bericht 68% gewijzigd door GlowMouse op 02-04-2009 21:31:44 ]
- is fout -
[ Bericht 68% gewijzigd door GlowMouse op 02-04-2009 21:31:44 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hoe ik kom aan deze opgave, haha...
Eigenlijk gaat het om cellen in een fles. Ik loop stage op een lab, en ben bezig met celkweek. Ik heb nu een fles met ongeveer 90 verschillende celsoorten (microscopisch niet te onderscheiden maar genetisch anders) per celsoort heb ik ongeveer 65000 cellen, en dus in totaal ongeveer 6 miljoen. Nou wil mijn begeleider graag weten hoeveel kans je hebt om 10 verschillende soorten cellen te verkrijgen als je ongeveer 500 cellen eruit haalt. Dus ik heb geprobeerd het vraagstuk wat te versimpelen, aangezien het hier om erg grote aantallen gaat. Maar zelf weet ik het ook niet meer....
Vandaar...
Eigenlijk gaat het om cellen in een fles. Ik loop stage op een lab, en ben bezig met celkweek. Ik heb nu een fles met ongeveer 90 verschillende celsoorten (microscopisch niet te onderscheiden maar genetisch anders) per celsoort heb ik ongeveer 65000 cellen, en dus in totaal ongeveer 6 miljoen. Nou wil mijn begeleider graag weten hoeveel kans je hebt om 10 verschillende soorten cellen te verkrijgen als je ongeveer 500 cellen eruit haalt. Dus ik heb geprobeerd het vraagstuk wat te versimpelen, aangezien het hier om erg grote aantallen gaat. Maar zelf weet ik het ook niet meer....
Vandaar...
`either you or your head must be off, and that in about half no time! Take your choice!'


Dat zijn enorme getallen, dat zul je niet zomaar kunnen berekenen. Ik kan je wel een kans geven die ik heb bepaald mbv simulatie, dat geeft een aardige schatting.
Kans op tenminste 10 verschillende soorten bij steekproefgrootte 10 is al 0.6.
Kans op tenminste 10 verschillende soorten bij steekproefgrootte 11 is al 0.9.
Kans op tenminste 10 verschillende soorten bij steekproefgrootte 20 is al nagenoeg 1 (minder dan 10 soorten zal bij minder dan 1 op de miljoen steekproeven voorkomen)
Dus met steekproefgrootte 500 zit je wel veilig.
Kans op tenminste 10 verschillende soorten bij steekproefgrootte 10 is al 0.6.
Kans op tenminste 10 verschillende soorten bij steekproefgrootte 11 is al 0.9.
Kans op tenminste 10 verschillende soorten bij steekproefgrootte 20 is al nagenoeg 1 (minder dan 10 soorten zal bij minder dan 1 op de miljoen steekproeven voorkomen)
Dus met steekproefgrootte 500 zit je wel veilig.
| 1 2 3 4 5 6 7 8 9 10 11 12 | x=0; for i = 1:1000000 r = randint(11,1,[1 90*65000]); r = ceil(r/65000); r = unique(r); if(size(r,1) >= 10) x=x+1; end n=n+1; end x/n |
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Glowmouse, ik weet dat jij ook econometrie studeert dus ik hoop dat je mij verder kan helpen met het uitrekenen van de core van een economie, ik kom er namelijk niet uit, het is tijdens de hoorcolleges een week of drie terug behandeld, maar het staat niet tussen mijn aantekeningen dus kan jij het me misschien uitleggen? Want in het boek kan ik het niet terugvinden.
ff wachten nog


Ik wil er wel even over nadenken, u is de nutsfunctie en e is een nash evenwicht?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


is een endowment, de startsituatie waarmee de 2 handelaren in deze ruileconomie beginnen, de definitie van de core is het punt waarbij er minimaal 1 beter af is, zonder dat de andere erop achteruit gaat
ff wachten nog


Ik zit ernaar te kijken, maar is het niet vreemd dat de startsituatie niet in de core zit?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Met jouw definitie, en x1 x en x2 y noemend (wie verzint dat met zowel super- als subscript), moet je gewoon vergelijkingen oplossen.
Ik kom dan op x2 >= 3/x1 (vanwege speler 1)
en x2 <= 4-3/(4-x1)³ (vanwege speler 2)
Ik kom dan op x2 >= 3/x1 (vanwege speler 1)
en x2 <= 4-3/(4-x1)³ (vanwege speler 2)
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Zo zat ik ook te denken ja, maar dan heb je niet de oplossing van de slide te pakken...quote:Op donderdag 2 april 2009 23:13 schreef GlowMouse het volgende:
Met jouw definitie, en x1 x en x2 y noemend (wie verzint dat met zowel super- als subscript), moet je gewoon vergelijkingen oplossen.
Ik kom dan op x2 >= 3/x1 (vanwege speler 1)
en x2 <= 4-3/(4-x1)³ (vanwege speler 2)
En die scripts zijn absurd ja, ik ben blij als ik van dit vak af ben.
Helaas volgt ook nog wiskundige economie B
ff wachten nog


Nee, toen ik erover nadacht al en toen pas ben ik de simulatie gaan doen. Wat er gebeurde in mijn berekening is dat er heel veel dubbel werd geteld (in het stukje achter de 1-), zodat de kans nog groter zou zijn.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Weet iemand hoe ik in standaardvorm moet opschrijven?
alvast bedankt!
[ Bericht 45% gewijzigd door motorbloempje op 01-09-2013 20:48:18 ]
alvast bedankt!
[ Bericht 45% gewijzigd door motorbloempje op 01-09-2013 20:48:18 ]


Wortel 3/wortel 6 * wortel 3 /wortel 6 * wortel 3/wortel 6 = 3wortel3 / 6wortel6?
Volgens mij is het (1/4)*wortel2, maar hoe ik daar op kom weet ik ook niet
(wortel 3/wortel6)^3 = ((wortel3/wortel6)*(wortel3/wortel3))^3=(3/wortel18)^3=(3/wortel18)*(3/wortel18)*(3/wortel18)=??
[ Bericht 26% gewijzigd door hello_moto1992 op 03-04-2009 15:28:16 ]
Volgens mij is het (1/4)*wortel2, maar hoe ik daar op kom weet ik ook niet
(wortel 3/wortel6)^3 = ((wortel3/wortel6)*(wortel3/wortel3))^3=(3/wortel18)^3=(3/wortel18)*(3/wortel18)*(3/wortel18)=??
[ Bericht 26% gewijzigd door hello_moto1992 op 03-04-2009 15:28:16 ]


-
[ Bericht 100% gewijzigd door motorbloempje op 01-09-2013 20:48:33 ]
[ Bericht 100% gewijzigd door motorbloempje op 01-09-2013 20:48:33 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


maar zowel boven de streep als onder de streep wordt dubbel geteld. Heft dat elkaar niet op?quote:Op vrijdag 3 april 2009 14:20 schreef GlowMouse het volgende:
Nee, toen ik erover nadacht al en toen pas ben ik de simulatie gaan doen. Wat er gebeurde in mijn berekening is dat er heel veel dubbel werd geteld (in het stukje achter de 1-), zodat de kans nog groter zou zijn.


Ik had nchoosek(5,3)*nchoosek(60,10) in de teller en nchoosek(100,10) in de noemer. In de noemer staat het aantal verzamelingen van 10 elementen die je kunt trekken uit een populatie van 100, daar is niets dubbel geteld. In de teller staat het aantal verzamelingen van 10 elementen die je kunt trekken uit een populatie van 60 maal het aantal manieren om zo'n populatie van 60 te vormen. De deelverzameling waarbij alles van soort 1 is tel je dan 5x.quote:Op vrijdag 3 april 2009 16:18 schreef TubewayDigital het volgende:
[..]
maar zowel boven de streep als onder de streep wordt dubbel geteld. Heft dat elkaar niet op.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


b. Stel p > q, kijk eens naar f(q + (p-q)/2)
c. Kijk eens naar f(p + (q-p)/2)
d. Geen nulpunt, dus p=q (volgt uit c). Stel nu dat f wel continu is in p, dan geldt f(p) = lim(x->p) f(x). We weten dus dat de limiet bestaat, en gelijk is aan lim(x->p-) f(x) (limiet met x komt van links). Wat kunnen we zeggen over die limiet en dus over f(p)? Doe nu hetzelfde voor x van rechts (gebruik dat p=q), en kijk wat je dan kunt zeggen over f(p).
[ Bericht 18% gewijzigd door GlowMouse op 04-04-2009 19:00:15 ]
c. Kijk eens naar f(p + (q-p)/2)
d. Geen nulpunt, dus p=q (volgt uit c). Stel nu dat f wel continu is in p, dan geldt f(p) = lim(x->p) f(x). We weten dus dat de limiet bestaat, en gelijk is aan lim(x->p-) f(x) (limiet met x komt van links). Wat kunnen we zeggen over die limiet en dus over f(p)? Doe nu hetzelfde voor x van rechts (gebruik dat p=q), en kijk wat je dan kunt zeggen over f(p).
[ Bericht 18% gewijzigd door GlowMouse op 04-04-2009 19:00:15 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


John heeft van zijn moeder 3800 dollar geleend. Hij spreekt met haar af dat hij elke maand iets zal terugbetalen. De eerste maand betaalt hij 10 dollar terug en daarna elke maand 8 dollar meer dan de vorige maand.
1) Na hoeveel maanden heeft Maurits het bedrag van 3800 dollar afgelost?
Un = 2 + 8n (want Un = U1 + (n-1) . v)
Sn = 0,5 . n . (10 + 2 + 8n)
y1 = Sn
y2 = 3800
calc > intersect geeft (30,08 ; 3800)
Dus: antwoord is na 31 maanden.
Tot zover lukte het wel, maar nu komt de volgende:
2) Hoeveel dollar had John elke maand meer moeten betalen dan de voorgaande maand opdat hij al in 22 weken het bedrag van 3800 dollar had afgelost?
Kan iemand me helpen met vraag 2? Ik zie ff niet hoe ik verder moet. Alvast bedankt!
1) Na hoeveel maanden heeft Maurits het bedrag van 3800 dollar afgelost?
Un = 2 + 8n (want Un = U1 + (n-1) . v)
Sn = 0,5 . n . (10 + 2 + 8n)
y1 = Sn
y2 = 3800
calc > intersect geeft (30,08 ; 3800)
Dus: antwoord is na 31 maanden.
Tot zover lukte het wel, maar nu komt de volgende:
2) Hoeveel dollar had John elke maand meer moeten betalen dan de voorgaande maand opdat hij al in 22 weken het bedrag van 3800 dollar had afgelost?
Kan iemand me helpen met vraag 2? Ik zie ff niet hoe ik verder moet. Alvast bedankt!
Oh really?